涌现动力学如何用来分析复杂系统？ | 新课上线

导语

集智学园联合华侨大学郑志刚教授开设「复杂系统的涌现动力学」系列课程，从同步到集群，从动力系统到统计物理，本课程为你全面、系统地介绍涌现动力学，从物理学视角建立起理论框架。

欢迎感兴趣的研究者加入课程，现在加入可享早鸟价格。

引入

谈起涌现现象，大家不会感到陌生，从鸟群灵活有序的飞行到萤火虫的同步闪烁，从细胞的构成、蛋白质折叠到生命和意识的起源，从液体中原子的结晶、某些金属中电子的超导性到宇宙大爆炸、星系和恒星及行星的形成等。我们总能发现一些无法用部分去推导出整体的现象。

例如成百上千只鸟如何能够协调一致地飞行并迅速躲避捕食者？无生命的分子如何形成有生命的个体？材料在低于某一温度时，电阻会变为零？关于这些问题，我们都无法回到一只鸟、一个分子、一个电子的层面去获得答案。

那么，从科学视角，我们应该怎么去展开涌现问题的研究呢？

目前已经有多种研究路径，包括圣塔菲研究所的复杂自适应理论、Stephen Wolfram的元胞自动机研究、Ilya Prigogine的耗散结构、Per Bak的自组织临界研究、James Crutchfield的计算力学等，除此之外，涌现动力学也是一个重要的理论研究框架。

我们知道，很多涌现问题棘手的原因在于它们分散的动力学特性，海量的组件每时每刻不断地改变它们自身的状态，通过某种方式彼此连接，使我们无法通过检测单独的某个部分来对其进行研究。对这种高维非线性系统的集体行为的动力学分析，就是涌现动力学，它以非线性动力学、统计物理、序参量动力学理论、网络科学等为理论工具，核心是找到各种各样的约化和降维的理论、方法和技术，来探索复杂系统中这些看似不同的现象之间的内在机制、共性和联系。

涌现动力学的研究，推动着理论和工具的创新。例如Arthur Winfree在关于同步现象的研究中，就推动了非线性动力学和统计物理两个学科的融合，非线性动力学主要研究系统随时间演化的复杂方式，而统计力学主要研究原子、分子或其他简单粒子构成的大系统的集体行为，这两个学科可以相互弥补对方的缺陷，一方面，非线性动力学可以轻松处理只有少数变量的小型系统，但它无法处理大粒子群，而这对于统计力学而言只是小儿科；另一方面，统计力学擅长分析达到平衡状态的系统，但它不能处理任何随时间振荡或不断变化的事物，这种融合推动科学研究向前发展迈出了关键一步。这种创新还在不断继续。

涌现动力学既有深刻的数学意义，又能极具信服力地将理论和真实现象联系起来，是研究涌现问题的重要框架。所以，集智学园特别邀请了华侨大学郑志刚教授，开设“复杂系统的涌现动力学”课程，用8节课程，系统性地从动力学到统计物理的基础理论、时域与空域中涌现的研究、到神经动力学中的应用，逐层展开。

课程主题：复杂系统的涌现动力学

课程简介

什么是复杂系统？什么是涌现？
复杂系统涌现行为的机理是什么？
什么是序参量？怎样寻求复杂系统的序参量？
如何建立复杂系统的序参量动力学描述？

复杂系统由大量个体组成，其重要特征是涌现，即在微观层面通过个体间相互作用形成自组织与合作，在宏观层面呈现出各种各样个体所不具备的行为。如果把一个复杂系统比作一个生命有机体的话，科学家的使命就是去感受其生命的脉动，倾听其生命的呼吸，探索其生命的规律和机理。

复杂系统的集体行为表现于不同层次上，涌现则是以群体行为为表现形式、从一个到另一个层面的过渡。复杂系统的涌现会呈现出一些典型的时间与空间行为，其中时间的整体非平衡动态行为在很多情况下是非平庸且可分析的系统行为，其中最简单的动态就是周期振荡，而最简单的协同行为就是同步。

复杂系统集体行为的出现意味着有序的涌现，有序的产生意味着对称破缺的发生，以此形成系统的约束，将系统动力学运动限制在越来越低维的空间中。在状态空间意味着系统自由度和维度的降低，对于状态变量而言则意味着可以用更少的状态变量来对集体行为加以描述，由此孕育了序参量的出现。从理论上来看，这形成了各种各样的约化和降维的理论、方法和技术。

在本系列课程中，我们将同大家一起探索复杂系统丰富多彩的涌现行为及其背后的奥秘，多方位学习了解复杂系统的不同方面的表现，利用动力学方法构建复杂系统的微观叙事，利用统计物理学等方法重构复杂系统的宏观叙事，并利用系统控制等方法构建复杂系统的应用叙事。我们将从涌现的基本物理和数学原理出发，构建涌现动力学的基本理论框架，并将其应用于节律行为、同步、集群、时空斑图、智能与人工智能等热点问题。

课程大纲

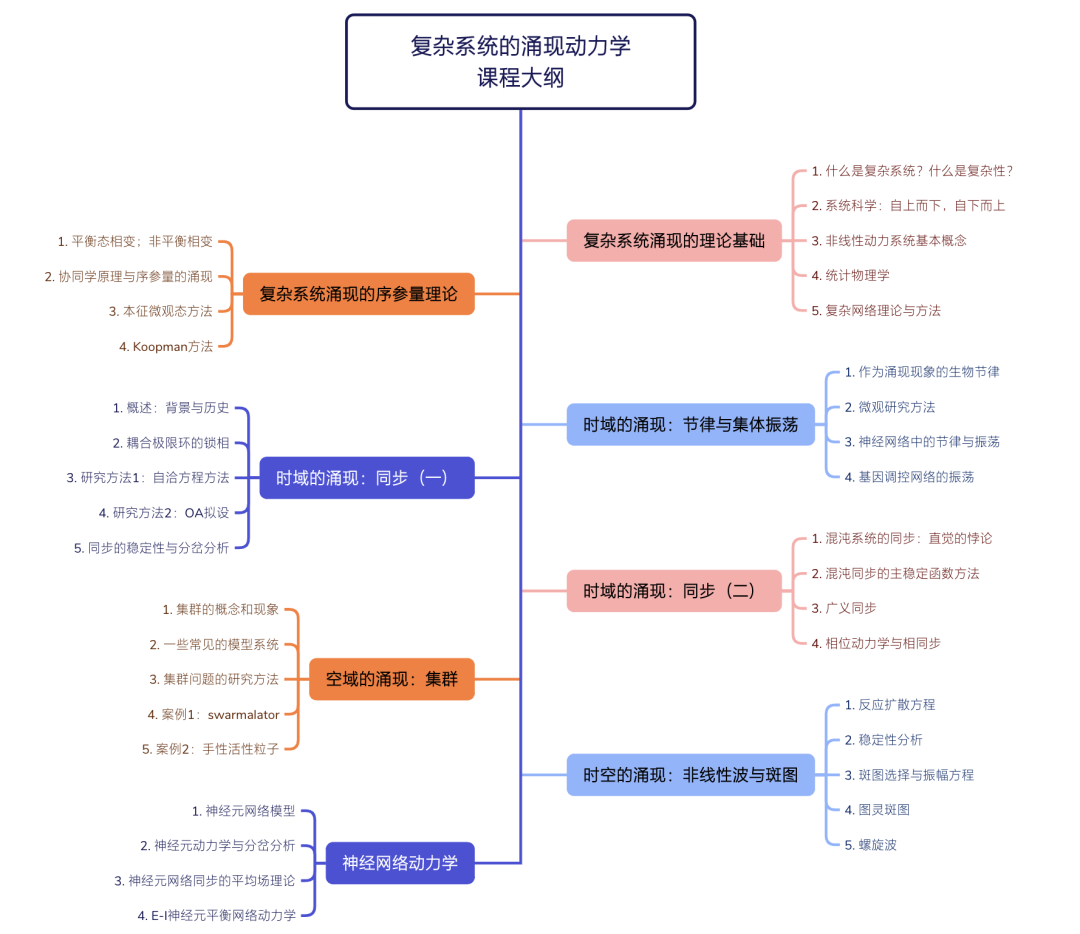
课程主讲人

郑志刚，华侨大学二级教授，研究员-教授双岗，荟萃计划特聘教授，闽江学者、桐江学者特聘教授，福建省百人计划、高层次领军人才，系统科学学科负责人，物理学科带头人。

1997-2015年在北京师范大学工作，2001年破格教授，2006-2011年曾任物理系系主任。2015年至今在华侨大学信息科学与工程学院工作，任华侨大学系统科学研究所所长。曾获全国百篇优博、高校青年教师奖、优秀骨干教师奖等。

目前担任《JAND》杂志副主编，《Chaos》、《Scientific Reports》、《Entropy》、《Chinese Physics B》、《物理学报》等杂志编委。长期从事复杂系统统计物理与非线性动力学方面的教学研究，承担包括973、国家自然科学基金重点项目等国家和省部级项目30多项，在国际刊物发表学术论文200多篇。出版《混沌控制》、《耦合非线性系统的时空动力学与合作行为》、《从动力学到统计物理学》、《复杂系统的涌现动力学》、《生物分子马达的统计物理与复杂输运》等多部专著。

课程详情

第一课：复杂系统涌现的理论基础

本节课程将阐述复杂系统与复杂性的一般特征，讨论如何用系统科学理论和方法开展研究。课程中将介绍：（1）非线性动力系统基本概念，如稳定性，Lyapunov稳定性理论，Lyapunov函数与能量景观，分岔，极限环振荡，混沌等；（2）统计物理学的基本思想和方法，如复杂系统的概率描述、从力学到统计的涌现、系综，态密度演化方程，统计平均，配分函数、相变与临界现象，非平衡与热力学第二定律，非平衡结构的建立等；（3）复杂网络基本思想，复杂系统结构的重构。

1. 什么是复杂系统？什么是复杂性？

2. 系统科学：自上而下，自下而上

3. 非线性动力系统基本概念

4. 统计物理学

5. 复杂网络理论与方法

第二课：复杂系统涌现的序参量理论

本节课程将讨论复杂系统涌现的序参量理论，先通过对于平衡态和非平衡相变研究所得到的对称性破缺和序参量的启示，引出研究复杂系统自组织的协同学基本原理，分析如何从复杂高维系统中得到描述系统行为的序参量，介绍支配原理。对于实际的难以建模的复杂系统，介绍近年来发展的基于复杂时空序列的本征微观态方法和Koopman方法。

1. 平衡态相变；非平衡相变

2. 协同学原理与序参量的涌现

3. 本征微观态方法

4. Koopman方法

第三课：时域的涌现：节律与集体振荡

节律或振荡在生命的世界里无处不在，称为生物钟或生物节律，2017年三位科学家曾因此获诺贝尔生理学或医学奖。

节律是一种涌现吗？是的，它是典型的非线性现象，是各种因素调控、竞争、合作、反馈的自组织结果。

本节课程我们将一起探讨作为时域的一种典型涌现行为来探讨集体振荡的产生机理，并以神经网络和基因调控网络的集体振荡作为研究案例进行分析，引入主超前相位驱动（DPAD）方法和耦合权重方法，揭示涌现并不总是“多者异也”。

1. 作为涌现现象的生物节律

2. 微观研究方法

3. 神经网络中的节律与振荡

4. 基因调控网络的振荡

第四课：时域的涌现：同步（一）

同步是300多年前人们就开始关注的物理现象，而对其的真正理解是从上个世纪后半叶开始。同步是一种典型的节律自组织协同的涌现行为，它联系着很多自组织有序现象。

本节课程从耦合极限环的锁相开始，引入耦合相振子模型如Winfree模型和Kuramoto模型，并讨论在理论上如何分析大量振子的集体同步现象，包括自洽方程方法、Ott-Antonsen ansatz、同步解的稳定性分析等，并将其应用于几个具体案例和应用。

1. 概述：背景与历史

2. 耦合极限环的锁相

3. 研究方法1：自洽方程方法

4. 研究方法2：OA拟设

5. 同步的稳定性与分岔分析

第五课：时域的涌现：同步（二）

混沌系统在动力学上表现出的确定性随机行为来源于其轨道的指数不稳定性，因而很长时间以来人们认为混沌系统之间也是难以产生同步行为的。1990年美国海军实验室Pecora和Carroll的研究表明，这个直觉并不成立。

本节课程将系统介绍混沌系统的同步，包括完全同步，广义同步，相同步等，并探讨复杂网络上的同步动力学。

1. 混沌系统的同步：直觉的悖论

2. 混沌同步的主稳定函数方法

3. 广义同步

4. 相位动力学与相同步

第六课：空域的涌现：集群

集群与协同行为是一种迷人而复杂的现象, 几十年来一直吸引着研究人员的关注。群体行为主要用于描述一群大小相似的个体或动物的空间聚集或在空间迁移时所展现出的集体行为，这是一类典型的复杂系统空间有序行为的涌现。

本次课拟讨论集群行为的微观建模如Reynolds-Boid模型，Couzin-Boid模型，Vicsek模型，Cucker-Smale模型等，流体力学和宏观理论分析，并探讨各种空间集群动力学行为及其转变。

作为案例，课程将剖析手性活性粒子（CAP）和集群振子（Swarmalator）系统的集群动力学行为，并探讨集群动力学在无人机、机器人、集群智能等方面的应用。

1. 集群的概念和现象

2. 一些常见的模型系统

3. 集群问题的研究方法

4. 案例1：swarmalator

5. 案例2：手性活性粒子

第七课：时空的涌现：非线性波与斑图

我们生活的大自然呈现出各种各样的空间结构，不同动物都有自己特定的体表斑纹模式。这些漂亮的结构是怎样形成的？自然界的这些美丽画卷莫非是上帝之手绘就的么？

人们将这些既有时间演化又有空间模式特征的研究对象称为时空斑图。从科学视角来看，斑图(pattern) 可以一般定义为在时间或空间上具有某种规律性的非均匀宏观有序结构。斑图是自然的自组织形式。

本节课程将从微观建模到宏观分析来系统介绍时空结构涌现，引入反应扩散方程和复Ginzburg-Landau方程，探讨斑图选择与振幅方程，开展时空系统的线性稳定性分析，并重点剖析图灵（Turing）斑图、非线性波特别是螺旋波的形成机理与转变。

1. 反应扩散方程

2. 稳定性分析

3. 斑图选择与振幅方程

4. 图灵斑图

5. 螺旋波

第八课：神经网络动力学

大脑是生物体内结构和功能最复杂的组织。大脑是接收外界信号、产生感觉、形成意识、进行逻辑思维、发出指令产生行为的指挥部，掌管人类每天的语言、思维、感觉、情绪、运动等高级活动。构成人脑的神经系统是非线性的动力系统，是一个复杂适应性系统（CAS）。各种高级活动都是大量神经元自组织活动的集体涌现。

本节课程将从耦合神经元网络模型开始，探讨其宏观涌现的机理，特别是关注神经元网络的同步和平衡，构建宏观层面的平均场理论，探讨E-I神经元平衡网络动力学。

1. 神经元网络模型

2. 神经元动力学与分岔分析

3. 神经元网络同步的平均场理论

4. E-I神经元平衡网络动力学

阅读推荐

郑志刚，《复杂系统的涌现动力学–从同步到集体运输（上/下册）》，科学出版社，2019年6月1日

课程适用对象

1. 领域研究者、理工科研究生或高年级本科生：

a. 对非线性动力学、复杂科学、统计物理等领域感兴趣；

b. 具备一定的微分方程、线性代数及计算基础；

c. 对交叉领域研究有热情的研究者；

2. 具有探究精神的学生：

a. 乐于参与讨论、假设推导和问题反思的学生。

报名须知

1. 课程形式：腾讯会议直播，集智学园网站录播。本系列课程不安排免费直播。

2. 课程周期：2025年4月14日-2025年6月16日，每周一晚19点-21点进行。

3. 课程定价：原价799，早鸟价639，早鸟优惠截止到2025年4月14日中午12点。

扫码付费报名课程课程链接：https://campus.swarma.org/course/5482?from=wechat

付费流程：

1. 扫码付费；

2. 课程页面添加学员登记表，添加助教微信入群；

3. 课程可开发票。

课程奖学金机制

1. 途径一：发布高质量课程笔记

在集智斑图网站（pattern.swarma.org）完成本课程体系下某个方向的总结文章或学习路径。经集智学园助教团队评定认可后，可作为一条贡献。一条贡献奖励200元奖学金，质量优异的内容，会有浮动奖励。可参考：

2. 途径二：招募课程助理1名

付费报名课程后，联系助教微信申请课程助理。经沟通，成为正式课程助理，完成课程助理任务，在课程结束后退全额学费。

涌现动力学如何用来分析复杂系统？ | 新课上线