摘要

重整化群是物理学中关于标度、标度不变性和普适性理论的支柱。最近，通过基于扩散动力学，这一工具已被应用于具有成对相互作用的复杂网络。然而，随着复杂系统中多体相互作用的重要性愈发凸显，迫切需要将重整化群方法扩展到高阶网络。在此，我们填补了这一空白，提出了一种适用于任意高阶网络的拉普拉斯重整化群方案。我们方法的核心在于引入跨阶拉普拉斯算子（cross-order Laplacians），它允许描述在任意阶超边上的扩散过程，可以通过任意其他阶的超边发生，对现有的高阶拉普拉斯算子进行了推广。这种方法使我们能够探究高阶结构，定义不同阶的标度不变性，并提出一种粗粒化方案。我们在受控的合成高阶系统上验证了我们的方法，然后将其用于检测来自多个领域的现实世界复杂系统中特定于阶的标度不变性特征的存在。

研究领域：高阶网络，拉普拉斯重整化群，交叉阶拉普拉斯，尺度不变性，复杂系统

 

论文题目：Higher-order Laplacian renormalization
发表时间：2025年2月24日
论文地址：https://doi.org/10.1038/s41567-025-02784-1
期刊名称：Nature Physics
重整化群（RG）是物理学中研究相变与普适性的核心工具。近年来，科学家试图将其推广到复杂网络领域，但传统方法依赖几何嵌入假设，难以描述网络内在的拓扑结构。随着高阶网络（如超图、单纯复形）的兴起，发展针对高阶结构的重整化方法变得迫切，这类网络能描述多节点相互作用，如社交群组、蛋白质复合体。Nature Physics最新研究填补了这一空白，提出高阶拉普拉斯重整化群（LRG），为分析多尺度复杂系统提供了新框架。


交叉阶拉普拉斯算子：高阶扩散的“导航仪”

研究团队的核心创新在于跨阶拉普拉斯算子（cross-order Laplacians）。假设已确认超图Δ具有尺度不变性，怎样能够将其简化为一个更小但等效的超图，但仍能被识别具有尺度不变性呢？沿用网络重整化的思路，研究者设计了一套高阶拉普拉斯重正化方案，包括以下步骤：

1、计算交叉阶拉普拉斯矩阵image.png，该矩阵描述了在k阶超边上通过m阶超边进行的扩散过程。该矩阵是传统拉普拉斯的推广，用于处理更复杂的多元关系。

2、选择一个扩散时间Τ*，它对应于你想要“缩放”并在该特定分辨率下分析网络的尺度。

3、划分k阶超边：通过密度矩阵 ρ(k,m)(Τ*) ，计算k阶超边的划分，使得在扩散过程中强相关的超边被划分到同一组中。

4、超图的粗粒化：通过合并节点粗粒化超图Δ，得到一个新的较小的超图image.png。

5、重复该过程：该过程被迭代进行，每次迭代都会得到一个顶点数量减少或不变的超图序列，整个过程被命名为重正化流。

具体而言，传统网络扩散仅通过边（1-超边）传递信息，而高阶网络中，信息可在不同阶的“超边高速公路”上跳转。例如，三角形（2-超边）可通过共享顶点（0-超边）或嵌套于四面体（3-超边）实现连接（图1a）。该算子通过构建邻接图（adjacency graph），将k阶超边的连接关系映射为加权图节点，权重由m阶超边的共享数量决定。例如，G(1,2) 描述边（1-超边）如何通过三角形（2-超边）相连。这种设计突破了几何限制，使扩散过程能自由穿梭于不同阶结构，形成动态的“拓扑望远镜”。

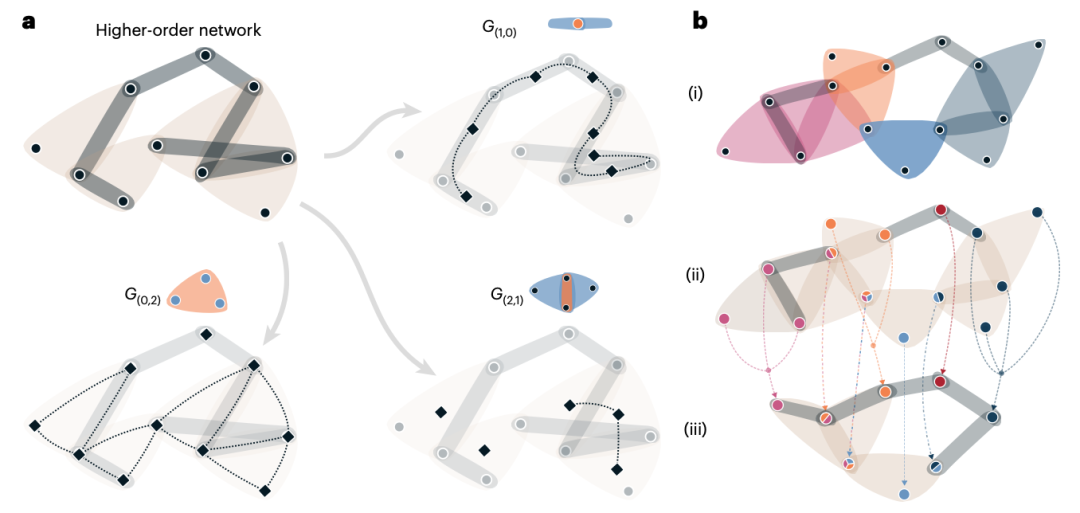
图 1. 跨阶拉普拉斯重整化方案：划分与粗粒化。（a）超图的邻接图构建示意图。注意存在像 G(0,2)  这样的情况，其中边是有权重的（此处用多重边表示）。（b）我们更高阶粗粒化方案的图示表示，k = 2：（i）从 ρ(τ) 获得两个超边的划分，此处用颜色表示；（ii）每个顶点继承一个包含其所属两个超边标签的特征；（iii）具有相同特征的顶点被粘合在一起，超边从起始超图中诱导得出。



熵敏感性曲线：捕捉尺度不变性

研究通过冯·诺依曼熵（von Neumann entropy）量化高阶网络节点或超边之间连接模式的复杂度，计算冯·诺依曼熵对扩散时间Τ*的导数——导数熵敏感性（entropic susceptibility,  C(Τ)）量化高阶结构在不同尺度上的响应性和敏感性。当C(Τ)在时间τ范围内呈现平坦区（plateau），表明系统在该尺度上无特征长度，即尺度不变性。

从下面的伪分形单纯复形可以看到，C(1,2)和C(2,1)曲线展现出跨越多个数量级的振荡平坦区，印证其自相似性；而传统节点-边视角C(0,1)却因小世界效应掩盖了层次结构。这提示我们，高阶结构的尺度特性可能隐藏于特定阶的相互作用中。

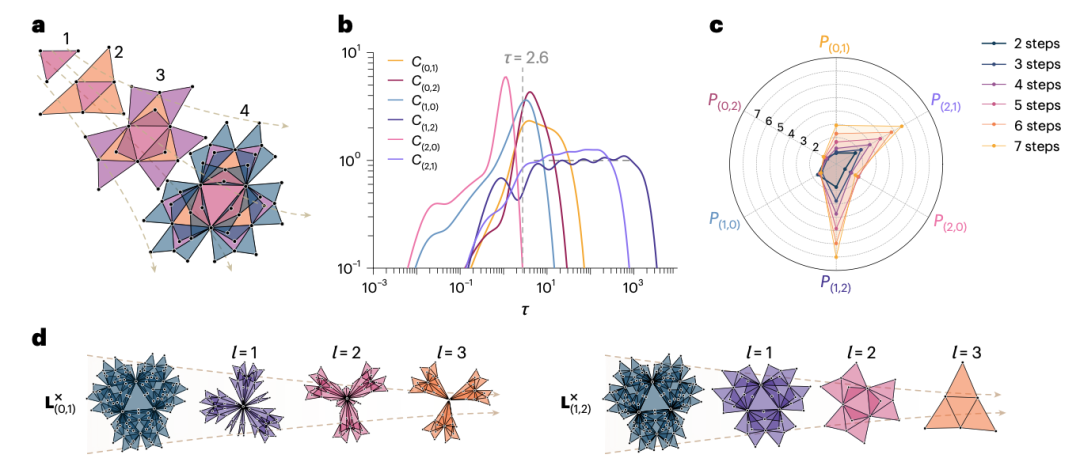
图 2. 伪分形单纯复形中的标度不变性和重整化。(a) 构建具有二维的伪分形单纯形复合体的前三个步骤的图示。(b). 所有跨阶拉普拉斯矩阵的熵敏感性，计算得出的是通过六个步骤构建的二维伪分形单纯形复合体（1,095个顶点）。(c) 随着构建单纯形复合体步骤数的增加，SIP（熵敏感性指数）的变化。(d) 左侧：使用τ* = 0.2的image.png重整化方案的前三个步骤；右侧：使用τ* = 2.6的image.png 重整化方案的前三个步骤。



重整化实战：从合成数据到真实世界

研究通过两类合成模型验证了该方法的有效性。在伪分形模型中，拉普拉斯算子成功逆向其构造过程，将迭代生成的复形逐层坍缩回初始单元（图2d）。NGF模型：相比节点视角image.png的重整化，基于image.png的方法更渐进地保留结构，避免过度坍缩（图3c）。

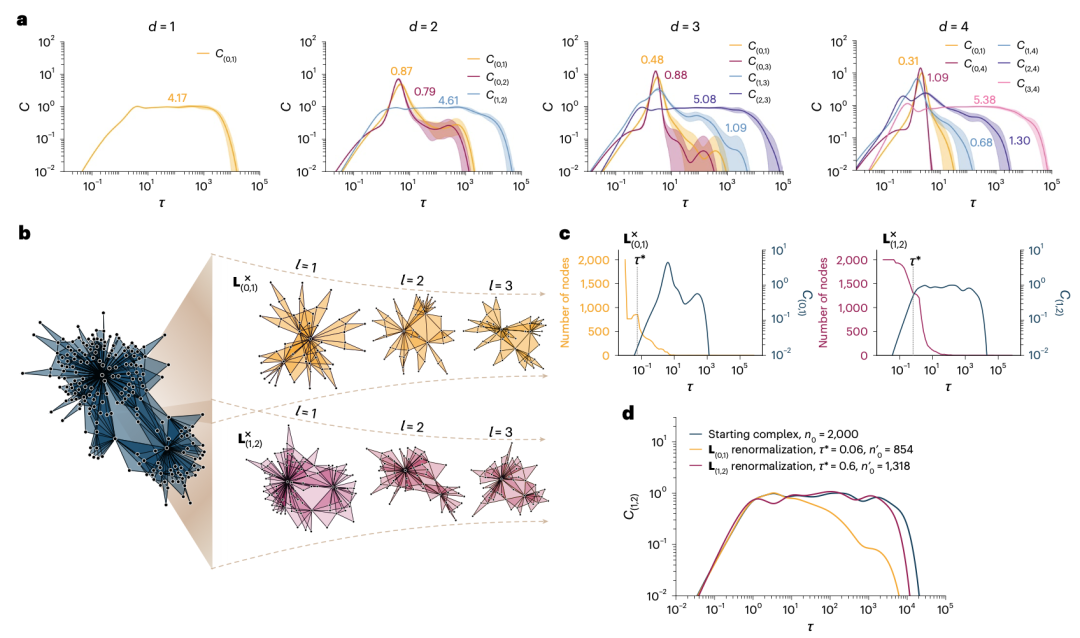
图 3. 应用于 NGF 单纯复形的高阶拉普拉斯重整化方案。（a）NGF单纯形复合体的熵敏感性（SIP）及其在十次重复实验中的95%置信区间，考虑了味道s = 1，维度d ∈ {1, 2, 3, 4}，β = 5，且有3,000个顶点。数字表示SIP值。（b）一个小型二维NGF单纯形复合体使用image.png（上）和L×(1,2)（下）进行重整化。（c） 左侧：C(0,1)与经过一步image.png重整化后的单纯形复合体顶点数量随τ的变化。右侧：C(1,2)与经过一步image.png重整化后的单纯形复合体顶点数量随τ的变化。（d） 在考虑的两种重整化方法后，熵敏感性C(1,2)的演变。起始的NGF单纯形复合体有2,000个顶点，通过image.png（τ* = 0.06）被减少到854个顶点，通过image.png（τ* = 0.6）被减少到1,318个顶点。


进一步将该方法应用于真实数据中（图4），高中社交联系网络（High-school contacts）的熵敏感性呈现花朵状模式，在特定阶数存在尺度不变性，可能与学生间的社交互动、集群性或小组形成有关。而下面的恩隆数据集（Enron email data）则表现出较为均匀的熵敏感性分布，节点间的交互虽然具有复杂性，但整体来看，网络在不同阶数上的尺度特征表现较为平衡。

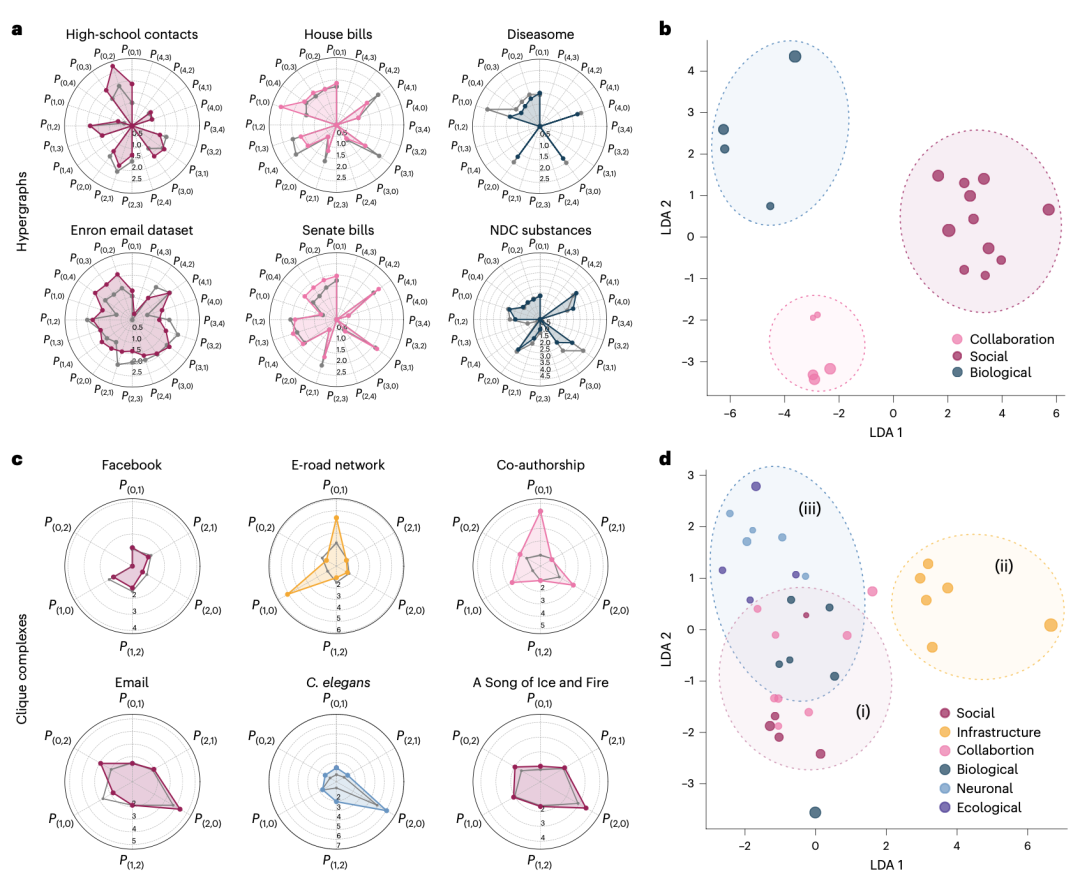
图 4. 真实数据中的高阶尺度不变性。(a) 从真实世界数据集中获得的六个超图（截断至 4 阶）的 P(k,m) 值。这灰色线条及关联区域代表了零模型在十次重复中 P(k,m) 值的平均值和 95% 置信区间。NDC，国家药品代码。(b) 不同类型的 20 个真实超图的LDA投影，用不同颜色表示，其大小与最高 SIP 值成比例。彩色区域突出显示了属于同一类超图的邻近点的簇。c，从真实世界网络数据集中获得的六个二阶团复合体的 SIP 值 P(k,m) 。灰色线条及关联区域代表了零模型在十次重复中 P(k,m) 值的平均值和 95% 置信区间。(d) 34 个不同类型的实际团复合体的 LDA 投影，用不同颜色表示，其大小与网络的最高 SIP 值成比例。彩色区域突出显示了属于同一类的邻近点簇：社会起源（i）、基础设施（ii）和生物起源（iii）。



意义与展望

这项研究首次将重整化群系统推广到任意高阶网络，其价值体现在：在理论层面突破，提供跨阶结构的统一分析框架，超越传统Hodge拉普拉斯算子的局限性。有很强的应用潜力，为社交传播、脑网络分析等领域揭示多尺度机制的阶特异性，例如疾病防控可针对特定阶结构设计干预策略。未来，结合多阶算子组合与机器学习，或能进一步解码复杂系统中“低秩潜在结构”，推动网络科学迈向更高维度。

彭晨 | 编译

高阶网络社区


随着对现实世界探索的不断深入，人们发现在许多真实的复杂系统中，组成系统的个体之间不仅存在二元交互关系，也广泛存在多个体同时（或以特定顺序）进行交互，即高阶交互现象。为此，研究人员分别发展出了基于超图、单纯复形、依赖关系等的网络高阶表示模型，为复杂网络分析和研究提供了新的思路。

由电子科技大学吕琳媛老师、任晓龙老师及中国地质大学（北京）管青老师在集智俱乐部联合发起了【高阶网络读书会】。读书会围绕高阶交互网络的基本概念、模型、方法与应用等研究进行研讨，按照「基础理论」+「深入理论」+「案例研讨」的模式展开。读书会第一季已经圆满结束，第二季正在筹备中。现在报名加入可以解锁第一季全部录播视频并加入社群交流。

图片

详情请见：

探索复杂系统高阶交互的奥秘 | 高阶网络读书会启动

推荐阅读
1. Nat. Rev. Phys.速递：高阶网络上的传染动力学
2. 拓扑深度学习捕捉数据的高阶关系：信息传递拓扑神经网络概述
3. Nat. Phys.速递：异构网络的拉普拉斯重整化群
4. 张江：第三代人工智能技术基础——从可微分编程到因果推理 | 集智学园全新课程
5. 解锁集智全站内容，开启新年学习计划

6. 加入集智，一起复杂！


点击“阅读原文”，报名读书会