高阶网络捕捉了复杂系统中存在的多体相互作用,揭示了拓扑结构与动态之间的相互作用。高阶拓扑动力学理论将高阶相互作用与离散拓扑和非线性动力学结合起来,有望加深我们对复杂系统(如大脑和气候)的理解,并推动下一代人工智能算法的发展。该理论框架超越了传统的节点中心描述,通过拓扑信号来编码网络的动态——这些信号不仅分配给节点,还分配给边、三角形和其他高阶单元。最新的研究结果表明,拓扑信号导致了不同类型的动力学状态和集体现象的涌现,包括拓扑同步、Dirac同步、模式形成和三元渗流等。这些结果提供了对拓扑如何塑造动态、动态如何学习拓扑以及拓扑如何动态演化的洞见。本文旨在指导物理学家、数学家、计算机科学家和网络科学家了解新兴的高阶拓扑动力学领域,并概述未来的研究挑战。
研究领域:高阶网络,拓扑信号,同步,狄拉克算子,渗流
论文题目:Topology shapes dynamics of higher-order networks
论文地址:https://www.nature.com/articles/s41567-024-02757-w
从大脑神经元到气候系统,复杂系统的行为往往源于多体相互作用,而传统网络科学仅能描述成对连接。近年来,高阶网络(Higher-order networks)通过引入三角形、四面体等结构,揭示了多体相互作用如何与拓扑耦合,催生了“高阶拓扑动力学”这一新兴领域。这一理论将拓扑信号(变量不仅定义在节点,还附着于边、三角形等高维结构)与非线性动力学结合,为理解脑功能、气候振荡甚至设计新一代AI算法提供了全新视角。
传统网络将复杂系统简化为节点与连边的集合,却忽视了真实的“群体互动”——比如三个神经元同时激活形成的三角回路,或社交网络中三人成组的传播效应。高阶网络通过引入“单纯复形”(Simplicial Complexes)结构,将三角形、四面体等作为基本单元,更精准地刻画多体相互作用。例如,大脑功能网络的拓扑数据分析发现,高阶空洞(Holes)与信息传递效率直接相关。
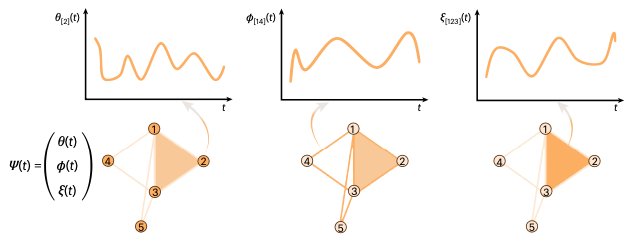
拓扑信号(Topological signals)的提出进一步改变了动力学框架:网络的动态状态不再局限于节点变量,边上的信息流(如神经元突触信号)、三角形上的协同振荡(如气候系统中的洋流循环)均被纳入统一模型——“拓扑旋量”(Topological Spinor)。这种高维视角为动力学赋予了“几何直觉”,例如,边信号的同步可能沿着网络中的环状结构传播。
图 1. 高阶网络的动态状态。超越以节点为中心的网络动力学视图,通过拓扑旋量Ψ捕获高阶网络的动态,为每个节点,边缘,三角形和高阶简单体分配动态变量。
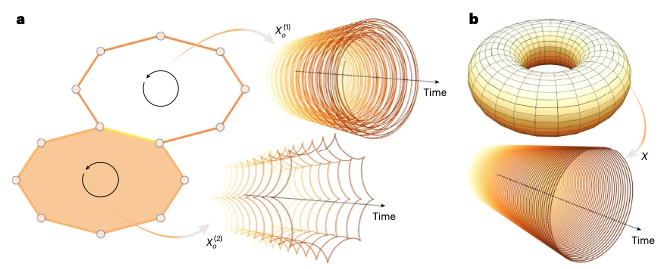
同步现象是复杂系统的标志性行为,例如萤火虫齐闪、心脏起搏等,目前还难以完全解释其机制。研究者将经典的Kuramoto模型扩展为拓扑Kuramoto模型,发现同步能否发生取决于网络的拓扑缺陷:当高阶网络存在“n维空洞”时,对应维度的拓扑信号才能实现同步,且同步态会局域在空洞周围。例如,在一个包含两个环形空洞的脑网络中,边信号的同步可能选择其中一个环振荡,或两者交替主导。
更有趣的是,全局拓扑同步的存在直接受制于网络的调和向量(Harmonic Eigenvectors)。只有当网络结构允许全域一致的信号传播时(如环面网格),高阶同步才能发生。这种“结构决定动力学边界”的特性,为设计可控的振荡网络(如人工神经元阵列)提供了理论依据。
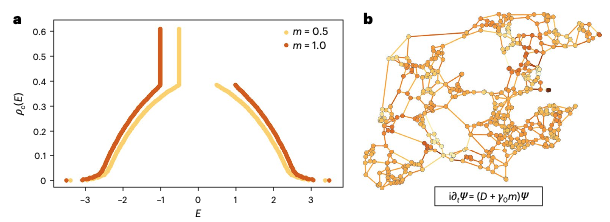
传统方法难以描述不同维度拓扑信号的耦合,而拓扑狄拉克算子(Dirac Operator)成为破局关键。它像一位指挥家,协调节点、边、三角形上的信号协同演化,催生了“狄拉克同步”(Dirac Synchronization)。这种同步不仅呈现非连续相变,还会自发产生节律波动——类似脑电波的α节律或气候系统中的季风振荡。
在模式形成中,狄拉克算子揭示了静态与动态拓扑图灵斑图的差异:仅当节点与边信号通过狄拉克耦合时,才会涌现动态斑图(如气候系统中的混沌振荡)。这种跨维度的动力学对话,为理解生物节律和设计物理启发的AI算法开辟了新路径。
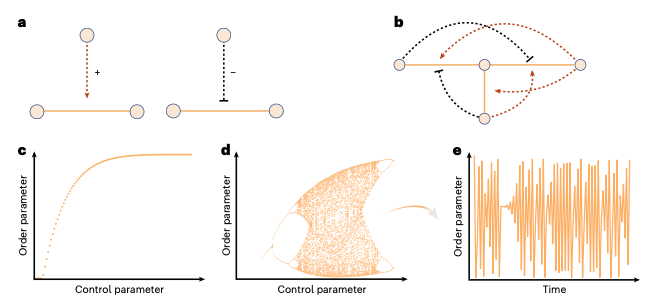
现实网络的拓扑并非静止。研究者提出三元渗流(Triadic Percolation)模型,探索“节点如何调控连边”的反哺机制。例如,社交网络中某人可增强或抑制他人的联系,导致巨连通分量(Giant Component)随时间混沌涨落。这种动态相变与logistic映射同属一个普适类,甚至可模拟大脑静息态网络的“闪烁”连接模式。
在空间网络中,三元渗流会引发时空交替的拓扑模式——如同气候系统中厄尔尼诺与拉尼娜的切换。这种“拓扑-动力学共进化”的框架,为预测脑疾病中的网络重构或极端气候事件提供了新工具。
高阶拓扑动力学仍处于爆发期,如何统一拓扑信号的信息理论、发展高维持久同调算法、构建物理驱动的AI架构,将是关键方向。
彭晨 | 编译
随着对现实世界探索的不断深入,人们发现在许多真实的复杂系统中,组成系统的个体之间不仅存在二元交互关系,也广泛存在多个体同时(或以特定顺序)进行交互,即高阶交互现象。为此,研究人员分别发展出了基于超图、单纯复形、依赖关系等的网络高阶表示模型,为复杂网络分析和研究提供了新的思路。
由电子科技大学吕琳媛老师、任晓龙老师及中国地质大学(北京)管青老师在集智俱乐部联合发起了【高阶网络读书会】。读书会围绕高阶交互网络的基本概念、模型、方法与应用等研究进行研讨,按照「基础理论」+「深入理论」+「案例研讨」的模式展开。读书会第一季已经圆满结束,第二季正在筹备中。现在报名加入可以解锁第一季全部录播视频并加入社群交流。
6. 加入集智,一起复杂!