《AI×SCIENCE十大前沿观察》7:物理世界的第一性原理
导语
上海科学智能研究院、集智科学研究中心和阿里云联合发布了《AI × Science十大前沿观察》,梳理出35个研究前沿,来推动科学发展的黄金时代到来。本篇为前沿观察7,扫描下方二维码,可获得完整版下载地址、快速链接论文原文。

物理世界的第一性原理
物理世界的第一性原理
背景介绍
目前的人工智能领域发展迅猛,展现出强大的能力。然而,这些基于深度学习和大模型的人工智能系统存在一个共同的弱点:它们大多是通过堆积数据和算力的手段构建的,缺乏对人类和自然智能系统本质的深刻洞察。例如,现有人工智能系统能耗巨大,而人类大脑却能以远低于此的能耗完成各种复杂任务。由人类设计的人工智能,和自然演化下的生物智能,包括我们人类的大脑,是否存在统一的运作机制?智能的本质是什么?我们是否能设计出更有效的智能系统?要回答这些问题,我们迫切需要寻找复杂智能系统的第一性原理。
物理学的思想常常被用来指导 AI 模型的构建。2024年诺贝尔物理学奖授予 John Hopfield 和 Geoffrey Hinton,表彰他们“通过人工神经网络实现机器学习的基础性发现和发明”。这两位研究者将统计物理中的经典模型应用于神经网络架构设计,从而大大提升了机器学习问题的求解效率,为人类进入深度学习时代开辟了先河。
统计物理是连接微观与宏观的桥梁,提供了研究物质世界宏观性质的强有力的理论工具。在机器学习中,统计物理的思想常被用来设计处理具有随机性的模型,统计物理学中的许多概念(比如熵、混沌)和一些经典物理模型(比如伊辛模型)常被借鉴到机器学习中。在神经网络领域,基于能量的模型(Energy-Based Models,EBMs)通过引入物理学的能量概念来构建学习框架。这类模型通过最小化系统能量状态的方式进行网络训练,将能量函数与损失函数相关联,从而提升网络性能和泛化能力。典型的应用案例包括受限玻尔兹曼机(RBM)和深度信念网络(DBN),其核心架构正是基于能量模型的原理设计而成。[6] 生成模型(Generative Model)旨在学习数据样本背后的概率分布,并据此随机采样生成新的样本。目前主要的生成模型包括扩散模型、自回归模型、流模型、变分自编码器等。[5]
本部分将从物理的第一性原理和数学的第一性原理两个方面,介绍关于复杂智能系统的第一性原理的三种可能理论方向:
-
自由能原理(Free Energy Principle, FEP)根源于统计物理和热力学,基于自由能原理的主动推理被认为是智能的第一性原理的备选方案,可能成为新时代复杂系统的大统一理论。通过自由能原理,我们可以更深入地理解智能系统如何运作,为未来的人工智能研究和发展提供更加深刻和基础的理论支持;
-
为了展示物理的普适原理如何帮助我们改进AI系统,我们介绍了泊松流模型(Poisson flow generative model,PFGM)这一结合了物理原理和深度学习的生成模型。
-
范畴论(Category theory)被称为是“数学的数学”,为现代数学提供了一套基础语言。范畴论被用来刻画大模型的能力边界,理解智能的本质,并为自我意识提供数学定义。
从物理或数学的第一性原理出发,我们希望站在复杂智能系统的普适视角更好地理解 AI 大模型的工作原理,从而为改进模型以及提高模型的可解释性提供更高维度的洞察。
研究进展
研究进展
进展目录
自由能原理:智能的第一性原理
泊松流模型:物理启发的深度生成模型
范畴论:刻画大模型的能力边界
自由能原理:智能的第一性原理
推荐理由:自由能原理被认为是“自达尔文自然选择理论后最包罗万象的思想”[1],从第一性原理出发解释智能体更新认知、探索和改变世界的机制,被认为有可能成为智能的第一性原理的重要候选方案,并有望成为新时代复杂系统的大统一理论。
生命何以存在?从微小的细菌到复杂的多细胞动物,再到具有高度智能的人类,各种形式智能背后是否存在统一的普适原理?著名理论神经科学家 Karl Friston 提出了自由能原理(Free Energy Principle, FEP),尝试从第一性原理出发解释智能体更新认知、探索和改变世界的机制。自由能原理基于统计物理和热力学,认为任何与环境处于平衡的自组织系统都必须使其自由能最小化,即最小化内部状态与外部环境预期之间的差异。该原理本质上是对自适应系统(即生物智能体,如动物或大脑)如何抵御自然无序趋势的数学表述。基于自由能原理的主动推理(Active Inference)提供了一个建模感知、学习和决策过程的统一框架。[2]
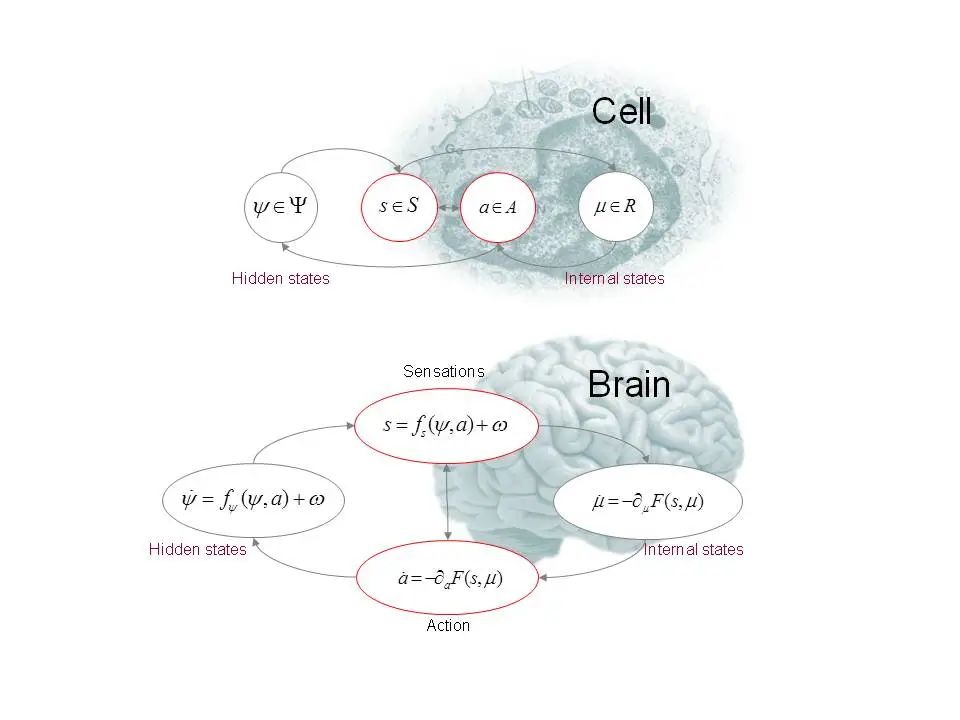
自由能原理尝试从第一性原理出发为生命和智能提供统一的解释 | 来源:Karl Friston
人工智能领域中的强化学习与以自由能原理基础的主动推理框架存在紧密联系。例如在强化学习世界模型中,智能体首先通过观测数据推断隐状态的动力学模型,然后基于学习到的世界模型进行决策规划和探索。在面对复杂环境时,智能体往往需要学习一个多尺度的世界模型。这一发现启示我们,不论是自然演化下的生物智能,还是由人类设计的人工智能,在运作的底层逻辑上或许殊途同归。[3]
Karl Friston 等人在2024年发表的论文 Designing Ecosystems of Intelligence from First Principles 中,展望了未来人工智能的发展愿景,认为人工智能的设计不应局限于模仿大脑,而应该拥抱各式各样的自然智能。在自然界,从粘菌到鱼群再到整个森林,集体智能无处不在,生物体共同协作以适应和生存,人类则通过网络分享想法。然而,大多数 AI 系统无法与人类或其他 AI 共享信息,也无法表达它们如何实现目标。基于此,超级人工智能更可能的形式是智能生态系统的分布式网络,一种可能的实现路径是通过主动推理框架构建集体智能(Collective Intelligence)。[4]
泊松流模型:物理启发的深度生成模型
推荐理由:对物理第一性原理的理解可以反过来帮助我们提出或改进AI算法。作为案例,由基本物理规律启发的深度生成模型,基于热力学的扩散模型[8]和基于静电学的泊松流模型[9],已在高清图像、3D模型、蛋白质结构等生成任务中大放异彩。其中,泊松流模型由集智社区成员许逸伦、刘子鸣等人提出。
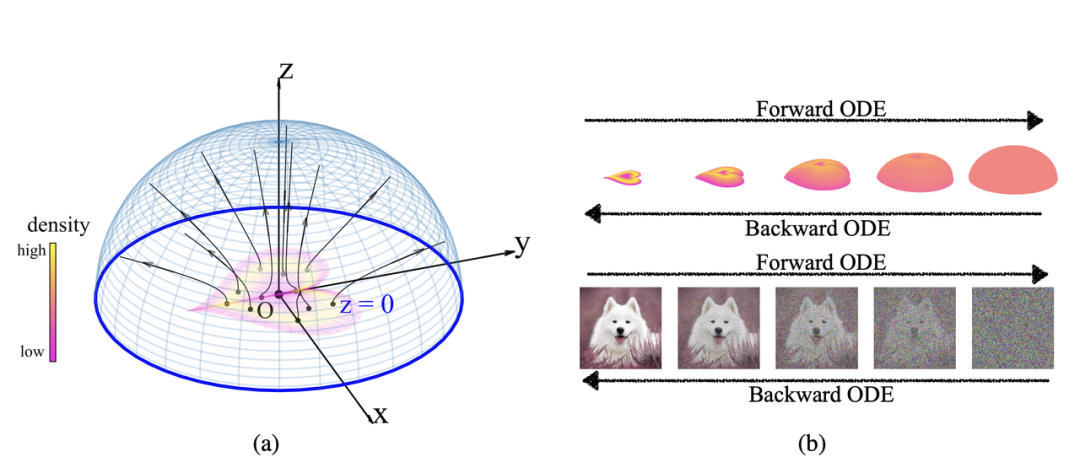
泊松流模型示意图。|来源:Xu, Y., Liu Z. et al (2023). Poisson Flow Generative Models. Neural Information Processing Systems (NeurIPS)
泊松流模型(Poisson flow generative model,PFGM)能够学习数据分布的电场,并使用这个电场来生成新的数据点,从而实现图像生成。具体而言,模型将数据点(例如图像)解释为在 z=0 平面上的正电荷,这些电荷在空间中产生一个高维电场,电场是泊松方程解的梯度,模型通过求解由电场引起的一对正向和反向常微分方程来实现泊松流。相比于扩散模型,泊松流模型更为鲁棒,能够生成同等或更优质量的图像,且速度快10至20倍。泊松流模型利用了电场这种物理结构,这个过程结合了物理原理和深度学习,提供了一种新的视角来理解和改进生成模型。
进一步,物理启发的生成模型还在原子尺度物质结构的生成与设计中展现出巨大的潜力。基于和统计物理的内在联系,生成模型对于优化“大自然的损失函数”——变分自由能具有独特优势,这为求解困难的统计物理和量子多体问题提供了新的可能。同时,物理学的洞察也在推动生成模型的发展和创新。通过借鉴物理学原理和方法,还可以设计出更加高效、更加统一的生成模型,以应对人工智能领域的挑战。[5]
范畴论:刻画大模型的能力边界
推荐理由:大模型的能力边界在哪里?已有的机器学习理论无法回答这个问题,因为这些理论研究的对象在这个问题中不存在了,范畴论可以为此提供一个解答。范畴论被用来刻画大模型的能力边界,理解智能的本质,为自我意识提供数学定义。[10, 11] 本研究工作由集智社区成员、清华大学交叉信息学院袁洋完成。
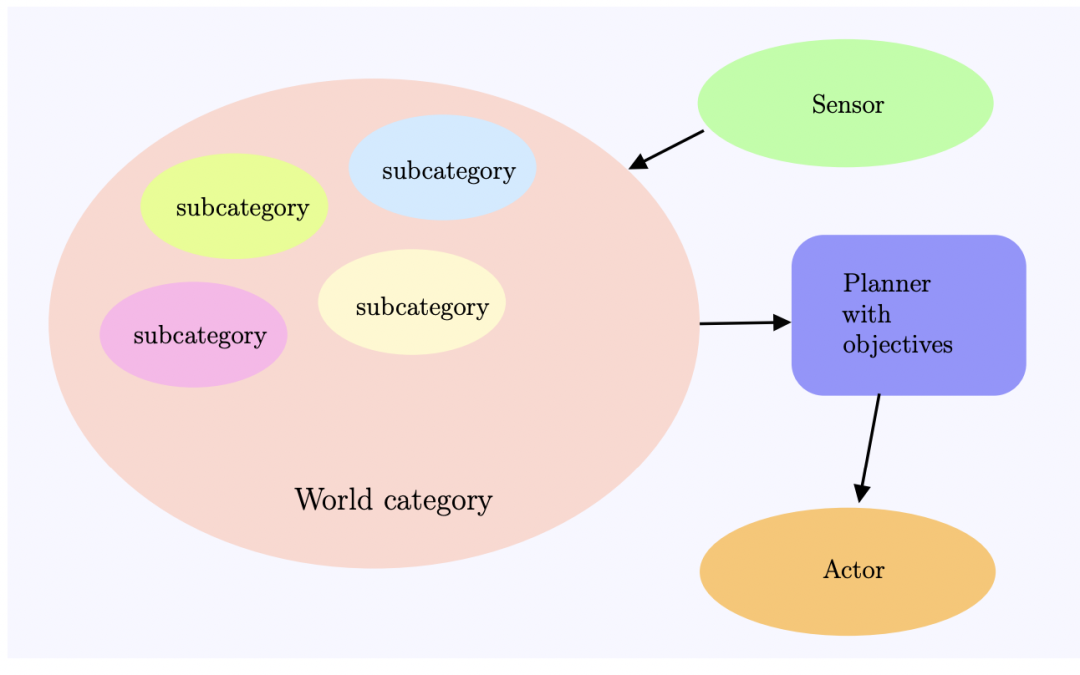
理解智能系统的一种范畴论框架 | 来源:Yuan, Yang. A Categorical Framework of General Intelligence. arXiv preprint arXiv:2303.04571 (2023)
复杂智能系统的第一性原理,也可能包含在最新的数学理论分支之中——范畴论。假如我们有无限的资源,比如有无穷多的数据、无穷大的算力、无穷大的模型、完美的优化算法与泛化表现,由此得到的预训练模型是否可以用来解决一切问题?集智社区成员、清华大学交叉信息学院助理教授袁洋在 On the Power of Foundation Models 这篇论文中,通过范畴论视角,对基础模型的能力进行了理论分析,提出了限制和可能性,并提供了一个用于监督和自监督学习的范畴论框架。[10]
具体而言,范畴论提供了一种鸟瞰视角来理解监督学习。它本身不会替代原有的更具体的监督学习框架,或者用来产生更好的监督学习算法,而是将监督学习框架作为“子模块”。它更关注范畴与函子的结构,并尝试理解某个函子是否可学习。这些问题在传统监督学习框架中极为困难,但是在范畴论视角下变得简单。从机器学习的角度来看,自监督学习也是一种监督学习,只是获取标签的方式更巧妙一些而已。而从范畴论的角度来看,自监督学习定义了范畴内部的结构,监督学习定义了范畴之间的关系。因此,它们处于人工智能地图的不同板块,在做完全不一样的事情。
挑战与展望
挑战与展望
通过自由能原理,我们可以更深入地理解智能系统如何运作,为未来的人工智能研究和发展提供更加深刻和基础的理论支持。例如,人工智能领域中的强化学习与以自由能原理为基础的主动推理框架存在紧密联系。在强化学习领域,新算法的设计大多依赖启发式的想法,缺乏第一性原理,自由能原理则为不同强化学习算法提供了一个统一的视角。[3] 范畴论则有可能帮助我们从数学的角度理解大模型的局限性[10],并有望提炼、表述智能系统的第一性原理。
PNAS 杂志近期发表的“物理学遇见机器学习”(Physics Meets Machine Learning)主题特刊引言指出,统计物理学在人工神经网络发展的初期推动了诸多关键进展,但最近深度学习神经网络追求快速的应用驱动型发展,忽视了理论基础,深度学习的下一个突破可能来自基于统计物理学概念和方法建立的坚实理论基础。[7] 随着更多物理模型被深度挖掘,人工神经网络中何以涌现出复杂智能、深度学习神经网络究竟学到了什么等人工智能谜题将逐渐清晰。
除此之外,通过借鉴量子力学的基本特性,如量子叠加或量子纠缠,人们提出了各种量子AI算法。量子机器学习结合了量子计算的速度和机器学习的学习能力,通过模拟量子力学的基本原理,在处理数据时展现出了传统算法无法比拟的潜力。量子深度学习使用量子计算代替传统的冯·诺依曼机计算,使深度学习算法实现了量子化,达到了显著提高算法并行性和降低计算复杂度的目的。量子演化算法模仿生物进化过程,大大提高了算法的并行性和收敛速度。[6]
拥有大规模参数和复杂网络结构的 AI 大模型是一个典型的复杂系统,展现出一系列复杂系统常见的现象规律,如涌现(Emergence)、标度律(Scaling Law)等。采用复杂科学相关的研究手段,如统计物理、复杂适应系统、复杂网络、非线性动力学、范畴论等工具,有助于我们理解和改进 AI 大模型,从第一性原理出发揭示智能系统底层的统一规律。
参考文献
[1] The Genius Neuroscientist Who Might Hold the Key to True AI
https://www.wired.com/story/karl-friston-free-energy-principle-artificial-intelligence/
|
《连线》杂志的这篇文章主要介绍了神经科学家 Karl Friston 的工作,尤其是自由能原理,这可能是通向真正人工智能的关键。 |
[2] Friston, Karl. The free-energy principle: a unified brain theory?. Nature reviews neuroscience 11.2 (2010): 127-138.
https://www.nature.com/articles/nrn2787
|
该综述从自由能原理视角审视了生物和物理科学中一些重要的大脑理论,包括贝叶斯大脑、预测编码和信息最大化原则、层次推理和注意力理论、神经达尔文主义、信息论和最优控制理论等,表明几种全局性大脑理论可能在自由能框架内得到统一。 |
[3] Mazzaglia, Pietro, et al. The free energy principle for perception and action: A deep learning perspective. Entropy 24.2 (2022): 301.
https://www.mdpi.com/1099-4300/24/2/301
|
这篇论文提供了自由能原理的概述,并从深度学习的角度探讨了感知和行动的自由能原理。论文讨论了深度主动推断主体如何学习环境的生成模型,并与之互动。 |
[4] Friston, Karl J., et al. Designing ecosystems of intelligence from first principles. Collective Intelligence 3.1 (2024): 26339137231222481.
https://journals.sagepub.com/doi/10.1177/26339137231222481
|
文章探讨了如何从第一性原理出发设计智能生态系统,提出使用主动推理作为研究和开发人工智能的一种方法,旨在发展自然和人工智能的生态系统。尽管神经科学是AI研究的关键灵感来源,但我们必须超越大脑,拥抱自然智能的主动和层级特性,这些特性存在于生物体中,也可能在更广泛的物理系统中实现。 |
[5] 写给物理学家的生成模型。王磊,张潘,《物理》2024年第6期。
https://wuli.iphy.ac.cn/article/doi/10.7693/wl20240602
|
文章从物理的视角介绍扩散模型、自回归模型、流模型、变分自编码器等现代生成模型。 |
[6] Jiao, Licheng, et al. AI meets physics: a comprehensive survey. Artificial Intelligence Review 57.9 (2024): 256. https://link.springer.com/article/10.1007/s10462-024-10874-4
|
这篇综述深入探讨了物理学与人工智能发展的相互促进。重点讨论了物理学如何启发 AI 深度学习范式,介绍了物理学的四大领域(经典力学、电磁学、统计物理、量子力学)如何启发现代机器学习模型的构建,并简要介绍了 AI 如何解决物理学问题的相关工作。 |
[7] Levine, Herbert, and Yuhai Tu. Machine learning meets physics: A two-way street. Proceedings of the National Academy of Sciences 121.27 (2024): e2403580121. https://www.pnas.org/doi/10.1073/pnas.2403580121
|
文章关注机器学习领域与物理学之间的双向互动,一方面是机器学习能为物理学做些什么,另一方面则是物理学能为机器学习做些什么。文章认为,人工神经网络受益于统计物理学和神经科学这两个自然科学学科,深度学习的下一个突破可能来自基于统计物理学概念和方法建立的坚实理论基础。 |
[8] Ho, Jonathan, Ajay Jain, and Pieter Abbeel. Denoising diffusion probabilistic models. Advances in neural information processing systems 33 (2020): 6840-6851.
https://proceedings.neurips.cc/paper/2020/hash/4c5bcfec8584af0d967f1ab10179ca4b-Abstract.html
|
本文介绍了去噪扩散概率模型(Denoising Diffusion Probabilistic Model,DDPM)这种生成模型。DDPM 是一种受非平衡热力学启发的潜变量模型,用于高质量图像合成,可以说是 AI 绘画的基石。DDPM 的训练过程包括前向过程(不断加噪声)和反向过程(从噪声生成图像)。 |
[9] Xu, Y., Liu Z. et al (2023). Poisson Flow Generative Models. Neural Information Processing Systems (NeurIPS)
https://proceedings.neurips.cc/paper_files/paper/2022/hash/6ad68a54eaa8f9bf6ac698b02ec05048-Abstract-Conference.html
|
这篇论文提出了一个由静电力学启发的生成模型 PFGM。该模型比扩散模型更为鲁棒;且在有扩散模型相同或者更优的生成质量情况下,生成速度更快。 |
[10] Yuan, Yang. On the power of foundation models. International Conference on Machine Learning. PMLR, 2023.
https://proceedings.mlr.press/v202/yuan23b.html
|
这篇论文通过范畴论视角刻画了大模型的能力边界,并提供了一个用于监督和自监督学习的范畴论框架。 |
[11] Yuan, Yang. A Categorical Framework of General Intelligence. arXiv preprint arXiv:2303.04571 (2023).
https://arxiv.org/abs/2303.04571
|
机器是否能思考?由于缺乏通用智能的坚实数学基础,至今无人能直接回答这一问题。本文提出一个关于通用智能的范畴论框架,利用范畴论,论文中许多通用智能的重要概念可以被严格定义和分析。 |
出品:漆远、吴力波、张江
运营:孟晋宇、王婷
撰稿:张江、杨燕青、王婷、王朝会、十三维、周莉、梁金、袁冰、江千月、刘志毅
鸣谢(按姓氏拼音顺序,排名不分先后):
曹风雷 、陈小杨 、程远、杜沅岂 、段郁、方榯楷 、付彦伟、 高悦、黄柯鑫、李昊、刘圣超、谭伟敏、吴泰霖、吴艳玲、向红军、张骥、张艳、朱思语
AI+Science 读书会
10. 加入集智,玩转复杂,共创斑图!集智俱乐部线下志愿者招募










