决策之桥:数据驱动优化方法的进展与挑战

导语
在当今大数据时代,数据已成为推动决策的核心资源。然而,如何将海量数据转化为最优决策,仍是学术界和工业界面临的重大挑战。近日北京大学宋洁教授团队在Cell Press交叉学科期刊Nexus发表题为《Bridging Prediction and Decision: Advances and Challenges in Data-Driven Optimization》的观点性综述文章,系统探讨了数据驱动的方法在预测和决策领域的应用。文章系统总结了序贯优化(SO)、端到端学习(E2E)和直接学习(DL)三种数据驱动型优化方法的理论、优势和最新进展,并结合能源调度、运筹管理和智能控制等典型应用场景进行了分析,通过剖析数据质量、优化建模和决策应用等关键问题,文章提出了对应的解决方案,为面向复杂环境的智能决策提供了重要的理论支撑和方法指引。
关键词:优化,序贯优化(Sequential Optimization,SO),端到端学习(End to End Learning, E2E),直接学习(Direct Learning, DL)
陆怡舟丨作者
曾利丨审校

论文题目:Bridging prediction and decision: Advances and challenges in data-driven optimization
论文地址:https://www.cell.com/nexus/fulltext/S2950-1601(25)00004-X
论文来源:Nexus
背景知识
背景知识
从石器时代的生存选择到数字时代的智能决策,人类文明的发展史也是一部决策能力的进化史。随着决策科学正经历从”经验驱动”到”数据驱动”的范式革命,现代决策问题越来越依赖于系统化的解决方法——通过将复杂的决策需求转化为可计算的优化问题,我们得以在数据海洋中寻找最优解,下面让我们通过两个典型决策问题来深入理解这一过程。
装载问题(个人决策):假设有一辆载重量上限为B的货车来到货场,需要从n件货品中选择部分货物进行装载。每件货物i的重量为ai,价值为ci。车主的目标是在不超过货车最大载重量B的前提下,选择若干件货物,使得被选中的货物的总价值最大。
如果定义这样的一个辅助决策变量: ,那么装载问题可以写为如下的优化问题。
,那么装载问题可以写为如下的优化问题。
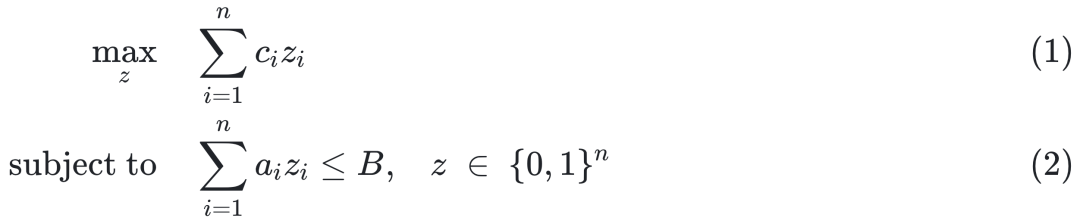
电网最优潮流控制问题(企业决策):在电力系统运行中,最优潮流控制问题的核心目标是通过调整发电机组的输出功率等可控参数,在满足节点正常功率平衡及各种安全指标的约束下,实现系统运行的目标函数最小化。假如某火电厂有n台火电机组,每台机组的输出功率为zi,机组的成本函数是输出功率的二次函数,即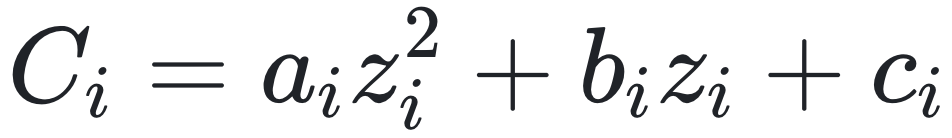 。火电厂面临两个约束,一是每台机组的输出功率需要保持在最佳运行功率区间
。火电厂面临两个约束,一是每台机组的输出功率需要保持在最佳运行功率区间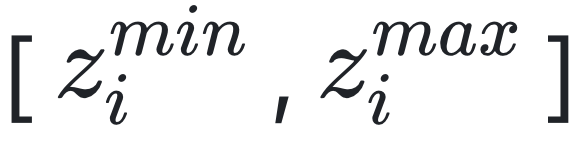 之内,同时,所有机组的总输出功率不能低于某个数值L。同样地,火电厂的决策问题也可以写为一个优化问题。
之内,同时,所有机组的总输出功率不能低于某个数值L。同样地,火电厂的决策问题也可以写为一个优化问题。
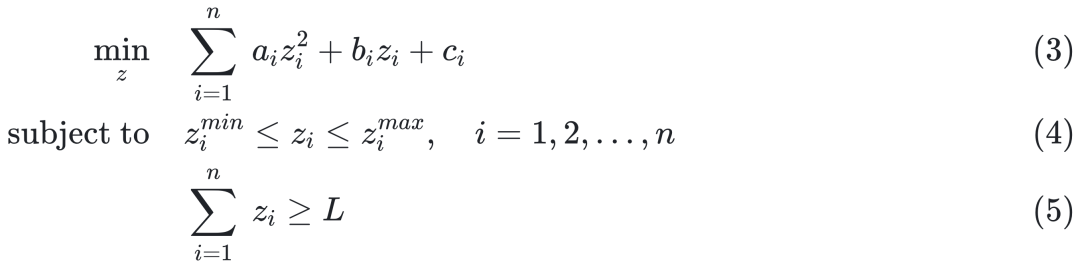
从前述的两个决策问题的例子出发,可以将决策问题一般化为如下形式:
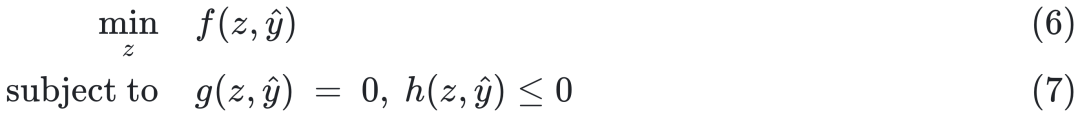
这里的z代表了决策变量,![]() 可以进一步参数化为pθ(x),代表了从输入变量(环境变量)x对某个相关变量(中间变量、内部变量)y的预测值。并且注意到,这个预测值
可以进一步参数化为pθ(x),代表了从输入变量(环境变量)x对某个相关变量(中间变量、内部变量)y的预测值。并且注意到,这个预测值![]() 可能与真实值y相等,也可能与真实值y之间存在偏差。对装载问题来说,不同货物的重量和价值均事先已知,
可能与真实值y相等,也可能与真实值y之间存在偏差。对装载问题来说,不同货物的重量和价值均事先已知,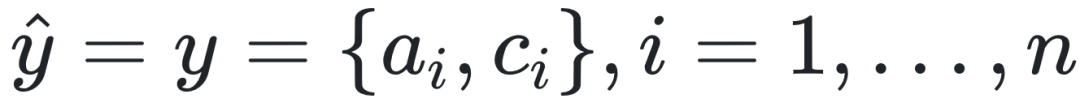 ,预测值与真实值是相等的。对于电网控制问题来说,成本方程(3)的各项系数是未知的,预测值
,预测值与真实值是相等的。对于电网控制问题来说,成本方程(3)的各项系数是未知的,预测值![]() 与真实值y={ai,bi,ci},i=1, …,n 很可能不相等。
与真实值y={ai,bi,ci},i=1, …,n 很可能不相等。
在复杂的现实决策问题中,所需要预测的变量y的形式更加多样,预测问题更加困难。例如,在能源市场的相关决策问题中,通常需要对电力价格、电力需求、风光新能源发电量等进行预测,往往会涉及复杂的经济社会系统、气象系统的预测问题。
随着机器学习和深度学习技术的飞速发展,“预测+决策”框架作为人工智能与系统科学相结合的重要手段,逐渐成为提升系统效能的核心挑战,也是最终实现大数据价值转化的关键途径。宋洁教授团队的综述文章从理论、应用、挑战和解决方案四个维度深入分析数据驱动的优化方法。
从预测到决策:数据驱动优化的三大范式
从预测到决策:数据驱动优化的三大范式
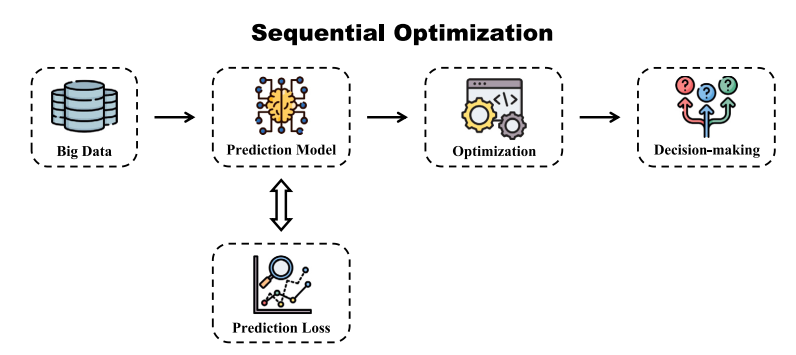
图1:序贯优化方法(范式一)
序贯优化方法(Sequential Optimization,SO):该方法采用“预测”-“优化”两阶段流程来解决决策问题:首先利用预测模型对不确定因素进行估计,再将预测结果输入优化模块生成决策。此方法直观且模块化,各环节可独立优化,实现人工智能与决策模型的直接耦合。常用的实现为第一步是通过数据驱动的方法,发现数据所代表的复杂系统的潜在运行模式,从而得到预测值![]() 。第二步再借助Gurobi等优化求解器,求解优化(公式 6-7)。
。第二步再借助Gurobi等优化求解器,求解优化(公式 6-7)。
但是,由于序贯优化方法将决策问题解耦成两个子问题,很可能产生优化阶段和决策阶段之间的不一致情况。在优化阶段,由于预测的精度有限,预测值![]() 往往是对称分布在真实值y的周围。但是决策阶段面对的备择情景却未必有类似的对称性[1]。仍然以电力行业面临的问题为例,如果预测值偏高,可能备择方案会增加不必要的操作资源,导致无效的资源分配。而如果预测值偏低,备择方案可能会触发网络之间的再平衡,带来额外系统可靠性问题。
往往是对称分布在真实值y的周围。但是决策阶段面对的备择情景却未必有类似的对称性[1]。仍然以电力行业面临的问题为例,如果预测值偏高,可能备择方案会增加不必要的操作资源,导致无效的资源分配。而如果预测值偏低,备择方案可能会触发网络之间的再平衡,带来额外系统可靠性问题。
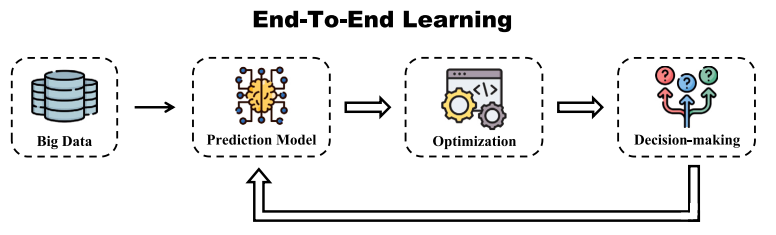
图2:端到端学习方法(范式二)
端到端学习方法(End to End Learning,E2E):也称为决策驱动学习。该方法将优化结构嵌入训练过程中,通过决策反馈直接调整预测模型,实现从预测到决策的闭环学习,从而更好地对齐预测与决策目标,有助于减少序贯优化方法中存在的偏差问题。具体来说,该方法将最优决策目标 表示为预测值的函数
表示为预测值的函数 ,从而将决策问题的目标(公式6-公式7)转化为最小化以下损失函数(也称为决策问题的后悔函数):
,从而将决策问题的目标(公式6-公式7)转化为最小化以下损失函数(也称为决策问题的后悔函数):
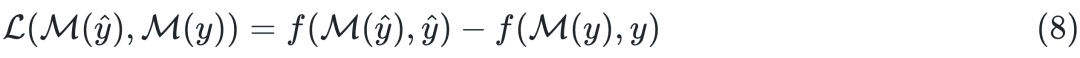
于是可以进一步通过计算(8)的梯度,利用梯度反向传播等方法得到最优决策解。
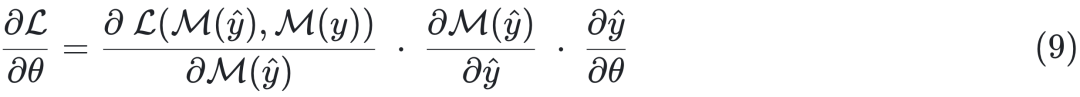
但是,(9)式往往难以显式表达,或者在实际问题中计算量巨大。一般可以通过三类E2E方法求解:隐函数方法(Implicit differentiation methods)、代理损失函数法(Surrogate loss methods)、近似求解法(Approximation methods)。隐函数方法通过优化问题的KKT条件将(9)式表示成雅可比矩阵的相应形式。代理损失函数法以SPO+损失函数为代表,将公式(9)转化为更易求解的SPO+损失函数的梯度形式[2]。近似求解法通过对预测值![]() 叠加高斯噪声ϵZ,并计算其期望值,即决策问题的扰动解
叠加高斯噪声ϵZ,并计算其期望值,即决策问题的扰动解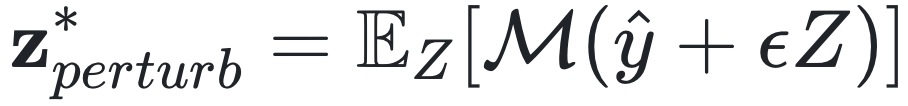 。
。
即便如此,E2E方法仍然受到优化问题(公式 6-7)这一框架的限制,在一些问题上的迭代计算任务仍然繁重。因此出现了通过在线深度强化学习[3,4]、网格搜索、随机搜索、贝叶斯优化[5]来减少计算量的方法。另外,E2E方法的泛化能力(Transferability)也是个问题。这主要由于E2E方法牺牲了预测性能,来保证决策问题的优化性能,因此其预测值可能与真实值偏离较大(图2-C、D),也导致其泛化能力不佳。
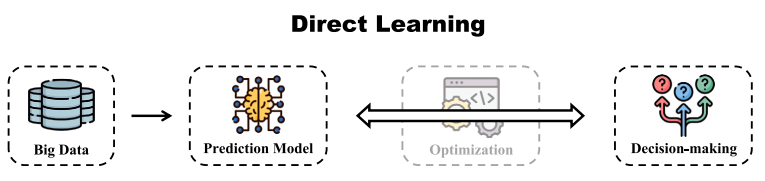
图3:直接学习方法(范式三)
直接学习方法(Direct Learning,DL)则另辟蹊径,不去求解优化问题(公式 6-7),转而寻找输入变量x与决策变量z的直接关系,该方法主要适用于那些优化问题结构复杂或隐式表达的场景,在难以明确定义优化过程时表现出卓越的适应性和灵活性。例如,在强化学习(Reinforcement Learning,RL)框架下,主要目标是求解马尔可夫决策过程(Markov Decision Process,MDP)的奖励值最大化, ,
,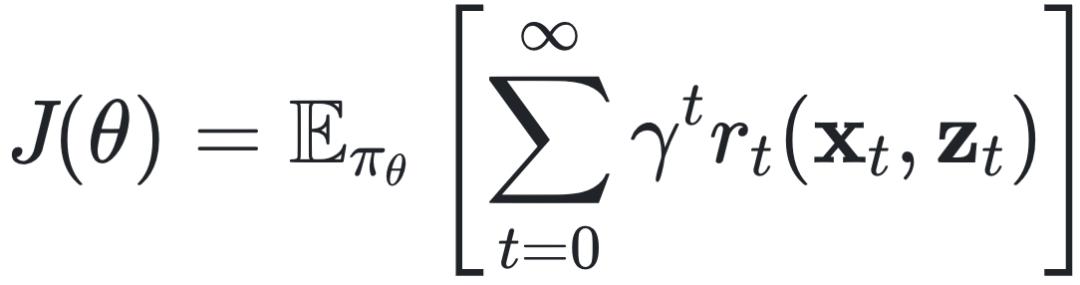 ,γ是折现系数,rt(xt, zt) 是奖励函数。又如在模仿学习(Imitation Learning,IL)框架下,主要目标是求解网络参数Φ,使得模仿网络的行为与专家示范数据尽可能一致,
,γ是折现系数,rt(xt, zt) 是奖励函数。又如在模仿学习(Imitation Learning,IL)框架下,主要目标是求解网络参数Φ,使得模仿网络的行为与专家示范数据尽可能一致,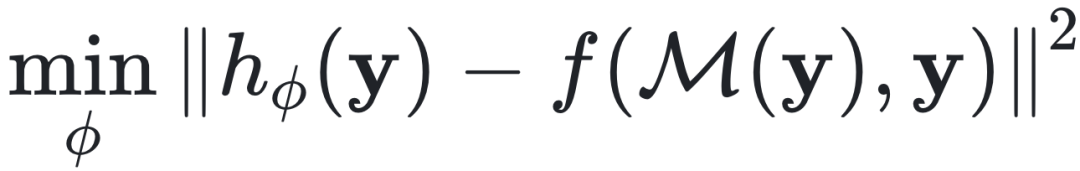 ,这里的y表示专家示范数据。
,这里的y表示专家示范数据。
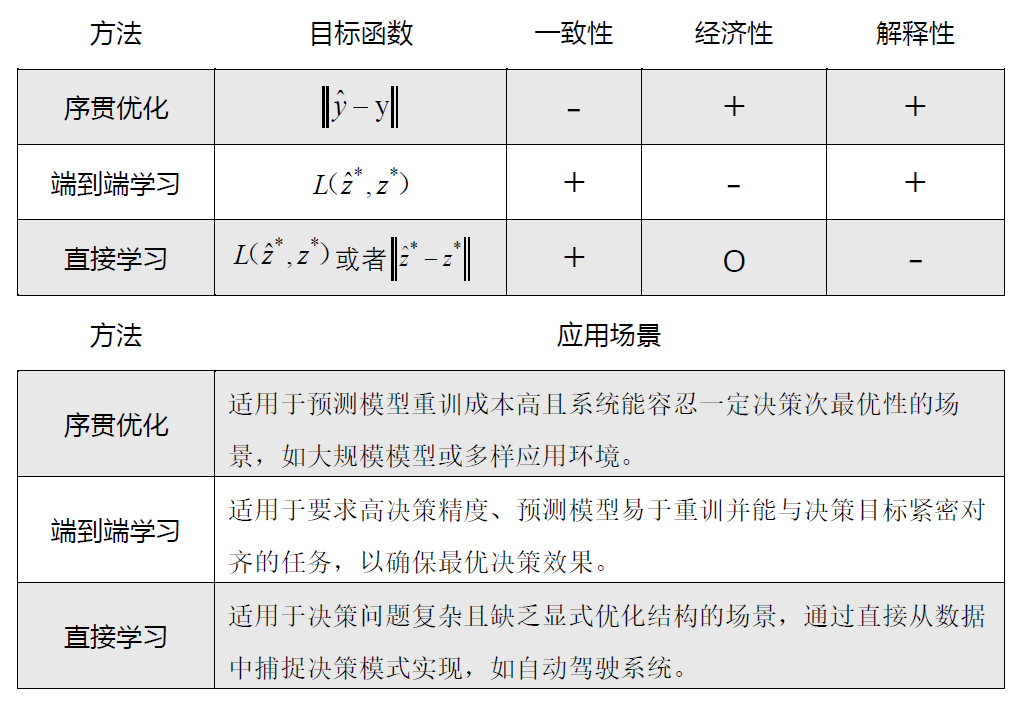
图4:三种数据驱动优化范式之间的比较
三类方法均有不同的特点和适用范围,简单对比总结为:
1.序贯优化方法的可解释性强、计算有效性较好,适用于对预测要求较高,预测模型重训练难度较大的大型问题(如NLP、气象问题),同时可以接受一定程度的次优决策;
2.端到端学习方法的一致性强、可解释性好,适用于决策精度要求高的情景;
3.直接学习方法的一致性强、计算有效性相对较好,适用于复杂、动态的决策环境,比如自动驾驶领域等。
虽然三类方法均为数据驱动的优化方法,但是序贯优化方法一般作为基线方法的角色出现。在目前大部分的数据驱动应用场景里,比如电力网络规划、复杂系统优化、能源系统节能、货物快递、港口管理、自动驾驶等,端到端学习方法和直接学习方法在效果上都要胜过序贯优化方法。
从理论到应用:
数据驱动优化方法面临的挑战
从理论到应用:
数据驱动优化方法面临的挑战
相较于基于先验知识和模型的传统决策方法,数据与预测技术的融合显著提升了实际应用效能。例如,通过整合大规模气象数据与地理信息,可实现更精准高效的可再生能源预测,进而借助多尺度人工智能模型使微电网中的分布式发电更智能高效。此外,针对发电企业与电网运营商普遍面临的管理难题,IBM、Oracle等行业巨头已开发出大数据驱动的智慧能源管理产品与服务,广泛应用于资产密集型产业。总体而言,数据输入与预测分析等技术的出现为决策应用注入了新活力,推动行业实践与标准实现质的飞跃。
文章通过三个微型案例研究,分别展示数据驱动优化方法在电网调度、市场运营及无人自动控制等不同领域的多元化应用。这些案例凸显了各类技术在应对复杂决策挑战时具有的跨领域适用性与实效性。
电力调度:Wahdany等人[6]利用KKT条件 (Karush-Kuhn-Tucker conditions) 来解决高风电电网的潮流控制问题,他们使用的端到端学习方法要比序贯优化方法减少了8.5%的网络拥堵和过载问题。Zhou等人[7]使用LSTM预测方法求解电网中的混合线性规划(Mixed-Integer Linear Programming, MILP)问题,降低了0.4%的运营成本。Sang等人[8]使用SPO+损失函数,根据电价来优化储能系统行为,比序贯优化方法提高了6.11%的经济效益。
市场运营:Chu等人[9]利用SPO+方法解决末端送货问题,与序贯优化方法相比减少了5%的运输成本。Tian等人[10]在端到端学习框架下求解港口巡检问题,比序贯优化方法减少每艘船只1%的运营成本。Qi等人[11]提出了不确定需求下的库存管理的直接学习框架,比序贯优化方法平均降低26.1%的持有成本[注:包括资金成本、仓储成本、保险成本和库存贬值成本,反映了持有库存所带来的一系列费用]和51.7%的缺货成本[注:包括销售损失、客户流失成本、紧急采购成本和生产中断成本,反映了因库存不足而带来的损失]。
无人自动控制:在自动驾驶、无人机控制、机器人领域,由于环境和控制任务的复杂,决策目标的优化问题的显式表达几无可能。这类问题广泛使用直接学习方法求解。比如,Cao等人[12]引入动态置信感知强化学习算法,来处理自动驾驶车辆在极端条件下的不确定性问题。Kim等人[13]使用强化学习方法训练无人机,整合无人机的形变传感数据、姿态数据、风向风速数据,来实现最优飞行。
针对数据驱动优化理论在行业应用情况,文章从“数据质量–建模优化–决策应用”的全流程分析挑战并提出相应技术性解决方案。
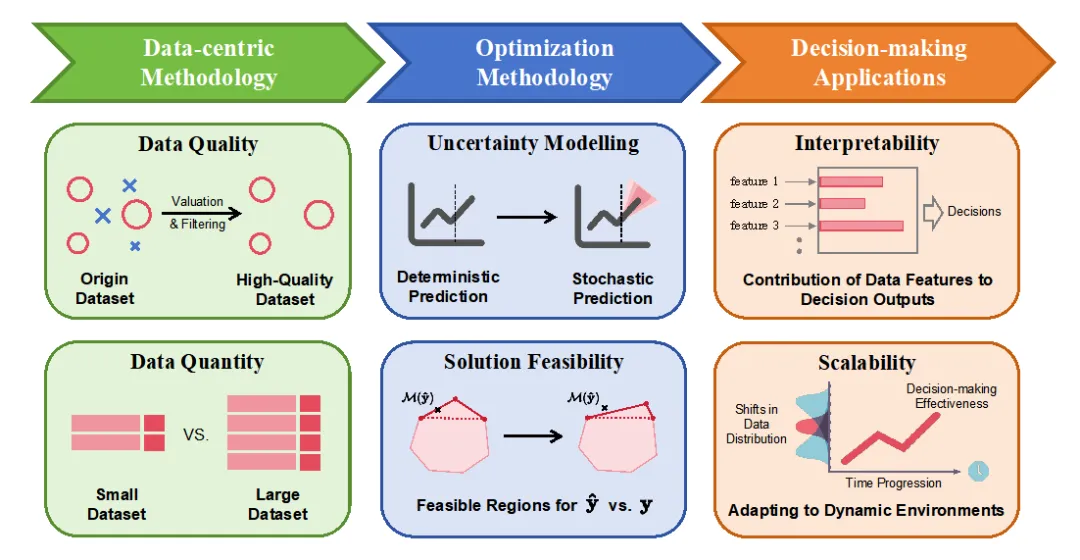
图5:数据驱动优化方法在实际应用中的挑战
上图显示了数据驱动优化在实际应用场景中面临的三大挑战,具体来说包括以下三个方面:
数据的质量和数量决定了决策的效果和效率。从数据质量来看,数据驱动方法要求对数据进行良好的预处理。传统的无监督的数据预处理方法包括一致性分析[14]、香农熵[15]、例外点监测[16],但是由于决策问题的复杂性,数据的重要性很可能是与决策条件相关的。为此,需要引入如动态分布方法[17]之类的有监督的数据预处理方法,来增加决策阶段的数据质量。这方面的研究仍然处于相对早期阶段。从数据数量来看,数据量太少可能造成过拟合问题,太多则可能增加训练成本和计算时间。在数据数量和决策效果之间取得平衡,仍然是一个关键的研究课题。对大样本而言,需要确定最优采样度[18],对小样本而言,则需要引入数据增广等技术[19,20],以及小样本学习方法[21]。
不确定性建模和解的可行性决定了优化方法的效能。在不确定性建模方面,方法的应用先于理论指导。近十年来,涌现了基于期望的隐函数法[22]、随机约束[23]、稳健优化[24,25]等方法,但是不确定性建模的理论分析仍然滞后。在解的可行性方面,最大的挑战来自于如何在E2E等方法应用过程中,仍然保持解的可行性。虽然如增加惩罚项[26]、引入风险项[27]、动态调整约束项[22]等方法能在一定程度上保证可行解,但是完整的理论分析框架仍然有待建立。
可解释性和可拓展性决定了决策方法的应用范围。可解释性一方面能够增强决策者对决策方法的信心,另一方面还有助于增加决策者对决策问题的洞见。机器学习领域出现了一些有效的解释性方法,包括LIME(Local Interpretable Model-agnostic Explanations),通过局部近似的方式,为复杂的“黑箱”模型提供可解释性,帮助用户理解模型在特定预测上的决策依据。以及 SHAP(SHapley Additive exPlanations),利用公平分配合作博弈收益的 Shapley Value,计算每个特征对模型预测的贡献,帮助用户理解模型的决策过程。但是将解释性方法从机器学习领域拓展到决策理论,仍存在较大挑战。可拓展性指模型在动态环境、不稳定分布条件下仍然能取得良好效果的能力,是模型能够跨领域跨行业应用的重要衡量。模型不可知的元学习方法[28]、在线学习方法[29]、小样本学习方法[30]都是保证可拓展性的重要方法类型。
结论
结论
大数据深刻的改变着人们的生活,数据科学同样深刻的改变着人们的决策行为。在数据驱动的优化方法推动下,决策问题的求解将变得越来越便捷、快速。从Nexus的这篇论文可以看到,数据优化的驱动方法经历了三次更迭,从序贯优化到端到端学习优化再到直接学习方法,模型的内在一致性更强,计算效率更高。虽然,这些方法在数据方法论、不确定性、解的可行性、可解释性和可拓展性方面都存在挑战,但随着数据科学、优化理论的发展,新的决策方法将在更广阔的领域得到应用。数据驱动的决策科学将是一个有生命力的、方兴未艾的研究领域。
参考文献
-
Zareipour, H., Canizares, C.A., and Bhattacharya, K. (2010). Economic impact of electricity market price forecasting errors: A demand-side analysis. IEEE Trans. Power Syst. 25, 254-262.
-
Elmachtoub, A. N., & Grigas, P. (2017). Smart “Predict, then Optimize”. arXiv preprint arXiv:1710.08005.
-
Bertsimas, D., and Stellato, B. (2022). Online mixed-integer optimization in milliseconds. Inf. J. Comput. 34, 2229-2248.
-
Tang, Y., Agrawal, S., and Faenza, Y. (2020). Reinforcement learning for integer programming: Learning to cut. In International Conference on Machine Learning (PMLR), pp. 9367-9376.
-
Feurer, M., and Hutter, F. (2019). Hyperparameter optimization. In Automated Machine Learning: Methods, Systems, Challenges (Springer International Publishing), pp. 3-33.
-
Wahdany, D., Schmitt, C., and Cremer, J.L. (2023). More than accuracy: end-to-end wind power forecasting that optimises the energy system. Elec. Power Syst. Res. 221, 109384.
-
Zhou, Y., Wen, Q., Song, J., et al. (2024). Load data valuation in multienergy systems: An end-to-end approach. IEEE Trans. Smart Grid.
-
Sang, L., Xu, Y., Long, H., et al. (2022). Electricity price prediction for energy storage system arbitrage: A decision-focused approach. IEEE Trans. Smart Grid 13, 2822-2832.
-
Chu, H., Zhang, W., Bai, P., et al. (2023). Data-driven optimization for last-mile delivery. Complex Intell. Systems 9, 2271-2284.
-
Tian, X., Yan, R., Liu, Y., et al. (2023). A smart predict-then-optimize method for targeted and cost-effective maritime transportation. Transp. Res. Part B Methodol. 172, 32-52.
-
Qi, M., Shi, Y., Qi, Y., et al. (2023). A practical end-to-end inventory management model with deep learning. Manag. Sci. 69, 759-773.
-
Cao, Z., Jiang, K., Zhou, W., et al. (2023). Continuous improvement of self driving cars using dynamic confidence-aware reinforcement learning. Nat. Mach. Intell. 5, 145-158.
-
Kim, T., Hong, I., Im, S., et al. (2024). Wing-strain-based flight control of flapping-wing drones through reinforce-ment learning. Nat. Mach. Intell. 6, 992-1005.
-
Cichy, C., and Rass, S. (2019). An overview of data quality frameworks. IEEE Access 7, 24634-24648.
-
Lin, J. (1991). Divergence measures based on the shannon entropy. IEEE Trans. Inf. Theor. 37, 145-151.
-
Blázquez-García, A., Conde, A., Mori, U., et al. (2021). A review on out-lier/anomaly detection in time series data. ACM Comput. Surv. 54, 1-33.
-
Ghorbani, A., Kim, M., and Zou, J. (2020). A distributional framework for data valuation. In International Conference on Machine Learning (PMLR), pp. 3535-3544.
-
Besbes, O., and Mouchtaki, O. (2023). How big should your data really be? data driven newsvendor: Learning one sample at a time. Manag. Sci. 69, 5848-5865.
-
Lata, K., Dave, M., and KN, N. (2019). Data augmentation using generative adversarial network. In Proceedings of 2nd International Conference on Advanced Computing and Software Engineering (ICACSE).
-
Mumuni, A., and Mumuni, F. (2022). Data augmentation: A comprehensive survey of modern approaches. Array 16, 100258.
-
Wang, Y., Yao, Q., Kwok, J.T., et al. (2020). Generalizing from a few examples: A survey on few-shot learning. ACM Comput. Surv. 53, 1-34.
-
Donti, P., Amos, B., and Kolter, J.Z. (2017). Task-based end-to-end model learning in stochastic optimization. Adv. Neural Inf. Process. Syst. 30.
-
Pr’ekopa, A. (2013). Stochastic Programming, 324 (Springer Science & Business Media).
-
Rahimian, H., and Mehrotra, S. (2019). Distributionally robust optimization: A review. Preprint at arXiv. https://doi.org/10.48550/arXiv.1908.05659.
-
Ben-Tal, A., El Ghaoui, L., and Nemirovski, A. (2009). Robust Optimization, 28 (Princeton university press).
-
Garcia, J.D., Street, A., Homem-de Mello, T., et al. (2021). Application-driven learning: A closed-loop prediction and optimization approach applied to dynamic reserves and demand forecasting. Preprint at arXiv. https://doi.org/10.48550/arXiv.2102.13273.
-
Zhang, H., Li, R., Chen, Y., et al. (2023). Risk-aware objective-based forecasting in inertia management. IEEE Trans. Power Syst.
-
Finn, C., Abbeel, P., and Levine, S. (2017). Model-agnostic meta-learning for fast adaptation of deep networks. In International Conference on Machine Learning (PMLR), pp. 1126-1135.
-
Hoi, S.C., Sahoo, D., Lu, J., et al. (2021). Online learning: A comprehensive survey. Neurocomputing 459, 249-289.
-
Parnami, A., and Lee, M. (2022). Learning from few examples: A summary of approaches to few-shot learning. Preprint at arXiv. https://doi.org/10.48550/arXiv.2203.04291.
参考文献可上下滑动查看
复杂系统自动建模读书会第二季
“复杂世界,简单规则”。
集智俱乐部联合复旦大学智能复杂体系实验室青年研究员朱群喜、浙江大学百人计划研究员李樵风、清华大学电子工程系数据科学与智能实验室博士后研究员丁璟韬、美国东北大学物理系Albert-László Barabási指导的博士后高婷婷、北京大学博雅博士后曹文祺、复旦大学数学科学学院应用数学方向博士研究生赵伯林、北京师范大学系统科学学院博士研究生牟牧云,共同发起「复杂系统自动建模」读书会第二季。
读书会将于9月5日起每周四晚上20:00-22:00进行,探讨四个核心模块:数据驱动的复杂系统建模、复杂网络结构推断、具有可解释性的复杂系统推断(动力学+网络结构)、应用-超材料设计和城市系统,通过重点讨论75篇经典、前沿的重要文献,从黑盒(数据驱动)到白盒(可解释性),逐步捕捉系统的“本质”规律,帮助大家更好的认识、理解、预测、控制、设计复杂系统,为相关领域的研究和应用提供洞见。欢迎感兴趣的朋友报名参与!
复杂系统自动建模读书会:从数据驱动到可解释性,探索系统内在规律|内附75篇领域必读文献
6. 加入集智,玩转复杂,共创斑图!集智俱乐部线下志愿者招募










