生命之流 | 从永动机到人工智能

生命之流

《生命之流》系张江老师2008年至2009年，利用闲暇时间所构思的一本科普集。主要内容包括：从复杂到生命、自主生命体简史、重新发现时间、从永动机到人工智能、连接上帝的纽带——熵等章节。现将已公开部分刊出，希望能够和大家共同学习。

牛顿力学2.0

虽然Autopoiesis理论从自我生产的角度给出了“生命软件”的一种广义描述，但是它却没有关注流动、能量、目的等生命系统中有关时间的概念。为了更透彻地理解它们，我们有必要走进物理的世界，看看物理学家们这几百年来是如何认识这些概念的。

让我们把记忆的时钟拨回到高中时代，在那时我们学到了牛顿力学。受力分析、运动分析、牛顿第二定律、问题求解几乎可以构成高中物理解题的几个标准步骤。如果我们把整个分析流程编制成计算机程序，那么只要输入初始位置、速度和边界条件等基本信息，该软件就会输出一个轨迹方程，它描述了任意时刻，系统所处的位置、速度等全部信息。时间t作为一个自变量就出现在系统输出的轨迹方程之中。这个方程就好比是一盒录像带，上面记录了系统未来的全部图景。你想获知100年之后系统的情况吗？没问题，只要你把录像带“倒到”100年那里就能看到全部你想要的图景了（相当于把t=100年代如到了轨迹方程中）。为了使表达更加清晰，同时避免浪费过多的篇幅在细节上，我们将在框中给出一个具体的实例，读者可以有选择地跳过。

例1：为了领略经典物理，让我们从一个非常简单的实例开始。

图3.1 一个简单的力学系统

如图(a)，一个物块（为简单，质量m=1）绑在一根弹簧上，在一个光滑水平面上往复运动，初始时刻物块位于位移s=0的点，且初速度为v0。(b)为物块m的受力分析图，竖直方向重力和地面的支持力平衡，水平方向仅仅受一个向回拉的弹簧拉力，它的大小是ks，其中s为弹簧伸长长度也就是物体的位移（将坐标原点取到弹簧的自然伸长处），k是一个常数，为了简单，设k=1。

根据物块m的受力分析（图3.1(b)），我们可以写出制约m的牛顿第二定律方程：

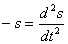（1）

其中-s就是物体所受到的合外力F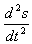，是物体的加速度a，所以上式就是牛顿第二定律F=ma。这是一个关于位置s(t)的微分方程，代入初始条件(s(t)=0, s′(t)=v₀)，求解该方程，可得：

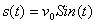（2）

求一阶导数可得物块任意时刻速度：

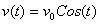（3）

这样，物块的全部信息（包括历史和未来）就都包含在这两个式子里面了。我们只要把t=100代入（2）和（3）就能立即得知100秒后物块的位置和速度了。

然而，这种高中求解输出录像带的方法并不总能奏效。因为在有些时候，牛顿第二定律给出的微分方程可能非常复杂，以至于不能求解（并不是所有的微分方程都能给出显式解）。因此，我们有必要介绍第二种方法。早在19世纪，大数学家彭加莱（Poincare）为了证明有多个天体构成的太阳系系统是稳定的，专门发展了一套数学方法叫做动力系统。该方法既来源于早期的牛顿力学，同时又大大扩展了牛顿力学的应用范围，下面我们将主要探讨这种方法。

如果我们把之前讲的高中物理求解软件叫做牛顿力学1.0，那么动力系统方法就相当于是它的升级版本，所以称之为牛顿力学2.0。同样，你把系统的初始位置、速度等信息输入给它，它将给你输出结果。但是，与牛顿力学1.0最大的不同在于，2.0并不输出一盘记录系统全部未来信息的录像带，而是一个好玩的计算机模拟游戏。你想知道系统100年之后的样子吗？“可以，不过，对不起，您必须等到我一秒一秒地算到100年之后再说”，牛顿力学2.0回答道。

我们可以把牛顿力学2.0看作由两部分构成<X,f>，其中X叫做系统的状态空间，f叫做演化规律。设在t时刻，系统的状态为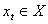，那么在下一时刻系统的状态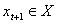就将由下面的方程决定：

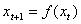（4）

这样，只要我们给出系统在t=1时刻的状态即x₁，我们就能通过（4）算出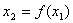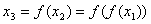，……，等等全部信息。

对于一个物体来说，我们可以把它的位置x和速度v都看作是物体的状态。这样，该物体所处的状态空间就是{(x,v)|x∈R,v∈R}。演化方程（4）可以具体地从牛顿第二定律导出，请看下面框中的例子。

例1：

针对例1的情况，我们可以用牛顿2.0的方法再对它进行讨论。首先，如果设速度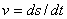，那么可以把（1）式重新写为：

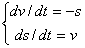（5）

这样，原来的一个包含二阶导数的微分方程变成了两个一阶的微分方程。第一个方程实际上就是牛顿第二定律即加速度乘以质量等于合外力，第二个方程是速度的定义，即位置对时间的一阶导数。方程的右边可以看作两个变量：位置和速度的函数。这种左边是一阶导数，右边是函数的方程或者方程组就叫做微分动力系统（此处不展开讨论）。为了得到牛顿力学2.0的形式，我们把（5）离散化，即把该问题变为一个跌代程序。不妨设时间间隔dt=0.0001，这样（5）就变为：

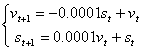（6）

这个方程就变成了一个离散动力系统的递推方程，它可以给出和方程（2）、（3）相近的答案（如果dt取得越小，则答案越接近）。

该系统的状态空间是(s,v)两个变量的所有可能组合，演化规律f是：

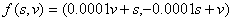（7）

我们把初始速度和位置代入方程（即令s₀=0, v₀₌v₀），它就能算出新的v和s：v₁=v₀, s₁=0.0001v₀，再把这对新的值代入，得到：v₂=v₀, s₂=0.0002v₀，……。这样，虽然我们没有求解微分方程，但是仍可以用计算机一步一步地算出物块的位置和速度。在一般情况下，无论（5）能不能求解出来，我们都可以用计算机来求解（6），因此它具有更普遍的意义。

牛顿力学2.0也能够描述多个体的系统，只要我们适当扩大系统的状态空间就可以了。例如，我们考虑台球桌上的n个小球互相撞的系统，每个小球都可以用4个变量来表示(x,y,v_x,v_y)，其中x,y表示小球的坐标，v_x,v_y表示小球沿水平方向和竖直方向的速度。那么n个小球就可以用4n个变量来表示。所以系统的一个状态就是这4n个变量的一种可能取值的组合，如(1,3,0.2,0.3,2,1,0.1,0.2…)就表示第一个小球的位置是(1,3)，速度是(0.2,0.3)，第二个小球位置是(2,1)，速度是(0.1,0.2)……。这样状态空间X就被扩大成4n维的空间了。系统的演化f也可以相应地写出来，但是这种情况下，给出类似（7）的数学表达式还不如直接写成计算机程序。

从计算机模拟的角度来看，系统的状态就相当于是存储于计算机内存中的数据，而系统的一步演化就相当于是计算机CPU的一次计算。这样，系统下一时刻的状态就可以用规律f作用到上一时刻的系统状态（数据）而得到。所以这样看来，很多计算机模拟程序，如细胞自动机、多Agent模拟系统都可以看作是牛顿力学2.0的特例。

因为计算机模拟程序并没有限制X和f是具体什么样的数据和程序，所以我们就可以进行大胆的抽象，设计出各种奇形怪状的模拟宇宙。我们完全可以让X中的元素变成桌子、烂袜子或者抽水马桶，f也并不一定非得是牛顿定律、量子力学，而可能是“魔兽世界”或者“第二人生”。数学对物理的抽象能够让我们再造出完全不同的“虚拟物理”！

虽然数学的确具有一定的“超越物理的数学实在性”，但是不可否认，具体的X和f会有不同的性质。那么这些不同性质的f和X究竟能够创造出什么样的物理呢？这是一个更加深刻的问题。

例如，如果f是个一一映射函数，那么该动力系统就是可逆的。

f是一一映射意味着给定一个x数值，有一个唯一的数值f(x)与之对应。反之，给定一个数值y，我们总能找到一个对应的x，使得f(x)=y。这样，函数f(x)=x³就是一对一映射，而f(x)=x²就不是（因为给定y=4，我们既可以找到f(-2)=4，也可以找到f(2)=4）。如果f是一一映射函数，那么它的逆函数f^-1就必然存在。假设系统在10个时间步内的演化可以看作是从x_t经过f得到x_t+1，再得到x_t+2，……x_t+10的过程。那么反过来，从x_t+10开始，通过f^-1我们能够得到x_t+9，x_t+8，……，最后应用10次就可以得到x_t，如图3.2。所以这个新的动力系统(X,f^-1)就是原系统(X,f)的逆系统，它所得到的过程(x_t+10,x_t+9, …,x_t)就是对过程(x_t,x_t+1,x_t+2,…,x_t+10)的回放。所以，我们说动力系统(X,f)是可逆的。

图3.2 可逆动力系统

经典物理已经证明，从牛顿第二定律F=ma得到的动力系统都是可逆的。

在例1中，由于(7)式是个一一映射函数，因此它是可逆的，逆函数是：

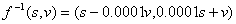（8）

这一点我们也可以从直观上看出来，实际上，物块朝右运动和朝左运动情况是完全一样的。

可逆动力系统没有我们常说的时间之箭，因为系统朝前演化和朝后演化是等价的，只要按照逆映射，我们可以从t+10时刻的状态完全恢复t时刻的状态。如果系统是不可逆的，那么系统就只能朝向时间的一个方向演化，因此，时间之箭的问题在动力系统中就明显突现出来了。

一般的X具有非常多的维度。例如， n个小球构成的台球系统的状态空间就有4n维。考虑这么一个大维度的空间是很麻烦的，所以人们常常会将状态空间X进行压缩，即找到一个描述系统状态的函数M(x) ，让它在实数范围内取值（简称状态函数）来判明X以及动力系统的性质。因为系统的状态会在f的作用下不断发生变化，所以我们就能画出M(x(t))随着时间的函数曲线。最常见的有几种情况：

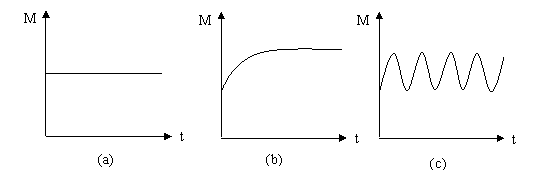图3.3 压缩的状态空间同时间的关系

图3.3(a)表示状态函数随时间没有任何变化。例如，我们可以计算经典物理系统中的总机械能来作为函数M，如果系统是忽略摩擦的，那么机械能就不随时间而变化，所以，我们也说能量是一个守恒量。

对于我们那个物块的例子来说，系统的机械能（势能+动能）是：

（9）

这是一个状态x=(s,v)的函数。因为状态在f的作用下会随着时间t不停地变化，所以有可能E也会随着时间变化。在这个例子中，我们能够求解（1）式得到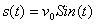和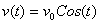，代入（9）式就得到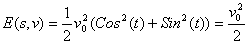。我们看到总机械能是一个不包含时间的常数v₀²/2，这也就意味着能量是一个守恒量。

更一般的，只要我们能够找到一个从系统的状态空间X到1维实数空间R的映射M: X–>R，使得M在f的作用下保持不变，即M(x)=M(f(x))，那么我们就找到了一个相应的该系统的守恒量。符合图3.3(a)的函数M都可以看作是系统的守恒量，例如在一些经典物理系统中，总动量或者总角动量就都满足这个性质。

图3.3(b)表示状态函数随时间不断增长并趋向一个固定值的情况。这说明系统的演化将趋向一类特殊的状态，这些特殊状态就好比是系统演化的“目的”或者“趋向性”。我们来看一个简单的例子（例2），如下图：

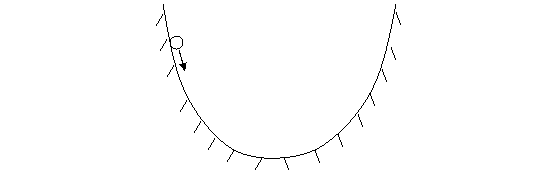图3.4 在一个U形轨道上滚动的小球

假设在一个粗糙的U形轨道上，一个小球从侧壁滚下来。可以预料到，小球三晃两晃将会停在U字形的谷底。对这个物理现象的解释当然可以用牛顿力学2.0求解，对式（9）那样的方程进行反复跌代必然会得到小球将停在谷底的结果。但是，这个计算过程太复杂了，我们还可以用一种不一样的方法求解出小球最后的平衡状态。由于整个轨道位于一个重力场中，决定小球运动的也主要是重力，所以我们可以计算小球的势能，于是谷底也就对应了势能的最小点。根本不用费力计算小球在每时刻的受力，物理学家就可以轻松地告诉你，最后小球一定停在最低点。这是因为，小球的运动将会使得势能最小化。进一步我们可以把小球具有的势能看作映射M，那么我们不难画出M随时间变化的曲线，如下图：

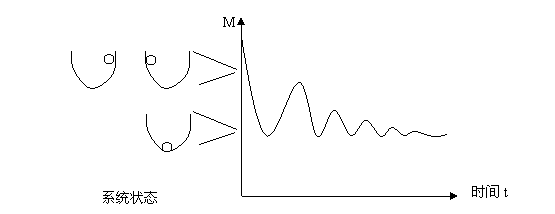图3.5 小球落入谷底粒子中M同时间的关系

虽然与图3.4(b)中的曲线略有不同，但是图3.5的曲线也将趋向于一个固定的数值，这一数值刚好对应小球所处的谷底状态。其实通过简单的数学变换，我们可以把趋向一个最小值的情况转变为趋向最大值的情况，如可以计算-M的曲线，这样就能得到与图3.4(b)相同的结果。图3.4(b)所表示的就是一个具有“目的性”的物理系统，因为我们可以拟人地说小球的目的就是为了让势能最小化。恰恰是可以利用系统的目的性，我们才可以直接计算出系统的平衡状态结果，而不需要更复杂的迭代计算。

假如这个例子中的小球在一个光滑的曲面上滚动，那么如果再次画出小球势能同时间的关系就能得到类似图3.4(c)中的结果。这种结果在很多具有周期行为的系统中都很常见。图3.4(a)和(c)这两种情况都显示出系统的行为对时间的某种对称性。(a)情况为一个与时间无关的状态函数，在时间轴上就相当于是处处对称的。(c)则是关于时间平移对称的，只要我们在时间轴上平移固定的周期长度，那么我们将不能分辨时间点。而只有在(b)这种情况下时间才是系统的一个本质属性。因为随着时间的流逝，系统会趋向一个比较明显的“目的”。这样根据趋向该目的的程度不同，我们就能分辨出系统处于不同的时间点上。而且，时间的方向性也可以在这种情况下被分辨出来。假如时间反演，我们会看到系统的状态函数M将从一个数值开始发散出来，它的行为和正向演化是非常不同的。

总结来看，利用牛顿力学2.0的方式描述系统的演化具有更加抽象的数学形式。我们可以讨论具有不同数学性质的动力系统而得到不同的虚拟宇宙。虚拟宇宙中有关时间的属性就全部体现在X和f的数学性质之中了。玩过游戏的人都知道，一般的游戏世界跟我们的现实世界一样是时间不可逆的，死掉的超级马莉不可能再从坑里跳出来去采蘑菇。但是我们可以通过保留虚拟世界每一时刻的状态（相当于把状态空间X扩充以便系统可以存盘），让动力系统的f变成一个一一映射函数（即在游戏的演进过程中并不丢失任何信息），这样就能让系统变成可逆的。

给虚拟宇宙添加守恒的物理量可以让它的演化体现出一种时间上的平衡性，如在游戏世界中添加总守恒的财富就可能让系统变得更加平衡，因为它在时间上是对称的。而如果我们能够找到一个如图3.3（b）所示的状态函数，就能够预测出动力系统演化的平衡属性，因为系统将自发趋向于那个状态。所有这些讨论都不仅可以帮助我们更加深刻地认识我们所处的现实宇宙，而且还可以帮助我们设计不一样的虚拟世界，更重要的是它帮助我们从一种更加抽象的角度来认识时间。

热量中的时间之箭

上一章探讨的是经典物理世界，在那里系统的构成相对简单。本章将走入热力学的世界，我们面对的不再是简单的小球和弹簧，而是一个个庞大的热力学机器。更有意思的是，正是在热力学中，人们发现了牛顿力学世界中看不见的时间之箭。

我们的故事要从一种可以永远运动，并能源源不断地输出能量的机器讲起，这类机器就被称为永动机。永动机的思想可以追溯到古印度，十三世纪这一想法被传入了欧洲。早期最著名的一个永动机方案是一个较亨内考的法国人提出来的，如下图：

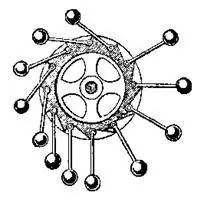
图4.1 一个设计巧妙的永动机，它试图利用左右不平衡的力矩来使得轮子永远转动

它试图利用右侧球-杆较大的力矩来驱动轮子永远转下去。然而当它真正工作的时候会很快就停下来了（你知道为什么吗？）。早期的很多永动机都与这个装置类似，即能够在不消耗能量的前提下获得源源不断的能量输出，这类永动机统称第一类永动机。

随着18世纪欧洲工业革命的爆发，大规模的工业生产迫切需要解决能源的问题。假如永动机真能实现，那就意味着人们不必再为能源问题发愁了。所以，那时人们对于永动机的追求更是达到了顶峰，法国科学院甚至在1775年宣布不再审查任何关于永动机的设计方案，因为所有永动机没有一个能真正成功。

人们开始认识到，宇宙是没有免费午餐的。似乎这里面蕴藏着自然界的规律，于是在大量实验的基础上，科学家Mayer（迈尔）和Joule（焦耳）等人提出了能量的守恒与转化原理即热力学第一定律否定了第一类永动机的可能性。从上一章介绍的动力系统和状态函数的观点来看，人们终于找到了整个宇宙的状态函数：总能量，它随时间的演化符合3.3(a)所示的情况。因此整个宇宙的能量既不增加也不减少，只能从一种形式转变成另一种形式。

然而，对于永动机的梦想，还有人不死心，他们认为虽然我们不能凭空创造能量，但却可以把所居住的环境（例如空气，或者海洋）看作一个大能源库。这样，只要我们能造出一台机器，它可以不断地从环境中吸收热量，把它们转变成有用的功进行输出，因为环境的能量是非常庞大的，那么我们不一样可以创造出永恒的能源吗？这一类机器就叫做第二类永动机，它们试图从单一热源吸热而做功。

第二类永动机也无疑例外地失败了，对于这类机器的否定使科学家们提出了热力学第二定律，它告诫人们只从单一热源获取热量的永动机是不能实现的。然而，第二定律仅仅是人们从实践之中总结出来的一条经验规律，究竟为什么会有这条规律？人们还不清楚。甚至人们还不知道如何用严格的科学方法来研究它。

正在这时，一个名叫Carnot（卡诺）的小伙子提出了一个理想模型：卡诺热机，为热力学第二定律的科学表达奠定了基础。卡诺热机代表了宇宙中一切机器的机械效率的极限：任何热机的机械效率都不可能高于卡诺热机。

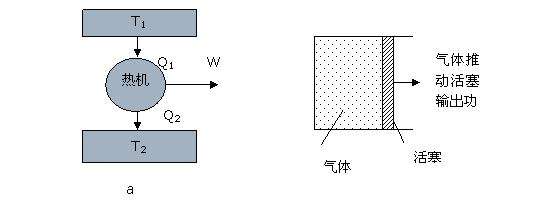
图4.2 任意一台热机的工作原理示意图

首先，我们需要说明什么是热机，如图4.2(a)，热机是一种机械装置，它会从高温吸收一定热量Q₁，然后向低温热源排出废热Q₂，同时向外界输出有用功W。图4.2(b)给出了一个具体的热机的例子。该热机由一个充满气体的气缸和一个可以滑动的活塞组成。当把这套东西跟一个高温热源（温度T₁）接触，气体会受热膨胀，活塞被推动对外界输出功。再把它跟低温热源接触，气体会丢失一部分热量到低温热源去，同时它还必须再次收缩到原来的体积以便重复刚才的过程。从吸热到放热的一系列动作就是一个循环，汽车上的发动机嘣嘣跳个不停就是一直在做这个类似的循环。

我们知道，对于任何一个可用的热机，都必须满足两个条件：（1）、这台机器需要工作在两个热源之间，一个高温热源T₁，一个低温热源T₂；（2）、在完成一个吸热、放热循环之后，机器必须还能恢复到原状，以便再次重复这一系列动作（否则我们的机器将不能持久输出能量）。

很显然，我们希望热机的输出功W越多越好。但是它却要受很多限制，首先，根据热力学第一定律（能量守恒），W<=Q₁，即能量不能无中生有。其次，根据热力学第二定律，热机不能从单一热源吸热而全部转化成有用功，所以Q₂>0，因此W必然<Q₁。在这些限制下，我们可以定义这台热机的效率为e=W/Q₁，所以e越大也就意味着W越大，但它不会大过1。那么，e能不能无限接近于1呢？卡诺告诉你，这也是不可能的。他证明，只要热机满足那两个条件，那么效率e最大也不能超过理想机器：卡诺热机所能达到的极限。

这是为什么呢？原因就在于卡诺热机的运作过程是一个理想化的过程，它忽略了所有的摩擦，而且它的运作要无限缓慢，使得每一步动作都是可逆的。如果我们把卡诺热机以及它周围的环境看作一个动力系统（牛顿力学2.0），那么上一章讨论过的可逆概念就可以用到这里来了。我们把对卡诺热机的每一步操作（例如推动一小步活塞）看作是动力系统的一次迭代（应用一次f函数），这样如果该操作是可逆的，那么必然存在一个可逆函数f^-1使得从之后的卡诺热机+环境的状态可以完全恢复到应用f之前的状态。我们知道忽略掉摩擦力的牛顿力学系统就是可逆的动力系统。所以，如果我们推动活塞无限缓慢，那么摩擦力的效果（摩擦力做功）可以忽略，这个过程就是可逆的。因此，卡诺热机就是可逆热机的代名词。

进一步，即使卡诺热机这样的理想机器为什么也不能使得效率达到100%呢？这是因为我们不仅要求输出能量，还要求机器能够持续地输出能量，即系统在完成了一个循环后还要回到状态原点，这就使得我们不得不耗费一些额外的能量来让系统恢复原状。理论上可以证明，工作在两个热源之间的卡诺热机效率仅仅是两个热源温度的函数，即(T₁-T₂)/T₁。同时可以证明，任何一个工作在同样热源之间的可逆热机，其机械效率都是(T₁-T₂)/T₁，而不可逆热机的效率都会小于这个数（这一点见框中的证明）。

对“在相同的高温和低温热源条件下，不可逆热机的效率小于可逆热机的效率”的证明。

运用反证法，假设高于可逆热机效率的机器存在，我们设它为H，它工作在热源T₁和T₂之间。它从高温热源吸热Q₁，做功W’，向低温热源输出热量Q₂。再考虑一个连接在T₁和T₂之间的卡诺热机C。假设它同样吸热Q₁，输出的功是W，同时放热Q₁-W。因为我们假设H的效率大于C的，所以吸收同样的热量的时候，W<W’。因为卡诺热机都是可逆热机，所以我们可以把C逆过来作为一个制冷机-C使用（即循环倒转：外界对机器做功，从低温热源吸热），它在外界做功W的条件下，从低温热源吸热Q₁-W，会向高温热源放出热量Q₁。如图：

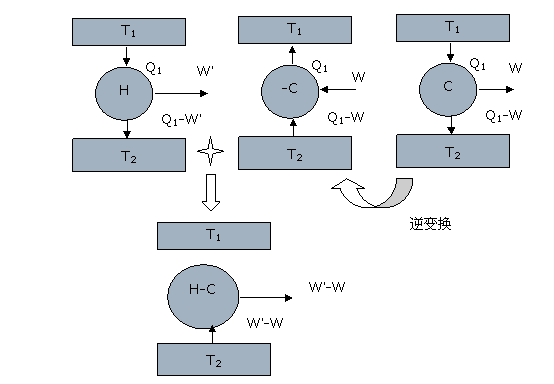
图4.3 对不可逆热机机械效率小于可逆热机的证明

之后，我们将H与-C合并构成一个新的热机：H-C，则H-C的净效果是从低温热源吸热W’-W，向高温热源输出热量0，同时对外界做功W’-W>0。这与第二定律矛盾（从单一热源吸热并全部转化成功），所以在相同条件下，不可逆热机的效率要小于卡诺热机效率。

卡诺的发现为理论家们打开了一扇窗，因为卡诺热机是一个漂亮的、干净的模型，所以物理学家就可以利用数学工具来探讨热力学第二定律了。我们看到，热不能从低温物体传向高温物体、不能把全部的热转变为功等等物理现象都来源于时间的方向性——即时间之箭。联系到上一章的讨论，如果我们能够找到一个系统的状态函数，它随时间的演化是按照图3.3(b)那样趋向于一个目标，那么我们就能从数学上揭示出时间的方向性。1865年，物理学家克劳修斯（Clausius）正是作了这样的事，通过研究卡诺热机，他终于找到了这样的状态函数，从而为热力学第二定律严格的数学基础。这个重要的状态函数就是：熵。

克劳修斯的出发点是把热机看作一个动力系统，系统的状态x就是描述热机的一些宏观变量（如气缸的压强、体积、温度等等），热机的工作就看作是该系统的演化规律f。按照上一章的讨论，我们希望找到一个状态的函数S(x)，使得该函数能够表示系统随时间演化的总趋势。

让我们先就卡诺理想热机来讨论。我们知道卡诺热机的工作是循环往复的，这意味着当热机从初始状态x₁出发，经过吸热、放热循环之后到了状态x₂，那么这两个状态必须相同才保证系统能够循环往复：x₁=x₂，所以它们对应的S数值也应该相同，即S(x₂)=S(x₁)，这也意味着系统从状态x₁变到状态x₂，ΔS=0。这是对S的基本要求。

另一方面，我们又知道卡诺热机的机械效率定义为(Q₁-Q₂)/Q₁，它等于(T₁-T₂)/T₁，即：

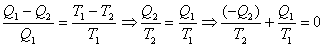（1）

我们看到，在最后一个等式中，每一项都写成了Q/T的形式，如果规定热机吸热为正，放热为负的话，那么最后一个等式就具有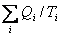的形式（i=1,2）。而该等式告诉我们这个和式为0，这个量刚好满足上面所说的对于ΔS函数的要求，因此克劳修斯猜，也许这恰恰是对熵变的一个定义：

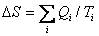（2）

其中i表示整个可逆循环过程中的第i个小过程（可以设想可逆循环通过很多个小的步骤完成）。Q_i表示这个小过程中吸收的热量，T_i则表示这个小过程中系统的温度。假如卡诺热机所经历的小过程（可逆的）无限多，每个小过程又是无限缓慢，我们就可以定义状态函数熵的小变化为：

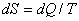（3）

其中dQ为小过程吸收的热量，而dS为小过程中的熵变。（2）和（3）是等价的表达方法，只不过（3）表达的是每个小过程的熵变，它蕴含了（2）即整个过程的熵变。当整个过程是循环的时候，熵变就刚好为0。实际上，（2）和（3）并没有直接给出状态函数熵S(x)或熵变函数具体是什么样子，而是给出了度量熵变化的一种间接方法，即用可逆过程中的dQ/T来计算它，所以（2）和（3）也叫做熵变的定义式。根据该式，如果温度保持不变，那么熵变化的数值和系统吸收的热量就成正比。吸收热量会让熵增加；放出热量熵就减少。因为热是一种不能被系统利用来做功的能量，所以熵变也就度量了系统做功能力的损失或者不可做功的能力的增加。熵的增加和温度密切相关，即温度越高吸收同样的热量，其熵增加也越小，且反之亦然。

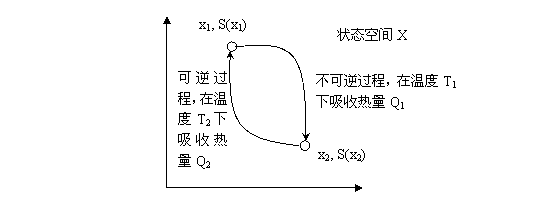图4.4 由一个不可逆过程和可逆过程组合形成的不可逆循环过程

下面再来考虑不可逆过程。假设系统经历一个不可逆过程从状态x₁变到了x₂，那么我们是否还可以运用（2）和（3）式来计算x₁到x₂的熵变呢？为了回答这个问题，让我们设计这样一台特殊的热机（如图4.4）：当热机在高温热源T₁吸热Q₁的时候，系统经历一条不可逆路径从状态x₁变到状态x₂，而当热机在低温热源T₂放热Q₂的时候，该热机进行可逆的变化从状态x₂变到x₁。这样，对热机的可逆过程部分我们可以定义熵变，即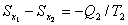：，而总过程显然是不可逆的，所以它的效率一定小于相同温差下的可逆热机效率，所以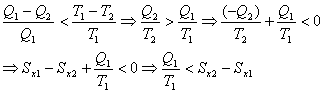：（4）

即对于一个不可逆过程，系统总的熵变要大于系统吸收的热量除以温度。同样，如果不可逆过程由无限多个小过程构成，那么对于每一个小过程，我们有：

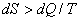（5）

对于不可逆过程，等式（3）并不成立，取而代之的是不等式（5）。所以综合这两种情况，对于大自然的任何一种自然变化过程（无非就是可逆和不可逆两种）来说，

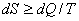（6）

这说明，如果系统吸热，那么它的熵就增加，这个熵增加的最小值是dQ/T。

对于一个孤立系统（不与外界进行能量与物质的交换的系统）来说，因为系统没有从外界吸收热量，所以dQ=0，这就导致了：

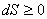（7）

即孤立系统总是要熵增加的，这便是克劳修斯表述的热力学第二定律, 也是第二定律的数学表达形式！克劳修斯的确找到了一个系统的状态函数S，它随时间的变化类似于图3.3（b）所示的情况。因此我们也可以说，对于任意的孤立系统来说，它都有一个目的：让熵趋向最大化。

可以说，热力学第二定律是物理中的一个新的“公理”，因为我们在牛顿力学框架中根本找不到它的影子。但是不可逆的宏观现象逼迫我们必须提出新的公理来解释它们。这样，被牛顿力学模型中“理想化”掉的那些因素，如摩擦、阻力等等又重新被纳入到了热力学第二定律中。克劳修斯的最大贡献在于找到了一种状态变量：熵来模型化热力学第二定律，并且它给熵找到了一种间接的度量方法。打开的香水会挥发到整个房间、破碎的镜子不能重圆，热量不能自发从低温流向高温，所有这些时间不可逆现象都归结于热力学第二定律，它告诉我们孤立系统的唯一目的就是使熵获得增加，这一论述构成了所有不可逆现象的原型。

编辑：wangting