幂律分布背后的数学逻辑,了解一下?
今天我们将带大家来学习一个基本的概念,就是幂律分布的函数形式。这部分的知识来自于集智百科,集智百科是复杂系统领域的百科全书,涵盖复杂系统领域的基本概念。(目前正在不断的完善阶段)
我们正在组织撰写翻译相应的维基词条,并附上代码实现。想要自己创建词条,一起贡献知识的小伙伴们可以通过链接报名哦。点击「编辑」,做些改变,按下「保存」,你将影响世界!
幂律函数
(Power-Law Fuctions)
科学家对幂律关系感兴趣,部分是因为某些机制服从幂律关系所展示出的简洁性。通过研究幂律把握这些机制,不仅了解到一些自然现象的基础,还可以从中窥探出与其他看似不相关的一些系统之间的深层联系;参见前文的普适性。
物理世界中幂律关系无处不在, 部分是由于维度的限制;而在复杂系统中, 幂律通常被认为是层级或特定随机过程的特征。帕累托的收入分配定律,分形的结构自相似性, 以及生物系统中的克莱伯定律,都是比较著名的幂律分布实例。
研究幂律关系的生成, 并致力于在现实世界中对它进行观察和验证, 是物理学、计算机科学、语言学、地球物理、神经科学、社会学、经济学等许多领域研究的一个热门话题。
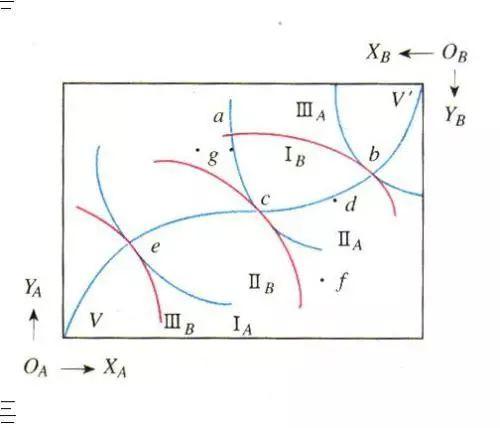
帕累托收入分配定律 | 来源:https://www.google.com
最近对幂律的兴趣主要来自于对概率分布的研究:似乎有大量的分布遵循幂律的形式,至少它们右尾是符合的。这些大型事件的行为将这些数量与大偏差理论(theory of large deviations)的研究联系起来(也称为极值理论(extreme value theory)),它探究了诸如股市崩盘和大型自然灾害等极其罕见的事件的发生频率。在统计分布的研究中更倾向于称之为“幂律”。
在实际情况中,近似为幂律分布的情况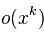 通常包括一个偏差项,它可以表示观察到的值
通常包括一个偏差项,它可以表示观察到的值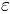 的不确定性(可能是测量或抽样误差),或者提供一种简单的方法使观察偏离幂律函数(可能是因为随机):
的不确定性(可能是测量或抽样误差),或者提供一种简单的方法使观察偏离幂律函数(可能是因为随机):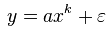
从数学角度来说,一个严格的幂律函数不可能是概率分布: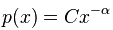 ,对于
,对于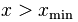 ,指数
,指数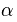 (希腊字母alpha,注意不要与之前使用的指数符号混淆)大于1(否则尾部具有无限区域), ,最小值
(希腊字母alpha,注意不要与之前使用的指数符号混淆)大于1(否则尾部具有无限区域), ,最小值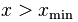 是必须存在的。否则,当x接近0时, 分布就具有无限面积, 常量因子C是一个标度因子, 以确保总面积为 1, 这是概率分布的基本要求。
是必须存在的。否则,当x接近0时, 分布就具有无限面积, 常量因子C是一个标度因子, 以确保总面积为 1, 这是概率分布的基本要求。
更常见的是渐近幂律——只在极限情况下成立。指数通常在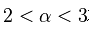 之间,不过这并不绝对。详细信息请参阅下面的幂律概率分布(power-law probability distributions )。
之间,不过这并不绝对。详细信息请参阅下面的幂律概率分布(power-law probability distributions )。
示例
从物理学(例如沙堆雪崩),生物学(例如物种灭绝和体重)以及社会科学(例如城市规模和收入)领域的研究中,目前已经探讨了超过一百种幂律分布。其中包括:气溶胶光学中的Angstrom指数、复杂介质中声衰减的频率依赖性、心理物理学中的Stevens幂律、斯蒂芬–玻耳兹曼定律(The Stefan–Boltzmann law)等等,下面就简单介绍三个应用最广泛的示例。
克莱伯定律(Kleiber’s Law)
在1932年,生物学家克莱伯做了一组实验,他将各种哺乳动物拉到称上称体重作为横坐标,大到几顿重的大象,小到几十克的耗子,然后通过它们在单位时间内呼出的二氧化碳,分别测量出它们的新陈代谢率作为纵坐标。
得出的结果让他大吃一惊。当横纵坐标分别取对数之后,所有的动物都齐刷刷地站在了一条直线上,这条直线的斜率为3/4。生物的多样性令人叹为观止,可竟然出现了在数学上如此统一的规律。
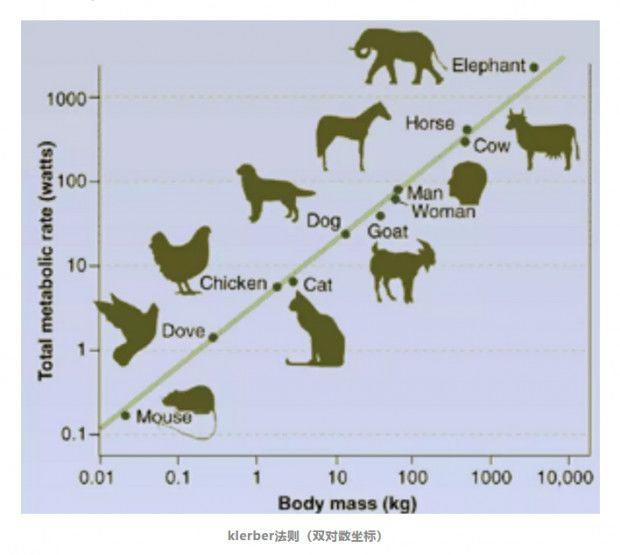
这就是克莱伯定律(Kleiber’s law):对于哺乳动物,其基础代谢率与体重的3/4次幂成正比即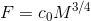 。
。
想了解更多关于克莱伯定律的知识,请看集智学园最美程序媛的作品:
无标度网络模型
早期研究发现在很多网络中,少数节点占据了整个网络中的大部分连边,而多数节点的连边数量很少,节点连边数量的分布符合幂律。以巴拉巴西为代表的科学家们发现了大量满足幂律的网络结构,这种网络被称为无标度网络。人们越来越倾向于认为,幂律(Power Law)是无处不在规律,尤其在复杂网络中。
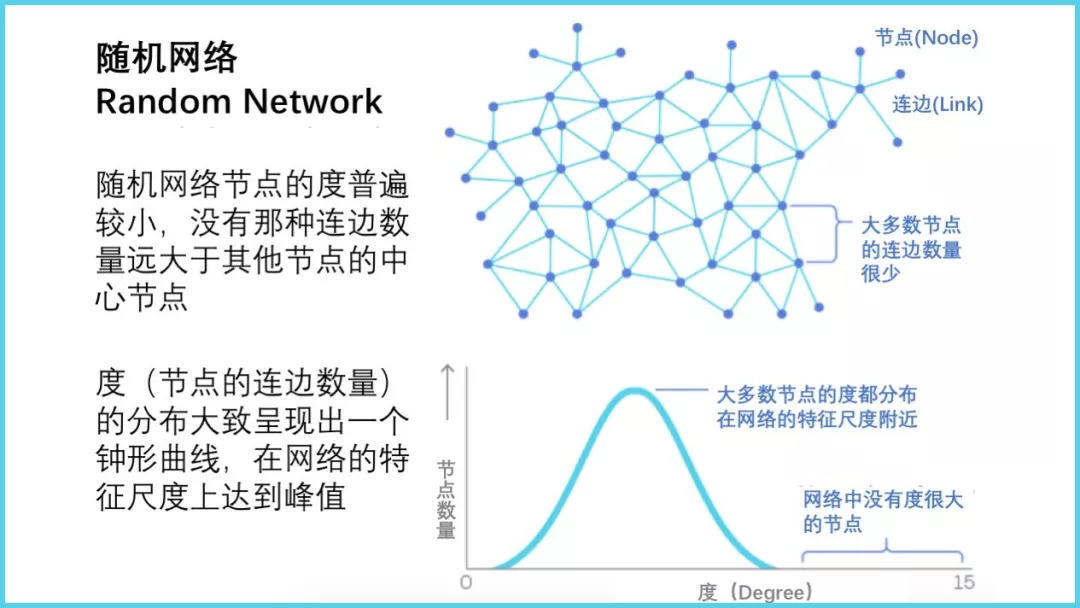
随机网络
想了解更多关于无标度网络模型的知识,请看集智俱乐部往期作品:
Zipf定律:书籍中单词频率的分布
Zipf定律是由哈佛大学的语言学家乔治·金斯利·齐夫(George Kingsley Zipf)于1949年发表的实验定律。它可以表述为:在自然语言的语料库里,一个单词出现的频率与它在频率表里的排名成反比。
所以,频率最高的单词出现的频率大约是出现频率第二位的单词的2倍,而出现频率第二位的单词则是出现频率第四位的单词的2倍。这个定律被视作任何与幂定律概率分布有关机制的参考。
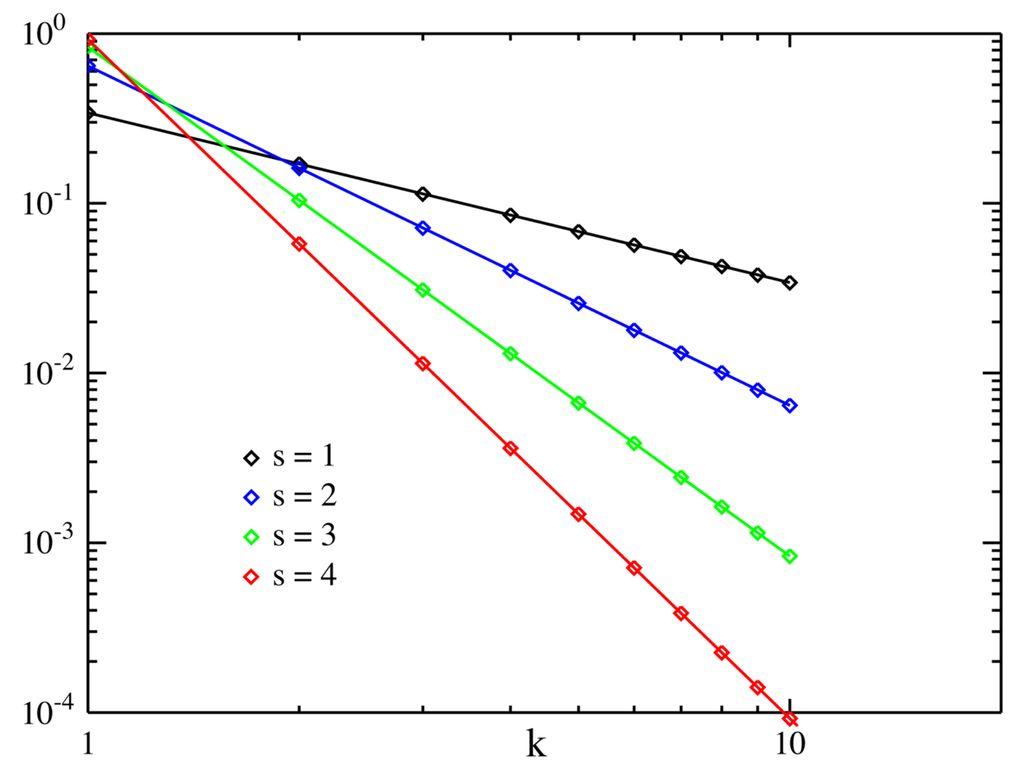
横纵坐标均为对数比例下,齐夫定律的概率质量函数的图像,其中N= 10。横坐标是指数k。(注意,函数仅在k为整数时有定义,图上的连线不代表函数连续。)
其他形式(Variants)
分段幂律(Broken Power law)
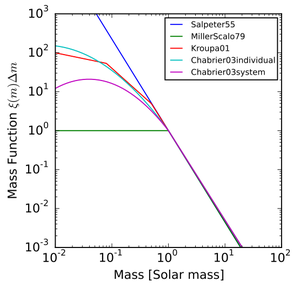
初始质量函数的一些模型遵循分段幂律;Kroupa(2001)红色
分段幂律是一个分段函数,由两个或多个的幂律函数组成,再加上一个阈值。例如,有两个幂律:

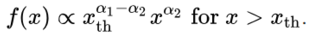
具有指数截止的幂律分布(Power law with exponential cutoff)
具有指数截止的幂律就是幂律乘以一个指数函数:
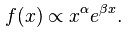
曲线幂律(Curved power law)
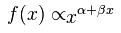
来源:集智百科
地址:
http://wiki.swarma.net/index.php?title=%E5%B9%82%E5%BE%8B%E5%88%86%E5%B8%83&variant=zh-hans
编辑:孟婕
推荐阅读
推荐课程


商务合作及投稿转载|swarma@swarma.org
◆◆◆
搜索公众号:集智俱乐部
加入“没有围墙的研究所”

让苹果砸得更猛烈些吧!
原文始发于微信公众号( 集智俱乐部 ):集智










