检验是否服从幂律分布?2行代码搞定!| 集智百科
本文将介绍如何用极大似然估计、K-S检验和两点拟合法这三种方法,来判断某个分布是否付服从幂律分布。内容来自集智百科,集智百科是复杂系统领域的百科全书,涵盖复杂系统领域的基本概念(持续完善中)。
我们正在组织撰写翻译相应的维基词条,并附上代码实现。想要自己创建词条,一起贡献知识的小伙伴们可以通过链接报名哦。点击「编辑」,做些改变,按下「保存」,你将影响世界!
(Maximum likelihood)
对取自独立同分布的实函数的数据,我们拟合幂律分布的形式: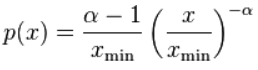
要求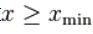 , 其中系数
, 其中系数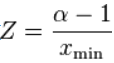 是标准化常量. 给定
是标准化常量. 给定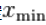 , 则对数似然函数变为:
, 则对数似然函数变为:
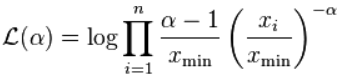
这种可能性的最大值是通过对参数 进行微分来找到的 , 从而使微分等于零,再重新排列,就得到了估计量方程:
进行微分来找到的 , 从而使微分等于零,再重新排列,就得到了估计量方程: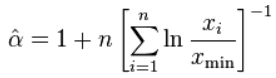
其中 对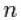 个数据,
个数据,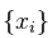 满足
满足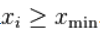 。这个估计展示了一个小范围样本偏差的秩
。这个估计展示了一个小范围样本偏差的秩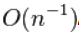 ,当n>100时它会比较小。此外, 这个估计的标准误是
,当n>100时它会比较小。此外, 这个估计的标准误是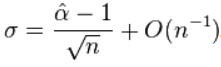 。这个估计量相当于从数量金融学和极端价值理论中获得的需要的 Hill 估计量。对于一组n值的整数数据点
。这个估计量相当于从数量金融学和极端价值理论中获得的需要的 Hill 估计量。对于一组n值的整数数据点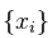 ,对每一个
,对每一个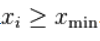 ,都有最大似然指数是先验方程的解:
,都有最大似然指数是先验方程的解: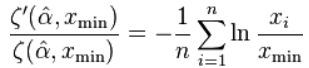
其中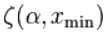 是不完整的黎曼ζ函数。这个估计的不确定性和连续方程的公式是一样的。 然而,这两个方程是不等价的,连续的方程形式不应该应用于离散的数据,反之亦然。
是不完整的黎曼ζ函数。这个估计的不确定性和连续方程的公式是一样的。 然而,这两个方程是不等价的,连续的方程形式不应该应用于离散的数据,反之亦然。
另外,这两种估计都需要选择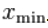 。对于非平凡函数
。对于非平凡函数 , 选择太小的
, 选择太小的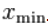 ,
,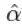 会产生显著的偏误 , 选择过大又会增加
会产生显著的偏误 , 选择过大又会增加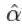 的不确定性, 并且降低模型的统计功效. 所以通常情况下,
的不确定性, 并且降低模型的统计功效. 所以通常情况下,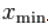 的最佳选择很大程度上取决于左尾的特定形式,以
的最佳选择很大程度上取决于左尾的特定形式,以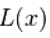 为代表。
为代表。
Kolmogorov-Smirnov估计
另一种计算幂律指数的方法,它不使用独立同分布数据,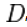 使用的是Kolmogorov-Smirnov统计量的最小值,在数据的累积分布函数和幂律之间:
使用的是Kolmogorov-Smirnov统计量的最小值,在数据的累积分布函数和幂律之间: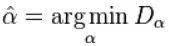
且: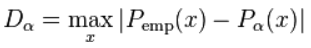
其中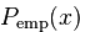 和
和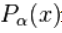 分别表示数据的cdfs和指数的幂律概率分布。由于这种方法不以独立同分布数据为前提,所以它提供了一种替代方法来确定数据集的幂律指数,在这种情况下,时间相关性不能被忽略。
分别表示数据的cdfs和指数的幂律概率分布。由于这种方法不以独立同分布数据为前提,所以它提供了一种替代方法来确定数据集的幂律指数,在这种情况下,时间相关性不能被忽略。
ks检验详细代码如下:
from scipyimport stats
In [41]:
# ks检验
stats.kstest(s, ‘powerlaw’,args=[a])
Out[41]:
KstestResult(statistic=0.01559455659216713, pvalue=0.015442108453260 443)
两点拟合法
(Two-point fitting methond)
两点拟合法可用于无标度分布情况下幂律指数的估计——它比极大似然估计更收敛。研究断裂孔径的概率分布是这种方法的应用之一。某些情况下概率分布并不使用积累分布函数( cumulativedistribution function)表述,而是根据满足X> x条件的X的积累频率(cumulativefrequency),其中X是每单位(或区域单位、秒等)的要素数目,x是一个可变实数。例如,将N个元件的样品的裂缝孔X的累积分布定义为“每米的裂缝数目大于x的裂缝的数目”。使用累积频率有其优势,例如,它允许人们把从不同标度的不同长度的样本线(例如分别从露头(outcrop)和从显微镜)收集的相同的图表数据放在一起。
验证幂律
尽管幂律关系因许多理论原因而具有吸引力,但证明数据确实遵循幂律关系需要的不仅仅是简单地将特定模型拟合到数据中。这对于理解产生分布的机制很重要:表面上类似的分布可能由于显着不同的原因而出现,并且不同的模型产生不同的预测,例如外推法。
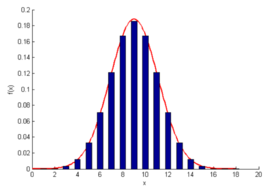
正态分布 | https://baike.baidu.com
例如,对数正态分布常被误认为幂律分布:从对数正态分布绘制的数据集对于大值(对应于对数正态的上尾接近幂律)将近似为线性,但对于较小的值,对数正态将显着下降(向下弯曲),对应于对数正态的较低尾部较小(很少有小值,而不是幂律中的许多小值)。
幂律分布 | 来源:http://image.baidu.com
例如,Gibrat关于比例增长过程的定律产生对数正态分布,尽管它们的双对数图在有限范围内看起来是线性的。对此的解释是,虽然对数正态密度函数的对数在log(x)中是二次的,但在双对数图中产生“弓形”形状,如果二次项相对于线性项较小则结果可以看起来几乎是线性的,并且对数正态行为仅在二次项占优势时才可见,这可能需要更多的数据。因此,向下略微“弯曲”的双对数图可以反映对数正态分布——而不是幂律。
一般而言,许多替代函数形式在某种程度上似乎遵循幂律形式。Stumpf提出在双对数域中绘制经验累积分布函数,并声称候选幂律至少应涵盖两个数量级。此外,研究人员通常不得不面对决定现实概率分布是否遵循幂律的问题。作为解决这个问题的方法,Diaz提出了一种基于随机样本的图形方法,允许在不同类型的尾部行为之间进行视觉辨别。该方法使用残余分位数函数的束,也称为百分位剩余寿命函数,其表征许多不同类型的分布尾部,包括重尾和非重尾。然而,Stumpf声称需要统计和理论背景,以支持驱动数据生成过程的基础机制中的幂律。
验证幂律关系的一种方法是对特定的生成机制对数据进行许多正交的预测。简单地将幂律关系与特定类型的数据相匹配并不被认为是一种合理的方法。因此,在现代科学的许多领域中,对幂律的验证仍然是一个非常活跃的研究领域。
来源:集智百科
地址:
http://wiki.swarma.net/index.php?title=%E5%B9%82%E5%BE%8B%E5%88%86%E5%B8%83&variant=zh-hans
编辑:孟婕
推荐阅读
推荐课程


商务合作及投稿转载|swarma@swarma.org
◆◆◆
搜索公众号:集智俱乐部
加入“没有围墙的研究所”

让苹果砸得更猛烈些吧!
原文始发于微信公众号( 集智俱乐部 ):集智










