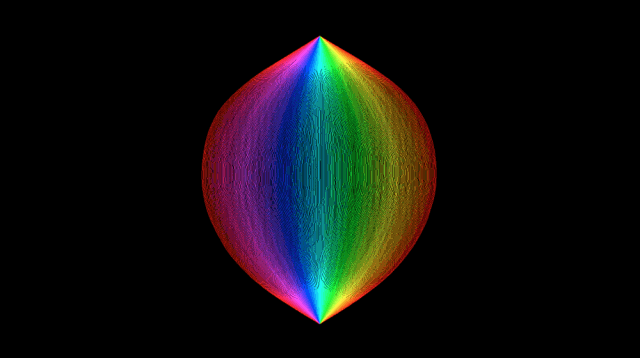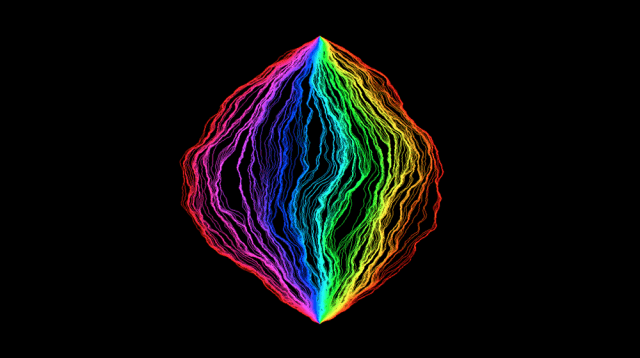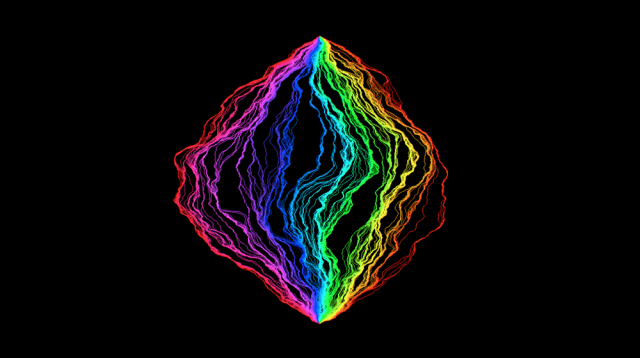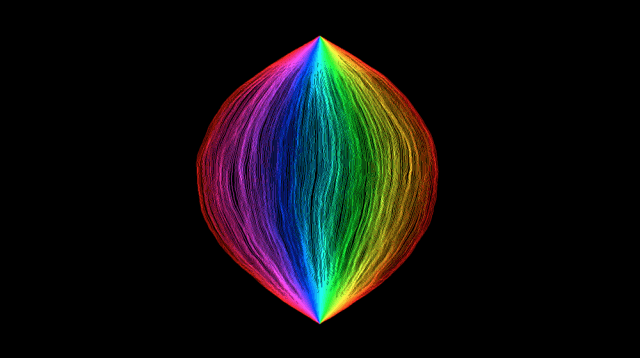
在“SLE曲线”结构中，随机性增加 | 来源：Jason Miller

标准几何体能够用简单规则描述，比如通过y = ax + b定义每条直线，而且各要素之间的关系也相对明了：两点成线，四边成面，六面结合为立方体。

然而，困扰麻省理工学院数学教授Scott Sheffield的不是标准几何体，而具有随机性的形状。因为无法预测路径，世界上不存在两个一模一样的随机形状。最常见的随机形状是随机游走（random walk），从金融资产价格的变动到量子物理中的粒子路径，我们称之为随机游走，因依靠过去的路径，你根本无法预判粒子将来的走势。

Scott Sheffield麻省理工学院数学教授

除了一维的随机游走，还存在随机二维曲面（two-dimensionalsurface）、随机增长（random growth）模型等其他类型的随机形状，比如随机增长模型可以估测青苔在岩石上的蔓延方式。直到现在，数学家仍不能解释这些物理世界中的随机形状，也找不到随机路径和随机二维形状的共同联系。

近年，Sheffield和与其频繁合作的Jason Miller教授（目前在剑桥大学数据实验室任职），发现随机形状之间的相似特征，而且某几类随机物体之间存在惊人清晰的关联——他们的研究开启了几何随机性的统一理论。

Jason Miller剑桥大学数据实验室教授

在接下来的数月中，Sheffield和Miller将会发表三篇系列论文中的最后一部分（介于本报道撰写于2016年，提到的论文已经被发表），首次提出不同于平面的欧几里得映射（Euclidean mapping of the plane），在随机二维曲面上物理与数学随机几何的统一观点。

相关论文：

Liouville quantum gravity and the Brownian map I: The QLE(8/3,0) metric.

https://arxiv.org/abs/1507.00719

Liouville quantum gravity and the Brownian map II: geodesics and continuity of the embedding：geodesics and continuity of the embedding.

https://arxiv.org/abs/1605.03563

Liouville quantum gravity and the Brownian map III: the conformal structure is determined.

https://arxiv.org/abs/1608.05391

量子弦（quantum string）上的

随机游走

标准欧几里得几何，即欧式几何（Euclidean geometry）的研究对象包括：线，射线，以及圆和抛物线这样的平滑曲线，点的坐标值可被清晰、有序的规则，即函数表示。比如，已知一条直线上的两点，就能够推得该直线上的其他点的坐标。该规则同样适用于下图上的每条射线（从一个点向外辐射）。

从中心点向外辐射的线来源：Scott Sheffield

飞机航线可以帮助理解随机二维几何。当一架飞机长距离飞行，例如从东京飞到纽约，飞行员会沿直线从一城市飞向另一城市。但是，如果把航线画在地图上，即，把球体（地球）上的直线映射到一张扁平的纸上，航线会变成弧形。

如果地球不是圆的，而是以随机的方式扭曲而成的复杂形状，二维扁平地图上的航线可能会更加无规律，就像下图中的射线。

地面随机度低时的飞机航线示意来源：Scott Sheffield

每条射线代表从起点出发的航线，在随机波动的几何面中尽量“直线”飞行（意为在表面上从一点到另一点之间距离最近的路径）。随机量的特征如下图所示，笔直的射线因随机量增加而扭曲，出现越来越多几乎不连贯的（incoherent）的锯齿状闪电。

地面随机度增加时的飞机航线示意来源：Scott Sheffield

但是，不连贯不等于不可理解。在随机几何中，如果你知道一些点的位置，在最佳情况下就能推测其余点的分布概率。就像灌铅骰子的点数依然是随机的，但是与均匀骰子不同，可能有不同的分布概率。

地面随机度极高时的飞机航线示意来源：Scott Sheffield

数学家已经发现并且希望继续发现随机几何的概率分布，该分布是特殊的，而且很多领域的研究都涉及到这种随机的几何形状，如果物理学家能够用足够严谨的数学语言描述它们，很多研究都会变得更加顺利。自然似乎倾向于用不可数无限面的骰子生成随机曲面（random surfaces）。像Sheffield和Miller这样的数学家试图研究这种骰子的特性（以及随机几何生成形状的“典型”特性），希望达到我们了解普通球体一样准确。

可通过这种方式进行理解的第一个案例是随机游走。理论上，如果反复掷骰子（正面/反面），生成的“路径”就是一维的随机游走。20世纪20年代，麻省理工的Norbert Wiener用数学将这一过程精准描述为布朗运动（Brownian motion）。布朗运动是随机游走的“尺度极限”（scaling limit），意思是如果随机游走每一步的“步长”和时间间隔都非常小，表现就越来越接近布朗运动。随着时间的流逝，几乎所有随机游走都会收敛为布朗运动。

同时，在物理学家试图理解宇宙结构的时候，他们一次注意到了二维随机空间。

弦理论中，极小的弦（string）随着时间流逝而震动、演化。一个点随着时间变化产生的轨迹会形成一条一维曲线，弦在时空上扫过的二维轨迹可被理解为二维曲面，称为世界面（worldsheet），编码了一维弦在一段时空内震动的历史信息。

Sheffield总结：“要弄懂量子物理的弦理论，你首先需要理解曲面中的布朗运动。”

多年来，物理学家得到一些至少部分相关的成果。20世纪80年代，现在在普林斯顿大学任职的物理学家Alexander Polyakov提出一种描述这些物理学中至关重要曲面的方法，这个方法被称作Liouville量子引力（Liouville quantum gravity，缩写为LQG），虽然并不完善，但是这种看待随机二维曲面的方法依然很有用，作为一个有用的工具，LQG让物理学家可以定义曲面角度，从而，曲面的面积就能计算了。

同样的，布朗地图（Brownian map）提供了研究随机二维曲面的另一种方法。通过LQG可以计算面积，通过布朗地图则可以计算随机曲面上点之间的距离。二者共同为物理学家和数学家提供了互补的视角。他们希望这两种方法是等价的，因为【为什么希望这两种方法是等价的？等价之后有多大用？】但是无法证明这点。

自2013年起，Sheffield和Miller开始着手证明这两种模型的等价性。

随机增长（Random Growth）

为了证明LQG和布朗地图是随机二维平面的等价模型，Sheffield和Miller采用一种理论上足够简单明了的方式。他们希望找到一种LQG曲面的距离度量方式，然后证明它和布朗地图中的距离测量方式是一模一样的。

当开始定义这种新的度量方式的时候他们发现，由于随机曲面太过扭曲，无法在避免撕裂物体的情况下移动笔直的物体。Sheffield和Miller意识到传统定义距离的方法无法实现LQG曲面的距离度量。

因此，二人组把试图重新用关于增长的问题来解释距离。打个比方，曲面上的菌落繁殖，菌落首先占据了一个点，随着时间的流逝，菌落扩张到曲面的任何一个角落。因此，就可以通过菌落从一点扩张到另一点的时间，来测量两点间的距离。Sheffield表示这种技巧一定程度上“描述了球状扩大的过程”。

因为所有点和增长率都是已知且固定的，所以增长过程也是确定的。我们很容易在普通的平面上描述一个球形的增长。随机增长要难得多，很长一段时间困扰着数学家们。但是，Sheffield和Miller很快发现，相比平滑曲面，在随机曲面上运行随机增长模型出人意料得更容易理解，这它们实际上是用相似的数学方法被描述的。Sheffield发现：“在随机曲面上添加增长模型很疯狂，但是某种程度上计算其实更容易了”。

下图展示了一个特殊的随机增长模型，伊甸园模型（Eden model），描述了菌落的随机增长。菌落一边生长，一边在群落的边缘随机生成障碍。任何时候都无法预测下一个障碍的出现地点。通过这些图像，Sheffield和Miller展现了伊甸园模型在随机二维曲面上的增长模式。

第一张图表现了在相当平坦（随机度低）的LQG曲面上，伊甸园模型逐渐增长，形状接近同心圆，颜色代表曲面的不同时间随机增长能接触到的位置（见下图）。

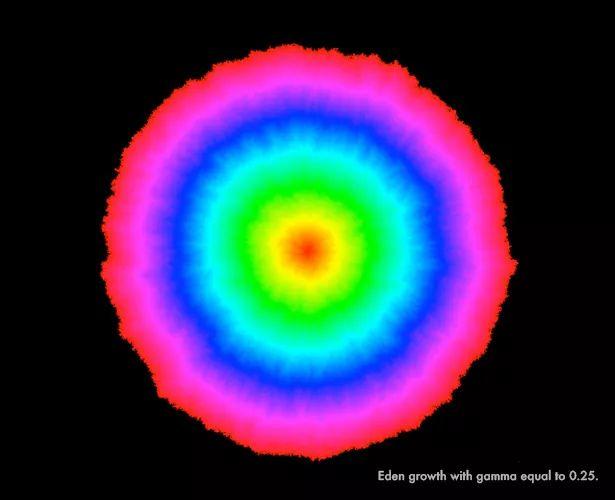
gamma为0.25 时随机增长模型的形状示意来源：Jason Miller

Sheffield和Miller在后续几张图片展现了越来越随机的曲面增长。生成曲面的函数的随机度由常数gamma控制。当gamma增长，曲面的高峰低谷愈发明显，曲面的随机增长同样更加无规律。上一张图的gamma为0.25，下图的gamma为1.25，曲面构建的随机度是前者的5倍。高随机性的曲面的伊甸模型同样是扭曲的。

gamma为1.25时随机增长模型的形状示意来源：Jason Miller

当gamma为8/3（三分之八）的平方根（大约1.63），LQG曲面波动得更加剧烈，呈现了和布朗地图相匹配的粗度，因此可以直接比较两模型的随机集合曲面。

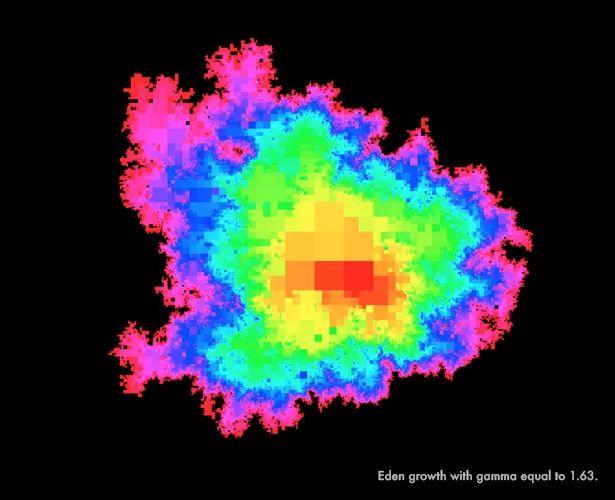
gamma为8/3（三分之八）的平方根时随机增长模型的形状示意来源：Jason Miller

这样粗度的曲面的随机增长非常不规律，试图用数学方法描述他就好像试图预测飓风中微小的气压波动，是不现实的。Sheffield指出：“很难给出随机增长的精确数学表述，这需要一些惊人的巧妙方法。他们意识到，他们需要在随机度很高的LQG曲面上模拟伊甸园增长，建立一个与高随机度布朗地图相等的距离结构（distance structure）。

他们最终引入了一个巧妙的数学工具解决了这个问题。

随机探索

Sheffield和Miller的巧妙方法利用了一种特殊的一维随机曲线，它很像随机游走，唯一区别就是它不与历史路径交叉。物理学家在很长一段时间都面对着这种曲线，比如正旋或反旋的粒子群的边界（具有一维路径而且形状随机不交叉）。就像Robert Brown在自然界观察到随机交叉路径一样，他们在自然界发现了这种随机、不交叉的路径，但是他们无法以严格的方式研究这种路径。1999年，那时还在微软研究院的Oded Schramm证明了SLE曲线（Schramm-Loewner evolution）作为非交叉随机曲线的一个权威标准。

图：SLE曲线的一个案例来源：Jason Miller

Schramm对SLE曲线的研究是随机物体研究中的里程碑。普遍认为，如果Schramm提前几周发表研究，他就能获得菲尔兹奖。然而，Schramm在2008年徒步旅行中意外丧生，Wendelin Werner（2006年）和Stanislav Smirnov（2010年）却先后在他的研究基础上获得了菲尔兹奖。更重要的是，SLE曲线可以证明许多随机物体的其他特性。

注：菲尔兹奖只颁给年龄不超过40岁的数学家。

Sheffield是Schramm的朋友和合作者：“Schramm的发现让很多物理学中确信可以用物理的方式证明的东西，终于能在数学层面进行严谨验证。”

在证明LQG和布朗地图等价这一问题中，Sheffield和Miller就以一种意想不到的方式继续发掘了SLE曲线的价值。为了证明LQG曲面和布朗地图是等价的，需要衡量LQG曲面上的距离，然后由此证明LQG曲面和布朗地图是等价的。他们得想办法在随机曲面上模拟随机增长。SLE就是他们想到的办法。

gamma控制LQG曲面的粗糙程度，SLE曲线中也有一个起到类似作用的常数kappa，它则控制SLE曲线的“扰动”。当kappa较低时，SLE曲线看起来就像直线；kappa增长，意味着在不能交叉的条件下，曲线变得更加不规则。下图为kappa为0.5的SLE曲线和kappa为3的SLE曲线。

kappa为0.5的SLE曲线来源：Scott Sheffield

Sheffield和Miller注意到，如果kappa设为6且gamma设为8/3的平方根，随机曲面上的SLE曲线遵循一种探索历程。基于Schramm和Smirnov的研究，Sheffield和Miller发现，当kappa为6时，SLE曲线遵循一种仿佛“盲目的探险家”的轨迹，她会构建走过的路径。如果发现碰到了走过的路径，她就换一个方向，避免路径交叉或死胡同；其他时候则随机走动。

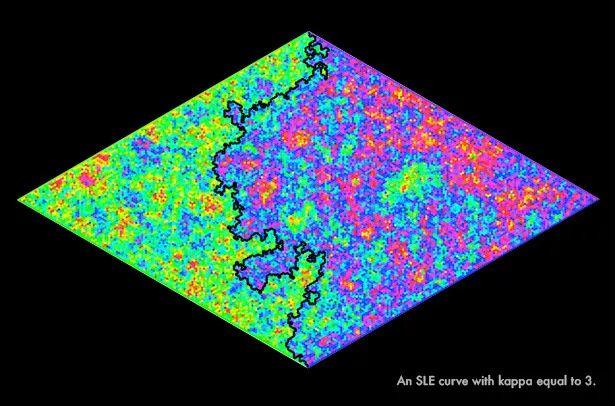
kappa为3的SLE曲线来源：Scott Sheffield

Sheffield说：“‘探险家’每次碰上走过的路径，都会切断一部分被路径完全包围的区域。”

Sheffield和Miller研究了伊甸园模型（类似细菌生长），二者在随机曲面上存在类似的效果：通过“切断”一部分未勘探区域来增长。在菌落模型和探险者模型中，切断的区域看起来一模一样。而且，无论什么时候，探险者模型和菌落模型的随机曲面的未勘探区域信息都是等同的，这也就由此证明这这条分割了区域的曲线长度就是从某点到另一点的”距离”。

在2013年发表的一篇文章中，Sheffield和Miller假设，如果一个失明的人（随机运动的人）可以神奇的被随机送到一个在她曾经到达的区域边界上的一个新的点，每隔一段时间观察后，再做一次这样的操作，看看会发生什么。随着她在边界点上移动，她从所有边界点出发的路径都会不断地效增多。如果给出足够的时间让她去探索，形成的路径就会类似于伊甸模型，即随机增长模型。如此，SLE模型的这种特殊形式就能妙得描述随机增长过程。Sheffield表示：“SLE曲线和随机增长之间的关系很特殊，在那一瞬间，所有问题都能被解释了。”

通过使用随机增长模型来在LQG曲面上定义的这个距离结构，最终被证明与布朗地图中的距离所一致。最终，Sheffield和Miller将数学与物理领域描述二维曲面的模型融合为一个统一的，数学概念上被完整理解的基本对象，实现了理论统一。

利用随机性

Sheffield和Miller已经在arxiv.org发表了证明LQG曲面和布朗地图等价性的前两篇论文；他们已经于16年八月发表表系列的第三篇，讨论不同随机形状（随机不交叉曲线，随机增长，随机二维曲面）和过程间的相似和关联处，表现了随机几何学研究中越来越高的复杂性。

Sheffield形容说：“就好像身处有三座不同洞穴的山里。一座是铁的，一座是金的，一座是铜的。突然，你发现了一条联通三个洞穴的小路，然后三条路就变成了一条路。”

还有很多开放性问题没有得到解答，比如，较这篇论文精细的LQG曲面中，SLE曲线、随机增长模型和距离测量之间的关系是否依旧成立。从实践方面看，Sheffield和Miller的发现可以用来描述真实现象的随机增长，比如洞穴中的雪花、矿物的形状和神经元的树突，但只限于随机曲面条件下。我们仍然不知道，他们的方法是否可以应用在普通欧几里德平面上，也就是我们的现实空间。

翻译：Elena

审校：陈曦、Vera zoo

编辑：王怡蔺

原文地址：

https://www.quantamagazine.org/a-unified-theory-of-randomness-20160802/?utm_content=bufferb2850&utm_medium=social&utm_source=facebook.com&utm_campaign=buffer