尽管大数据的收集越来越容易,但随着从微观到宏观的尺度(scale)变化,系统行为会发生非线性的变化,这让模型构建、行为预测困难重重。如何跨越系统的尺度变化,挖掘出对系统行为真正起到影响的重要信息,是复杂系统研究成败的关键。
美国新英格兰复杂系统研究所(New England Complex Systems Institute, NECSI)的 Yaneer Bar-Yam(创始人及所长)在 2016 年撰写了这篇综述,梳理了重整化群、临界相变、复杂度曲线、混沌等多尺度分析方法,并以生物进化、多样性、种族暴力、市场价格波动等具体问题做了分析,尝试总结出一套复杂系统跨尺度研究的通用框架。
From Big Data To Important Information
https://necsi.edu/from-big-data-to-important-information
人类一直在利用科学上的进步寻找新的机会来收集大量关于复杂系统的数据。虽然在系统的精细映射方面取得了关键进展,但如何将这些数据与解决人类面临的许多挑战相联系尚不清楚。我们往往希望能够通过确定干预措施对系统的影响来解决问题,但这种影响并不会明显地表现在可用的详细数据中。在本文,我们回顾了一些相关的关键概念,并试图构架一个通用框架,用于建立复杂系统的大尺度视图,以及刻画信息在物理、生物和社会系统中的重要性。我们会举例说明它在(与生态、生物多样性、流行病和人类寿命等方面有关的)进化生物学中的应用,以及在种族暴力、全球粮食价格和股市恐慌等社会系统方面的应用。科学探究就是努力确定什么是重要的什么是不重要的,这样才能增进我们对许多实际问题的理解和解决,诸如经济发展、疾病防治等。
治疗疾病和扭转不稳定增长的经济都是人类当前面临的众多复杂挑战中的项目。我们该如何利用日益增多的可用海量数据来解决这些亟待解决的问题?这些数据提供了丰富的细节,但是通常没有标签来标识哪些信息可以关键性地确定出有效干预措施。我们需要解决的问题是关于诸如人体生理、全球经济这样的复杂系统的属性。要解决关于这些复杂系统的问题,需要厘清其中错综复杂的依存关系和行为的多重因果联系,并充分认识到系统行为会跨越微观到宏观的多个层次。
我们认为解决这些问题的关键是关注行为在不同尺度上的关联方式,以及系统内部的依存关系如何引致大尺度的行为模式,这些大尺度的行为模式可以被直接刻画,而不需要映射所有错综复杂的细节。该方法建立在对如何聚合组元行为以识别更大尺度行为的理解之上,这个方法由物理学相变中”重整化群“的研究中发展而来,并被推广到多尺度信息理论。在这个框架中,信息本身是有尺度的,大尺度信息是需要知道的最重要的信息,逐步更精细尺度的信息只是在必要时提供细节。这种分析将重点放在刻画如何影响系统最大规模行为的那些信息上。在生物系统和社会系统研究中,建立从分子尺度到全局尺度的所有因果映射是徒劳的,而这种方法提供了一条捷径。需要被研究的具体原因和作用只是所有尺度的系统行为中的一小部分。因此,相对于扩展传统方法以获得预期结果的方式,这种方法极其简洁。但是,这种形式化的方法在特定情况下的实际应用仍然具有挑战性。只要运用得当,其分析结果对如何干预和解决重大问题具有明确的指导价值,能确定出高层次的努力方向。一些成功的例子表明,这种方法可以应用于各种各样的科学疑问和现实世界的问题中,虽然如何进行更广泛方面的应用亟待进一步发展。当利益的影响范围跨尺度时,必须采用其他方法。通过该方法的一般形式化描述,就可以理解该方法的优势和局限性。
这种方法是对许多其他应用于复杂系统的研究方法的补充,不仅有大数据,而且还包括网络模型、多主体模型、博弈论、系统动力学、机器学习、随机建模、耦合的微分方程组,以及其他一些起始于特定表示的框架。从关注尺度的作用看,这个方法在精神上很接近于分形和混沌,但它没有采用这些特定的表示方法。本文所描述方法其策略是以最小但可靠的表示来描述最大尺度的行为,每每一个不同的表示方法,或者它们的组合,都可以适当地加以使用。
本文回顾并扩展了系统定量分析的基本方法。虽然许多概念是在物理学中发展起来的,但其具有一般性,可以较好地应用于复杂的生物和社会系统。本文的目的是为了让更多的人能够接触和理解这样的基本见解,这种能力对于那些致力于复杂系统定量理解的物理学家和数学家是极为重要的。尽管我们努力让它容易理解,但本文并不是一个复杂系统科学概念和方法的通用教程,如果要学习这方面的知识请参阅文献材料 [1, 2]。回顾某些基本概念在这里是必要的,因为它们通常不是采用便于泛化的形式给出。本文包含一些在生物系统和社会系统应用的例子,虽然这些例子并没有展示出这个基本方法的全部功力,但都很好展示了其应用于具有实际重要意义的高度复杂的系统的各个方面。如果不提及基本的一般方法,就不容易弄清这些例子是如何被研究的。本文不是告诉“怎么做”,而是提供一个概念性的框架和动机,因此还有很大的空间留给其他文章,由它们来提供对未来工作的实际指导。
在第 II 节,我们回顾了依赖于行为的尺度分离而以微积分和统计学为基础工具的传统科学方法的本质。我们将指出为什么它们对于造成多尺度行为模式的复杂系统的内部依存关系不再有效。在第 III 节,我们描述了一个关于微积分和统计学失效的基本洞察力是如何从物质相变的研究中产生的,这导致了重整化群这种多尺度方法的概念的发展。在第 IV 节,我们通过介绍复杂度曲线(对复杂系统的多尺度刻画)以及在特定尺度上可靠描述的概念,给出了应用于复杂系统的多尺度分析方法的通用形式。第 V 节讨论了在重整化群中形式化的普适性的概念,其适用于多种复杂系统场景,可以用来判断大尺度系统行为特征的重要程度。第 VI 节简要讨论了由于放大、耗散和混沌的动力学而产生的复杂性,这些动力学行为随时间会发生尺度上的变化。第 VII 节简要地讨论了几个例子,包括种群生物学、种族暴力、粮食价格机制、市场崩溃、组织结构以及其他。在最后的第VIII节中,我们指出,如果不关注普适性就不可能有效地理解系统,因为每个观察都是来自于不同的微观状态。因此,将科学探究锚定到那些关注大尺度行为的尺度敏感方法是至关重要的。如果不注意尺度,任何方法都注定会错过系统的核心大尺度特性,而将大部分精力都浪费在无关的精细尺度细节上。
II. 尺度的分离
(SEPARATION OF SCALES)
关于复杂系统的一个核心观点是,传统的数学和概念性方法不能充分表示系统内组元之间依存关系的影响,其局限性的关键在于它们仅适用于那些行为在宏观和微观尺度上存在分离的系统,而复杂系统各个部分之间的相互作用会导致跨尺度的行为而违反了这种分离。
考虑一个块沿斜面滑动的滑块。传统的方法会在微观尺度和宏观尺度下分别处理。为了解决微观尺度下(分子)的动力学问题,我们会对它们进行平均,并使用热动力学描述它们的温度和压力。为了描述宏观尺度下的动力学(斜面上滑块的运动),我们使用牛顿物理学来讨论它们的大尺度运动 (图1)。这个例子中,物体中的各个部分可以被认为要么是相互独立行为的(如微观尺度上的随机相对运动),或相干作用(和宏观尺度上的平均运动一样)。因为这些尺度区别非常明显,有数量级上的差异,所以我们分别描述它们时不会遇到问题。最后,我们通常默认块和斜面的结构都是固定的。
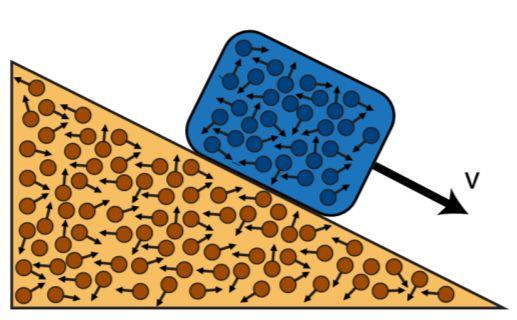
图 1. 滑块 (某时刻速度为 v) 沿斜面滑动的示意图。
受重力和摩擦影响的宏观运动可以用牛顿运动定律来处理,而原子的微观行为可以用热力学来处理,认为原子群的局部振荡是随机和独立的 (一群粒子处于特定状态的概率与另一群的状态无关);对这种运动的统计处理确定滑块和斜面的压强和温度。
因此,传统地看,一个系统具有三个侧面:精细尺度的,动态的,和固定的。桌上放一杯水,里面放一块冰块,可以通过考察冰块的运动和融化情况、分子的平均振动以及玻璃杯的固定结构来处理。在很大的时间尺度上,水终将蒸发,玻璃会流动,桌子可能会腐烂,但是这在一个特定的尺度 (或某个尺度范围) 的观察中并不重要。
考虑从太空看地球这个例子。地球是高度复杂的,但我们仍然可以用可预测的方式将其描述为一颗围绕太阳运行的行星。地球上所发生事情的大部分细节在地球的运行轨道尺度上起不了任何作用。在其轨道尺度上,地球所有的内部结构都可以平均到一个点。假定太阳系中的天体不变,而且每个天体的物质都与其他天体完全分开,我们就可以对这些天体的动态行为进行建模和预测。
当尺度分离起作用时,我们不仅可以描述系统孤立存在的情况,而且还可以描述它对外部作用的反应。如在轨道运动尺度上,作用在地球上的力与在这个尺度上发生的动力学行为是相关联的。如果我们考虑一个新的天体进入太阳系,除非它打乱了系统的结构 (如撞碎一颗行星),只要我们的兴趣还在轨道运动的尺度上,我们就可以用那些相同的自由度来描述系统的行为。
对于复杂的系统,我们最想回答的问题也是与大尺度的信息有关。显然,描述的尺度和交互作用的尺度要是相近的。当我们描述系统大尺度的行为时,我们也会考虑环境对系统在大尺度上的影响,以及系统对环境的反作用。
但是,许多系统,特别是那些我们非常想弄清楚其机理并试图加以影响的系统,并没有很好地在微观和宏观尺度上分开描述。以一群鸟为例,如果所有的鸟都是朝不同的方向独立飞行,那么我们就需要分别描述每一只鸟。但如果它们都朝同一个方向运动,我们就可以简单地只描述它们的平均运动。然而,如果我们对它们的群体行为感兴趣,那么描述每一只鸟的运动信息太多了,而只描述它们的平均运动信息又太少了。复杂系统内部往往既不是完全独立也不是完全相干一致,最好的处理方法是跨尺度的描述。这需要知道哪些信息可以在感兴趣的尺度上被观察到。这个例子的一般化框架可以广泛应用于不同的复杂系统。
III. 理论与实证的矛盾与多尺度洞察力
(THEORY-EXPERIMENT CONTRADICTION AND MULTISCALE INSIGHT)
传统物理学和20世纪70年代起发展起来的以重整化群方法为基础的统计物理之间的差异可以帮我们理解一些关键思想。这种新框架下的建模可以区分出最大尺度上可以观察到的东西。为了解释这种形式化概念,我们叙述它在材料研究 [3-9] 中的发展。然后给出可应用于复杂生物系统和社会系统的一般形式。
在对物质的研究中我们不用具体到到单个原子运动的,而是使用压强、温度和体积来描述我们看到的东西,以及我们可以如何使用力来操纵物质。例如,用活塞压缩气体会减少气体体积而增加压强,热量传递到物体会导致其温度上升。我们能够进行这种描述完全依赖于尺度这一关键概念:原子在精细尺度(微观)的行为对于我们观察和操纵系统并不重要;我们观察和操纵的是大尺度(宏观)性质,它们反映的是原子运动特征的平均或聚合。
这种方法是在19世纪通过统计物理学形成的,它通过最小化与宏观变量有关的自由能来确定平衡态下材料的性质。这种方法几乎总是有效的。然而,在研究水与水蒸汽之间或铁磁体与顺磁体之间的相变时,人们发现这种方法对特殊情况下的二级相变点的性质所给出的结果并不正确。这种现象提供了复杂系统的一个简单示例,在这个复杂系统中,各组元之间既不完全独立又不完全一致,此时尺度分离的特征被破坏。
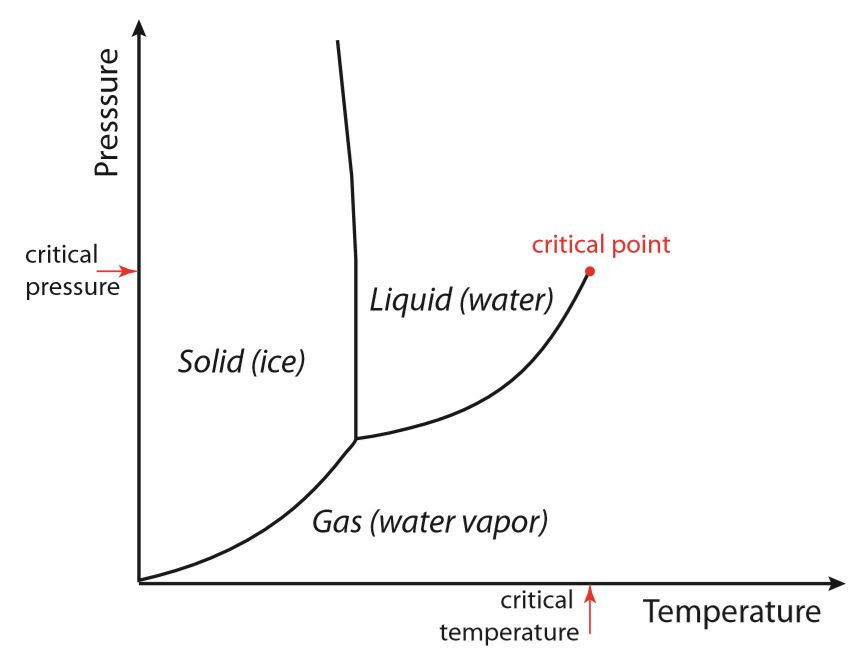
图2:水的相图。液态水和气态水之间的转变停止在临界点(红点)。在临界点,类液体和类气体密度之间的波动存在于整个系统,因此系统不再平滑(违反微积分的假设),平均值失效(违反统计的假设)。为了解决这个问题和其他类似问题,人们发展出一种考虑跨尺度行为的新方法,即重整化群。
考虑水和水蒸汽之间的转变。在一定压强下,我们可以通过提高温度,使水变为蒸汽(液相转为气相)。在转变温度,物质的密度会突然(不连续地)发生变化,这被称为一级相变。若我们增大压强,蒸汽会被压缩,转变点的(液相和气相)密度差异会减小(图2)。到达一个特定压强后这个密度差异就消失了,液态水和气态度水之间不再有区别。这个点被称为二级相变点,它是一级相变线的终点。在二级相变点附近,液相和气相之间的密度的不连续跳跃程度变为零,密度差的变化形式是幂律的ρ ∝ Xβ,其中 x 是沿着一级相变线到二级相变点的距离。还有许多其他材料的相变线也会终止于某个点,这被称为二级相变点或者临界点。在临界点附近幂律规律是普遍存在的。实证研究表明磁体和水的气液相变行为还有其他一些例子的幂律指数是一样的 β ≈ 0.33 [10–12]。然而,基于自由能极小化的理论预测值为0.5 [13],其推导是从临界点密度的自由能解析展开出发,然后将它的导数设为零以得到最小值(朗道理论)。
观测和理论之间的这种巨大差异促使我们的理解发生了重大变化。我们通常使用的微积分和统计学方法在这个临界点上失败了,这是因为它们需要的假设不再成立。微积分假定物质是平滑的,而统计学假定大量对象的平均是明确定义的。在远离临界点时,由于原子的微观行为与整个材料的宏观行为分离得很好,这些假设成立。此时,材料的不同部分看起来本质上是相同的,它是光滑的,对原子属性的任意局部平均会是同样的数值。然而,在临界点,密度的涨落波动(介于类液与类气条件之间)使得物质不再是光滑的,材料的整体平均密度不能代表任何时刻和位置的局部平均密度。在临界点附近,整个材料会由高密度和低密度的区块组成,这种区块状会存在于所有尺度,甚至在宏观尺度。
为了在数学上解决这个问题,人们发展出重整化群[5]。在重整化群方法中,人们认为系统存在多重尺度(分辨率水平)。在某一分辨率水平上宏观密度是随空间变化的,相关的更大尺度的宏观密度应该是采用局部平均而不是全局平均。这种平均将一个观测尺度上的自由能与一个更大尺度上的自由能联系起来。系统的性质可以从行为如何随尺度变化找到,取任意大(甚至无限)尺度为极限。数学计算并不容易,但计算得到的参数与实证发现是相符的 [4,5,10]。自重整化方法发展以来,有关材料结构和动力学问题的探索取得了许多进展[16,17]。
传统方法和重整化群得到的结果是不同的,原因在于,在这种情况下,自由能不是平均密度的函数。尽管如此,我们也没有必要考虑单个原子之间的相互作用。对于液相向气相的转变,自由能取决于密度的空间变化,即不同位置的局部密度如何相互作用。局部密度之间有许多可能的相互作用会对影响自由能。然而,其中只有一部分是重要的。使用重整化群这种方法,可以确定哪些描述相互作用的参数是重要的,而哪些不是。“相关”参数是指随着尺度升高而增大的自由能参数,反之,“不相关”参数随尺度升高而减小。因为物质中有很多原子,所以不相关参数并不会影响物质的宏观变化或在临界点附近我们与物质的相互作用情况。因此,在实际研究中,尽管我们可以微观地测量不相关参数,但由于其并不会影响我们的观察,所以我们只需要考虑相关参数即可。
IV. 表示和信息都是尺度的函数
(REPRESENTATIONS AND INFORMATION AS A FUNCTION OF SCALE)
为什么以微积分和统计学为基础的朗道理论会失败?问题不在于让自由能最小化的目标,而是在于对材料的表示。假设自由能是平均密度的函数是不行的的,因为只有一个变量不能捕捉到材料中正在发生的事情。但另一方面,我们也不必要清楚所有原子的位置,只需要知道密度的空间分布格局。我们越贴近观察,所需要的密度的数值就越多。我们表示系统的方法就是症结所在——在我们选择的系统观测尺度上的表示是否充分。
表示是从系统到数学变量的映射。更准确地说,一个表示应该被理解为系统的可能状态集到数学变量的可能状态的映射。一个忠实的表示必须具有与它所表示的系统相同的状态数,这才可能使得表示的状态可以一对一地映射到系统的状态。如果一个模型的状态比系统少,那么它就不能表达出系统发生的所有事情;如果模型有更多的状态,那么它会表达出系统不可能发生的事情。传统的模型往往没有考虑到这点,就导致了系统和模型的不匹配。这些不可靠的表示无法正确地区分系统的行为,因此也最终无法识别系统对环境外力或我们可能考虑的干预措施的反应。因为我们想对系统施加影响,要知道重要的区别,我们就必须把注意力集中于在那些在特定观测尺度上可以区分的状态。
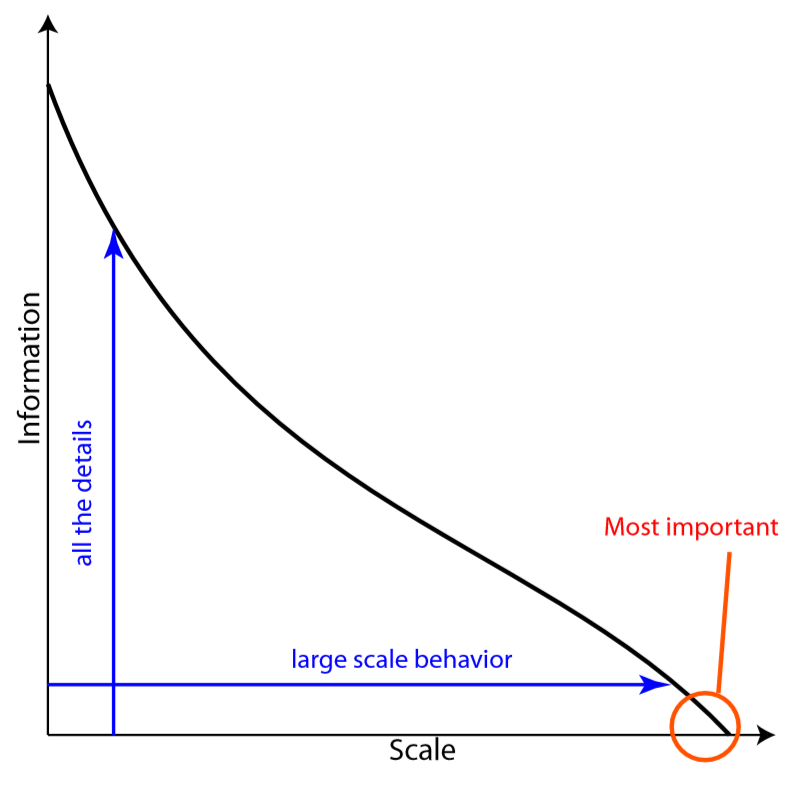
图3:复杂度曲线(尺度的函数)。
复杂度是描述系统所需的信息量,会随着尺度变化而变化。通常,尺度越高(大),所需的细节越少,因此信息量也越少。
为了将这些思想形式化用于复杂系统,需要理解与尺度相关的信息。我们定义了复杂度曲线[1, 14],复杂度是表示一个系统所必需的信息量,它是尺度的函数。信息理论中,一个消息中的信息量是消息的可能数量的对数值(以2为底)。这样,系统在所有特定尺度上的可能状态数就确定了系统的复杂度曲线。通常,对一个系统考察得越精细,描述它所需要的信息量就越大(图3)。因为量子不确定性,系统在最精细尺度上的复杂度也是有限的,等于一个普适常数 1/KBln(2) 乘以系统均衡状态的熵,其中 KB 为玻尔兹曼常数。
单个实数的位数是无限的,有无限多个可能状态,所以它有能力表达一个无限的信息量。这似乎表明我们可以使用一个实数来表示一整个系统。例如,一个表示液体密度的实数,应该可以包含有无穷的信息,但是我们从前面的关于相变的讨论已经知道,单单这一个数值是不够的。为什么不行?问题在于,信息在这个真实数值中按尺度的组织方式与系统中的方式不一致。一个实数可以在一维方向上表示一个点的位置。假设我们从知道物体在1个标准单位长度分辨率下的位置开始。将分辨率增加一倍,就意味着我们可以区分这个位置是在其中的哪个1/2单位长度上。通信此信息需要一个二进制变量。分辨率每增加到2倍,就有2个额外的可能性需要确定。需要的二进制位数是分辨率尺度的对数(以2为底)。然而,对于在其临界点状态的液体,为了描述密度的波动,位数增加不等于分辨率的增加,这个增长要比分辨率加倍的速度要快(见图4)。
图4:一个实数(上面的,x)有无穷的位数,确定一个点的位置,在精度加倍(尺度减半)的情况下,会增加2种(位置的)可能性,信息量增加1。单个实数值并不能很好的表示整个复杂系统,因为复杂系统的信息量不同于尺度增加(y),其位数的增加应类似于图3所表述的复杂度曲线那样。
因此,对系统的一个充分的表示,就是在不同的分辨率下都有一个可能状态集能对应到系统不同状态集,自上而下,直到需要我们去描述的那些我们所关心的性质的层次(相关参数),不用再细。在考虑影响系统大尺度属性(而不是系统的详细细节)的干预时,我们应该从系统行为的最大尺度的模式出发,增加一些需要的补充信息。根据复杂度曲线,关于系统的每一个信息块都有其规模(size)属性——就是我们可以开始检测这个信息块的最大尺度。
因此,更一般的,描述系统的信息是尺度的函数(图3[1])。直观地看,随着尺度的升高,我们需要的信息越来越少。如果信息作为尺度的函数存在高原(plateaus)性状,就有明显的尺度分离情况。而在二级相变时,我们找到一个幂律行为,它是尺度的函数,这个时候没有尺度分离。
物理中使用的重整化群与我们有兴趣研究的复杂系统中的应用方式不同,要通过复杂度曲线形式化。重整化群也是通过系统能量来描述,它大约是最大的“热力学”尺度,即无限规模。但是,在考虑复杂系统的行为时,我们对发生感兴趣行为的系统层次(即人类健康或社会经济活动)更为关注。对于思考这些复杂系统,无限规模并不总是有用的。为了实现我们的目的,我们要识别的系统属性是在特定尺度上表征其动态行为的系统的可区分状态集。
尽管如此,重整化群的方法论带给我们的不只是概念,我们也得到关于如何基于组元的整合识别相关变量构建模型的形式化指导。随着尺度的提升,我们看到的细节越来越少,小的可区分差异消失了,只有涉及系统许多部分的更大的差异仍然存在。部分的特征如何聚合(aggregate)为观察到的(或重要的)总体特征?通过研究这些特征的聚合方式,我们可以识别确定出重要的大尺度系统性质。聚合结果取决于各部分之间的相互依存关系(Aggregation is determined by how the parts depend on each other)。
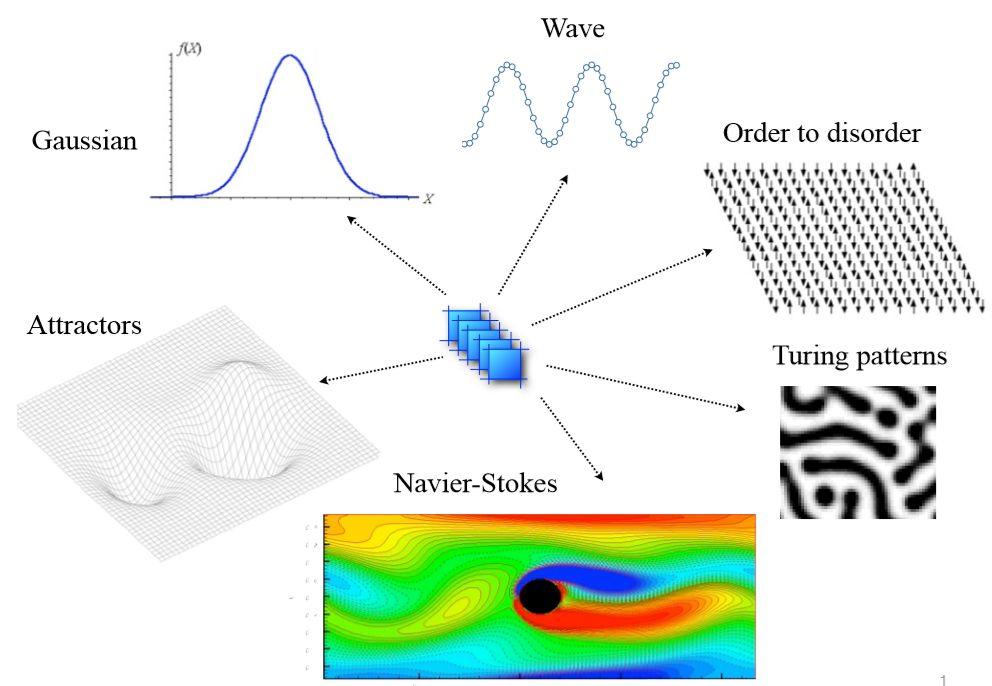
最简单的情况是系统各组元完全独立或完全不独立,在前一种情况下,聚合结果可以从统计学中正态(高斯)分布描述的均值和随机偏差知道,而完全不独立会产生单一的相干行为。当存在下一节要讨论的其他类型的依存关系时,就会发生与上面不同的系统行为,这些行为包括动态振荡和空间模式(图5)。
图5:当我们关注最大尺度时,系统行为会映射到简化的模型上,每个模型都可适用于具有广泛不同的微观细节的大量可能系统。此图显示的一些例子:高斯分布、波动、从有序到无序(如本文讨论的相变)、图灵斑图、Navier-Stokes方程描述的流、吸引子动力学。少数几个模型就可以捕获大量不同系统的行为,其根源是普适性,具体系统是普适性行为类的成员。
V. 普适性、正态分布及更多
(UNIVERSALITY, NORMAL DISTRIBUTIONS AND BEYOND)
当我们研究一个系统的最大尺度行为时,我们可以简化系统的数学描述,因为可区分的状态较少,只有非常有限的行为可能发生。这也意味着在微观尺度上不同的系统在宏观上可能看起来并无不同,因为它们的数学描述变得一样。
一个例子是,液体被加热到沸腾转变为气态和磁铁受热达到某一点使它变成非磁性的(从铁磁到顺磁转变)具有相同的性质。这不是巧合,也不仅仅是类比,而是一种直接的数学关系。磁体具有局部的磁化强度,在磁性临界点处起伏,就像水和蒸气在临界点处的密度一样。正如水分子随着温度的升高经历了从有序到无序的转变一样,这些小磁体也经历了从有序到无序的转变。局域的磁化强度相互作用就像临界点处水的密度波动一样。其结果是,这两种看似不同类型的系统在数学上存在相互的映射。
将水到水蒸气的转变映射到磁性的转变阐释了一种行为类型,是可以描述多个系统的。随着重整化群的应用越来越广泛,人们发现了许多具有相同行为的系统,尽管它们在细节上会很不一样。这个概念被称为普适性(universality)。许多系统具有相同的行为,但这些行为也有不同种类。这意味着系统可以按行为分类,这就导致了“普适性类”(universality class)这个术语的提出。幂律现象常常出现在跨尺度的行为场景,而幂律指数的值就可以作为普适性类的区分标志[4,5,9,10]。
在某种意义上,许多系统可以用相同的大尺度行为来描述的思想已经在传统理论中得到了应用。科学家对许多不同的生物系统和社会系统中都使用了正态分布。实际上,任何由充分独立成分构成的系统都满足中心极限定理(central limit theorem)要求,将水到水蒸气的转变映射到磁性的转变阐释了一种行为类型,是可以描述多个系统的。而当存在依存关系时,正态分布不再适用,其他类型的依存关系特征会导致其他系统行为。为了研究这些行为,我们必须确定各种依存关系是如何引致各种大尺度行为的。
对系统的一般数学描述有一些比较基本的方法,如用点粒子的运动来描述许多不同物体的运动,用波动方程来描述音乐片段、水波和光。虽然具体系统非常不同,但是引致其行为的依存关系,以及行为本身,在数学上是相关的(are related mathematically)。
我们可以更一般地考虑复杂系统的普适性。为了从重整化群概括出普适性概念,我们不考虑无限系统规模的宏观极限和幂律指数。相反,我们采用的表示的状态必须对应于系统在观察尺度上的状态。此外,我们不会像相变物理中做的那样用这些状态来描述的自由能,而是用它们来描述动态变化,以及系统对外力的响应。任何方程都是基于这样的假设,即使用的变量是对系统的一个有效(充分)的表示。相关参数在特定观测尺度上是重要的,由对观测者的可分辨性决定。一个系统在特定尺度上的数学表示(描述)也可能对应于其他系统的行为,即使这些系统可能有相当不同的底层组元。这就是是普适性的一般概念(图5)。
在哪些情况下,热力学极限不能揭示普适性?一个重要的例子是模式形成,如图灵斑图[26]所示,它是由大致呈现周期性的的斑点或条纹所组成的空间阵列。这些模式可以以多种方式出现,例如,化学物质的扩散和反应[27]。在足够大的尺度下,这些图案看起来只是灰色的。在这种情况下,系统行为发生在有限的尺度范围内,在足够大的尺度下自由度(degrees of freedom)会消失。不过,我们仍然可以将这些描述性变量从一个系统映射到另一个系统。这些模式表示在特定尺度具有某个结构的系统普适行为类。重要的是,这些宏观模式来自各种可能的微观行为,但它们对细节不敏感,因为这些模式的尺度很大,与微观细节是分离的。描述所形成模式的变化需要一些参数,但这些参数数量远远少于微观材料的细节。构成它们的物质的微观变化只有对相关参数的变化影响到一定程度时才能改变其模式,并且要想理解这种方式,需要先明白它们是如何影响相关参数的。
将图灵斑图纳入普适性概念,是对统计物理学中普适性概念的自然而重要的概括。这些模式随相关参数的变化,以及它们对环境条件的反应,可以用现象学观测来研究。在观测尺度下,有能力对交互行为进行预判。处理这些问题并不简单,它们给数学和观察研究都带来了挑战。生物学上采用图灵的思想来描述动物皮肤上的模式和形态发生还存在争议[28,29],一些人认为模式动态并没有捕捉到微观机制。但这个争辩忽略了普适性的关键之处。普适性应该是直观的,分子过程的细节不必用来刻画具有相似模式的个体动物之间或物种之间的变化,或者模式形成的动态过程,而且这些分子过程也不会影响这些模式在社会和生态交互中的作用。一旦用相关变量确定了系统行为的描述,对这些模式的任何遗传或环境作用都会影响到这些相关变量。行为可以通过相关变量及决定相关变量的起源和变化的基本机制进行研究。这与不用描述行星结构的细节而可以描述行星运动的能力是相似的。
对普适性的研究使我们能够确定出一些行为方式相同并且可以用一个通用数学模型来描述的系统类( classes of systems)。这就是通过对重整化群的分析和在复杂系统的科学研究中采用多尺度信息理论概括出来的普适性原则。简单地理解,就是用某个数学模型描述一类问题。
VI. 动态敏感性与混沌性
(DYNAMIC SENSITIVITY AND CHAOS)
当我们考虑一个系统的行为尺度时,我们还必须考虑到放大(amplification)和耗散(dissipation)。放大使得较小的尺度变化能够影响到较大的尺度;耗散是随着时间的推移较大的尺度行为被局限到小尺度上。在这种情况下,研究系统的时间长度被用来确定为描述系统在另一时刻的大规模行为而在某一个时刻所需要的细节层次。放大率或耗散率可能与附加信息的范围有关,这些附加信息可以作为观测时间尺度的函数用于描述某一特定尺度下的系统。
众所周知的蝴蝶效应(butterfly effect)是确定性混沌(文献[1]中的1.1节)的一个例子,这个气象系统中小的初始差异会随着时间指数性增长,这样的系统尺度和时间是混合的。因为我们对于系统的观测精度总是有限的,从可预报性的角度来看,需要讨论系统运行轨迹的分散。关于初始条件的有限信息意味着,即使系统是确定性的,系统的后期状态也无法由初始时刻的观测值决定。混沌系统具有不同程度的可预测性。行星轨道是混沌的,尽管可预测性很高。对于系统的可预测性来讲,重要的是发散率,这一般用Luyaponov指数来衡量,或者是在最大尺度上发生发散的时间尺度。对于行星轨道来说,这个时间尺度是数百万年。
从多尺度信息理论的视角来看,放大、耗散和混沌是实际系统的数学模型所必须的几个方面。虽然有些人认为建模的目的是为了预测,但是数学模型的目的应该被理解为模型要对系统具有保真度(fidelity)。混沌系统的数学模型可以像其他模型一样建立出来,但在可预测性上遇到的困难不是数学表示的问题,其预测的局限性是系统行为固有的。认识到系统内在的不确定性,建模的目的是获得可能的最好理解。要认识到,获得可能的最佳理解的能力不能与具有完全的可预测性相混淆。(更准确地说,确定性混沌的分析表示假定了一组描述系统的实参数。然而,如图3所示,复杂度曲线一般意味着在精细尺度上有更多的自由度,因此混沌行为的标准模型不能扩展到系统更精细尺度的描述上。在混沌理论不适用的尺度,需要采用其他模型。。)
将复杂度曲线应用于生物系统和社会系统,其挑战在于识别出重要的放大(与混沌无关)。考虑生物学中微观和宏观的联系。β-珠蛋白基因的一个突变,缬氨酸取代了第6位(或第7位,包括起始密码子)的谷氨酸,会导致异常的血红蛋白分子。个体中的一个这样的突变会导致镰状细胞特征,对疟疾具有抵抗力,而两个这样的突变会导致镰刀型红血球疾病。考虑社会中的微观和宏观联系。一个人的想法和观点有可能产生巨大的影响,例如,史蒂夫·乔布斯(Steve Jobs)在从个人电脑到iPhone的现代设备发展中所起的作用,他改变了数百万人的工作和娱乐方式。随着时间的推移,一个有机生物或一个社会在生理上的大尺度差异似乎可以将生物和社会系统与物理系统区分开来,但这些系统(包括物理系统)对小规模事件也可能有相似的敏感性。明显地,到更精细尺度的信息扩展对大尺度行为及其发生条件的影响是有限的。理解这些有影响的条件和细节对科学的理解是必不可少的。
突变和想法的大尺度(规模)影响来自于随着时间推移通过信息复制放大的可能性,这使得它们能实现到大尺度上。生物突变可能产生巨大的影响,因为DNA在从细胞到整个身体(甚至跨种群)复制,随后将其信息转录为许多特定功能的蛋白质。社会系统对特定的思想具有敏感性,会通过内部的机制和组织过程将这些想法广泛传播。这种过程在许多方面类似于气象系统中的蝴蝶效应。放大的条件要求在受热的海洋中有一个可用的能量源,以及驱动产生飓风那样的大尺度(规模)运动的能力。
这些过程并不违背信息重要性的框架。然而,它们确实使其应用更具挑战性,因为我们需要理解的是信息随着时间的推移而复制的方式。对微观信息的敏感性并不意味着所有的微观信息都能够或者将会以大尺度系统行为告终。并不是所有的分子改变或基因突变都会有大尺度的影响。能够改变整个社会的思想和个人,与社会上现有的众多思想和个人相比,是少之又少的。随着时间演化大尺度行为是否以及多大程度上对小尺度事件的冲击具有敏感性(随着复制,其影响会越来越大),这是复杂系统行为中信息尺度分析的一部分。在任何情况下,确认识别大尺度信息对于我们的系统分析和最终理解都是至关重要的。在原子尺度的精细细节上建立(到数学的)映射最终是无效的,关注系统的大尺度行为是必由之路。此外,正是了解哪些微观信息会对系统的大尺度行为产生实际影响,才能提供对系统行为的真正洞察。
VII. 复杂系统的一些例子
(COMPLEX SYSTEMS: EXAMPLES)
多尺度信息方法的目的是正确地表示系统的最大尺度行为,而忽略掉对于回答特定问题并不重要的微观细节。忠实于细节的表示往往是不能解决实际问题的。表示最大尺度的行为意味着确定一组可能的状态及其动力学,以及外力对它们的影响。复杂度曲线提供了所需状态数量的度量,但不管有没有它的帮助,有一些特殊方法都能确定出正确的模型。由于普适性,以前在物理系统描述中发现的宏观行为类也可能适用于生物和社会系统。普适性类分析(universality class analysis)可以使特定的系统或问题域的刻画更加方便快捷。本节中的例子主要利用了前期获得的普适性类及洞察力。将这些方法推广到更完整的一系列社会挑战和健康干预问题将需要更多的努力。这里提供的例子只是这个努力过程中的第一步。
在复杂生物系统和社会系统的研究中,一种多尺度研究方法被广泛采用,就是确定实证数据中的幂律标度行为。这已经在诸如经济时间序列、DNA 序列相关性、心跳间隔时间、网络连接性、生理和城市属性等广泛的前沿领域得到了应用[19-25]。因为幂律是标度不变的,这种多尺度行为可以被确定并被建模,而不需要太多参考重整化方法的框架。
在相变研究中,要洞察到空间同质性(即平滑性和用来数学近似的平均)被破坏,才能预计是否可以使用统计平均值来描述系统的行为。相变研究中认识到空间均匀性(即平滑性和平均作为数学近似)的破坏是一种洞察力,用来判断是否可以使用统计平均来描述系统行为。我们可以认为平均不是一种失败的方法,而是一种近似,它可能有效也可能无效,即使不是严格有效的时候可能也是有用的。这种方法常被称为“平均场”近似。原因在于,一个系统的局部行为是对作用于它的力的响应,这种力被称为局部“场”。如果我们有一个模型,它使用的是整个物质的局部“场”的平均值,而不是所有地方的实际“场”,那么不光是“场”一样,模型的局部行为也是一样的。这就成为系统大尺度行为的一个近似。事实上,这个近似方法是否失效可以用来判断哪些系统可以用传的统计方法可以描述,哪些系统需要用复杂系统的方法。复杂系统的依存关系会导致多尺度行为(multiscale behavior)。因此,我们可以预期,在生物学和社会系统中,许多情况下平均场近似会失效,这些例子会为我们提供新的见解。
我们给出的第一个例子是生物进化理论的数学分析,其中涉及生物多样性、利他主义、物种形成和寿命。随后还有一些在社会系统应用的具体例子,如种族暴力、全球食品价格、恐慌和组织的有效性等。
A. 进化动力学 Evolutionary dynamics
统计学是结合费舍尔(Fisher)的新达尔文进化论观点发展起来的[30]。在20世纪20年代,统计学是描述亲代基因组如何结合成为子代基因组的一个强有力的新方法(孟德尔定律)。在他使用的方法中,每一个子代都被视为所有可能的父母组合的一个实例。他发展出的数学至今仍然在分析遗传和性状进化,即种群生物学中起着核心作用。但他使用的统计方法只是近似,其重要性仍然没有得到广泛的理解。
这种种群生物学中的统计分析可以直接映射到物理学相变研究中发现的数学问题上。区别在于,进化动力学的分析是用动力学方程代替原来的物质平衡描述。在每个案例分析中,数学都是从系统状态的概率描述开始,这与组元状态有关。
正如一个材料的不同局部可以处于不同的状态——液态,气态,一个种群中的生物体可以有不同的可能基因组,即等位基因组。整个种群是众多有机体构成,单个有机体都是基因的组合,每个基因都有自己的状态(几个等位基因中的一个)。费舍尔做的假设是,一个基因位被分配一个等位基因的概率会独立于该生物体的其他等位基因的具体状态和其他基因组的具体状态。但微妙之处在于,这个概率并不独立于该生物体内其他基因的基因组的状态,甚至不独立于其他生物体基因组的状态。(等位基因在种群中存在的概率和随机样本中遭遇的几率本质上是一样的)。一个基因的状态独立于其他基因或基因组的状态。数学上,所有生物体基因组的概率可以写成单个生物体状态的概率的乘积,甚至也可以写成单个基因状态的概率的乘积。这是一种通常的分离尺度平均场近似方法,即P ({si}) = ∏i p (si) ,其中P ({si}) 是整个系统(材料,或所有生物的基因组)的状态的概率,p (si) 是特定状态下单个组元(材料的一小块区域,或单个基因)的概率。这儿的依存关系大体如此:一个组元的特定状态不影响另一个组元的状态,一些组元的状态概率才会影响其他组元的状态概率。这个区别看起来很小,但在数学上却是至关重要的。
为了让讨论更容易,我们将使用道金斯(Dawkin)在他的书《The Selfish Gene》(中文译作《自私的基因》)[32]中使用的“划船者的类比”来解释统计学的方法和它的失败。
我们考虑划船者(桨手)队伍之间的比赛。每个桨手类似于一个基因,而整个船类似于有机体。存在一个桨手储备库,桨手被从库里挑选出来安排到船上,所有的船都有相同数量的桨手。船之间相互竞争,优胜者被放回桨手池获得可能再参加比赛的机会。为了弥补那些输掉比赛的桨手,使储备库总体数量始终保持一致,成功的桨手将被复制而数量增加。
道金斯描述的一个例子是说英语和说德语的桨手之间的竞争。语言会对比赛产生影响,一艘船上说同一种语言会更具优势去赢得比赛,因为桨手能相互理解。随着时间的推移,储备库会发生什么变化?如果开始说英语的桨手比较多,一艘船上的桨手都说英语的可能性更大。而一个德语桨手的同伴也更有可能是英语桨手。这意味着说英语的桨手比说德语的桨手更容易赢得比赛。随着时间的推移,说英语的桨手数量将会增加,说德语的桨手的数量将会减少。最终将会变成一个全部说英语的桨手储备库。或者,如果我们从一个说德语更多的库开始,随着时间的推移,说德语的数量将会增加,最终我们将得到一个完全说德语的库。在上面任何一种情况下,我们都可以把这看作是桨手之间的竞争,随着时间的推移,一种类型的浆手会赢过另一种类型的桨手。
道金斯的论点似乎是合理的,但是这儿有一个隐藏的假设会产生意想不到的影响。这个假设隐藏在桨手们是如何被挑选出来放到船上的。作者假设这是随机的挑选。但如果我们不这么做会怎么样?例如,让储备库中所有的桨手总是排成一队,前面的人先上船参加比赛,而赢了回来的人及其复制品都排到队列后面。在这个新假设下,动力学过程将变得非常不同。
新情况下,在队列的某个地方,往往会聚集同一类型(说英语或德语)的人。队列中不同地方所聚集的类型可能会不一样。这种区块状结构会导致整体的多尺度结构区块状的存在使得这一过程不同于前述的混合式情况。此外,在描述系统时,仅仅识别出存在区块状格局的是不够的,还要了解由于边界移动导致的区块变化。系统的动力学描述要包括这些区块的多尺度动态过程。
这个排成队列的过程会和前面的随机挑选情况不同,在新情况下英语和德语会长期共存。虽然这个或那个语言可能终将消失,但相对于原来说的随机混合模式,新模式会需要运行更多的世代(时间)才能发生灭绝。有趣的是,这可能也是真实世界上说英语和德语的人能共存的原因。如果世界上的人都经常混杂在一起,那么很可能将来只剩下一种语言。但是如果说德语的人生活在世界的一个地方,而说英语的人生活在世界的另一个地方,那么就可能有多种语言共存——有些地方说英语,有些地方说德语。现在,当人们比过去移动更多时,人们更倾向于说一种语言,这是有道理的。
随机挑选桨手与非随机挑选之间的差异可以从划桨者在船上的概率分布来理解。随机抽取意味着一个特定桨手的可能性是由桨手储备库中的划船者类型的概率给出,与这个船的其他桨手或者其他船的桨手类型无关。这就是平均场近似。当我们把他们从一个队列的某一部分挑出来时,这个桨手的类型的概率就不再与前后选择的桨手类型相独立,相对从整个库随机选取的方式,他们属于同一类的概率会更大。
桨手队列的生物学类比是在地理位置上彼此相邻的生物体进行交配(或者根据性状进行交配,某些生物体更倾向与类型相近的其他个体交配,即选型交配)。对于动物或植物来说,进行繁殖的地方靠近它们出生的地方就足以显著地改变新达尔文理论的结论。对于那些还不熟悉平均场和非平均场行为差异的人来说,这种变化是令人吃惊的。
认识到生物种群不能用平均场近似来描述的第一个结果是,种群可以比传统种群生物学所预测的更加多样化[43,44]。解释生物多样性是费舍尔工作的核心动机,因为先前的理论不能解释在自然界中发现的高水平的生物多样性[31]。他的改进结果超越了传统的统计学,而突破他所介绍的近似方法会有更大的多样性。在混合良好的种群中,多样性会呈指数性下降。如果混合得不好,多样性会持续更长时间。有趣的是,许多种群生物学的测试实验都是在种群混合的实验室里进行的,这种实验条件和“混合”的理论假设是相符的。但如大家所知,实验室里的物种的基因型非常一致,而自然群体中的基因类型(野生型)更具有多样性,这与它们不是良好混合的预期结果相一致[33-36]。
第二个结果与特定形式的多样性——物种分化有关,即随着时间的推移一个物种分为两个或多个物种。这一过程如何发生一直备受争议。如果我们考虑物种初始时在每一代交配时是混合的,那么他们怎么停止混合了?但如果我们采用非平均场描述一个物种,那么物种分化会由个体更愿意与同类型的物种繁殖而产生[37]。这个想法的空间种群模型已被证明能很好地描述自然的生物多样性[38],在一个高维的图灵斑图上,不同类型的区块自发形成空间格局,形成多物种共存的状态。
第三个结果与进化中的利他、利己,以及竞争对于合作的优势有关。从费舍尔的统计方法得出的一个关键结果正是道金斯所科普的观点——“自私的基因”。根据这种观点,个体基因所具有的性状只会有利于其自身繁殖成功的可能性,而与整个基因组、族群或物种无关。费舍尔的统计假设证明了基因的自利性。一个重要的问题是,当这些假设不成立时,这个结论是否还有效。答案是无效的[45-47]。种群的自生成区块创造了新的动力学过程,这不能用基因的自私性来解释。因此,突破平均场近似对于理解为什么基因之间的竞争不足以描述进化过程是很重要的。这个问题已表现为关于利他主义的激烈争论。如果“自私的基因”观点成立,那么在不同生物体之间的利他行为产生的唯一可能就是它们具有相同的等位基因(一个有机体帮助另一个有机体以让自己的等位基因在下一代中得到增加),而且利他的程度会受到等位基因共享程度的限制。从数学上看,这种思想也体现在一种叫做“亲族选择”的机制中。直到现在,关于“亲族选择”是否足以描述进化或是否需要考虑群体中的关联作用还存有争议,后者被称为“群体选择”理论[39-42]。当前,这个争议往往只在平均场近似下讨论,由于此时两个理论在数学上是等价的,使得这种争议沦为一个概念问题而不是数学问题。当我们超越平均场近似时,我们会发现只用“亲族选择”用来解释进化是不够的。
我们可以从桨手储备库的思想看这是如何工作的。考虑这是一个利他和利己桨手的结合。如果桨手排成一个队列,会有一些利他的个体和利己的个体形成的区块,利己个体的表现要比利他的差。这是因为利他者一般靠近其他利他者,利己者则靠近利己者。利己者无法利用利他者,因为在储备库中的位置并不靠近,从而不能上同一条船。但在随机选择的情况下就不一样。尽管如此,在队列中还是存在一些利己者和利他者靠近的边界区域,我们需要了解边界区域会发生什么。因此,进化动力学在很大程度上受到边界性质的控制,即边界是“相关的”。而新达尔文主义的方法完全不是这样,它只关注等位基因的性质。依赖于区块和边界如何工作的结论不能被亲族选择所描述,它们对利他行为有不同理解。
第五个结果与现实中全球范围内使用飞机和其他交通工具的出行比率不断上升[48]有关。我们已经看到,混合导致的平均场行为类型与上面的空间模型非常不同。日益增长的输运使我们更接近混合情况,这会使得生物多样性减少。我们确实看到,物种入侵正逐步消除物种的地方性差异。另外,广泛的远程输运也会引发传染病的病原体发生改变。当一种病原体只能在局部传播时,最具侵略性的毒株会灭绝,因为它们会在其局部地区杀死所有当地宿主。但随着输运量的增加,区块变得无关紧要,那些更具侵略性和致命性的病原体会成功,造成致命性流行病的日益蔓延。理论分析表明,地球上曾出现过区域性的物种灭绝,而远距离输运量的增长会导致危险程度增大,这可能造成全球性物种灭绝。这个分析还可以对埃博拉病毒和其他严重疾病的防治提供重要的应对建议。
第六个结果是关于寿命进化的研究,涉及如何延长寿命的建议[49]。在寿命研究中,平均场近似表明进化不能选择特定的寿命长度,因为寿命延长总是有利于繁殖。然然而,地域性的增殖繁衍会将其有机体和他们的后代关联起来,个体的寿命由影响好几代的生态条件决定,比如当地的可利用资源等。寿命是由生态条件选择决定的,对生态运行机制的干预才可能获得寿命的延长。
因此,我们看到,新达尔文进化论观点还存在许多问题。它是思考进化问题的一种有用且有力的近似方式,但它并不总是正确的。在理解生物多样性、物种分化、利他主义、疾病、寿命和其他重要的生物学领域,新达尔文理论还没有完全描述清楚。
B. 多尺度生物多样性(Multiscale biodiversity)
本小节将复杂度曲线直接应用于生物多样性分析,对复杂度和尺度的评估会直接关系到对(多样性丧失时)物种脆弱性的理解。
因为直接开发、自然生境的减少以及入侵物种的全球性输运等影响,生物多样性的丧失正对全球保护工作提出挑战。物种多样性在全球的异质分布对全球物种保护有重要影响,这体现在针对多样性热点的保护措施中[50-52]。单个物种内部基因多样性的保护[53,54]是这个物种面对环境变化和疾病而生存的重要因素[55,56]。生物多样性的多尺度特征表明,物种内部的多样性也是分布不均的。遗传性特质具有无标度的幂律分布特征,这意味着多样性不是等比例的,大部分多样性集中在小的亚种群中。多样性有其自身内在的动力学,这与可能的外部影响(例如生境变化和物种相互作用)不同。多样性的增长只能是逐渐发生的,但是由于一些稀有类型的死亡,可能在没有外部干扰的情况下会发生大幅度的下降。
要分析生物多样性,不仅要考虑物种中存在的基因组的多样性,还应考虑特定类型的重数(重复的数量)。这是复杂度曲线的反函数,也就是说,如果复杂度曲线是多样性作为尺度(规模)的函数,那么基因组的多样性就是规模(冗余)作为多样性的函数。多重性是种群结构的指标,可以使用物种成员的数量来定义,即,衡量物种中某个范围基因类型的规模(尺度)。评估生物多样性,可以通过测算物种间的多重性分布[57],或物种内亚型的多重性分布进行。
有一个利用多重性来评估生物多样性对灾害稳健性(robustness)的重要意义的一个例子。有人提出,即使灭绝95%的物种,也会保留80%的生命树(总的多样性),所以保护多样性的生态规划是没有建设性意义的[58]。之所以获得这样的结论,是因为其假设了随机损失,这样,当整体损失很大时,也不会消除生命树的某一个深度分支上的所有个体,即使它们的数量只占总体数量的很小部分,从而能保留大部分多样性。多重性分析恰恰表明保护规划很重要,可以大大改善多样性的保护。随着时间的流逝,多重性小的物种的一些直接损失会因为这个种群的生态脆弱性(小的残余数量容易灭绝)而最后招致大的损失。从种群的多重性可以看出相关生物体的残存小种群的脆弱性,因此也可看出,尺度和多样性都很重要!一大部分近亲物种(或近亲生物)的消失会使该群体的幸存部分极易灭绝。虽然一个群体中至少有一种生物可能存活,但该类型的生存能力受到损害,很可能随后就灭绝了。这个结果是因为小尺度(规模)多样性的不稳健与大尺度(规模)多样性的稳健性造成的。它表明,在物种灭绝期间或灭绝后,通过保护规划[54,55,59,60]来确保稀有物种的繁殖,可以显著提高物种多样性的保持率。
使用普适性和重整化群/多尺度信息方法似乎很难研究复杂的社会经济系统。但是,有几个例子显示这种应用具有可能性。第一个例子有助于阐明种族暴力的根源及其预防[61,62]。
种族暴力通常是根据暴力冲突参与者的环境条件来描述的,包括历史、经济、政治、领导和其他社会方面。种族暴力通常是群体行为,涉及多个决定者和参与者,而不是类似国家政治领导那样的单个决策者所促使的。这个情况标志着相关大尺度(群体)参数进行分析才是有用的。在这种情况下,我们如何应用普适性的论点,以确定与种族暴力是否发生有关的少量社会系统指标(few measures of a social system),从而帮助确定发生暴力的地点或时间以及该如何预防暴力。
这是通过建立一个理论框架完成的,该框架仅考虑不同类型的存在,而没有明确处理其他因素。这样的框架将分析简化到只限于问题的核心描述,即,若不区分类型,就不会有种族冲突,不需要先验的其他条件。其他因素可能会起作用,但是我们假定它们只与类型的动态变化相关。如上文在相变处理中所讨论的,空间维度会是相关的,因为人类种群的行为大约是在二维空间,我们的讨论将包括这些维度。
具有这些属性的最一般的模型是一些不同的具有空间分布特征的类型,它们的变化遵循一个包含空间移动的动力学过程。模型有两种不同类型的行为:混合和分离。这和合金材料中局部运动一样,它们也可以混合或分离。之所以发生分离,是因为能量(原子)或社会(人类)偏好,个体倾向于处于同一类型的成员附近;而分离表现为随着时间的推移形成越来越大的群体。普适性意味着微观参数不会影响系统行为,除非是一个控制逐渐增大的团体形成速率的乘性常数(multiplicative constant)。这个系统的唯一描述性参数是区块的大小(patch size)。迁移会导致个体大规模移动的系统,这些移动又促进了区块的产生,在我们看来,区块的大小是外加的(extrinsically imposed)。
既然只有区块的大小作为相关参数,就必须考虑该大小如何影响种族暴力。而(讨论合金的)物理定律没有给出这种关系的标准解答,但从直觉上讲,在两个极端中的任何一个中都不会出现暴力行为。首先,当邻里充分混合时,个体不能选择分离,个体都是单个地看到其他类型的个体,我们假设这种极端情况下不会有大范围的暴力行为。另一个极端是区块很大时,整体上个体看不到其他类型的个体,也不会发生自发的暴力。这样,暴力只会发生在区块具有特定的中间尺寸情况。在确定了导致暴力的单个相关参数是区块的大小之后,剩下的工作就是通过对实际暴力现象的观察来验证分析。
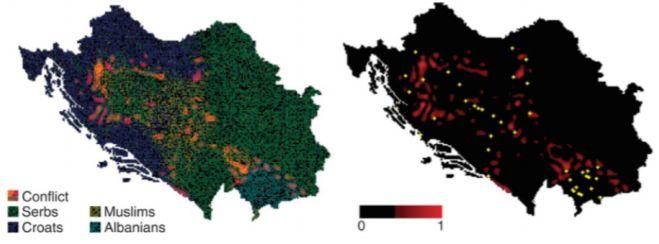
图6:1991年南斯拉夫人口普查数据被转换成空间表示形式[左],并用多个体模拟预测可能与邻近群体发生冲突的人口[红色叠加层,左和右]。该预测与报告为大规模战斗和屠杀地点的城市位置[黄色圆点,右]非常吻合(相关性为90%)
与前南斯拉夫和印度的种族暴力实证数据进行比较(图6),证实大小为20-60公里的区块与种族暴力的位置具有高度的空间相关性(达到90%)。可以从社会学角度解释这一结果:分离限制了族群间的摩擦,而混合抑制了族群间的异化。在一些地方,分离出的自我认同群体地理区域达到临界尺寸(规模),群体会开始在公共场所内施加其文化规范、宗教价值观、语言习惯和某些群体内社会信号。这些场合可能包括公共广场、市场、餐馆、宗教场所和学校。而当其他群体的成员违反了社会期望时,由此产生的摩擦很可能导致某些族群的激进行为。对于大于临界地理尺寸的区块,个体主要是在自己的区域(同一族群)内,存在事实上的地方主权。如果区块小于临界面积大小,那么种族群体就无法对公共场所的行为强加自己的规范和期望,从而使当前的多个种族群体和平共处。该讨论进一步表明,自然边界和政治边界的存在可以增加自治权,以实现隔离,可以防止可能发生暴力的地区发生暴力。对瑞士的分析表明这个模型既与导致其基于联邦治理结构的行政区格局形成的历史事件相一致,也与当前关于语言和宗教团体的人口普查地理数据相吻合,对历史上的暴力和当代的和平都能给予解释[62]。
这个理论与南斯拉夫、印度和瑞士的实际情况的一致性很好地验证了我们用来确定高度复杂的社会系统中相关参数的方法,这促成了确定种族暴力及其预防的位置和机制的理论。该研究进一步证明,精心设计的州内政治边界和自然形成的良好地形边界(如瑞士)都可以减少暴力倾向,这提供了必要时可以使用的一种比完全融合或分离来促进和平共处的更可取的有限干预方法,可以考虑应用在世界上许多容易发生暴力的地区。
在模型的背景下可以考虑其他社会和经济力量。第一,将地理区块的大小确定为相关参数,不仅允许暴力与区块的大小相关联,还有许多其他社会属性也可能有关,如一些经济和社会条件也可能与区块的大小有关。如果将区块的大小用作自变量,则这些属性与暴力以及彼此之间的相关性可以揭示这些依赖关系。
第二,类似于迁移和政治壁垒,其他外部力量也会影响系统的行为。这些大尺度的力可能会制止或促进暴力。一个相关的例子是独裁者的作用,例如前南斯拉夫的铁托(Tito),其铁腕统治压制了后来频繁发生的暴力行为。另一个外部力量的例子是像瑞士一样的集体决定以施加政治边界,或是像在新加坡决定并实行的强制混合居住的公共住房(组屋)政策。这些不只是外在力量,它们是在实际上利用了理论中发现的理解来影响系统本身。与物理学一样,对系统行为的理解能促进发现可以影响系统行为的干预措施。
我们注意到,将人口的地理区块大小确定为与种族暴力相关的参数是一个科学假设,实证数据的验证是对该假设有效性的确认。但是,通过多尺度信息(重整化群)方法可以得到同样的假设,这也证实了该方法可以为广泛的复杂系统生成“假设”。这种方法之所以很重要,是因为确定出用于复杂系统检验的正确(低维)假设本身就是一项困难任务,很容易不成功——系统存在大量的潜在假设,由于虚假相关等问题,在对每个假设进行检验时,统计检验的有效性会受到影响。在这种情况下,就像在多尺度分析的其他应用一样,确定出重要的假设可以为复杂系统的理解提供强大的理论基础。
D. 市场价格动力学(Dynamics of market prices)
作为多尺度信息方法的第一个经济示例,我们回顾了最近对商品市场中的泡沫和崩盘进行的分析[64,65],这些分析结果与实际价格行为精确相符。
图7:价格变动本身会刺激交易者,从而导致交易者之间的相互影响,购买可以引起更多的买入,卖出可以引起更多的卖出,最终这种从众效应会引发市场价格泡沫或暴跌。更准确地说,泡沫的产生是两种不同类型投资者之间地相互作用:一种是跟随趋势的投机者,他们在价格上涨时买进,在价格下跌时卖出;另一种是基本值投资者,他们根据供求信息,低价买进,高价卖出。
传统的市场理论假设人们都是独立而理性地进行投资决策,因此可以预测供求平衡。有趣的是,在对市场泡沫进行复杂系统分析时,不是理性假设有问题,而是独立性。由于商品市场的趋势跟随,个人的行为并不完全独立。相反,个体的决策会影响他人的决策,也会受到他人决策的影响。这些影响导致个体的行为组合为集体振荡(图7)。该示例展示了一个描述系统动态行为的大尺度时间序列模型。在物理学中,学者用重整化群的动态随机方程组来描述材料生长[17]。我们的应用比这个物理问题更简单,只有一个动态变量,并且在这种特定情况下,随机项也不是必需的,但是这二者的框架是相同的。
为了构建食品价格变化的动力学模型,我们将价格的变化写为:
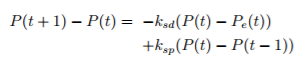 (1)
(1)
这只是扩展到系统变量描述的一阶情况;这些是影响行为的最大项。多尺度信息方法论证明仅使用最大的项是合理的,因为全球粮食价格仅受许多单个组元在最大尺度上的集体行为的影响。第一项可以看做是低买高卖的投资者行为,其基准价格由供求关系确定。第二项可以看做是趋势跟随的投机者行为,他们在价格上涨时买入,在价格下跌时卖出。第一项给出了传统均衡市场的动态版本,并扩展到包括导致内在的自我产生的动态价格行为。在更完整的模型中,添加了趋势追随者转换市场的倾向。当价格发生急剧变化时,投机者随着价格上涨而入市,而随着价格下跌而离市。
如果没有趋势追随投机者,那么低买高卖投资者的行动将导致价格指数衰减到均衡状态。有趋势追随之后,系统会具有不同的行为,这取决于它们的存在强度,即系数Ksp的大小。如果商品的价格上涨,趋势追随者会在价格上涨时买入从而将价格进一步推离均衡。但是,价格离均衡越远,参与其中的“低买高卖”的传统投资者就会越多,他们的卖出行为提供了推动价格回到均衡状态的力量。实际上,价格偏离均衡的距离越远,这种向均衡的驱动力就越强(经济学中称之为“瓦尔拉斯力”),最终会逆转价格的上升趋势。此刻,从众效应的跟随趋势会驱动价格下跌,最终超过平衡,最终重新开始新的周期。这些相互作用会导致价格偏离均衡的振荡。相比计算不稳定的均衡价格,更好的方法是将相互依存关系包括进来确定系统的大尺度模式,并将其准确地映射到(全球粮食价格所表现的)泡沫和崩盘上[64,65]。
长期以来,泡沫和崩盘一直是经济学理论上的一个热点主题 [66, 67],但其动力学的直接数学表述尚未成型。自1990年以来,由于趋势追随而导致的均衡破坏已得到充分证实[66,67]。但是,当时的理论并不能展示系统的泡沫和崩盘过程的动态。为什么传统的方法论没有考虑非独立性的动态影响?如前所述,一个关键的限制是经济学中的传统数学方法仅适用于微观和宏观之间具有行为分离特征的系统(尺度分离),而可能导致(如趋势跟随引发的市场泡沫这样的)大尺度行为的各部分之间的相互作用违反了这种分离。取而代之的是,许多论文都提到了投机者的可能作用,但并未在数学上对其影响进行建模。最近,关于多主体建模的研究表明,市场动态可能会偏离均衡价格[69-72],但这些方法还未用于食品价格建模,而市场代理人的建模通常会有大量参数去描述许多可能的代理人行为。通过在等式(1)中价格行为的动态表达中包括最大作用项,并引入描述市场转换行为的项,就可以得到对价格的准确描述。
认识到这种方法与基于相关性的时间序列分析之间的区别也很重要。在相关性分析中,多个时间序列与特定的目标时间序列相关,并且该相关性被用作时间序列对目标时间序列的影响(或关联)的度量。但此类相关性分析不能刻画影响的尺度,因为相关性与尺度无关。这可以用统计学中的相关性来解释,也就是说,在统计上可以肯定的是,在给定大量不同的时间序列,即使它们是不相关的,但是它们中的一些序列也会表现出相关性,这就会导致其他许多互不相关的序列表现出潜在的错误关联。采用这个方法需要非常谨慎来确保不会发生这样的错误,但诸多批评表明这种错误在很多实证工作中是常见的[73-76]。相反,采用尺度分析可以排除许多潜在的关系,尤其分析系统最大尺度的情况时。
E. 网络动力学及集群行为:恐慌和市场价(Network dynamics and collective behaviors: Panic and market prices)
另一个市场价格应用的例子涉及对股票市场中恐慌行为的研究。该分析从一个系统动力学的通用模型开始,这个系统具有一个内部作用和外部力量的网络[78]。其应用于市场的验证性工作已经发表[77]。
从复杂系统的角度,可以使用以下方法来评估市场行为,包括网络拓扑模型、基于代理人的模型,以及我们正在讨论的聚焦于大尺度行为的方法。本文提供了大量参考资料来说明和对比不同的方法。我们在这首先介绍基本问题和动机。
恐慌是社会系统中的重要集体行为之一,是社会学和经济学中研究的相关问题。在社会学[100-103]中,恐慌被定义为离开实际威胁或想象威胁的集体逃避。在经济学中,银行挤兑的发生至少部分是由于银行挤兑本身给个人带来的风险,挤兑可能是由于诱发条件、外部(可能是灾难性的)事件,甚至是某种随机引发的[104,105]。尽管通常认为市场行为反映了外部经济信息,但经验证据表明,外部事件并非唯一的市场恐慌原因[106]。尽管对恐慌的实证研究很难进行[107-109],但将内源性(自产生的)和外源性市场恐慌与市场指数的波动区分开来的努力已经取得了一些成功[110-114],尽管其结论还存在争议[115-118]。
2007年至2008年的金融危机引起了人们对分析市场崩盘行为的兴趣。一个重要的问题是,2008年的崩盘到底是由令人关注的经济新闻造成的,还是由与负面新闻有关/无关的的恐慌导致的?通常,迅速下跌然后不久恢复的市场行为使人们怀疑“市场能反映有效经济新闻”的经济学假设。然而,在“基本价值决定价格”的均衡概念之外,经济理论并没有为市场行为的描述提供坚实的基础。这并不奇怪,因为经济均衡的想法与重整化群之前的热力学和统计力学中存在的统计概念和数学优化方法相同。另一方面,恐慌和其他集体性社会行为应理解为自我产生的行为模式,其中众多个体之间的相互作用引起大尺度的动态变化而无需外部力量。这种有序的行为以及可能由于恐慌发生的无序和有序之间的转变恰好符合这样的条件,此时,基于空间平均(个体之间的同质性)和时间平均(稳态)的统计假设和优化不再适用。
从基于网络拓扑的方法角度来看,主要的方法是将系统作为一个稀疏网络刻画,具有异构性节点[79]和动态性连接[80,81]。为了确定风险的标志,金融网络主要是根据股票价格的相关性定义的[82-85],当价格的相关系数高于阈值时,这些股票就会被连接起来,该阈值被设置得足够高,以使连接具有稀疏性 [82, 86-92]。例如,Bonnanno等人[87]的研究表明,相关性的生成树表示[82]在“崩盘”期间呈拓扑收缩并且具有不同的幂律指数。Harmon等[91]分析了网络,揭示了危机如何在经济部门之间传播,表明部门间的防火墙可以减少大尺度风险。
基于市场参与者交易策略的代理模型也被用来描述市场行为。模拟通常会考虑两组市场参与者:“基本值交易者”和“噪声交易者”[70–72]。基本值交易者考虑资产的价值,而噪声交易者还考虑价格的动态,这可能导致羊群效应。模拟表明[71]随着交易者从一组转移到另一组会涌现出实证所观察到的波动性聚类和幂律标度行为 [89, 93, 94]。
我们在本文中描述是第三种方法,就是复杂系统的多尺度表征,其重点在于对市场价格 [95–97] 的集体动态进行建模,并通过最少的相关参数集来表示。
为研究市场崩溃而发展的多尺度模型着眼于市场价格行为的两个特征。第一个来自传统的经济理论,它认为市场价格反映了对基本价值的感知,因此市场价格的变化是由新闻(即改变基本价值的感知的新信息)驱动的。第二个是内部的自强化行为(internal self-reinforcing behaviors),这也可能引起价格动态。结合这两者,可以构造出具有外部影响和相互影响的大尺度系统行为的通用表示。分析所得的网络响应模型可以获得任意规模大小全连接网络中同时同向移动的元素比例(联动指数)的精确统计分布 [95, 96]。通过归一化考虑拓扑对环境耦合的影响后,分析结果对于其他网络拓扑,包括随机网络、规则晶格网络、无标度网络和小世界网络,也是非常好的近似。与普适性概念一致,此模型及其分析结果可以描述各种各样的网络系统,从Ising模型的Glauber动力学 [95, 96] 和种群遗传学的进化动力学 [121, 122] 到反映社会系统中从众和非从众的社交网络上的意见动力学 [123]。在这里,我们只是描述了其对金融市场的一个应用。
穿越模型的参数空间,系统行为表现出有序到无序的相变,类似于图2中水到气的相图。该模型有两个参数,它们一起控制内部和外部原因的相对重要性,以及正向和反向外部影响的相对比例。当我们在参数空间中移动时,在“共同运动”部分的统计分布中可以观察到三种不同类型的行为。在内部相互作用较弱的无序区(对应于水的相图中的高温情况),我们有一个“上升”相,对应于一个有偏的分布,其中大部分股票上涨(正价格变动),以及“下降”相——对应于另外一种有偏分布,只有少量股票上涨(负价格变动)。当上下平衡时,分布会在50%分位数左右上有一个单峰。随着元素之间交互作用强度的增加,存在着向集体有序的过渡。在有序区,存在双峰分布,因为内部相互作用而导致两个不同的相存在,相互作用使得大部分元素要么向上运动要么向下运动,它们之间的动态切换很慢。这种切换(翻转)对应着一阶相变边界。该模型的二阶临界点,即无序状态和有序状态之间的转换,是唯一具有平坦分布的状态。
该模型与多只股票的动态有关,而不只是单个股票的行为。这个行为也可以由交易代理人模型产生,通过它们之间的影响网络来表示。但是,许多细节是不相关的,而需要被抽象为聚合行为。如上所述,网络的结构不会改变行为,并且与交易者代理人模型不同,价格代理人的行为规则不需要不同。我们发现,自然行为是独立行动和集体行动之间的一种过渡,后者可以被认为是恐慌。这有助于确定集体恐慌的度量方法,并将其用于预测恐慌发生后引起的金融危机。
将恐慌的概念与影响模型联系起来,恐慌中的模仿对应于相互影响。衡量市场动态的大多数标准指标是波动率和平均相关性。作为替代,通用模型建议将联动指数(co-movement)作为大规模集体行为的一种度量。联动指数与波动率或相关性之间的本质区别在于,若价格变动之间存在相同的关系,但单个价格变动变大,会让波动率和相关性都会变大。这样,即使价格走势大多是独立的,这也可能导致较大的波动率或平均相关性。不同的是,即使价格变动很小,联动指数也可能很大。因此,联动指数可能是我们一直寻找的集体行为的更直接的度量指标。这个假设是有道理的,联动指数对于描述恐慌和神经紧张会很有用。
通用模型被分析,联动指数的分布被计算出来,其预测能力被日市场行为的实证分析所证实。值得注意的是,这些预测在真实的金融数据上得到了证实,涵盖了近期的经济危机以及早期的市场动态。联动指数数据还可用于评估最近的市场危机和历史的单日崩盘是内部产生的还是外部触发的。在分析时,现实世界的行为将仅采用参数空间的平衡的正负新闻一维子空间来处理。联动指数的高水平临界点(即恐慌)被发现可以单一地识别2008年的市场崩盘。由于临界点是唯一的,因此无需调整模型参数即可获得此对应关系,因此可以将其视为金融危机的零参数理论。此外,联动指数值在市场崩盘之前一天就已经大大增加,它为即将发生的崩盘提供了一个明确的预警信号。因此,持续性增强的恐慌行为是每个市场崩盘的预警信号。
这个模型预测性能非常好,它预测了25年以来的一些最大日崩盘,没有任何误报或漏报。一些其他测算可以用来预测市场危机,如波动率、股票价格之间的相关性和协方差。这些指标中,波动率和相关性是最常用的风险预测因子,但它们的预测能力最低,有三个错误预测和四个正确预测;协方差是一个相对较好的预测因子,只有一个错误;多尺度模型提供了最佳的预测效用,没有任何错误 [97]。
我们注意到,联动分数的大小分布(股票价格向同一个方向变动的数量,即行为一致的成员数)是类似于复杂度曲线的多尺度分解。
F. 原理和多尺度分析(Principles and multiscale analysis)
在本节中,我们将回顾根植于复杂性曲线中的多尺度分析中的几个一般性特征和原理,以便在不同的复杂系统上应用。关于多尺度分析的原理及其在构架基本结构理论中的使用以及对多尺度结构的其他度量(如信息的边际效用)的更多讨论,可以参考 [124]。这些原理将提供了一种对社会和生物系统的一类应用的理解方法,该方法已被发展用于理解各种系统之间的结构和功能之间的关系。利用多尺度信息建立模型需要具体的数据来描述系统的尺度和动态行为。但是,在某些情况下,特定尺度的信息量本身可以提供对系统行为的洞察。在这里,我们关注一些这样的示例,以说明复杂度曲线的功效。
G. 求和规则:基本激发强度(Sum rule: Elementary excitation strength)
多尺度分析可以评估跨尺度的系统行为。特定尺度上的自由度的程度或数量由复杂度曲线给出,而复杂度曲线的测量方法与用熵描述微观尺度上自由度的方法相同。有研究表明,跨尺度的自由度之间存在基本的此消彼长[1, 14, 15]。这是由于大尺度行为源自于组元的一些相关性,这就是对微观自由度上的约束。行为涉及的组元数量越多,该行为的尺度(规模)就越大,相应地,较小规模上的自由度也就减小得越多。系统的这种基本特征可以用求和规则来表示,即,尺度加权的自由度总和与系统的结构无关,只决定于组成系统的组元的数量。可以看出,该求和规则类似于介电响应函数的求和规则,即,作为集体行为的激发(如等离激元)减少了单粒子基础激发对响应(权重)的贡献 [125]。
H. Ashby 定律及多尺度信息(Ashby’s law and multiscale information)
控制论的中心原则是,要使(试图控制其环境的生物或工程系统)控制系统有功效,其可能状态数量必须与环境的可能状态集相匹配。最优化设计的系统也有可能控制失效,其失效的程度与其可用状态相对于环境状态数的相对数量差异有关。这就是必要多样性的Ashby定律,它是基于这样的假设而得到证明的:必须将环境的每个状态匹配到不同的系统状态,以便应对以减轻环境带来的影响。
但是,这一说法是在一个环境差别基本上具有相同尺度,并且该尺度与系统状态的差差异相匹配的背景下提出的。若宏观控制系统的状态差异没有满足环境状态的微观差异,系统状态的改变可能永远无法成功地抵御环境所施加的巨大力量。为了纳入这些实际情况,需要对必要多样性的Ashby定律进行多尺度的泛化,到识别的环境和系统的行为尺度上。直接的泛化会涉及在环境影响的相关尺度下计算系统的状态数量 [14]。
这就直接将作为多尺度变异性量度的复杂度曲线与系统行为的有效性联系起来了。
I. 关于复杂度曲线的形式理论(Formal theorems about complexity profile)
这里是有关复杂度曲线的一些定理,用于对实际系统的思考和近似分析。形式如下:
独立组元特性——整体复杂度曲线是各个独立组元的复杂度的和,即
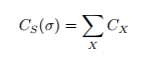 (2)
(2)
完全非独立的组元特征——n个完全非独立组元X的复杂度为
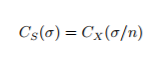 (3)
(3)
结合上述完全独立和完全非独立组元情况,我们得到可以同时描述完全独立和完全非独立情况下的复杂度曲线,
 (4)
(4)
如果要成立, n(X) 组件的不同集合X必须彼此独立。我们可以认为n(X)是组元集X的尺度。
J. 基于数据的多尺度信息计算(Calculations of multiscale information based upon data)
有一些公式可以基于系统行为的数据用于计算复杂度曲线。
第一个是从系统在系统不同状态的概率P (si) 得出的。尽管已证明该公式是唯一的,但由于对所有子系统进行组合处理,因此该公式在计算上有难度,只能针对有限规模大小的模型系统(包括Ising模型,高斯相关性和其他几个系统)进行计算 [126–128]。
学者已经研究出了一种在计算上更易于处理的方法,用于基于关于系统的抽样数据进行的复杂度曲线的近似评估 [129]。此方法不但考虑了系统中彼此连接的组元,而且在组元数量的尺度内,对连接到一定程度的组元进行了数量汇总。
系统的更简单的近似和计算,这对于实际问题的处理可能也很有用。特别是,我们可以通过考虑相互连接的组元集来得到复杂度曲线的近似。计算每个集合的组元数量时,我们可以把它们近似为彼此完全相连的。计算某个尺度或更大尺度的集合的数量,可以得到与该尺度对应的的复杂度曲线的值。这就是根据前述章节的定理得到的对于复杂度曲线的近似。当系统在独立和非独立构成之间有足够清晰的区别时,此构造会有所帮助。一些改进的近似方法还考虑了依存度,详情参考文献 [129]。
K. 组织响应(Organizational response)
对社会系统复杂度曲线的第一个近似值是,考虑多个人从事一项特定的活动,个体行为相互联系,以此作为该活动的尺度(规模)。每种活动都可以描述为这些个体的特定状态。例如,两个人在使用横锯时必须采取相应的协同动作。多个两个人的团队可能同时工作,但是他们的行为不一定要协调。系统特定尺度上的复杂度是作为社会组织的一部分而参与协调行动的群体(或独立的个体)的总和。然后,可以将该近似与必要多样性的多尺度法则相结合,以分析特定组织(即旨在执行特定功能而组织的社会系统)的绩效或绩效不足。在这种情况下,我们对从个人到社会的跨尺度行为感兴趣。尽管尺度范围很广,但从基本物理学的角度来看,这些都是大尺度行为。
因此,我们可以比较不同类型的组织,如基于个人执行独立任务的组织或具有协同行为的大型协同组织。Ashby定律的多尺度版本现在成为这样一个命题,即大尺度任务需要以协调方式行动的大型团队,而相对小(个体)尺度而复杂性高的任务则需要独立的个体来执行不同的任务。这在大规模军事对抗与普通诊疗之间的对比中显而易见。1991年2月24日至28日,海湾战争期间,地面部队成千上万的人以协调方式运动。普通医疗服务中数十万名医生对情况各异的个人进行医疗诊断。认识到不同类型任务的区别以及组织结构与执行不同任务需要之间的关系,是成为制定管理组织结构原则的基础。
我们可以推断出结构与功能之间关系的一般分析,特别是中央控制结构对执行高度复杂的集体任务的局限性 [14],这种局限是因为层次结构限制了在层次结构的子部分之间传递信息的范围和程度。
我们可以获得一些更具体的见解 [131],包括认识到现代医疗服务财务管理策略与医疗系统向个人提供小尺度复杂护理的能力是背道而驰的 [130],这是其无法提供高质量服务的根本原因。同样,教育系统通过集中的标准化测试无法使其行为与个体的异质性相匹配。在军事环境中,常规部队不可能成功地对高度复杂的军事遭遇做出反应,而进行因人而异训练的海军陆战队员们会有更好更有效的应对。同样,常规的瀑布过程 [133] 也无法通过层次分解来解决复杂的工程项目。
这些结果可以从不同系统复杂度曲线的一阶特征得出,它们反映了旨在执行不同任务的社会系统的整体功能。复杂度曲线在此类系统上的更细节的定量应用是可能的。使用多尺度信息论和Ashby法则的多尺度版本,若发现组织结构与任务之间存在明显的不兼容性,就可以得到结构性无效的基本见解。
我们可以预期,复杂系统的模型构建将需要大量的理论和实证工作来进行验证。只是构建出模型是不够的,还必须分析其捕捉系统行为的能力以及对精细尺度细节的稳健性。识别其通用类以及对相关参数的依赖性是困难的,这些是技术上的难题,需要认真对待。
我们为什么不包括更多细节?如果我们包含的足够多,模型是否正确?答案是否定的,原因有两个。第一个理由就很充分,但第二个更重要。第一个原因是,包含许多细节而不确定什么是重要的什么是不重要的,无法告诉我们是否已包含重要的细节。第二个原因是,包含许多无关紧要的细节实际上会妨碍我们解决真正要回答的问题:哪些杠杆(levers)很重要?确定杠杆很重要,就是相当于确定大尺度上什么是重要的。因此,我们真正想回答的关于系统的问题就是确定哪些是相关变量。
因此,这个困难过程是无法回避的。大尺度可靠模型的构建使得现象学的投资能够在解决关键问题的能力上取得成效。因此,努力构建这些模型是很重要且值得去做的事情。
以这种方式考虑系统时,我们应该认识到,无论是从理论还是现象来看,用文字、图片、电影、数字或方程式描述或表征的任何数学模型都“有效”(valid)的而与细节无关(irrelevance of details)。而且,由于模型的表示已经捕获了重要变量,这种信息可以适用于不同的实例。我们观察的的任何两个系统(或同一系统在不同时间或同一系统的不同情况)在细节上会有不同。如果我们想说关于系统任何有意义的事情——从科学的可重复性或知识的实用性意义上说——唯一重要的就是具有普适性的描述,即独立于细节。对于仅在特定实例中正确的信息是没有效用的。因此,所有科学探究都应被理解为对普适性的探究——来确定信息的一般性或具体性的程度。
IX. 补充材料:技术要点
(APPENDIX: TECHNICAL POINTS)
尽管本文不打算回答“该如何做”的问题,但总体上有一些与应用相关的技术要点。此外,应用策略也可以用更一般的方式来制定。
将大尺度行为分析方法应用于复杂的物理、生物和社会系统的关键之一是认识到在较大的观察尺度上识别系统的可区分状态的重要性,并与我们描述系统的观测尺度保持一致,即我们可以在描述中允许不确定性或误差的水平。在这方面的技术问题是由于倾向于使用实际数量,而没有识别它们所代表的不同状态的数量或不同变量的相对大小。这在代数变换中常用。例如,我们经常认为y或log(y)或ey或1/y是同等有效的变量。但是,这样的变换会改变变量在不同值处的不确定性大小。因此,使用真实数据而没有具体弄清不确定性以及不确定性如何取决于变量的值(如枚举变量的可区分值)会掩盖我们试图捕获的内容。
第二个关键是了解聚合(aggregation)的工作原理。随着我们提升尺度,或等效地,降低我们对系统观测的分辨率,我们看到的细节越来越少。较小的区别消失了,只有涉及系统许多部分的较大区别仍然存在。属性如何聚合决定什么(重要的)会被观察到。使用事物聚合的内在方式使我们能够确定系统的哪些属性在更大尺度上很重要。聚合方式取决于各个部分如何相互依赖。最简单的情况是它们完全依赖或独立。在这种情况下,聚合是从统计数据得出的平均,会产生正态(高斯)分布。当元素相互依赖时,由于受同一事物的影响或相互影响。N个元素的聚合的尺度就是系统规模N。当它们完全独立时,聚合尺度将是系统规模的平方根√N。理解其他类型的系统及其尺度行为的关键在于,由于交互作用,约束和动力学而使得组元之间存在依赖关系,最终导致系统产生跨尺度的行为。
第三个关键是认识到有一种通用的方式来表示系统的行为。任何系统都可以分解为组元,构建模型的重要方式是:在组元的依存关系得到适当解释的情况下,理解组元行为是如何聚合构成整体行为的。需要了解的有关组元的重要属性就是组元所具有的一组可区分状态集合。同样,需要了解的有关整个系统的重要属性也是系统具有的可区分状态集合。此外,我们需要知道外部影响如何耦合到这些状态。因此,模型构建的过程是:(a)确定要描述的系统的元素集合;(b)确定它们具有的可区分状态集合;(c)确定这些状态之间的依赖关系;(d)分析整个系统的可区分状态,它们是由组元的可区分状态及其依存关系引起的;(e)描述外部力量对系统可区分状态集的影响。
由于现在系统分析中普遍使用微积分和统计,因此我们必须提防这些近似方法的不当使用。在这些近似中,有关于哪些变量是描述系统的正确变量是特定假设,以及在分析问题时显式或隐式使用平均值和平滑度。此类假设应视为是近似,例如平均场近似(假设所有组元均受相同的环境条件影响)。这种近似使我们回到微积分和统计的平稳性和独立性,这通常被认为是有效的,但是当系统在空间或时间上的存在行为模式导致局部环境存在差异时,这种近似是无效的,需要补充变量。同时,我们绝不能犯以下错误:考虑获取有关系统的“所有数据”,或在没有进行分析哪些信息是真正重要的情况下,就事先确定要使用的系统描述。任何此类工作都是不完整的的,因为它受到可用信息的性质的限制。
考虑可区分的生物学上的例子:细胞的状态,器官的状态,生理状态。任何模型都必须首先识别确定哪些是可区分的状态。这个工作应该在与观察有关的宏观尺度范围内完成。这并不容易,但仍然比描述所有精细细节的问题容易一些。为了确定组织的行为,我们需要确定细胞的可区分状态以及这些可区分状态之间的相互作用。我们不去确定细胞功能的所有细节,只确定可区分的状态。同样,要为社会中的人类建模,我们只需要确定可区分的人类行为状态。可能存在很多与具体个人状态有关的因素,但是这些因素都是不相关的,除非我们正在详细考虑一个人。这就是一个用于复杂系统行为建模的完全通用的框架。
但是,最终要进行的分析的关键是确定信息的尺度(规模):多少个组元在做同一件事。科学问题是要了解是什么控制了多少人在做同样的事情。解决这一关键问题就要确定以下几个方面:
-
作用于系统的外力,它们的强度和影响系统的方式。限制这种影响的障碍/边界会所起的重要作用,以及确定直接作用的组元。
-
影响、传染、模仿、放大以及恢复的内在机制会促使做同一事情或者耦合事情的组元数量的生长变化。组元在一、二或三个空间维度上或更一般地在网络中相互连接的方式通常很重要。同样,组元之间的影响可以是简单地增强,或相反或者其他形式的耦合。
-
噪声及其在触发新行为、独立性和耗散性方面的作用。噪声可以被认为是满足与精细尺度行为相关的传统统计假设的一种外力。单个事件通常被近似为具有局部的和小规模的影响,而独立事件通常被认为是会遍及整个系统而直接影响所有组元的事件。
由大尺度外力引起的孤立事件,其规模增长轨迹是体现出级联效应。噪声事件影响的累积通常是幂律(分形)标度行为的关键。当影响在某个距离上增强而在更大距离上反增强时,就会发生空间格局模式。如果是表现在事件的变化上就会形成振荡。识别发生的特定行为成为一项任务,它只描述外部力量、内部机制和噪声这几个关键方面。
“从大数据到重要信息(From Big Data to Important Information)”是NECSI(新英格兰复杂系统研究所New England Complex System Institute)创始人及所长Yaneer Bar-Yam教授在2016年发表的文章,刊出在复杂性研究方面重要的国际刊物《Complexity》上。本文可以算是“复杂系统科学及其应用的简介(Introduction to the Modeling and Analysis of Complex Systems)”的姊妹篇,内容上稍微深入难懂一些。本文适合阅读“简介”一文对复杂系统科学进行基本了解后的进一步深入了解。
本文由陈清华和高晓慧翻译,沈忱和刘培源审校。陈清华工作于北京师范大学系统科学学院,现为Brandeis大学和NECSI访问学者。本翻译工作得到中国国家留学基金支持。高晓慧现为山西财经大学统计学专业学生;沈忱现工作于NECSI,为研究员;刘培源工作于集智俱乐部。感谢Yaneer Bar-Yam教授同意我们翻译此文,也感谢集智俱乐部协助的翻译和传播工作。
需要特别说明的是,原文中有些词语,如complexity、size、breakdown、independent等都是文章中重要概念,意义丰富,译者感觉很难用某个具体的汉语词汇表达,在不同的地方会用不同的词。此外,译者觉得的一些重要的词汇或者句子附上了英文原文。原文致谢部分没有翻译。
自创建以来,NECSI一直关注复杂系统科学的理论及应用研究。NECSI的近期研究主要围绕物理、社会经济和生物三个大系统及其耦合展开,具体包括复杂网络,基于多主体的建模,多尺度分析和复杂性,混乱和可预测性,演化,生态,生物多样性,利他主义,系统生物学,细胞反应,医疗保健,系统工程,谈判,军事冲突,种族暴力和国际发展等众多领域。NECSI还致力于复杂性科学方面社会服务,包括培训和项目合作。由NECSI主办的第十届国际复杂系统学术会议将于2020年7月26日-31日在美国新罕布什尔州(NH)纳舒厄(Nashua)举行,会议主页https://necsi.edu/iccs-2020。更多其他信息请访问https://necsi.edu。
[1] Bar-Yam, Y. Dynamics of Complex Systems. Perseus Press: Reading, 1997.
[2] Sayama, H. Introduction to the Modeling and Analysis of Complex Systems, Open SUNY Textbooks, Binhamton University, 2015.
[3] Domb, C. The Critical Point: A Historical Introduction To The Modern Theory of Critical Phenomena. Taylor & Francis: London, 1996.
[4] Levelt Sengers, J.M.H.; Greer, S.C. Thermodynamic anomalies near the critical point of steam. Intern J Heat and Mass Transfer 1972, 15, 1865-1886.
[5] Wilson, K.G. Renormalization group and critical phenomena. Phys Rev B 1971, 4, 3174-3205.
[6] Wilson, K.G. Problems in physics with many scales of length. Sci Am 1979, 241, 140-157.
[7] Kadanoff, L. Scaling, universality and operator algebras. In: Phase Transitions and Critical Phenomena, Vol. 5a; Domb, C.; Green, M.S., Eds.; Academic: New York, 1978; pp 1-34.
[8] Nelson, D.R. Recent developments in phase transitions and critical phenomena. Nature 1977, 269, 379-383.
[9] Kardar, M. Statistical Physics of Fields. Cambridge University Press: Cambridge, 2007.
[10] Greer, S.C.; Moldover, M.R. Thermodynamic anomalies at critical points of fluids. Annu Rev Phys Chem 1981, 32, 233-265.
[11] Heller, P. Experimental investigations of critical phenomena. Rep Prog Phys 1967, 30, 731.
[12] Kadanoff, L.P.; Götze, W.; Hamblen, D.; Hecht R.; Lewis, E.A.S.; Palciauskas, V.V.; et al. Static phenomena near critical points: Theory and experiment. Rev Mod Phys 1967, 39, 395-431.
[13] Landau, L.D. Men of Physics: L.D. Landau, Vol. 2; ter Haar, D., Trans.; Pergamon: Oxford, 1969.
[14] Bar-Yam, Y. Multiscale variety in complex systems. Complexity 2004, 9, 37-45.
[15] Bar-Yam, Y. Multiscale complexity/entropy, Advances in Complex Systems 2004, 7, 47-63.
[16] de Gennes, P.G. Scaling Concepts in Polymer Physics. Cornell University Press: Ithaca, 1979.
[17] Kardar, M.; Parisi, G.; Zhang, Y.C. Dynamic scaling of growing interfaces. Phys Rev Lett 1986, 56, 889-892.
[18] Metzler, R, Bar-Yam, Y, Kardar, M. Information flow through a chaotic channel: prediction and postdiction at finite resolution. Physical Review E 2004, 70, 2, 026205.
[19] Mandelbrot, BB, The fractal geometry of nature. Macmillan, 1983.
[20] Peng, CK, Buldyrev, SV, Goldberger, AL, Havlin, S, Sciortino, F, Simons, M,Stanley, HE, Long-range correlations in nucleotide sequences. Nature 1992; 356, 6365, 168-170.
[21] Peng, CK, Havlin, S, Stanley, HE, Goldberger, AL. Quantification of scaling exponents and crossover phe-nomena in nonstationary heartbeat time series. Chaos: An Interdisciplinary Journal of Nonlinear Science, 1995; 5, 1, 82-87.
[22] Mantegna, RN, Stanley, HE. Scaling behaviour in the dynamics of an economic index. Nature 1995; 376, 6535, 46-49.
[23] Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev Mod Phys 2002, 74, 47-97.
[24] West, G.B.; Brown, J.H.; Enquist, B.J. A general model for the origin of allometric scaling laws in biology. Science 1997, 276, 122-126.
[25] Bettencourt, L, West, G, A unified theory of urban living. Nature 2010; 467, 7318, 912-913.
[26] Turing, A.M. The chemical basis of morphogenesis. Bull Math Biol 1990, 52, 153-197.
[27] Lengyel, I.; Epstein, I.R. Turing structures in simple chemical reactions. Acc Chem Res 1993, 26, 235-240.
[28] Werner, E. All systems go. Nature 2007, 446, 493-494.
[29] Kondo, S.; Miura, T. Reaction-diffusion model as a framework for understanding biological pattern formation. Science 2010, 329, 1616-1620. doi:10.1126/science.1179047.
[30] Sussman, G.J.; Wisdom, J. Chaotic evolution of the solar system. Science 1992, 257, 56-62.
[31] Fisher, R. A., The Genetical Theory of Natural Selection (Clarendon Press, Oxford, 1930).
[32] Dawkins, R., The Selfish Gene, 2nd ed. (Oxford University Press, 1989) p. 86.
[33] Whiteley AR, Bhat A, Martins EP, et al. Population genomics of wild and laboratory zebrafish (Danio rerio). Molecular Ecology. 2011;20(20):4259- 4276. doi:10.1111/j.1365-294X.2011.05272.x.
[34] Coe TS, Hamilton PB, Griffiths AM, et al. Genetic variation in strains of zebrafish (Danio rerio) and the implications for ecotoxicology studies. Ecotoxicology. 2009;18:144?50.
[35] Brown AR, Bickley LK, Le Page G, Hosken DJ, Paull GC, Hamilton PB, Owen SF, Robinson J, Sharpe AD, Tyler CR. Are Toxicological Responses in Laboratory (Inbred) Zebrafish Representative of Those in Outbred (Wild) Populations?? A Case Study with an Endocrine Disrupting Chemical. Environmental science & technology. 2011 Apr 6;45(9):4166-72.
[36] Miller RA, Austad S, Burke D, Chrisp C, Dysko R, Galecki A, Jackson A, Monnier V. Exotic mice as models for aging research: polemic and prospectus. Neurobiol Aging. 1999 Mar 1;20(2):217-31.
[37] Doebeli, M., Dieckmann, U., Speciation along environmental gradients. Nature 2003: 421, 259?64.
[38] de Aguiar, M.A.M., Baranger, M., Baptestini, E.M., Kaufman, L., Bar-Yam, Y. Global patterns of speciation and diversity. Nature 2009, 460, 384-387.
[39] Wild, G.; Gardner, A.; West, S.A. Adaptation and the evolution of parasite virulence in a connected world. Nature 2009, 459, 983-986.
[40] Wade, M.; Wilson, D.S.; Goodnight, C.; Taylor, D.; Bar-Yam, Y.; de Aguiar, M.A.M; et al. Multilevel and kin selection in a connected world. Nature 2010, 463, E8-E9.
[41] Nowak, M.A.; Tarnitam, C.E.; Wilson, E.O. The evolution of eusociality. Nature 2010, 466, 1057-1062.
[42] Abbott, P.; Abe, J.; Alcock, J.; Alizon, S.; Alpedrinha, J.A.C.; Andersson, M.; et al. Inclusive fitness theory and eusociality. Nature 2011, 471, E1-E4. [43] Bar-Yam, Y. Formalizing the gene-centered view of evolution. Adv Complex Syst 1999, 2, 277-281.
[44] Sayama, H.; Kaufman, L.; Bar-Yam, Y. Symmetry breaking and coarsening in spatially distributed evolutionary processes including sexual reproduction and disruptive selection. Phys Rev E 2000, 62, 7065-7069. [45] Rauch, E.; Sayama, H.; Bar-Yam, Y. Relationship between measures of fitness and time scale in evolution. Phys Rev Lett 2002, 88, 228101.
[46] Werfel, J.K.; Bar-Yam, Y. The evolution of reproductive restraint through social communication. PNAS 2004, 101, 11019-11024.
[47] Stacey, B.C.; Gros, A.; Bar-Yam, Y. Beyond the mean field in host-pathogen spatial ecology. arXiv 2012, 1110.3845 [nlin.CG].
[48] Rauch, E.M.; Bar-Yam, Y. Long-Range Interaction and Evolutionary Stability in a Predator-Prey System. Physical Review E 2006, 73, 020903.
[49] Werfel, J.; Ingber, D.E.; Bar-Yam, Y. Programed death is favored by natural selection in spatial systems. Phys Rev Lett 2015, 114, 238103. doi: 10.1103/PhysRevLett.114.238103.
[50] Prendergast, JR, Quinn RM, Lawton, JH, Eversham, BC, Gibbons, DW, Rare species, the coincidence of diversity hotspots and conservation strategies. Nature 1993: 365, 335-337.
[51] Myers, N., Mittermeier, RA, Mittermeier, CG, da Fonseca, GAB, Kent, J. Biodiversity hotspots for conservation priorities, Nature 2000: 403, 853-858 (2000).
[52] Gaston, K.J. Global patterns in biodiversity. Nature2000: 405, 220-227. [53] Ehrlich, P.R. & Wilson, E.O. Biodiversity studies: science and policy. Science 1991:253, 758-761.
[54] Faith, D.P. Genetic diversity and taxonomic priorities for conservation. Biol. Cons. 1994:68, 69-74.
[55] Amos, W, Balmford, A, When does conservation genetics matter? Heredity 2001:87, 257.
[56] Frankham, R, Lees, K, Montgomery, ME, England, PR, Lowe, EH, Briscoe, DA, Do population size bottlenecks reduce evolutionary potential? Anim. Cons. 1999:2, 255-260.
[57] Allen B, Kon M, Bar-Yam Y. A new phylogenetic diversity measure generalizing the Shannon index and its application to phyllostomid bats. The American Naturalist. 2009 Aug;174(2):236-43. http://doi.org/10.1086/600101
[58] Nee, S, May, RM, Extinction and the Loss of Evolutionary History. Science 1997:278, 692-694.
[59] Crozier, R.H. Preserving the information content of species: genetic diversity, phylogeny, and conservation worth. Ann. Rev. Ecol. Syst. 1997:28, 243-268.
[60] Moritz, C. Defining evolutionarily significant units for conservation. Trends Ecol. Evol. 1994:9, 373-375.
[61] Lim, M.; Metzler, R.; Bar-Yam, Y. Global pattern formation and ethnic/cultural violence. Science 2007, 317, 1540-1544. PMID: 17872443.
[62] Rutherford, A.; Harmon, D.; Werfel, J.K.; Bar-Yam, S.; Gard-Murray, A.; Gros, A.; et al. Good fences: The importance of setting boundaries for peaceful coexistence. arXiv 2011, 1110.1409.
[63] Bray, AJ, Theory of Phase Ordering Kinetics, Adv. Phys. 43, 357 (1994).
[64] Lagi, M,; Bar-Yam, Y.; Bertrand, K.; Bar-Yam, Y. The food crises: A quantitative model of food prices including speculators and ethanol conversion. arXiv 2011: 1109.4859 [q-fin.GN].
[65] Lagi, M.; Bar-Yam, Y.; Bertrand, K.; Bar-Yam, Y. Update February 2012: The food crises: Predictive validation of a quantitative model of food prices including speculators and ethanol conversion. arXiv 2012, 1203.1313 [physics.soc-ph].
[66] Fama, E. Efficient capital markets: A review of theory and empirical work. J Finance 1970, 25, 383-417. doi:10.2307/2325486. JSTOR 2325486. [67] Shiller, R. Irrational Exuberance. 2nd ed. Princeton University Press: Princeton, 2005. ISBN 0-691-12335-7.
[68] De Long, J.B.; Shleifer, A.; Summers, L.H.; Waldmann,R.J. Positive feedback investment strategies and destabilizing rational speculation. J Finance 1990, 45, 379- 395.
[69] LeBaron, B.; Arthur, W.B.; Palmer, R. Time series properties of an artificial stock market. J Econ Dyn and Control 1999, 23, 1487-1516.
[70] Muchnik, L.; Solomon, S. Statistical mechanics of conventional traders may lead to non-conventional market behavior. Physica Scripta 2003, T106, 41-47.
[71] Lux, T.; Marchesi, M. Scaling and criticality in a stochastic multi-agent model of a financial market. Nature 1999, 397, 498-500.
[72] Hommes, C.; Wagener, F.O.O. Complex evolutionary systems in behavioral finance. In: Handbook of Financial Markets: Dynamics and Evolution; Hens, T.; Schenk-Hoppè, K.R., Eds.; North Holland: Amsterdam, 2009; pp 217-276.
[73] Prinz F, Schlange T, Asadullah K. Believe it or not: how much can we rely on published data on potential drug targets?. Nature reviews Drug discovery. 2011 Sep 1;10(9):712-
[74] Ioannidis JPA, Why Most Published Research Findings Are False. PLoS Med 2005: 2(8): e124. doi:10.1371/journal.pmed.0020124
[75] Mobley A, Linder SK, Braeuer R, Ellis LM, Zwelling L. A Survey on Data Reproducibility in Cancer Research Provides Insights into Our Limited Ability to Translate Findings from the Laboratory to the Clinic. Arakawa H, ed. PLoS ONE. 2013;8(5):e63221. doi:10.1371/journal.pone.0063221.
[76] L.P. Freedman, I.M. Cockburn and T.S. Simcoe. The economics of reproducibility in preclinical research. PLOS Biology. Vol. 13, June 9, 2015, p. 31002165. doi: 10.1371/journal/pbio.1002165.
[77] Harmon, D.; Lagi, M.; de Aguiar, M.A.M.; Chinellato, D.; Braha, D.; Epstein, I.; Bar-Yam, Y., Anticipating economic market crises using measures of collective panic. PLoS ONE July 2015, 10(7): e0131871, doi:10.1371/journal.pone.0131871
[78] de Aguiar, M. A. M., Epstein, I., Bar-Yam, Y. Analytically Solvable Model Of Probabilistic Network Dynamics. Physical Review E 2005, 72, 067102.
[79] Albert R, Barabasi AL. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002; 74: 47-97.
[80] Braha D, Bar-Yam Y. From centrality to temporary fame: dynamic centrality in complex networks. Complexity. 2006; 12: 59-63.
[81] Hill SA, Braha D. Dynamic model of time-dependent complex networks. Physical Review E. 2010; 82: 046105.
[82] Mantegna RN. Hierarchical structure in financial markets. Euro. Phys. J. B. 1999; 11: 193-197.
[83] Garas A, Argyrakis P, Havlin S. The structural role of weak and strong links in a financial market network. The European Physical Journal B-Condensed Matter and Complex Systems. 2008; 63: 265-271.
[84] Schweitzer F, et al. Economic networks: the new challenges. Science. 2009; 325: 422-425.
[85] Emmert-Streib F, Dehmer M. Influence of the time scale on the construction of financial networks. PloS one. 2010; 5: e12884.
[86] Vandewalle N, Brisbois F, Tordoir X. Self-organized critical topology of stock markets; 2000, arXiv: condmat/0009245.
[87] Bonnanno G, Caldarelli G, Lillo F, Mantegna RN. Topology of correlation-based minimal spanning trees in real and model markets. Phys. Rev. E. 2003; 68: 046103.
[88] Kenett DY, Tumminello M, Madi A, Gur-Gershgoren G, Mantegna RN, Ben-Jacob E. Dominating clasp of the financial sector revealed by partial correlation analysis of the stock market. PloS one. 2010; 5: e15032.
[89] Mantegna RN, Stanley HE. An introduction to econophysics. 1st ed. Cambridge: Cambridge University Press; 2000.
[90] Onnela JP, Chakraborti A, Kaski K, Kertesz J, Kanto A. Dynamics of market correlations: taxonomy and portfolio analysis. Phys. Rev. E. 2003; 68: 056110.
[91] Harmon D, Stacey B, Bar-Yam Y, Bar-Yam Y. Networks of economic market interdependence and systemic risk. arXiv: 2010, 1011.3707v2.
[92] Kenett DY, Preis T, Gur-Gershgoren G, Ben-Jacob E. Dependency network and node influence: application to the study of financial markets. International Journal of Bifurcation and Chaos. 2012; 22: 1250181.
[93] Guillaume DM et al. From the bird’s eye to the microscope: a survey of new stylized facts of the intra-daily foreign exchange markets. Fin. Stoch. 1997; 1: 95-129.
[94] Gopikrishnan P, Meyer M, Amaral LAN, Stanley HE. Inverse cubic law for the distribution of stock price variations. Eur. Phys. J. B. 1998; 3: 139-140.
[95] Chinellato DD, de Aguiar MAM, Epstein IR, Braha D, Bar Yam Y. Dynamical response of networks under external perturbations: exact results, arXiv 2007;0705.4607v2.
[96] Chinellato DD, Epstein IR, Braha D, Bar Yam Y, de Aguiar MAM. Dynamical response of networks under external perturbations: exact results. Journal of Statistical Physics. 2015; 159: 221-230.
[97] Harmon D, de Aguiar MAM, Chinellato DD, Braha D, Epstein IR, Bar-Yam Y. Predicting economic market crises using measures of collective panic, arXiv 2011; 1102.2620 [q-fin.ST].
[98] Majdandzic A, et al. Spontaneous recovery in dynamical networks. Nature Physics. 2014; 10: 34-38.
[99] Bury T. Predicting trend reversals using market instantaneous state. Physica A: Statistical Mechanics and its Applications. 2014; 404: 79-91.
[100] Wolfenstein M. Disaster. 1st ed. Glencoe, Illinois: Free Press; 1957.
[101] Smelser NJ. Theory of Collective Behavior. 1st ed. Glencoe, Illinois: Free Press; 1963.
[102] Quarantelli EL. The sociology of panic. In: Smelser NJ, Baltes PB, editors. International Encyclopedia of the Social and Behavioral Sciences. New York, NY: Elsevier; 2001. pp. 11020-11023.
[103] Mawson AR. Understanding mass panic and other collective responses to threat and disaster. Psychiatry. 2005; 68: 95-113.
[104] Diamond DW, Dybvig PH. Bank runs, deposit insurance, and liquidity. Fed. Res. Bank. Minn. Quart. Rev. 2000; 24: 14-23.
[105] Calomiris CW, Gorton G. The origins of banking panics: models, facts, and bank regulation. In: Hubbard RG, editor. Financial markets and financial crises. Chicago: National Bureau of Economic Research; 1990. pp. 109-175.
[106] Cutler D, Poterba J, Summers L. What moves stock prices? Journal of Portfolio Managment. 1989; 15: 4- 12.
[107] Mann L, Nagel T, Dowling P. A study of economic panic: The “run” on the Hindmarsh Building Society. Sociometry. 1976; 39: 223-235.
[108] Galbraith JK. The Great Crash 1929. 1st ed. New York, NY: Houghton Mifflin; 1954.
[109] Kindleberger C. Manias, panics, and crashes. 1st ed. New York, NY: John Wiley & Sons Inc; 1978.
[110] Sornette D, Johansen A, Bouchaud JP. Stock market crashes, precursors and replicas. Journal de Physique I (France). 1996; 6: 167-175.
[111] Feigenbaum JA, Freund PGO. Discrete scale invariancein stock markets before crashes. Int. J. Mod. Phys. B. 1996; 10: 3737-3745.
[112] Sornette D, Johansen A. Large financial crashes. Physica A. 1997; 245: 411-422.
[113] Sornette D, Stauffer D, Takayasu H. Market fluctuations II: multiplicative and percolation models, size effects, and predictions. In: Bunde A, Kropp J, Schellnhuber HJ, editors. The science of disasters: climate disruptions, heart attacks, and market crashes. New York, NY: Springer;2002. pp. 411-433.
[114] Sornette D. Endogenous versus exogenous origins of crises. In: Albeverio S, Jentsch V, Kantz H, editors. Extreme events in nature and society. New York, NY: Springer; 2006. pp. 95-116.
[115] Bree DS, Joseph NL. Fitting the log periodic power law to financial crashes: a critical analysis, arXiv 2010, 1002.1010v1.
[116] Cho A. Econophysics: still controversial after all these years. Science. 2009; 325: 408.
[117] Feigenbaum JA. A statistical analysis of log-periodic precursors to financial crashes. Quant. Finance. 2001; 1: 346-360.
[118] Sornette D, Johansen A. Significance of log-periodic precursors to financial crashes. Quant. Finance. 2001; 1: 452-471.
[119] Scheffer M, et al. Early-warning signals for critical transitions. Nature. 2009; 461: 53-59.
[120] Scheffer M, et al. Anticipating critical transitions. Science. 2012; 338: 344-348.
[121] Ewens WJ. Mathematical Population Genetics I. Theoretical Introduction. 1st ed. New York, NY: Springer Verlag; 1979.
[122] de Aguiar MAM, Bar-Yam Y. Moran model as a dynamical process on networks and its implications for neutral speciation. Phys. Rev. E. 2011; 84: 031901.
[123] Arthur WB. Self-reinforcing mechanisms in economics.In: Anderson PW, Arrow KJ, Pines D, editors. The economy as an evolving complex system. New York, NY: Westview Press; 1988. pp. 9-33.
[124] Allen, B, Stacey, BC, Bar-Yam, Y. An InformationTheoretic Formalism for Multiscale Structure in Complex Systems. arXiv 2014, 1409.4708.
[125] Mahan, GD, Many-particle physics. Springer Science & Business Media, 2013.
[126] Metzler, R, Bar-Yam, Y, Multiscale complexity of correlated Gaussians, Phys. Rev. E 2005, 71, 046114.
[127] Gheorghiu-Svirschevski, S, Bar-Yam, Y, Multiscale analysis of information correlations in an infinite-range, ferromagnetic Ising system, Phys Rev E 2004, 70, 066115.
[128] Bar-Yam, Y, A Mathematical Theory of Strong Emergence using Multiscale Variety, Complexity 2004, 9, 6, 15-24.
[129] Bar-Yam, Yavni, Harmon, D, Bar-Yam, Yaneer, Computationally tractable pairwise complexity profile, Complexity 2013, 18, 5.
[130] Bar-Yam, Y, Improving the Effectiveness of Health Care and Public Health: A Multiscale Complex Systems Analysis, American Journal of Public Health 2006, 96, 3, 459-466.
[131] Bar-Yam, Y, Making Things Work: Solving Complex Problems in a Complex World, NECSI Knowledge Press, 2005.
[132] Bar-Yam, Y, Global civilization and counterterrorism, CTC Sentinel 2015, 8, 7, 17-22.
[133] Bar-Yam, Y, When Systems Engineering Fails — Toward Complex Systems Engineering in International Conference on Systems, Man & Cybernetics 2003 Vol. 2, IEEE Press, Piscataway, NJ, 2003, 2021-2028.
[134] Bialik, M, Bar-Yam, Y, Beyond big data: Identifying important information for solving real world problems. New England Complex Systems Institute http: //necsi.edu/projects/yaneer/information/
译者:陈清华、高晓慧
审校:沈忱、刘培源
编辑:张希妍
从4710万论文大数据,看科学概念如何演化和传播?
Nature 历年网络科学文集:网络层次和结构
网络科学入门:9大技巧带你上手网络数据分析
Nature 子刊:机器学习高维数据分析中那些一定可以避开的坑!
加入集智,一起复杂!

集智俱乐部QQ群|877391004
商务合作及投稿转载|swarma@swarma.org
搜索公众号:集智俱乐部
加入“没有围墙的研究所”
让苹果砸得更猛烈些吧!
👇点击“阅读原文”,了解更多论文信息




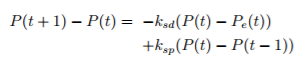 (1)
(1)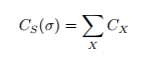 (2)
(2)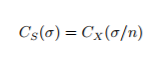 (3)
(3) (4)
(4)











