“集智百科精选”是一个长期专栏，持续为大家推送复杂性科学相关的基本概念和资源信息。作为集智俱乐部的开源科学项目，集智百科希望打造复杂性科学领域最全面的百科全书，欢迎对复杂性科学感兴趣、热爱知识整理和分享的朋友加入！

意大利学者Marco Dorigo从蚁群找最短路径的现象中受到启发，于1992年在博士论文中提出了蚁群算法：一种用来在图中寻找优化路径的概率型算法。此后，蚁群算法不断丰富变化，形成了一个算法家族。有代表性的包括蚁群系统和Max-Min蚂蚁系统等。有趣的是，还有学者在大自然的启发下提出了蜂群、鸟群、鱼群算法等。我们会在以后的集智百科中与大家分享。

一、蚁群算法原理

二、蚁群算法应用

三、蚁群算法优劣

四、相关学者

五、蚁群算法延展

六、相关资源推荐

七、集智百科词条志愿者招募

1、蚁群算法原理

蚁群算法源自对自然界中蚁群觅食行为的深刻观察。科学家发现，蚁群在可以在有障碍物的环境下，找到一条最短到达食物的路径。出现这个现象的原因并非由于某只蚂蚁在指挥，而是依靠整个蚁群的信息传递机制。

这个机制其实很容易理解：蚂蚁在经过的路径上会释放一种气味记号，即信息素。后到的蚂蚁会沿着信息素浓度较高的路径行走。在所有可能的路径中，由于往返最短路径花的时间少，通过频率高，所以信息素浓度高。这又会吸引更多蚂蚁走这条路径，形成正反馈。一段时间后，整个蚁群就会沿着最短路径到达食物了。

每只蚂蚁并不需要知道全局的信息。他们只根据眼前的局部信息，使用简单的规则进行决策。这样，在蚁群集体里，复杂的智能行为会自然涌现。大自然给予我们启示：如果个体都遵循相同的简单规则，就有可能在宏观层面创造出一种集体智慧。

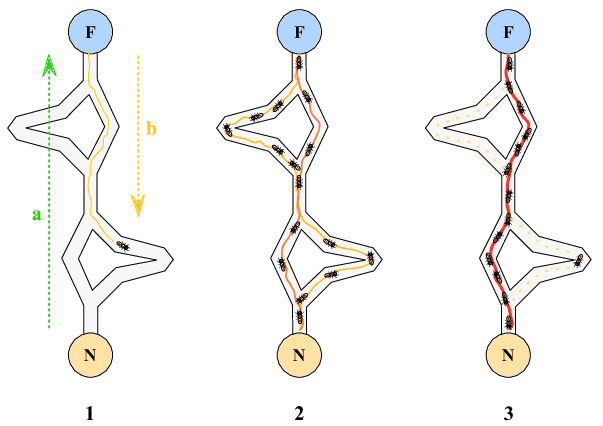
图1：蚁群寻找最短路径机制示意图。N为蚁巢，F为食物。在所有可能的路径中，最短路径上累积的信息素最多。

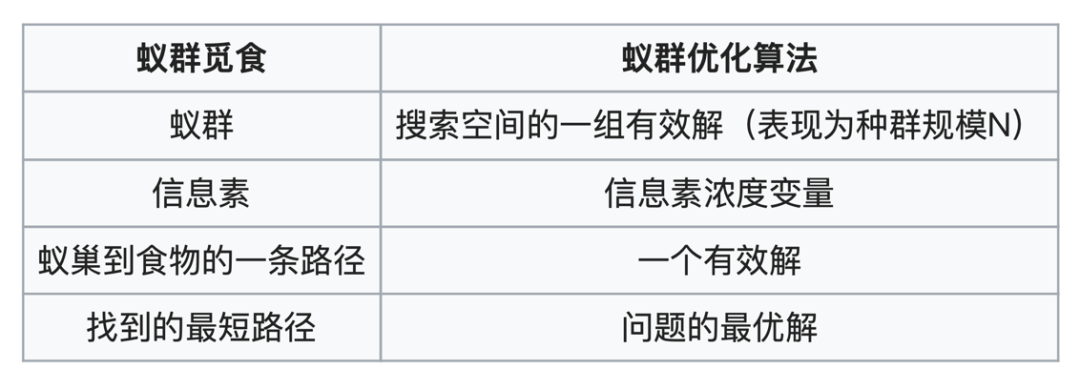
表1：类比蚁群觅食行为对客观世界的算法描述：

2.蚁群算法应用

旅行商问题（Traveling Salesman Problem）

近年来，蚁群算法应用领域不断扩张。可以有效地解决从旅行商问题、指派问题、图着色问题、网络路由问题到车间调度问题、车辆路径问题、分配问题等等。这些问题总结起来主要是NP-hard的组合优化问题，用传统算法难以或者无法求解。此外，在学术界，许多专门针对蚁群算法的会议吸引大量学者参与到蚁群算法的讨论。在商业界，诸如AntOptima之类的专门公司把蚁群算法应用到商业实战中，充分发挥蚁群算法的市场价值。

蚁群算法最经典的应用场景是解决旅行商问题，又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一。

问题：假设有一个旅行商人要拜访N个城市，每个城市只能拜访一次，而且最后要回到开始出发的城市。问商人如何能选择一条满足条件的最短路径？

图3：蚂蚁算法解决旅行商问题。三幅图从左至右分别表示迭代过程、各路径信息素累积量和最短路径。

蚁群算法思路：

将N个城市和城市之间的路径看做一个图。放置m只蚂蚁在图中移动。

寻找最短路径步骤：每只蚂蚁都随机选择一个城市作为其出发城市。蚂蚁依据各路径的信息素值和可见度做出选择，运动到下一个城市。等所有蚂蚁都完成他们的旅行后，找到他们中的最短路径（一个解），此步骤完成。
更新信息素：更新各个路径的信息素数值，包括原有信息素的蒸发和有蚂蚁经过的路径上信息素的增加。
重复上述两个步骤。当达到预定的迭代次数或解不再变化时，算法结束，以当前最短路径作为问题的最优解。

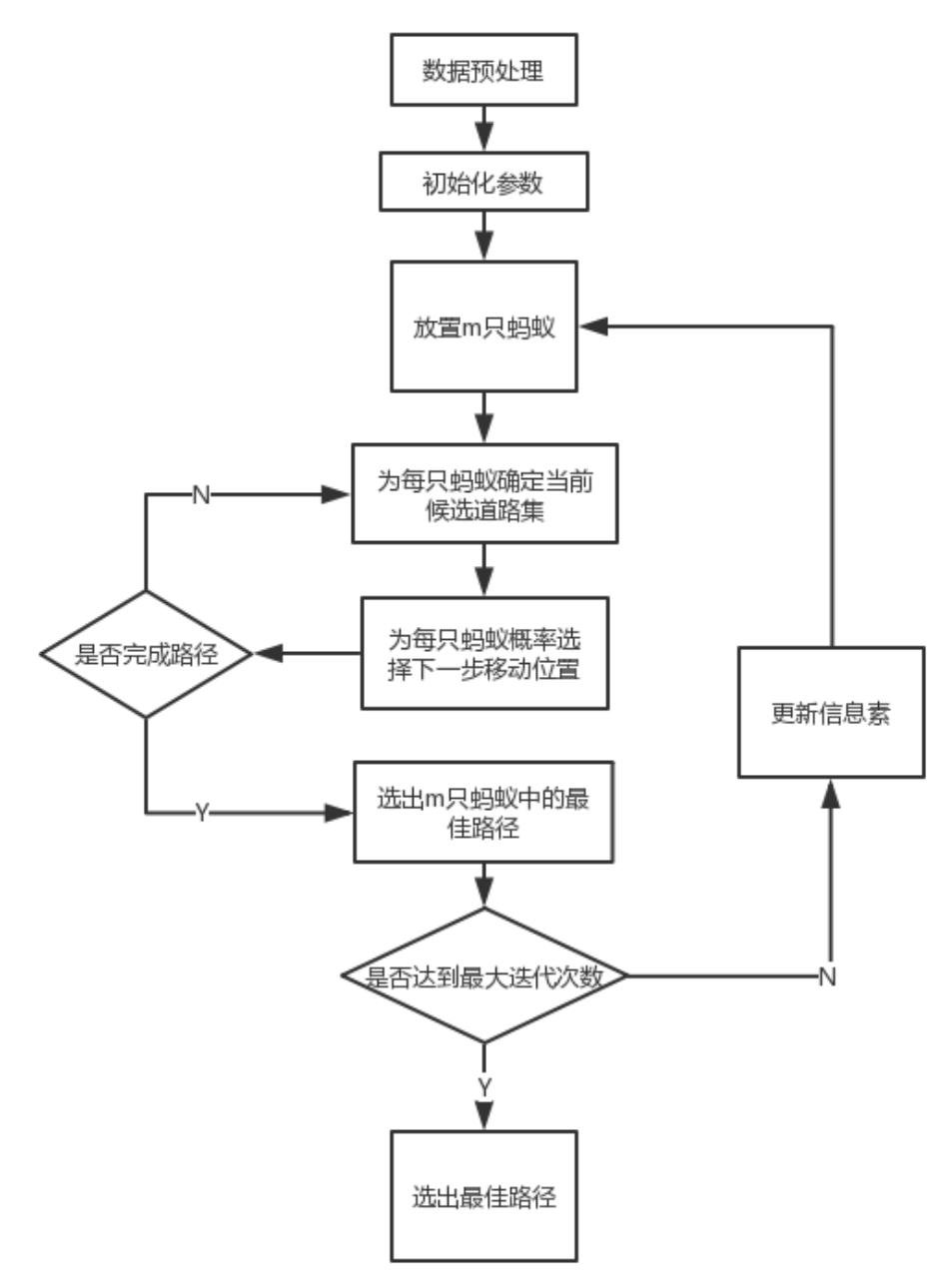
图4：蚁群算法流程图

想亲自动手操作一下的同学，欢迎进入集智百科页面查看解决旅行商问题的蚁群算法Python代码实现：

https://wiki.swarma.org/index.php?title=蚁群算法

3.蚁群算法优劣

蚁群算法的优势：

易获得全局最优解；
应用面广，易于其他问题结合；
分布式计算方式，多个个体并行运算，大大提升了算法的运行效率；
鲁棒性强，采用正反馈机制，使得搜索过程不断收敛，逼近最优解；

蚁群算法的劣势：

虽然一定会收敛，但无法确定收敛所需时间；
理论分析较为困难，算法更侧重于实践层面；

4. 知名学者简介

Marco Dorigo

图5：Marco Dorigo

Marco Dorigo是比利时科学研究基金会（The Belgian Funds for Scientific Research F.R.S.-FNRS）的终身研究员，布鲁塞尔自由大学（Université Libre de Bruxelles）的人工智能实验室IRIDIA的联合主任。

他是蚁群优化元启发式（Ant Colony Optimization Metaheuristic）的发明者，并且是群体智能研究领域的创始人之一。他还是《群体智能》（Swarm Intelligence）的创始编辑和总编辑，《群体智能》是群智能研究领域的核心出版物，致力于报道该学科领域的最新研究和新进展。

Thomas Stützle

图6：Thomas Stützle

Thomas Stützle是比利时科学研究基金会的高级研究员，与比利时布鲁塞尔自由大学的IRIDIA实验室合作。他发表了大量论文。仅在元启发法领域的期刊，会议论文集或经其编辑的书籍中，就超过200篇被同行广泛引用。

Luca Maria Gambardella

图7：Luca Maria Gambardella

Luca Maria Gambardella是一位意大利计算机科学家。他是瑞士提契诺州Manno的Dalle Molle人工智能研究所的所长。他和Marco Dorigo及其他人发表了关于使用蚁群算法解决商旅问题的相关理论研究。

5.蚁群算法延展

蚁群算法提出之后，不断有学者对其进行丰富与变形，形成了一个算法家族。下面是一些常见的变形算法：

蚁群系统 Ant Colony System (ACS)

蚁群系统算法在三个方面进行了改进：

蚂蚁路径选择的规则：更加倾向于选择具有大量信息素的最短路径;
全局更新规则：每次迭代结束后的全局更新仅应用于最优的蚂蚁而非所有蚂蚁；
新增了局部信息素更新规则。

Max-Min 蚂蚁系统 Max-Min Ant System (MMAS)

目前解决TSP问题最好的蚁群算法之一，在蚂蚁系统的基础上进行了如下更改：

每条路径上可能的信息素数量的范围限制在一个区间内；
信息素的初始值被设定为最大信息素量；
只有最短路径上的信息素会增加，其他城市的信息素挥发。

感兴趣的话可以进一步了解其他变体，包括精英蚂蚁系统 (Elitist Ant System)、基于排序的蚁群系统 (Rank-based Ant System)、连续正交的蚂蚁系统 (Continuous Orthogonal Ant Colony)、递归蚁群优化 (Recursive Ant Colony Optimization) 等。