“集智百科精选”是一个长期专栏，持续为大家推送复杂性科学相关的基本概念和资源信息。作为集智俱乐部的开源科学项目，集智百科希望打造复杂性科学领域最全面的百科全书，欢迎对复杂性科学感兴趣、热爱知识整理和分享的朋友加入！

今天分享图论领域里面ER随机图这一主题。如何寻找不确定图之间的联系，发现其之间的规律，本文将介绍ER随机图的基本概念，有哪些好玩的案例，知名的研究者、一些入门的学习资源。


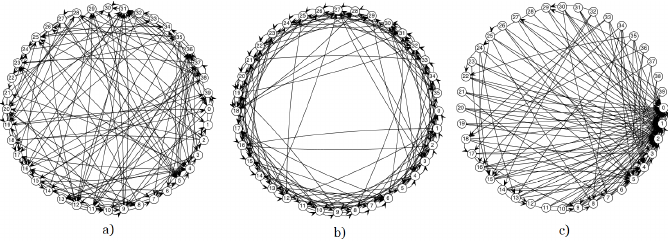
目录


一、什么是随随机图？

二、什么是ER随机图模型？

三、两种ER随机图模型的简单对比

四、ER随机图模型的简单应用

五、知名学者推介

六、相关资源推介

七、集智百科词条志愿者招募



一、什么是随机图？

在了解ER随机图模型（Erdős–Rényi model）之前，我们必须先要了解什么是随机图。对于不了解的图论的人来说这是一个陌生的词汇，但是对于有一定学科背景的人来说，这是图论中的一个基础概念，这也意味着对随机图的掌握是进一步学习的前提。


随机图(random graph)，顾名思义，是由随机过程产生的图，具有不确定性。这一理论处于图论和概率论的交叉地带，主要研究经典随机图的性质。从任一节点出发，按不经过重复节点的规则，可随机走遍所有节点的图称为随机哈密顿图。从任一节点出发，按不过重复边的规则，可随机走遍所有边而回到出发点的图称为随机可迹图。简单理解，随机图是使用一些规则而随机产生的图。ER随机图模型，就是一种提供了一种规则，按照这种规则来产生随机图。

 

 图1：基于随机图模型产生的网络结构


二、什么是ER随机图模型？


ER随机图模型（Erdős–Rényi model）有两个。其名字源于最早提出上述模型之一的数学家保尔·厄多斯（Paul Erdős）和阿尔弗烈德·瑞利（Alfréd Rényi），他们在1959年首次提出了其中一个模型，几乎在同时期，埃德加·吉尔伯特（Edgar Gilbert）独立提出了另外一个模型。


在厄多斯和瑞利的模型中，给定节点和边数情况下产生出任意一种情况的概率是相同的；在吉尔伯特的模型中，每个连边存在与否有着固定的概率，与其他连边无关。在概率方法中，这两种模型可用来证明满足各种性质的图的存在，也可为几乎所有图的性质提供严格的定义。如果这里不太清楚，下面我们对这两种模型进行举例的对比。


三、 两种ER随机图模型的简单对比


1.给定节点数量与边数的ER随机图模型G(n,M)


例如，在G(3，2)模型中，三个顶点和两个边可以构成的三个可能的图，每一个都以1/3的概率包含在内。


2.具有固定节点和连边概率的ER随机图模型 G(n,p)

这种方法是通过随机选取连接节点的方式来产生图。每个边产生的可能都是一个不受其他边影响的概率。该模型中的参数p表示随机两点之间产生边的概率，p可以看作是一个加权函数。当p从0增加到1时，模型越来越多地包含具有更多边的图。拥有n个节点、M个连边的所有图被输出的概率都是。


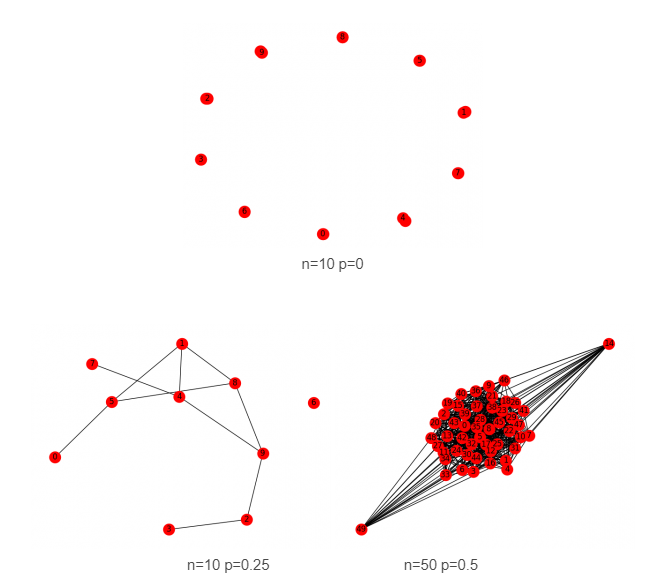
图2：ER随机图模型的简单应用


四、 ER随机图模型的简单应用


随机图模型（不止是ER随机图模型）与现实世界还是很相关的。举一个简单的例子，我们在社交媒体平台微博中随机选取一个用户作为一个节点，将与其互为朋友的用户用边相连接。有研究表明，这种在社交媒体平台形成的网络结构特征类似于随机图。因此，了解随机图有助于我们理解小型社交网络的结构。


更进一步地来说，我们还可以利用实际网络与模型的巨大差异，来识别社交网络中的虚拟账户、AI账户，找到网络中的异常情况。更直接的商业应用是在广告中，利用随机图模型可以发现用户中的商业趋势或识别用户特征，以此实现更精准的广告推送。


五、知名学者简介


保尔·厄多斯 Paul Erdős

图3：Paul Erdős


保尔·厄多斯，匈牙利数学家，因在数论和组合数学方面的工作而闻名，同时他也是一位非常多产的20世纪的数学家。


阿尔弗烈德·瑞利 Alfréd Rényi


图4：Alfréd Rényi


阿尔弗烈德·瑞利，其致力于概率论方面研究，这是他一生中的主要研究课题，但他的兴趣广泛，还涉及统计学，信息论，组合论，图论，数论和分析。


六、相关资源推荐


经典文献


著名的Watts-Strogatz小世界网络模型并未接近总随机化极限的Erdős-Renyi随机图模型，这可能导致混淆并使某些分析复杂化。本文提出了一个简单的替代方案，它不是重连，而是在具有基于距离的连接概率的节点对之间绘制边，并证明了这个模型更容易分析并接近相应极限中的真正的Erdős-Renyi随机图模型。给出了关于度分布，度方差，每个节点的两个星数，每个节点的三角形数，聚类系数和随机游走混合时间的分析结果。


相关阅读：

什么是小世界网络模型 | 集智百科


纪录片

N Is a Number: A Portrait of Paul Erdős


图5：N Is a Number剧照


推荐豆瓣评分9.1的关于我们这篇文章的主人公之一的保尔·厄多斯的纪录片——“N is a Number”。一个只爱数字的男人，因为古怪和多产而著称。豆瓣Clara评论：“为数学而生，为数学活着，最后死在数学研讨会期间，真是可敬的数学家。”
N Is a Number: A Portrait of Paul Erdős播放地址：
https://www.bilibili.com/video/BV1ns411E74Y


课程


复杂的网络与优雅的几何


本课程沿着几何的线路重新梳理复杂网络，包括ER随机网、小世界网络、无标度网络，网络的分形特征等。之后，该课程重点讲述如何利用真实的网络数据来重构系统的空间几何特征。


七、百科项目志愿者招募


作为集智百科项目团队的成员，本文内容由普天星相、Flynn、张江、张朔、宋多多编参与贡献。我们也为每位作者和志愿者准备了专属简介和个人集智百科主页，更多信息可以访问其集智百科个人主页:



以上内容都是我们做这项目的起点，作为来自不同学科和领域的志愿者，我们建立起一个有效的百科团队，分配有审校、翻译、编辑、宣传等工作。我们秉持：知识从我而来，问题到我为止的信念，认真负责编撰每一个词条。


在这里从复杂性知识出发与伙伴同行，同时我们希望有更多志愿者加入这个团队，使百科词条内容得到扩充，并为每位志愿者提供相应奖励与资源，建立个人主页与贡献记录，使其能够继续探索复杂世界。


欢迎扫描下方二维码添加负责人加入集智百科团队！



参考资料：

[1]Erdős, P.; Rényi, A. (1959). “On Random Graphs. I”. Publicationes Mathematicae 6: 290–297. http://www.renyi.hu/~p_erdos/1959-11.pdf.

[2]Bollobás, B. (2001). Random Graphs (2nd ed.). Cambridge University Press. “.ISBN 0-521-79722-5”

[3]E.N. Gilbert (1959). “Random Graphs”. Annals of Mathematical Statistics 30 (4): 1141–1144. “.doi:10.1214/aoms/1177706098”

[4]Newman, Mark. E. J.; Strogatz, S. H.; Watts, D. J. (2001). “Random graphs with arbitrary degree distributions and their applications”. Physical Review E 64: 026118. “.doi:10.1103/PhysRevE.64.026118 .arxiv:cond-mat/0007235 .bibcode:2001PhRvE..64b6118N”, Eq. (1)

[5]Erdős, P.; Rényi, A. (1960). “On the evolution of random graphs”. Magyar Tudományos Akadémia Matematikai Kutató Intézetének Kőzleményei [Publications of the Mathematical Institute of the Hungarian Academy of Sciences] 5: 17–61. http://www.renyi.hu/~p_erdos/1960-10.pdf. 

[6]Matula, David W. (February 1972). “The employee party problem”. Notices of the American Mathematical Society 19: A-382.

[7]Bollobás, B.; Erdős, P. (1976). “Cliques in Random Graphs”. Mathematical Proceedings of the Cambridge Philosophical Society 80 (3): 419–427. “.doi:10.1017/S0305004100053056 .bibcode:1976MPCPS..80..419B”



来源：集智百科
编辑：曾祥轩



推荐阅读


混沌理论 | 集智百科
什么是熵 | 集智百科
什么是元胞自动机？| 集智百科
无标度网络模型开山之作：随机网络中标度的涌现

从复杂网络小世界、无标度、高聚类特性看新型冠状病毒肺炎

加入集智，一起复杂！




集智俱乐部QQ群｜877391004

商务合作及投稿转载｜swarma@swarma.org

◆ ◆ ◆

搜索公众号：集智俱乐部


加入“没有围墙的研究所”

让苹果砸得更猛烈些吧！



👇科学复杂而又美丽，探寻始于一次点击，“阅读原文”，把握更多百科知识信息。