导语

在社交网络中的的人与人之间，生态网络中的动植物之间，都会出现持续不断的合作现象。然而若适应度较高的个体得以存活，为何存在一些物种自愿付出代价帮助其它个体提高适应度了？合作又是如何成为可能的？5月Nature Communications中的论文“时序网络中的合作演化”（“Evolution of cooperation on temporal networks”），通过网络上的模拟实验，对合作的产生受到哪些因素影响，给出了反常识的回答。

论文题目：

Evolution of cooperation on temporal networks

论文地址：

https://www.nature.com/articles/s41467-020-16088-w

1. 何为时序网络

静态网络中，节点之间要么有边，要么没有边。而动态网络如定格动画片一样，允许节点生成与消失。

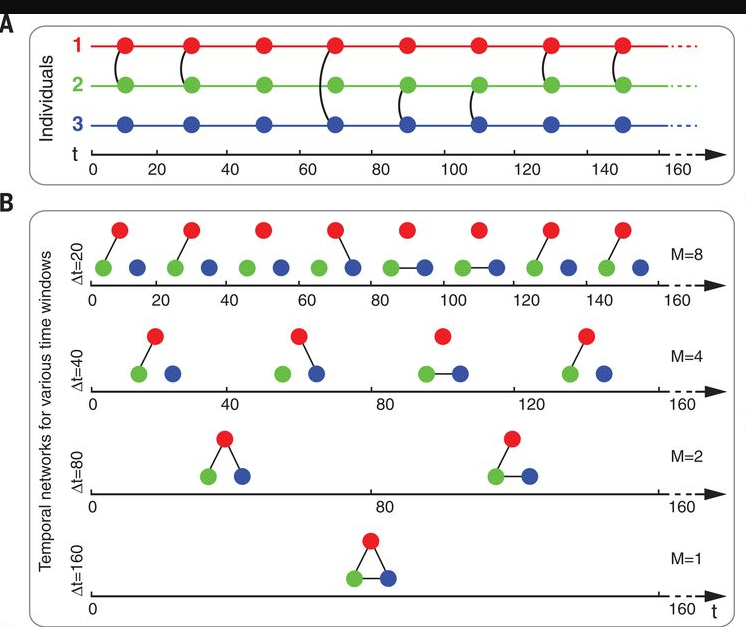
图1：来源：The fundamental advantages of temporal networks 动态网络示意图

上图 A 中描述了三个时序网络节点间的边变化，图 B 中展示了使用不同的时间窗口，能够将一段时间内的时序网络，压缩为一个静态网络，当时间窗口等于网络演化的总时长时，对应的静态网络中，包含了动态网络的全部边。

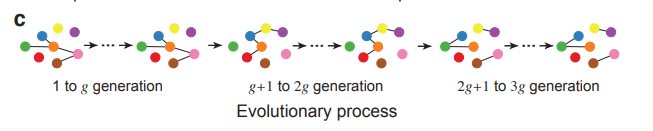
图2：网络演化代数示意图

将时序网络，按照固定的时间窗口压成静态网络，如果网络的结构发生变化，那么就定义为演化过程生成了下一代网络，如上图所示，每一代网络之间的连接模式不同。

传统的关于合作现象的研究，其假设是在合作个体都分布均匀的环境下，在建模时引入网络。这样能够对现实中局部结构有所差异的网络进行建模，通过时序网络这一工具，以相对简单且统一的框架，回答诸如“持续的合作为何会发生？合作过程中每次博弈之间的间隔，合作的频率，对网络中合作者的比例有何影响？个体 A 会先与 B 合作，再和 C 合作，如果 A 被 C 背叛了，那么这一影响，如何对之后 A 与 B 的合作产生影响？”

2. 时序网络上的囚徒博弈

更容易走向合作

图3：囚徒困境示意

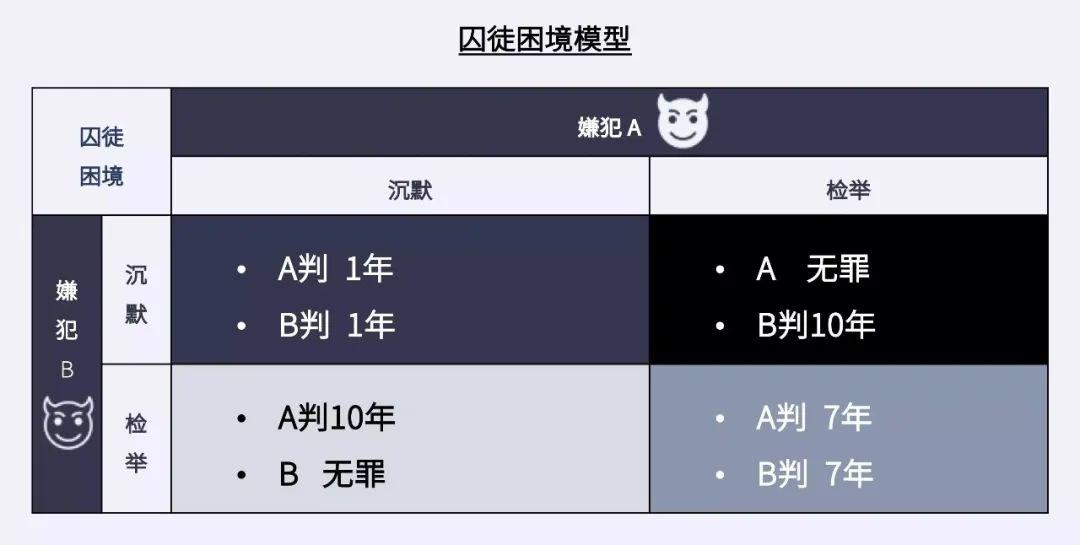
该研究中，在四种真实的网络结构（ACM会议，不同年份的学生之间和办公室间的人际网络）上，模拟节点间随时间展开的囚徒博弈。其中节点按照给定的规则（合作，直到被背叛后选择以眼还眼），随机选择是否与邻近节点展开合作，再根据上一轮合作的收益，决定下一轮是否继续合作或复制周围节点的策略。研究者关注的是不同的合作频率，对合作的模式，即网络中有合作者的比例所产生的影响。

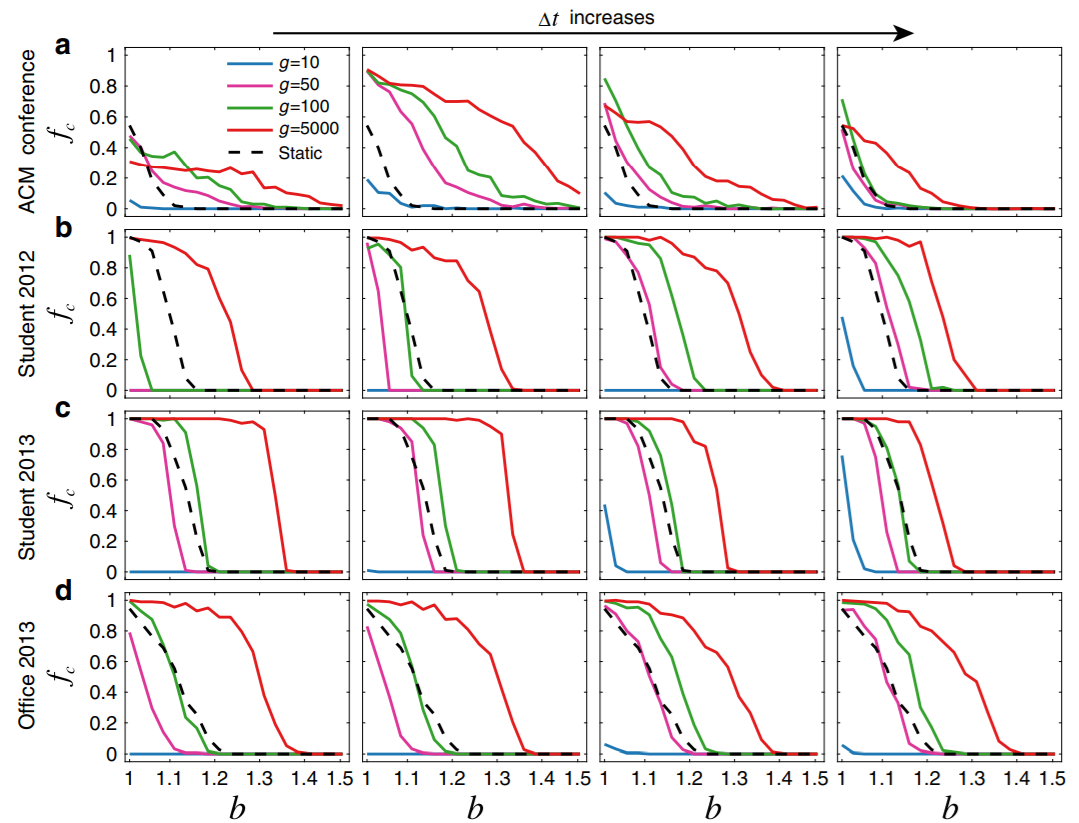
图4：不同真实网络中，合作者比例与时序程度（temporality）及合作背叛收益比的关系

上图中从左到右，代表时间窗口大小逐渐增大；从上到下，代表四种不同的真实网络结构；不同颜色的线条，代表时序网络持续了多少代（图例中的g）。其中黑色的虚线代表只博弈一次的静态网络。横轴的 b 是背叛的收益为合作的多少倍，纵轴是合作者数量占网络中全部节点数的比例。

从图中能够读出下面三条信息，一是如果能够在同样的时间内，以更快的频率交流，即网络的演化代数越多，不管时间如何变化，合作者的比例也越多；二是当合作变的频繁，合作者网络能够在背叛的收益显著高于合作时，仍然保持合作；三是即使合作的频率（g=50或100时）不那么高，网络中最终合作者的比例（图中最右一列），也高于或接近静态网络中的单次博弈。

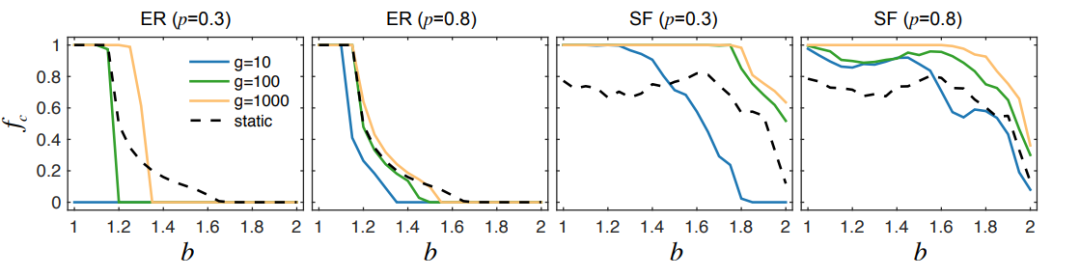
图5：模拟网络中合作者比例，与时序程度及合作背叛收益比的关系

上图反映了在两种常见的模拟网络结构，ER 和无标度网络上，类似的合作者的比例与时间及合作背叛收益比的关系。在更接近真实情况的无标度网络上，可以看到类似的规律。

3. 网络中的随机连接

能够促成合作的发生

前文的发现，即更高频的交流，以及对应的合作次数的增多，能够促成网络中合作者数量的增加，这还是一个相对符合直觉的结论。毕竟我们看着历史上通讯技术的进步，使合作变得越发成为常态。然而问你一个陌生人组成的网络和一个熟人网络，哪一个合作者的比例更高，大部分都会说后者。

然而现实中的合作频率，不是均匀的，而是 80% 的时间进行 20% 的合作决策，而在剩下的 20% 的时间内，密集决定剩下的 80% 次中是否合作。这被称为社交活动具有的突发性（Burstiness）。这样导致在熟人网络中，如果短时间内连续出现多次背叛，那么本来的合作者会永久的变为背叛者，而这在陌生人第一次合作中，并不会出现。

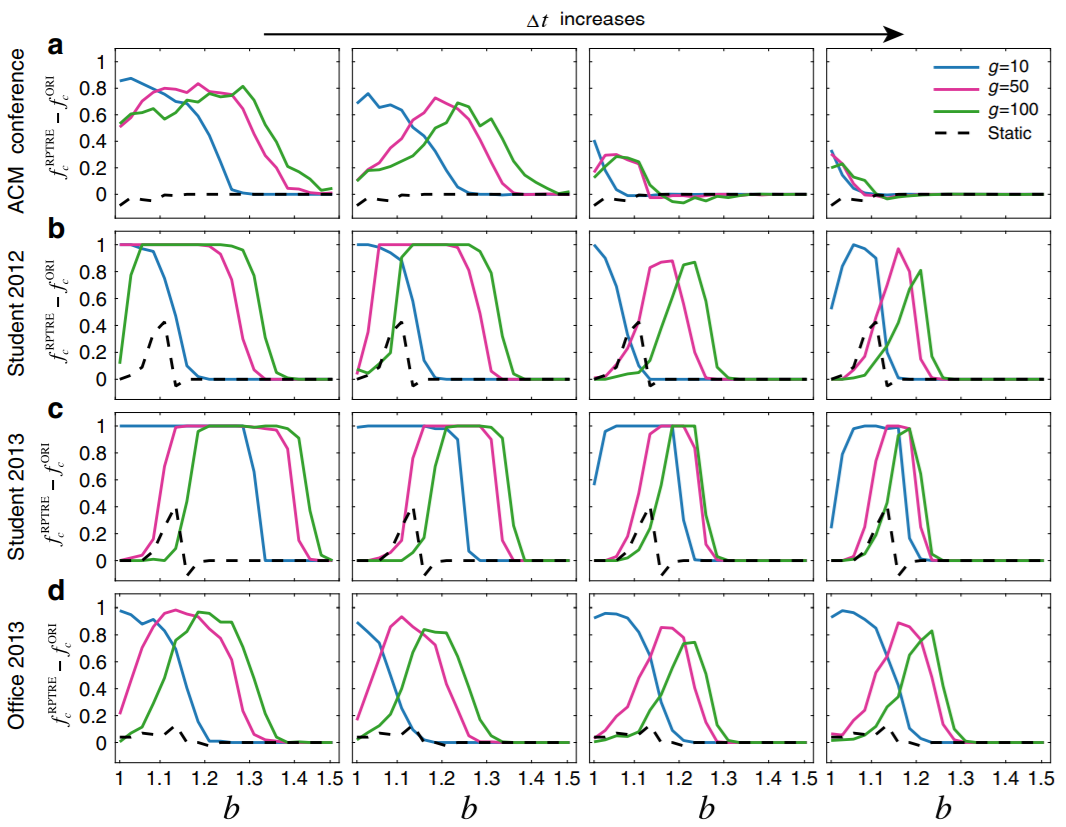
图6：合作者比例在有随机扰动与原始网络中的差异

在网络中引入的随机性，可以分为两类，一类是将节点做决定的间隔时间打乱，这样就不会出现在短时间内做多次决定的场景，第二类是在网络中，随机的增删部分连接，即为图中的 RPTRE。上图与之前图的不同之处，在于纵轴变为了引入随机性之后的网络和不引入随机性网络中，合作者节点所占的比例。可见不管在何种模拟参数中，合作者的比例都有显著增加。

4. 促成背叛发生的因素

满足倒U型曲线

针对合作与时序程度的关系，上面的分析先是说同样时间内交流的越多，合作者比例越多，之后又由于随机的打乱网络的结构和次序，相当于破坏了网络的时序特征。降低了网络的时序属性，而这会导致合作者的比例高于随机情况下的合作者所占的比例。

这一类多了不好，少了也不好的现象，比如金发女孩效应，讲的是唯有在一个恰当好的环境中，金发女孩才能出现，环境中所有的参数既不能太大，又不能太小。最典型的例子是生命的诞生，其需要的环境就很苛刻。

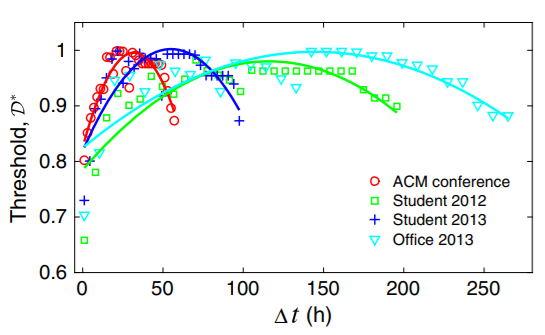
图7：合作者和时序关系间满足金发女孩效应

由此，若将合作受时间影响的程度，用一个统一的变量定义，那么存在一个最优的比例，即倒 U 型曲线，在该比例下，合作者人数所占的比例最高，如上图所示。

5. 合作与群体智慧

及道德的关系

一个群体的成功，取决于群体间的成员能否充分的展开合作。通过该研究的模拟实验，可以做出如下有依据的推测：若想促进群体间的合作，首先需要群体间有足够频繁的交流，不能固定的只是每月一次例会，但也不能交流的太过频繁；其次，要引入随机的连接，并改变交流发生的时间间隔，让网络中两点的交流不是呈现爆发式的，短时间的高频交流以及随之而来的持久的沉默，不利于合作的维持。

这些假设都是能够、也是值得通过管理学实验去验证的，唯有这样，才能用复杂科学将管理学中的经验变为科学发现。

通过时序网络，对合作的建模，还能够解释道德感的出现与不同文化背景下的差异。常听父母辈抱怨世风日下、人心不古。对此现象建模，如果在模型中引入节点的声望，来反映持续博弈带来的影响，不如通过上述的时序网络简单直接。

对于为何在一个动荡的高速发展的环境下，合作者人数在网络中占比会下降，可以解释为背叛的收益相对增加，且新的技术使得合作能够高频展开，从而使网络远离了合作者比例最高的“金发女孩”带。

而当社会经济相对稳定后，合作者的比例又会进入“金发女孩”带中，于是人们又会发觉如今再一次“夜不闭户，日不拾遗”了。