导语

什么样的交流，能够言简意赅地传递信息？通过实验，结合对真实世界的文学、科学、音乐所呈现的网络特征进行的研究，6月15日，发表在Nature Physics的论文“复杂网络中的人类信息处理”，揭示了有效交流需要满足的两个特征。

论文题目：

Human information processing in complex networks

论文地址：

https://www.nature.com/articles/s41567-020-0924-7

1. 如何用网络科学研究人类交流

在人类社会，不管是交谈、写作还是欣赏音乐，这些交流都有共同点，就是他们都可以抽象为一串离散的字符。由此进一步地将这些字符串分为一个个的组件，而后将这些组件作为网络节点，并且将连接这些组件的转折性词句作为网络连边。借鉴这样的思路，我们就通过网络科学的工具来研究人类的交流行动。

之前的研究中，人们关注的是网络本身的复杂度和其存在的规律。然而，不论是语言还是音乐，其唯一的目的就是交流思想与情感，而交流是否高效，取决于接收信息的人如何反应。因此该研究的创新点在于首次用网络科学的工具来研究信息如何被接受，其信息传播过程中会呈现出怎样的规律。

不论是阅读还是交谈，我们的大脑总在不断地，对将要面对的交流内容进行预判，并根据和事实的吻合程度，实时地修正预测。这在认知科学中，这被称为预测编码理论。

另一个和该研究相关的，是集智之前介绍过的最优学习率，即在学习新知识时，15%的未知信息搭配85%的熟悉内容，能够让大脑最高效地吸收新的知识。而本研究的则将问题翻转，即探寻所交流所使用到的质料，需要满足何种结构，才能契合大脑固有的特征，从而使交流更加高效？

在引入网络之前，对于一个字符串中包含了多少信息，量化的指标来自香农提出的“信息熵”。然而该定义描述的是信息产生者所产生意外的多少，而不是信息接收者所获取的信息。使用交叉熵，可以量化信息接收者预期和发送者之间的差异。

2. 大脑对交流的预期比想象的复杂

当我们听到出乎意料的消息时，往往会错愕得说不出话来。本研究的实验部分，通过测量受试者在接到信息和做出行动之间的时间差，来研究大脑在接收信息时，如何对信息进行预期管理。

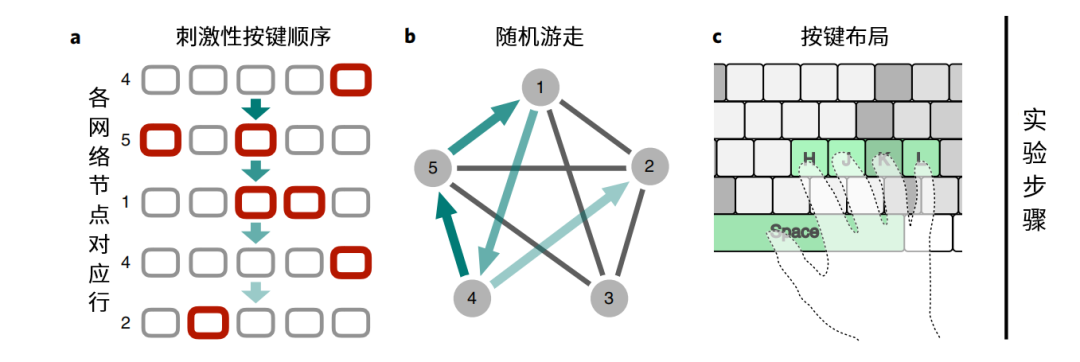
受试者的右手5个手指分别对应键盘的Space、H、J、K、L这5个按键，根据指令按下按键。一共有5组刺激受试者的指令（stimuli），每一组指令要求受试者按下1个或2个标红的按键，如下图a所示。

图1：实验设计示意图

上图a中，可能的按键为5+5×4/2一共15种，每一组指令，看成网络中的节点。网络中节点间的边，代表可以从该节点转换到其他节点，具体的转换顺序由随机游走决定。每名受试者需完成1500次实验。

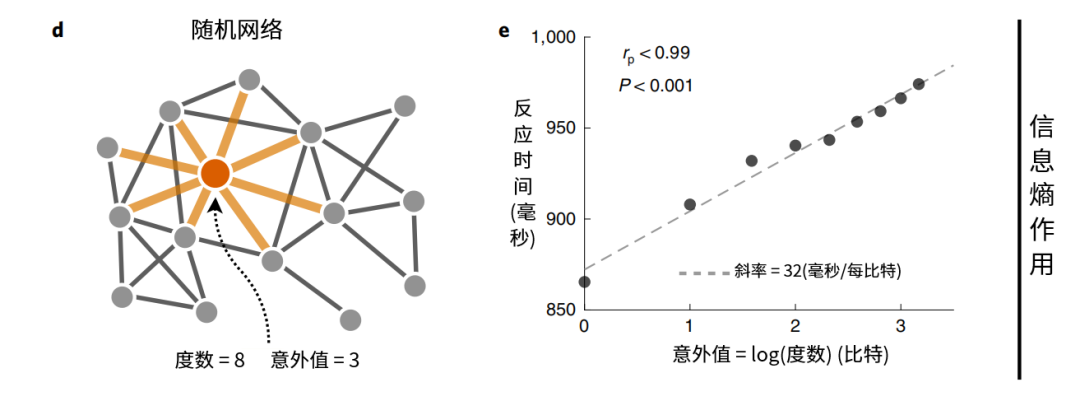
图2：信息熵和反应时间呈正相关

在一个根据ER模型生成的、包含30条边的随机网络中，从点a到点b的信息熵为该点度数的对数，意味着一个节点的度数越高，在随机行走中，从这个点出发，下一个节点就对应越多的可能。因此可以说从这点出发，带来的意外越明显。例如上图左边红色的节点，其度数为8时对应的意外值为3。

由于实验会持续1500次，如果节点a总是连接节点b，那么受试者就能在短期记忆中，存储这一练习。由此节点间不同的信息熵就对应着不同的反应时间。上图右边，横轴为节点的意外值，纵轴为反应时间，该图显示，意外值每增加1，反应时间平均增加32毫秒。

图3：网络中的位置影响信息接收的程度

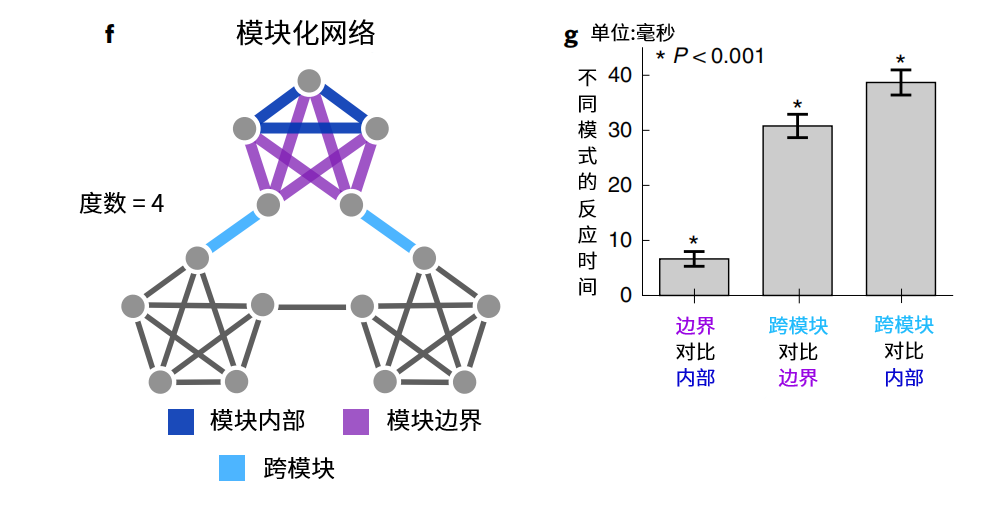
在第二阶段的实验中，网络从随机网络变为了上图左边的网络，图中所有节点，按照前文的信息熵来看，是相同的。然而如果将连接模式分为三类，可以看到不同模式对应的反应时间差异明显（右图）。由此说明，单一的信息熵指标无法反映认知过程的复杂性。

图4：模块化网络示例图

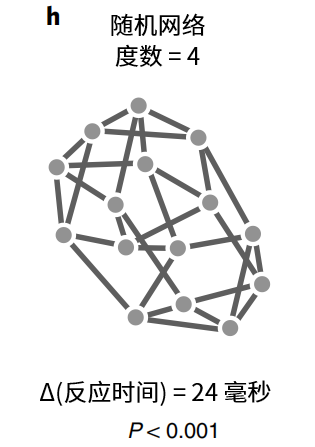
相比平均度数为4的随机网络，上图的网络中，每个节点之间的边，都是对称的，没有哪个节点是特殊的。这样的网络结构被称为模块化网络（modular network）。该网络下的反应时间相比于随机网络平均高24毫秒，说明在该网络下，人脑预期的意外更少、交流更高效。

3. 信息接收者与发送者之间

存在预期差异

图5：信息接收者对传播矩阵的预期

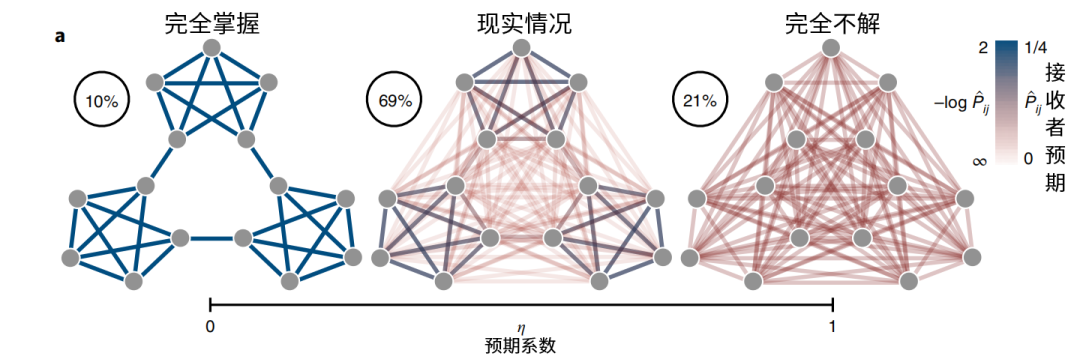
在上述实验中，最初受试者并不清楚网络的结构，因此其对于每个新的按键序列是什么，都是“意外”的。如上图左边所示，图中每条边的颜色，代表受试者对该边的预期。随着实验的进行，受试者对边的预期逐渐变为中间的图，而最左边代表受试者的预期和真实情况完全相同，最右边的图则表示受试者的预期与真实情况完全不同。

用数学的语言来定义，信息接收者预期的概率转移矩阵，也即真实网络中矩阵的交叉熵（等式左边），可以拆分为两部分。一是信息传播者本身的信息熵（等式右边第一项），二是两个矩阵的KL散度（等式右边第二项）。前者是信息传播固有的，后者描述了交流过程中所产生的效率损失。

图6：不同网络结构下交叉熵与预期系数的关系

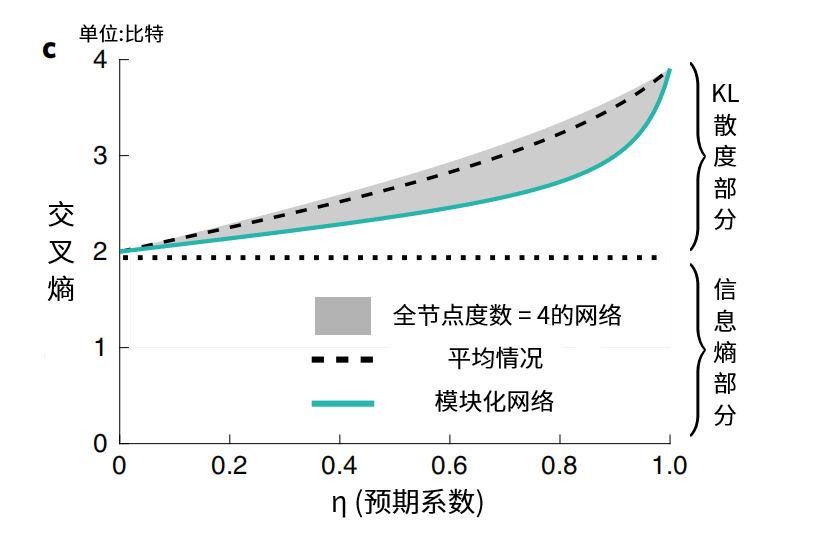
将信息接收者对网络结构的掌握程度，用η来表示，如上图中横轴。对比不同情况下的交叉熵，当接收者完全了解网络的转换方式时，KL散度为0，当完全不知时，交叉熵是最低值的一倍。之所以代表模块化网络的蓝色，能够让受试者的平均反应时间减少24秒，是因为随着η的减少，其交叉熵下降更快，交流中预期和真实不符的情况会更少。

4. 真实网络与随机网络的差别

上述实验，确定了分析工具，部分回答了本文预期要解决的问题，即怎样的沟通是高效的。例如上文的实验中，如果沟通的目的，是让受试者了解网络对应的转移矩阵，那么模块化的网络结构是最优的。然而这和真实世界中的交流，又有何种联系？

图7：李尔王和麦克白的人际网络

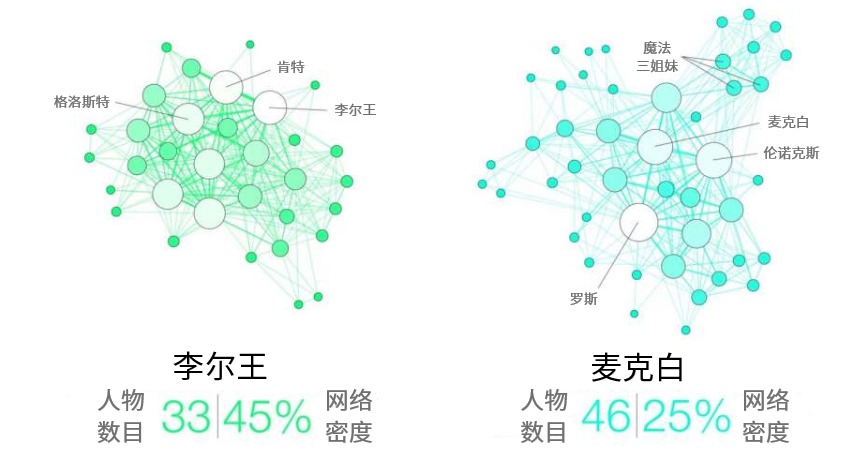
上图是莎士比亚四大悲剧中《李尔王》和《麦克白》对应的人物网络图，网络中的点是戏剧中出现的人物，边代表人物间的交流。上述的真实网络，假设其反映的交流模式是高效的，通过将其与具有相同网络特征的随机网络对比，看两者在上述的分析工具上，例如在交叉熵和KL散度上，有什么不同之处，由此可以揭示出高效交流所具有的特征。

该文研究的真实交流模式，包含了6大类总共40种，分别是传统文学，语义网，互联网，论文引用网络，社交网络，音乐。包含了大部分基于字符串的人类交流模式。

例如将语句中的名词作为节点，将名词间的转折作为边。通过在这样的微观层次进行建模，网络科学使得交流过程中所呈现的结构，得以被量化地研究。

将网络中的连接随机化后，可以计算两个网络对应的转移矩阵之间的KL散度和信息熵。上述6类中，传统文学的信息熵和KL散度都最高，而音乐则两者都相对最低。想想我们阅读柏拉图的名著时，觉得其中文字艰深，对接下来预期的内容也一头雾水；而音乐本来就是用来娱乐的，这也就不难理解了。

上文的实验说明，模块化的网络，能够降低因为交流中预期和实际有所不同所带来的低效。因此可以预期的是，真实的网络也将会具有模块化的特征。例如狗、狼和猫这些词构成的模块中，会有更多的连接，由此使交流更加顺畅。

然而如果交流中只有熟悉的内容，那也是没有什么信息量的。因此高效的沟通，是要在网络的异质性和模块化结构之间找到一个合适的权衡。而真实网络，相比随机网络，同时具有了异质性和模块化结构，从而证明了网络结构对交流效率影响巨大。

5. 三种不同的网络结构，

哪种交流效率更高

下面是一道思考题，交流过程中对应的转移网络接近哪一种，交流效率会最高？

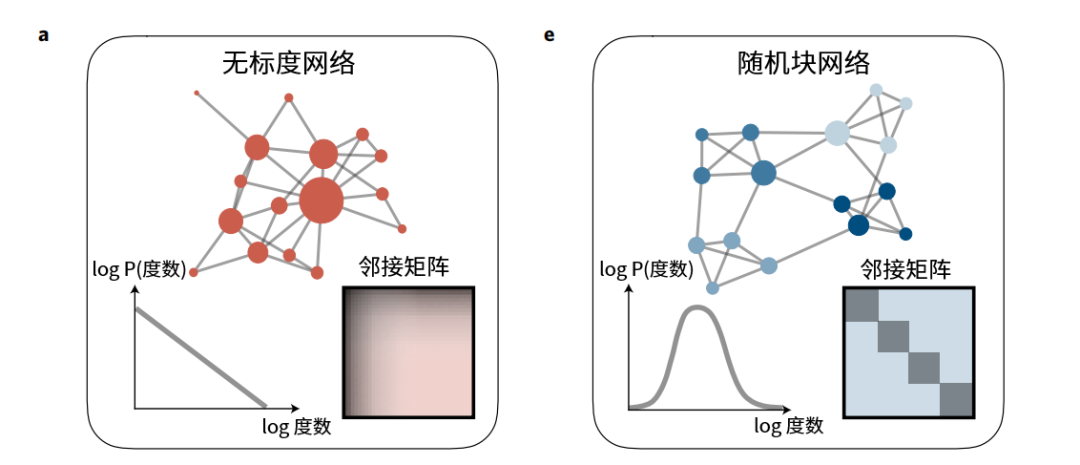
图8：无标度网络，随机块网络，层级化模块网络示例图

上图中第一个是无标度网络，其特点是各网络节点度的分布呈幂律分布。这样的网络中，最常出现的词语对应的连接，是次多词汇的两倍。第二个网络结构是随机块网络（stochastic block network），其中节点的度呈正态分布，每4个节点组成一个组件，组件之类是紧密连接的，而组件之间的连接很稀疏。

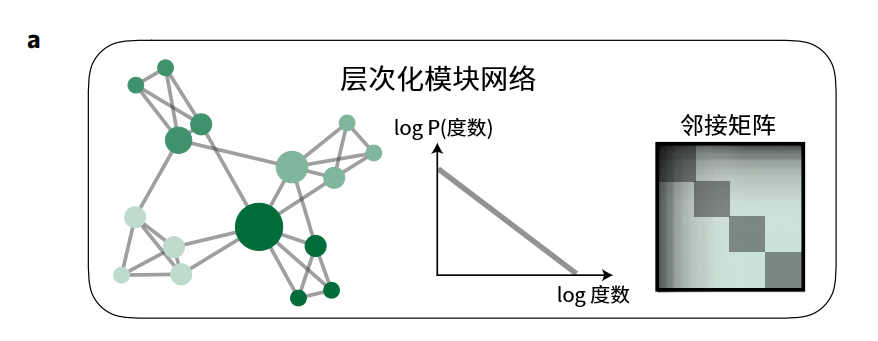
第三种层次化模块网络，其节点分布同样遵从幂律分布，但节点间存在多个小组，因此其对应的邻接矩阵，同时具有了上述两者的特征：即其中包含4个小正方形，且右上角的连接更多。结合上文所述的在异质性和模块化结构之间的权衡，可知该思考题的答案是第三种。

具体对应到现实交流过程中，第一种过度强调核心概念，在讲解时东一榔头西一棒槌，导致网络的模块化程度太低，接收者会难以找到对下一个话题的预期；第二种将观点拆分成了几块，每块分别讲透，但没有重点，模块之间也没有过渡，接收者会觉得缺乏信息量。

而最好的交流，是将核心概念拆分后，按照轻重缓急，分块讲清楚。这样读者就不会觉得这一部分新概念太多难以理解，也能感到每阅读一节，都能带来新的意外，由此使沟通最为高效。定量来看，就是相比随机网络，信息熵的差更大，KL散度的差更小。

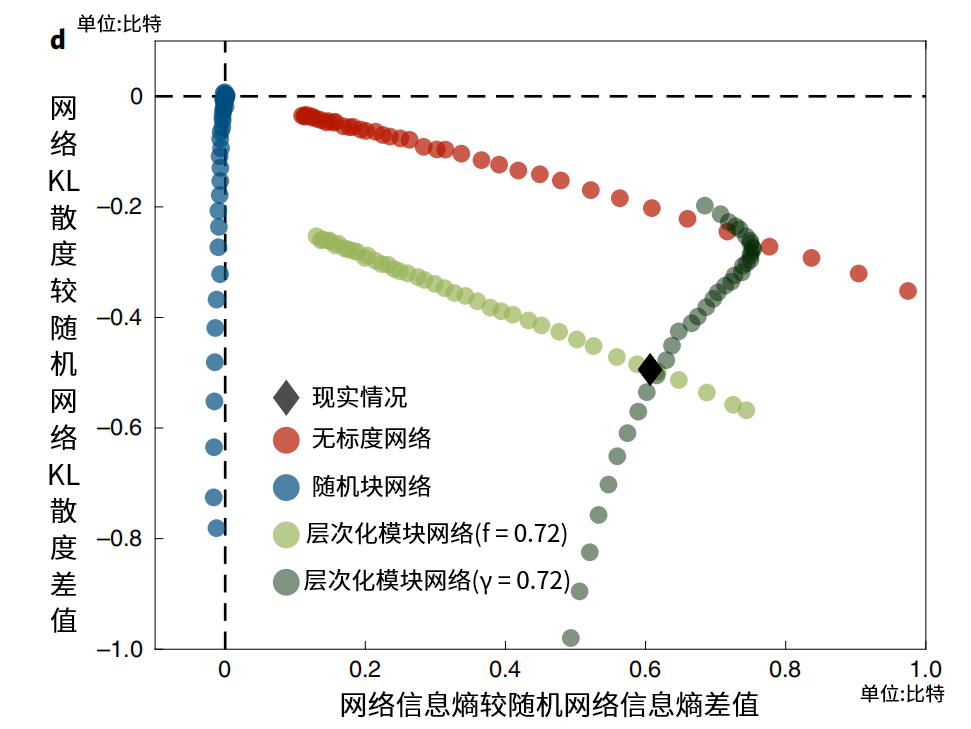
图9：三种网络结构下，真实和模拟的信息熵和KL散度之差

上图中，横轴代表的信息熵之差，代表了该网络能传递的“意外”相比随机网络差距有多少。这个值越大，说明该网络结构对应的交流模式，能够承载更多的信息。纵轴代表的KL散度之差，代表了相比随机情况，该交流模式，避免了多大程度的低效沟通或学习障碍。

图中表现最好的，无疑是浅绿色代表的层级化模块网络。图中黑色的菱形对应的真实网络，正好落在了两种不同参数的层级化模块网络的交点处，说明真实网络的形成遵循层级化模块网络的生成方式，在模块化和异质性之间，找到了最佳的权衡。

将该文的研究结果，应用到生活中。假设你在准备一个十分重要的演讲，你可以将要传递的观点，分解成几个关键词，再将每个关键词进一步拆分，植入到你的思维导图中：每一个节点代表一句话，每个节点包含几个关键词。之后你可以通过调整词句的顺序，使得相邻的自然段之间具有高内聚性，同时让最重要的核心词和每个模块都能建立连接。

在设计人际交互界面时，同样可以依据本文提出的框架，来定量地考察何种交流模式更为高效。例如APP的界面上，如何让主界面上的按钮彼此有所不同，同时在每个子菜单之间的按钮相互有紧密的联系。

人类的交流模式，为何会呈现出本文所发现的规律？是否和大脑本身的结构有关，两者如何共同进化？这是基于本文的研究，需要进一步研究和回答的问题。除此之外，本研究假设交流中的规律符合马尔可夫链的齐次性假设，即不存在概念间的长程连接。然而现实中并非如此，随着认知科学的进步，非马氏的人类交流存在何种规律也是值得研究的。