导语

质数的产生并不随机，依照本文介绍的方法，我们可以将质数映射为图形。巧妙的是，这个图形不但有着美妙的分形结构，而且图形信息和最大公约数序列几乎相同，这意味着我们在寻找质数背后的深层次规律上又迈进了一步，数学的统一之美也再次得以体现。

1.用质数产生有趣的分形图像

今年初，软件工程师Shaun Gilchrist在读了我多年前的一篇博客文章之后，向我伸出援手，与我一起进一步探索质数中隐藏的模式。

乌兰螺旋线揭示了质数的非随机模式，但这种模式和质数匹配并不十分严格。长期以来，Shaun和我都觉得有一个更好的方法来描述这些质数遵循的排布模式，这或许会揭示出一个更深层次的结构。

乌兰螺旋线指的是，将正整数按逆时针螺旋排列，再将其中的质数标出，我们会发现质数的排布并不是完全随机的，甚至有时会按照直线排布。

如下图，质数是被标红且背景取为灰色的区域。

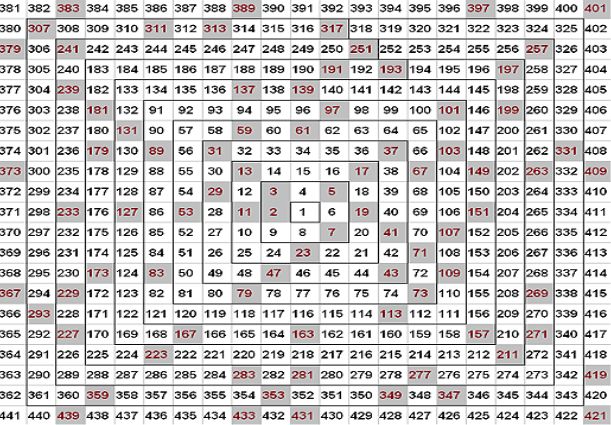
Shaun 解释说，他开发了一种新的算法 (他称之为”视差压缩”) ，这个算法会在二维平面上将质数进行“包装”，并在乌兰螺旋的启发下可视化它们的分布。这里有一个 Mathematica 版本的代码的 github 地址，如果你想自己去探索它的话 (注意: 感谢 Stephen Wolfram 在一月份看了 Mathematica 代码并给我们提供了建议)

（实测地址是一个dropbox：https://www.dropbox.com/s/d2dfwhxdmzkp4y4/a-pattern-in-the-primes.nb?dl=0）

在有了这个最初的发现之后，Shaun开始在网上寻找其他以这种方式思考的人，这使他找到了我的文章，于是我们开始建立联系。

Shaun的算法揭示了质数分布所遵循的一个有趣模式，这个模式是非随机的，并且是分形的。据我们所知，质数与分形的结合尚属于前所未有的发现。

这种算法使我们能够轻松的观察到在任何一个数字区间——每个小区域表示一个数字区间，是否有质数存在。也能让我们很容易的观察到包含质数的区间与不包含质数的区间之间的分布情况。

当看到这种可视化的图像时，人们会让人想起符文、玛雅文字、挂毯和象形文字等等。如果你仔细观察一下，你会发现里面有不同层次的图形在循环嵌套，看起来有一种分形对称性，如下图：

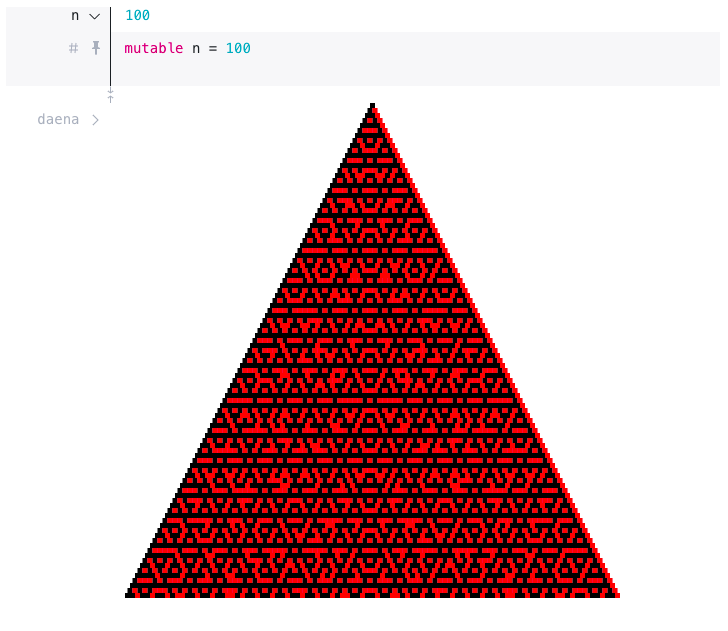
2.分形图像如何生成

上面的迷人图像是怎样生成的呢？其实并不复杂，接下来，让我们对上图进行逐行分析：

第一行：

由于1-6这六个数字中存在质数，所以标为黑色，那么图形的第一行就由一个黑色格子组成。

第二行：

由于第一列（左边）含有质数，右边不含有质数，所以左边区域标为黑色，右边则为红色。那么图形的第二行就由一个黑色格子和一个红色格子组成。

第三行：

同理，第一列、第二列都含有质数，所以对应黑色格子，第三列则对应红色格子：图形的第三行由黑色、黑色、红色三个格子组成。

以此类推，如果一个单元格所代表的数字序列中至少有一个质数，那么它就是黑色的，如果里面没有质数，则是红色。我们将逐行进行生成，组成了整个金字塔状的图案，令人着迷的是，有趣的几何结构在这种图案中涌现了出来。

3.图像与最大公约数序列

在上面的例子中，每个单元格代表了6个数字序列。而在上图中，每个单元格在正整数序列中代表100个数，即单元格宽度为100，并且保持了100行。单元格所代表的数字序列长度作为一个可调参数，我们称之为n，n是一个关键的变量，我们会在后文中多次见到他。

例如：如果 n=50，那么每个单元格代表50个整数，并且模式保持50行；如果 n=200，那么每个单元格代表200个整数，并且模式保持200行。

首先，我们发现上图中的模式（其中n为100）与已知的数字序列 OEIS A054521（即最大公约数序列）相匹配，并且在不同的尺度上它是自相似的。

注解：

所谓OEIS A054521（最大公约数序列）是一个金字塔形的数字序列，如下：

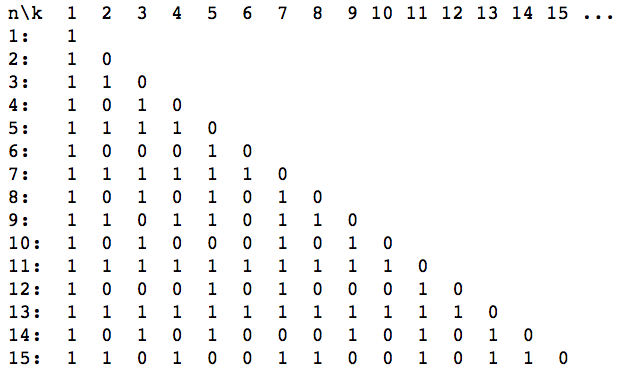
在这个金字塔形序列中，第i行的第 j 个位置表示 i 与 j 的最大公约数是否为1，如果他们之间的最大公约数为1，这个位置就填入1，否则填入0。

这个视频展示了随着 n 值增加，图像的整体变化。

然而，并不是所有的n值都能让图像与最大公约数序列相匹配。

例如，对于 n 取奇数，我们可以看到不同的模式，以下是 n=99 时的图像：

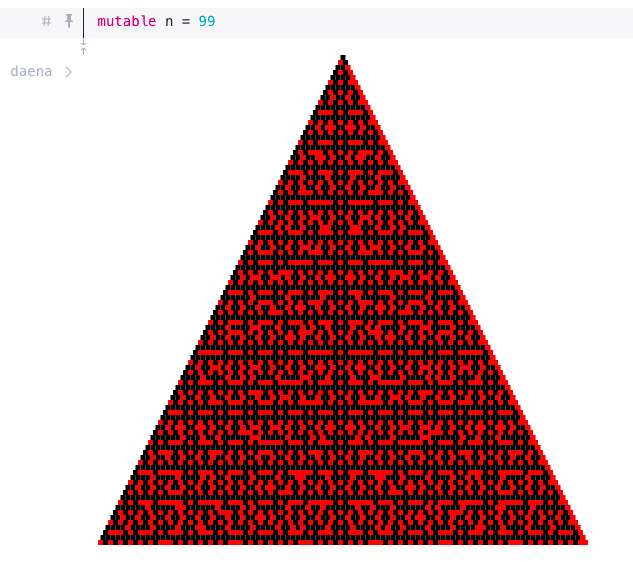
就像我们看到的 n 与最大公约数序列之间的关系一样，当 n 取奇数时，图形同样产生了分形结构，这意味着由质数按照这种模式产生的图形不仅可以与最大公约数序列产生巧妙的联系，而且一些我们尚未理解的变化形式也蕴含其中。

该算法还揭示了质数和非质数的序列排布规律，这些序列的排布可能对我们预测质数和非质数的区间有所帮助。

4.更进一步

在 Shaun 找到他的发现之后，我们花了很多时间，夜以继日地工作以观察这个新的可视化背后是否有更深层次的模式，最终我们取得了一些进展，找到了至少一个已知的序列，产生了 n 的偶数值模式。但是正如上面所说的，它不适用于所有的n 值，我们尚未在理论上进一步证明，也还没有测试过大量的 n 值并相互比较结果。

我们还不确定这一切到底意味着什么——这可能也并不意味着什么——它可能只是一次非常漂亮的可视化——但它足够有趣(至少对我们而言) ，我们最终决定公开这一切，以便其他人能够帮助我们进一步探索，谁能保证这件事不能更进一步呢？

也许这是一张关于质数分布的地形图？也许这在数论或者科学领域有用？在不同尺度上的自相似性、以及用一个已知序列并不能充分描述所有的 n 值的事实，意味着这里面可能还有更多的东西需要探索。

一般来说，在质数分布中发现任何类型的非随机模式都是很有趣的。这和其他的研究发现之间（比如我们最近在质数中发现的一个周期顺序的文章）又是否有联系呢？