质数分布、晶体衍射和分形几何——竟然被一个小实验联系到了一块儿

质数分布间隔的规律是什么?这是个至今仍未解决的问题。在本文介绍的研究中,晶体粒子以质数序列排布,在衍射实验中呈现出类似分形的结构,这为揭开质数之谜提带来来新的灵感。
1.质数序列的晶体衍射
当晶体学家将质数当作一个粒子系统,由此产生的衍射图样为现有的数论猜想创造了一个新的视角。
大约一年前,理论化学家Salvatore Torquato与即将从普林斯顿大学毕业的研究生、数论学家Matthew de Courcy-Ireland会面,介绍他关于质数的研究。质数,也就是那些只能被1和自己整除的正整数。
作为普林斯顿大学的化学教授,Torquato 的研究领域是物理系统结构中的模式(pattern),例如晶体、胶体中的粒子排布规律。他的一项重要成果是,做了大量用扁球状糖果填充瓶子的模拟实验,证明了球体不能最大化地填满密闭空间。在他的领域,常常使用X射线衍射来推断物质结构。
当X射线照射液体或玻璃时,无序的分子会将X射线散射到各个方向,不会形成明显的衍射图样。但是当X射线照射晶体时,晶体中有序排列的原子会同步地反射光波,波峰在某些位置叠加,发生相长干涉,产生周期性的亮斑。这些亮斑所在的位置被称为 “布拉格尖峰” 。这个名字是为了纪念晶体学家布拉格父子。他们早在1910年代就深入研究衍射现象,以揭示散射物体的组织结构。
将质数建模为一维粒子序列,实质是可以散射光的小球体。
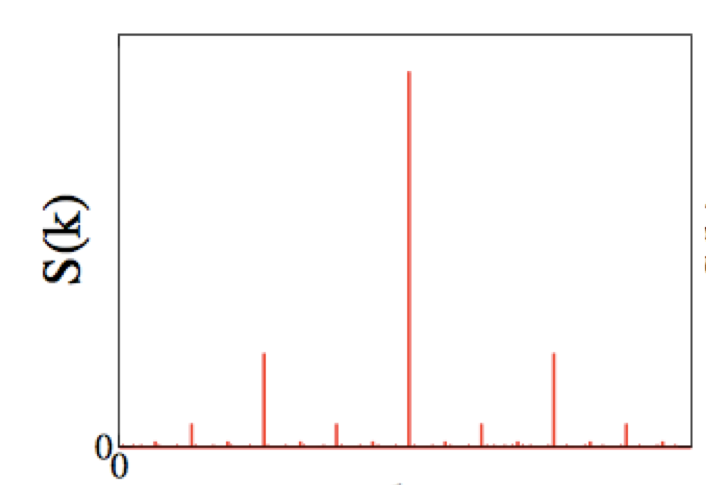
质数序列衍射实验出现了分形特征
在计算机实验中,他们用一百亿左右的,比如从10,000,000,019开始的质数序列做光学衍射。(他们发现这是一个“黄金区间”,在此区间内的质数数量足够多,对应的粒子密度足够大,产生的信号足够强,可以得到明显的衍射图样。)
Torquato 做实验时并不清楚会出现什么样的衍射图样,或者是否会有衍射图样。质数,所有自然数不可分割的组成部分,无规律地掠过数轴,像打水漂时石子掠过水面跳跃,激荡起深刻的问题。
de Courcy-Ireland表示, 在很多方面,质数与随机数字的序列都很难区分。虽然在过去的几个世纪里,数学家们已经发现了许多关于质数分布的规律,但仍然很难找到任何清晰的模式,所以我们只好把质数的分布看作是随机的。

从左到右:Salvatore Torquato,Ge Zhang and Matthew de Courcy-Ireland 写作了将质数序列看作产生衍射图样的粒子的新论文。
但是在一篇由Torquato,Zhang和计算化学家Fausto Martelli发表于2月份的《Journal of Physics A》杂志上,以及另外两篇de Courcy-Ireland参与但尚未进行同行评议的新论文中,科研人员发现,质数序列,并不像液体那样无序,而更像晶体,会产生衍射图案。
微软新英格兰研究院和麻省理工学院的数学家Henry Cohn表示,“这项研究的美妙之处在于,让我们(数学工作者)了解到晶体学家对质数的看法。”
Torquato 说,该研究产生的衍射图样与之前所见的任何衍射图样都不太一样,这意味着以质数序列排布的物理系统(晶体),是一类全新的结构 。普林斯顿的研究人员称这种类似分形的图样为 “effective limit-periodicity”(显著的极限周期性)。
质数通常可以用筛分的方法获得,例如对于100以内的正整数,依次过滤掉2, 3, 5, 7这四个质数的倍数。因此,在数轴上,除了2以外的所有质数都在奇数位置上,它们的间隔为2, 4, 6等2的倍数,且越往后,质数序列的间隔越大。衍射图样包含一系列周期性排列的明亮波峰,反映2这一最普遍的质数间距。其中最明亮的峰对应数轴上间隔为6的质数,以固定的间隔穿插在不那么明亮的峰之间。这些更暗的峰对应间隔更远的质数,如此层层嵌套,形成无限稠密的布拉格尖峰。
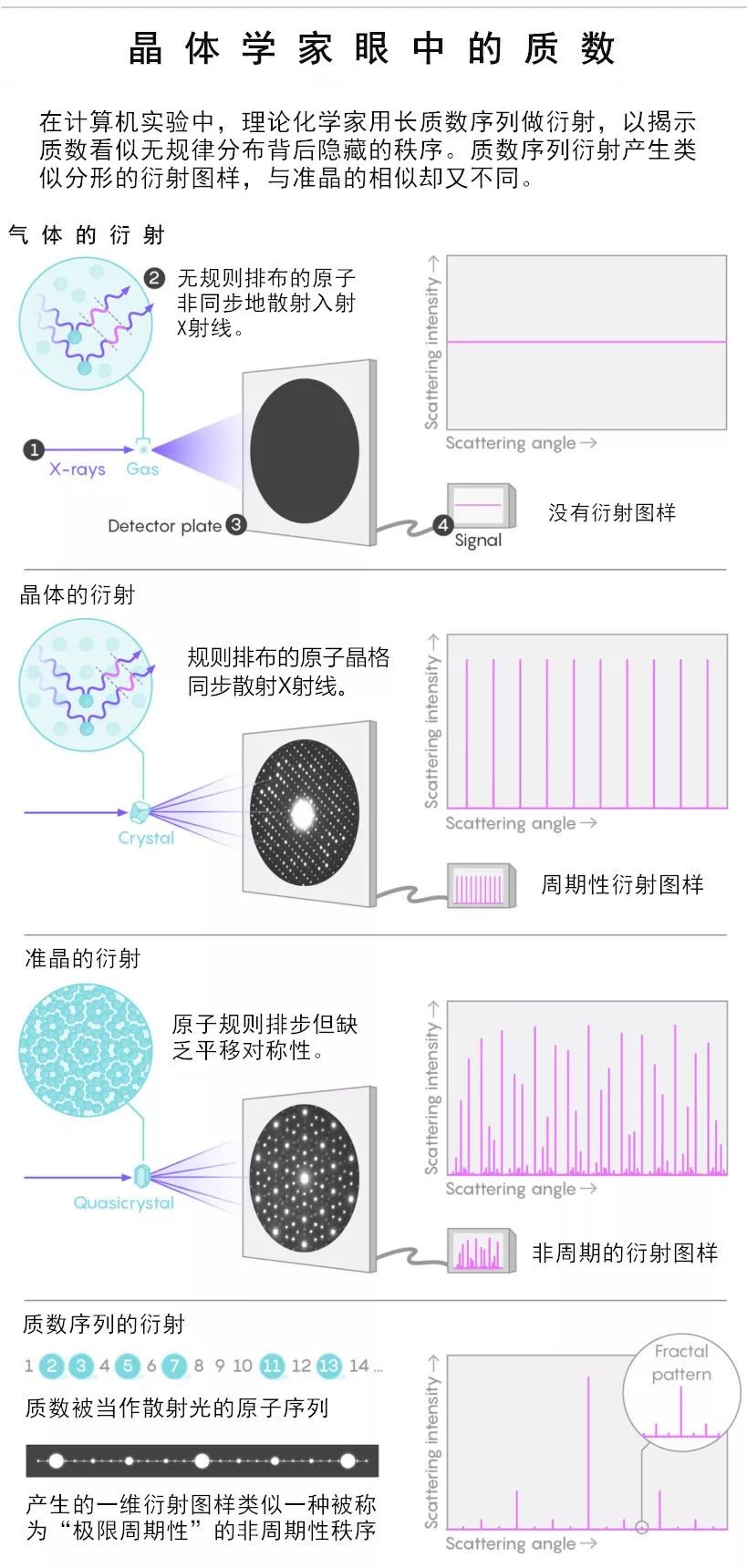
如此高密度的“布拉格尖峰”,人们曾经在“准晶体”衍射实验中看到过。准晶体是20世纪80年代被发现的一种介于晶体和非晶体之间的材料,它的原子排列具有一定的旋转对称性,却没有平移对称性。但是以质数间隔排列的粒子结构产生的衍射图像,峰与峰之间是一种分形结构。Torquato 认为,以质数间隔排列粒子,就像准晶,其实是一种全新的物质状态,但它的性质又和准晶体不同。
许多接受采访的数论学家都表示,这个研究团队的发现还不足以引发数理领域的进步。这项研究涉及的数学,几乎上都不是新的。事实上,当Torquato去年春天向de Courcy-Ireland展示他的计划和公式的时候,这位年轻的数学家很快就看到,质数衍射图样实验可以被现有的数论猜想所解释。
一年前,这两人在新泽西州普林斯顿大学高等研究院第一次会面,Torquato当时在那里休假。作为化学家的Torquato告诉作为数学家的de Courcy-Ireland,他可以使用公式来预测“孪生质数”的频率(孪生质数是一对间隔为2的质数,如3和5,17和19)。de Courcy-Ireland 认为Torquato的方法实际上也可以预测所有其他间隔的质数对。
布拉格尖峰的公式在数学上等价于Hardy-Littlewood 的质数k元组猜想,这是英国数学家哈代(Godfrey Hardy)和李特尔伍德(John Littlewood)在1923年发表的猜想:质数元组是存在的。这个猜想为具有固定间隔的质数组的出现频率做出了精确估计。
如前所述,质数通过依次筛分掉2, 3, 5, 7等质数的倍数获得。因此,质数首先是间隔为2的奇数,相应地,“孪生素数”为最小也最普遍的质数组。而由3个连续奇数组成的质数组只有{3,5,7},在此之后任意三个连续的奇数中,始终会有一个数可被3整除,如{7,9,11}。
Hardy-Littlewood猜想进一步明确了所有可能的质数元组在数轴上出现的频率。即使是最简单的 Hardy-Littlewood情形——“孪生质数猜想”,在经历了现代科学爆发式的进步之后,仍然未被证明。专家们认为质数衍射实质上只是重新阐释了Hardy-Littlewood猜想,所以它不能证明Hardy-Littlewood猜想,或者说不能证明黎曼猜想。黎曼猜想于1859年提出,将质数分布问题与黎曼Zeta函数的零点问题联系在一起。
2.质数与非周期性序列
非周期性序列(aperiodic order)”准晶
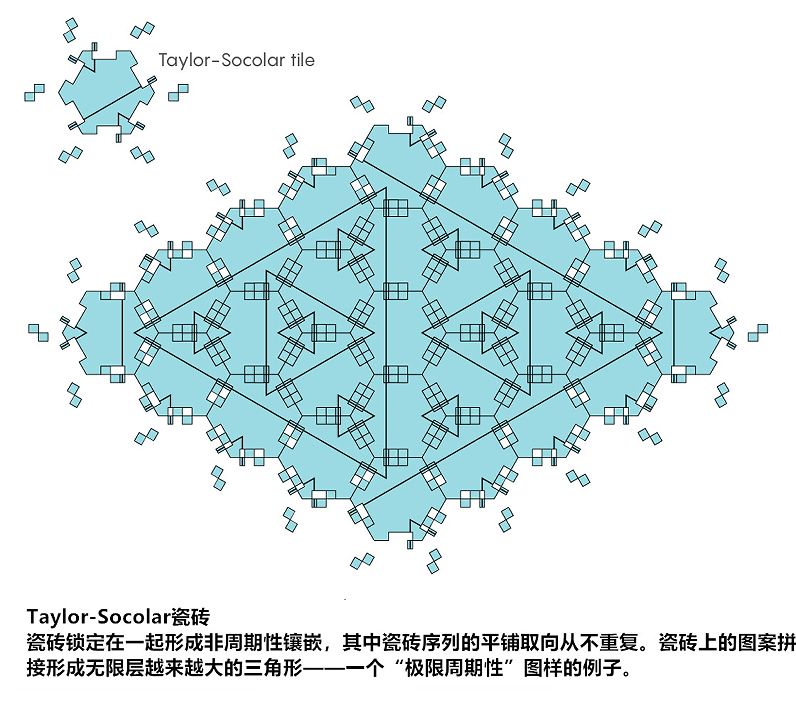
非周期性序列极限周期性
2010年,杜克大学的 Joshua Socolar对其进行细节分析。计算机实验的研究表明,物质的极限周期性应该能够在自然界中形成,计算也表明这种系统可能具有不寻常的特性,当时没有人将它与质数联系在一起。在Taylor-Socolar镶嵌瓷砖系统中,质数间隔的同步性仅仅是统计意义上的,显著的极限周期性是一种全新秩序。
1976年,哥伦比亚大学的
布里斯托大学的Jonathan Keating认为,质数衍射图样的主要优点在于,它引发不同思维方式的连接。对此,蒙特利尔大学的数论学家Andrew Granville则认为,Torquato及其团队的研究不过是自命不凡,仅仅是已有想法的重复罢了。
Torquato不特别关心数论学家如何评价他的研究,他找到了窥探质数规律的方法,“事实上,我认为这项研究非常惊艳,直击人心。”
推荐阅读
Love is all you need | 无标度网络理论之父回应质疑

集智QQ群|292641157
商务合作|zhangqian@swarma.org
投稿转载|wangting@swarma.org
◆ ◆ ◆
搜索公众号:集智俱乐部
加入“没有围墙的研究所”

让苹果砸得更猛烈些吧!
始发于微信公众号: 集智俱乐部










