导语

物理学理论往往精妙简介，蕴含着对自然的深刻洞察，但是否只有物理学家才总结出物理规律呢？最近有研究者受到机器翻译的启发，用量子力学实验结果来训练人工神经网络，发现机器竟然也可以学到量子力学的知识。

原题：Rediscover Quantum Mechanics in Machine Learning

涌现无处不在

涌现（emergent）现象是凝聚态物理学中的一个重要研究课题。涌现现象不仅存在于物质和相互作用力中，也存在于时空和重力场中，物理学的前沿领域正在研究这些新奇的思想。

等会儿！你有没有发现——

这些物理理论本身也是一个涌现现象？

这确实是一个有趣的思考角度。物理理论确实是人类大脑中神经活动的产物。我们确实搞不清楚，在物理学家大脑里的神经网络中，这些物理理论是如何产生的？或者更加宽泛的来说，在物理学界中，探究复杂网络中涌现出智能的原因也是科学研究的目标之一。

在理解智力这个问题上，我们只是刚刚起步。不过随着近些年机器学习的兴起，却使得我们在这个问题上又前进了一步。人工神经网络领域的进展，可否用来帮助我们从实验数据中去探究物理概念和物理规律？

以量子力学为例，假设人们尚未发现描述量子力学的方程式，但科学家仍然能在一定程度上知道如何进行冷原子（cold atom）实验来收集不同形状势阱中的玻色-爱因斯坦凝聚态（Bose-Einstein condensate BEC）的密度分布。

既然如此，那么量子力学是否是一种基于实验的最理性最自然的理论，而没有受到人类文明已有偏见的影响？或者说，人工智能、机器学习是否能够“学习”到另外一种形式的量子力学？

序列模型自学量子力学

论文题目：

Uncover the Black Box of Machine Learning Applied to Quantum Problem by an Introspective Learning Architecture

论文地址：

https://arxiv.org/abs/1901.11103

在我们近期的一项研究中，让机器去预测 BEC 的密度分布。通过这项任务，我们让机器学会了量子力学。机器学习的模型只能获得电子势能（potential）和电子密度（density）的数据，而波函数（wave function）以权重参数的形式隐藏在神经网络当中。

之所以这么做是受到了机器翻译的启发。

机器翻译就是将输入的一种语言转化为另外一种语言，而其中的语义则隐含在了机器学习的模型中，这样的机器学习模型可以包含所有语言通用的词语的含义。通过分析语义模型的空间结构，我们能够获取翻译器所学习到的词语之间的关系。

为了把机器翻译这个模型应用在量子物理的研究中，我们把电子势能-电子密度分别视为两个序列，这样就可以采用机器翻译中所常见的神经网络模型（循环神经网络 RNN）进行处理。

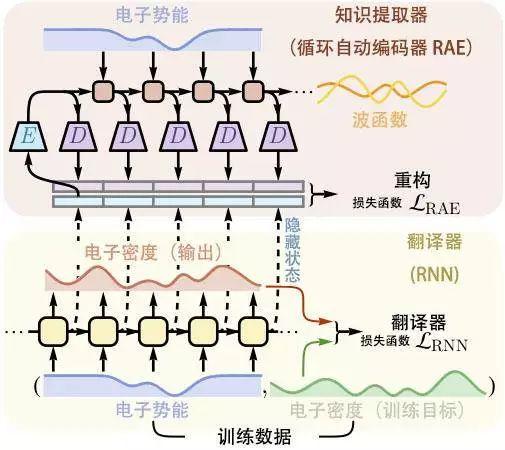
研究者使用的训练学习模型架构：薛定谔机器（the Schrödinger machine）

我们训练一个循环神经网络，沿着一维势阱（one-dimensional trap）输入电子势能数据，使之能够输出对应的电子密度数据。在学会这种转换的过程中，机器也一定能获得了关于量子物理学的基本直觉。为了获取神经网络在学习过程中所获得的知识，我们设计了另外一个高层次的机器称作知识提取器，用这个知识提取器去提取神经网络隐藏层中的知识。

知识提取器本质上就是一个循环自动编码器（RAE），它的作用就是尽可能的压缩循环神经网络内部的节点状态，同时又不失去其输出结果的稳定性。就像自动编码器能够筛选出输入样本的主要特征一样，知识提取器可以提取重构出那些至关重要的本质变量。

研究表明，当知识提取器的空间维度降到两维以下时，所能重构的知识数量就会大打折扣。这意味着科学家至少需要两个变量去描述电子势能-电子密度的转换方程。

当我们把这个二维图像画出来的时候，会发现它们其实对应着波函数的实部和虚部。当我们把已经发现的规则更新回神经网络后，发现它们确实互相影响，这个关系能精准的匹配薛定谔方程的离散形式——神经网络中确实蕴含了量子力学的知识。

此外如果我们放宽对知识提取器的约束，神经网络也能够得到其它的量子力学知识，比如说密度泛函理论，只不过这需要三维空间，即三个实变量。不过就这两个“神经网络版”的波函数和薛定谔方程而言，我们人类所发现的对量子力学的描述确实是最为经典的版本，这一点倒是令人类科学家感到一丝欣慰。