在许多简单的疾病传播模型中,都假设了具有统一的基本传染数(R0)的同质性人群。每个感染者平均会引起R0个新感染者,R0>1则疾病会持续传播,R0<1则传播逐渐停止。新冠疫情以来,对于新冠病毒R0值的估计大多在2-3之间。
真实情况下,人群的异质性、社会网络结构差异、不同的管控措施、病毒的变异等,都会引起R0波动,进而影响数据分析和判断。目前已经有一些基于主体或网络的模型,开始考虑到复杂参数的影响。
Christopher Wolfram 近日在Complex Systems期刊在线发布论文,构建基于主体的COVID-19模型(An Agent-Based Model of COVID-19),研究了多主体模型在不同场景、不同参数下的具体行为变化。
Christopher Wolfram(左)和Steven Wolfram(右)
存在临界点:随着主体之间互动率(interaction rate)的变化,存在一个鲁棒的临界点。它决定了最终是大部分人被感染,还是小部分人被感染。(即在临界条件下,R0≈1。)
接触网络的结构显著影响着疾病传播。在B-A网络上的传播速度非常快。W-S网络传播速度处于中间水平,而由W-S团簇组成的超图结构传播最慢。
降低社团之间的互动会增加结果的不确定性,但会压平增长曲线,降低平均总感染率。
互动率的异质性显著影响着疾病传播。即建模不应只考虑平均的互动率,而要考虑主体之间互动率的分布。
论文题目:
An Agent-Based Model of COVID-19
论文地址:
https://www.complex-systems.com/abstracts/v29_i01_a05/
作者公布了论文的PDF版本。扫描下方二维码即可在线浏览或下载:
作者首先构建通用模型,并分析了相图,然后探索了可能的参数空间。
论文以图的形式表示人群中的联系网络。每个节点表示一个主体(agent),每条连边连接两个可能互动的agent。每个主体被标记为易感染、被感染或痊愈三种状态。
在实验中,每个时间步,主体都会在联系人网络中随机选择其邻居,并与之会面(即互动)。会面是相互的,哪个主体发起并不重要。最后,被感染的主体会在一段时间后恢复。持续上述步骤直到被感染的主体完全消失。
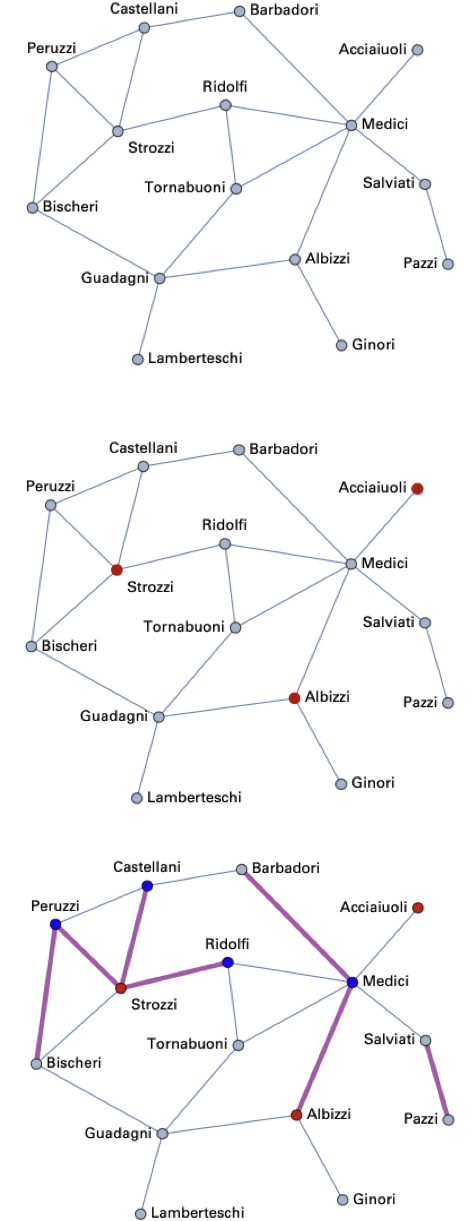
图1-图3:以Florentine家族为例构建社交网络,将其中被感染的主体(agent)标红。在模拟开始时,少量随机主体被感染。之后新感染者被标记为蓝色,感染路径标记为紫色。
图4:从Watts-Strogatz图分布采样、具有1000个节点和10%重连概率的随机图。
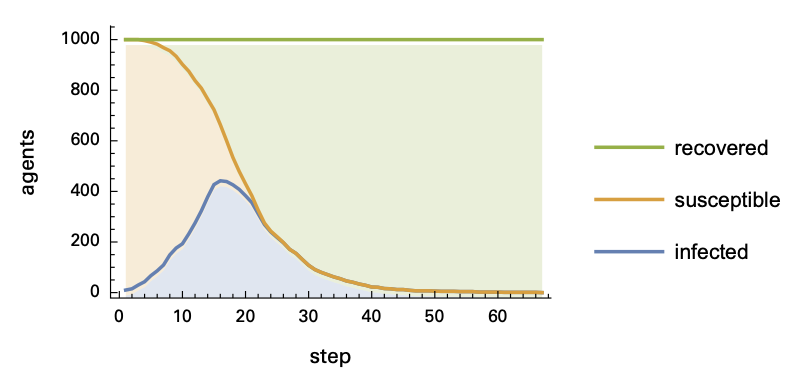
图5:随着时间步推移,易感染(橙色)、被感染(蓝色)和痊愈(绿色)的主体数量变化。
此时该模型是典型的SIR模型(Susceptible,Infected,Recovered)。
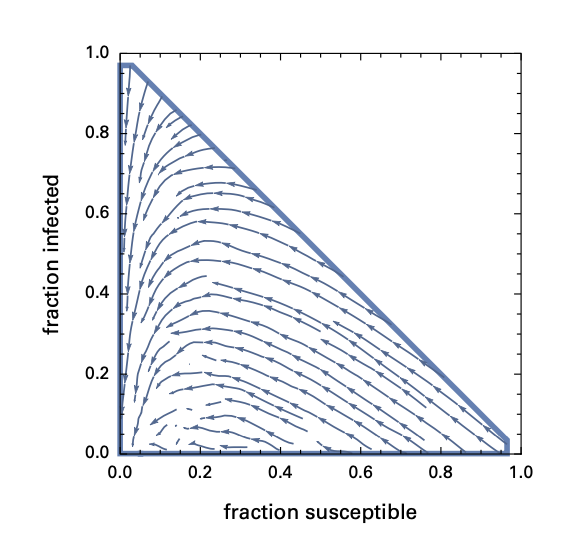
对上述模拟的演变过程可视化,可以让曲线穿过一个易感染、被感染、痊愈分别是坐标轴的三维空间。但由于易感染主体+被感染主体+痊愈主体=主体总量,因此可以只用二维平面来表示传染病演化曲线。
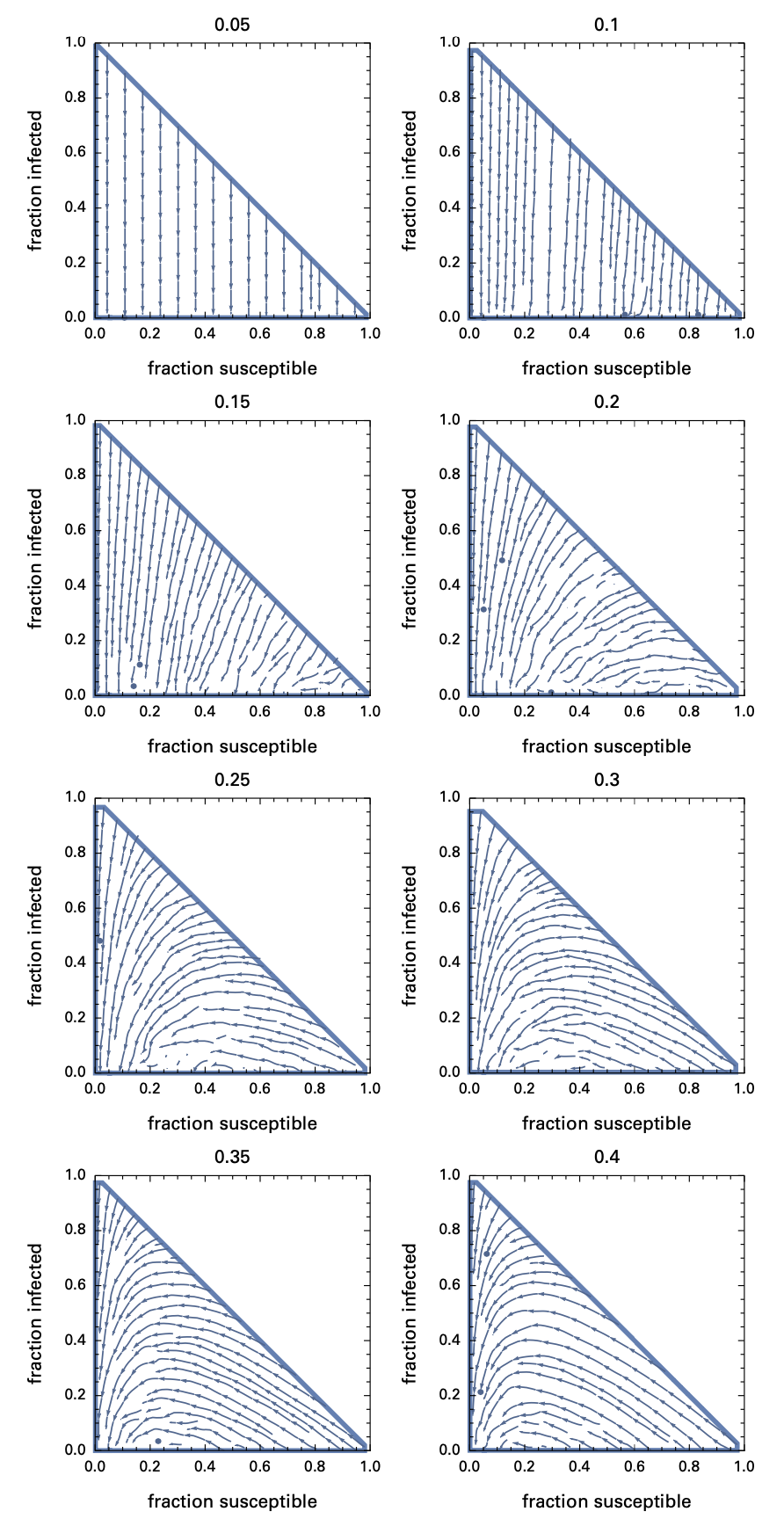
图7:考虑到痊愈时间的几何分布,再将相位图拓展到向量场中,从而寻找临界点和吸引子。
显然在{0, 0}位置有吸引子。在此参数下(infected–>0,susceptible–>0)所有人都被感染。后文则研究不同参数会对相图有怎样的影响。
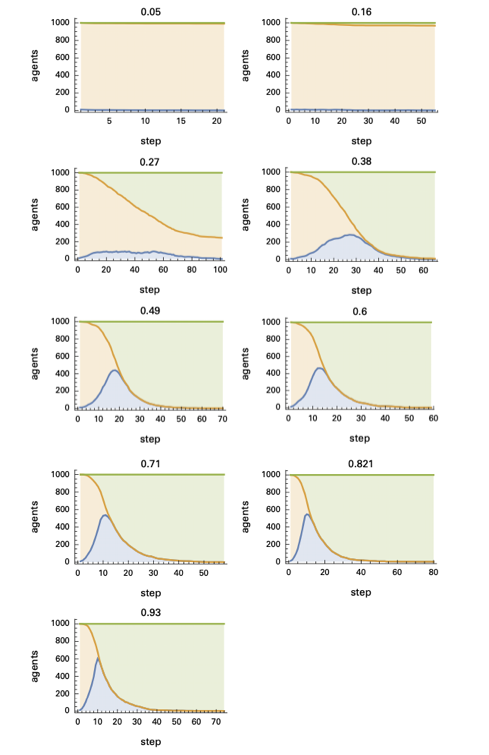
图8:随着时间推移,易感染主体(橙色)、被感染主体(蓝色)和痊愈主体(绿色)的数量,因为每个时间步主体的会面次数不同而不同。
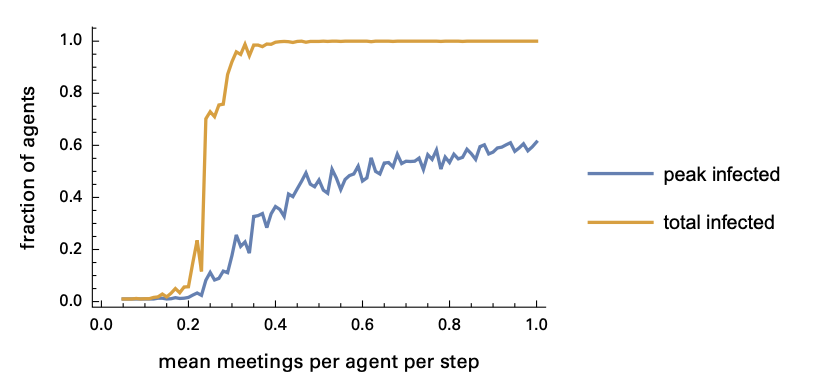
图9:感染率峰值和总感染率随平均会面次数变化的函数
随着会面次数增加,曲线会越过一个临界点——一旦越过,就注定几乎所有人都会感染。绘制单次增长峰值和总感染率曲线,明显可以看到临界点的存在。在每个时间步下,当主体的平均会面次数超过0.2,总感染率会快速上升到接近100%。
当互动受限时,在相图底部边缘有吸引子(无人被感染),随着会面的增加,该吸引子被快速推到了左下角(无人被感染或者易感染)。

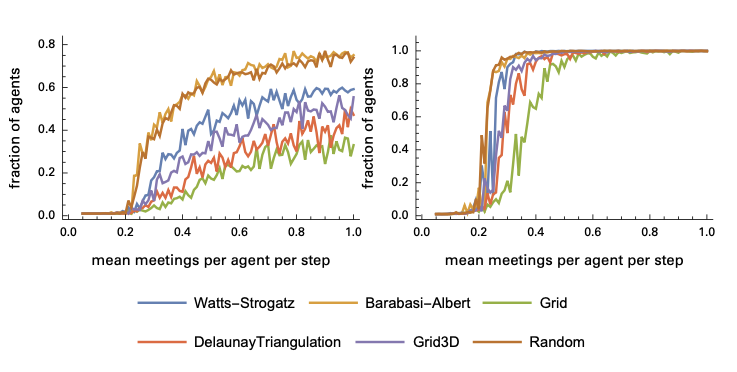
图11:研究者在上述不同网络上进行仿真实验,以确定网络结构对传播的影响
图12:感染率峰值(左)和总感染率(右)随着平均会面率变化的函数。虽然不同网络结构上的临界点接近(0.2),但高互动率(会面率)的感染情况却差异很大。
其中B-A无标度网络的疾病扩散速率高于W-S小世界网络。
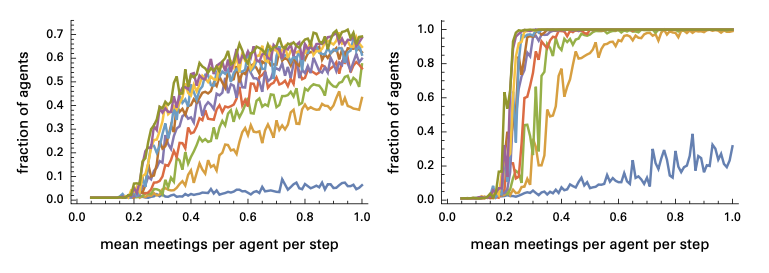
图13:感染率峰值(左)和总感染率(右)随着平均会面率变化的函数。不同颜色的曲线代表在不同密度W-S网络上的测试结果。稀疏的网络(下方蓝线)疾病扩散很慢,较密集的网络则迅速扩散。进一步说明网络结构的重要性。
社交网络通常被认为是小世界的,但通过人与人见面(传播疾病)形成的联系网络,却未被证实也是小世界的。因此作者构建了由多个小团簇组成的超图。每个团簇内部是一个小世界网络(如城市城镇等地理实体),团簇之间是表示这些地理实体连通性的平面图(planar graph)。通过调整临近团簇之间的连边数量、团簇内部的连通性,最后发现,减少社团之间的互动可能比减少社团内部的互动更有效。
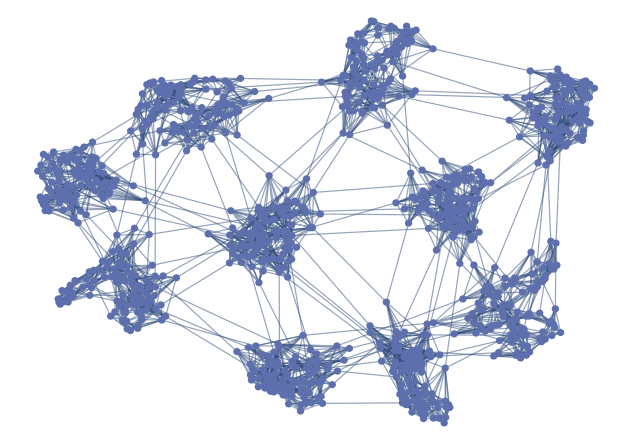
图14:一个具有10个社团的超图(supergraph)示意图,每个社团包括100个顶点,并且有5条连接着相邻社团的边
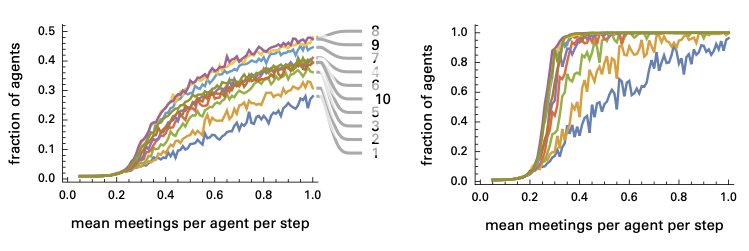
图15:感染率峰值(左)和总感染率(右)随着平均会面率变化的函数。团簇间的连接数从1到10,分别模拟,以不同颜色的曲线表示。
将最初感染的agent强制放在一个团簇中,向其他团簇扩散。当团簇之间的连接变弱时,疾病传播的速度不出所料地降低了。而且感染率是随着会面率缓慢增长的。其原因是,尽管在社团内部(小世界团簇)迅速传播,但在大尺度的平面图上却没有那么快递传播。
随着团簇之间的联系越来越紧密,曲线开始接近在大的小世界网络(所有主体都在其中)上模拟的形状。但当团簇处于弱连接状态时,曲线却截然不同。
这意味着减少社团之间的互动(团簇间连接数),比减少社团内部的互动(平均会面率)更有效。
集智斑图顶刊论文速递栏目上线以来,持续收录来自Nature、Science等顶刊的最新论文,追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能,每周通过微信服务号「集智斑图」推送论文信息。扫描上方二维码即可一键订阅。
👇点击“阅读原文”,在线浏览或下载论文PDF文件