系统的复杂度,虽然有很多定义方式,但作为复杂性科学的基本问题,远远没有获得确定的回答。重整化群可以通过数学变化,统一地考察不同尺度的物理系统。近日发表在PNAS的一篇论文,基于重整化群,提出了在多层级复杂系统中定量描述复杂度的新方法。
论文题目:
Multiscale structural complexity of natural patterns
论文地址:
https://www.pnas.org/content/117/48/30241
最广为人知的定义复杂度的方式,称为Kolmogorov复杂度,该方法使用能够对某一信息编码的程序的最小长度,来代表一段信息的复杂度。例如101010相比110001,前者由于存在规律,能够用更短的程序描述,其复杂度更低。
如果不同尺度的子系统间相似度较低,那么系统的复杂性也越高。然而,我们对复杂度的直觉,告诉我们需要该定义同时反映系统中有多少组件及连接,以及系统中的这些组件及连接是否可见。基于系统自相似来定义复杂度的方式,只反映了后者,没有考虑那些系统中隐藏的连接,不完全符合我们对复杂度的直观映像。
在真实环境,例如生物系统、社会系统中,往往同时存在多个层级,不同层级的结构,以及受到的约束存在显著区别。考虑到复杂系统往往是层级化的,对系统复杂度的定义就必须考虑到不同层级,而不能主观地规定某一层级的特征是本质的。复杂科学需要提出一个明确定义,能够整合不同层级信息、且具有鲁棒性的复杂度定义。对于那些完全有序或完全无序的系统,该定义得出的复杂度都应该极低。
这篇PNAS论文,提出了基于重整化群的复杂度定义方法。
例如拍照的时候zoom in,发现看到的现象有些接近,将小尺度的现象,放到大尺度去分析。由于系统具有自相似性,通过对比两种模式下分析的差异,可以用大尺度的分析,来作为对小尺度现象的建模。这可以看成是重整化群的通俗理解。
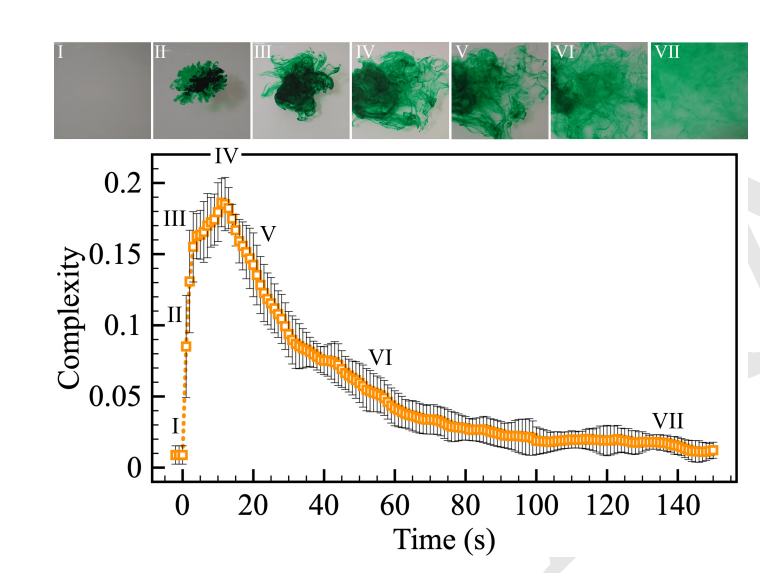
如何计算上面这幅图片的复杂度?重整化群的方法,是将该图分为16份,再将图中的某一份放大之后分为16份,将其中像素平均后,得出该子图的不同区域像素值。将原图的16个子图依次排列,得到A,再将子图分割排列得出图B,计算图A和图B之间的差异,得出图O。将所有如此分割得出的图O的复杂度加和,就完成了一个层级上的迭代,将不同层级的结果加和,即得出了原图的复杂度。
上图中从左到右,该方法计算出的复杂度依次升高,这展示了使用该方法,可以衡量图像的复杂度,符合人类直觉。具体对的计算方法和公式,请参考原文。
在统计物理中,Ising 模型描述了磁性原子之间由于相互作用,而形成的晶格。由于该模型中,参数在某个阈值左右的细微变化,就能引起系统整体的显著变化,这被称为相变。发生相变前后,系统的复杂度会发生显著变化,这可以用来验证新提出的复杂性度量方法。
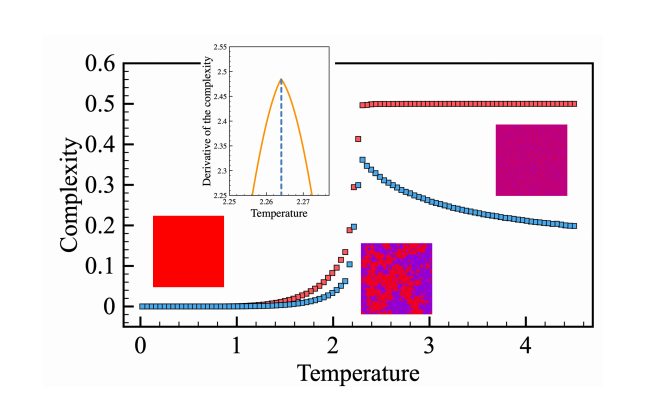
图3. 二维Ising模型的模拟数据下,不同温度和复杂度的对应关系
上图中,横轴温度可以看成是系统具有的能量,能量越高,系统越无序。红色和蓝色的线代表计算复杂度时,迭代计算的次数不同,即对复杂度的计算方法有所不同。不论那种计算方法,当相变发生时,复杂度都会呈现显著变化。而蓝线对应的算法,当系统的无序程度进一步提升时,复杂度下降,这符合一个完全无序的系统没有处在混沌边缘系统复杂的直觉。而红线对应的算法,由于迭代次数过少,导致其不会考虑更小尺度的差异,相变点之后,复杂度就不再变化。
而在更高维度,以及真实的微粒扩散过程中,该方法都能够反映出相变现象。如下图所示
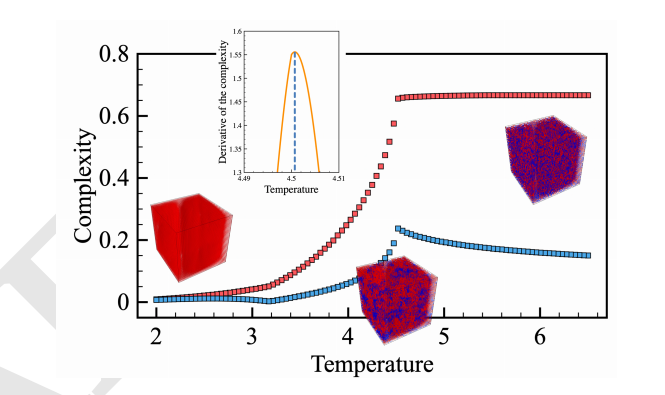
图4. 三维系统中,基于重整化群的复杂度算法得出的复杂度和系统温度的关系
以上实验说明,在固态物理中,可以使用该方法,根据实验得出的图像来发现如法通过实验找到的相变现象。
此外,在机器学习中,系统的复杂度可以成为额外的信息来源,例如在应对对抗性攻击,即通过改变少数像素点,就改变对应分类标签。例如本文作者假设上述改变会增加图片局部的复杂度,从而改变原图中各个子图的复杂度分布,据此识别对抗性的训练数据集。
而在生物领域,复杂度这一概念的应用虽然鲜有研究,但通过计算处在进化树上不同物种的基因序列的复杂度,可以研究进化过程中的相变点,即生物集中爆发或产生显著变化的过程。不同层级系统间的竞争和制约,被认为是生物体复杂性的来源之一。而这也反映了时间及空间层面上的不同系统存在的不相似性,在复杂性科学的核心位置。
测量复杂度还对因果发现有启发。之前的研究中,根据对不同信号压缩的难度差异,判断信号间的因果方向,更难压缩的信号是因[1]。据此我们可以推测,考虑不同系统间的复杂度随时间变化的曲线的先后,有可能可以判断出两个系统间的因果箭头。这有赖进一步的研究。
1. SY, Pranay, and Nithin Nagaraj. “Causal Discovery using Compression-Complexity Measures.” arXiv preprint arXiv:2010.09336 (2020)
集智斑图顶刊论文速递栏目上线以来,持续收录来自Nature、Science等顶刊的最新论文,追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能,每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅: