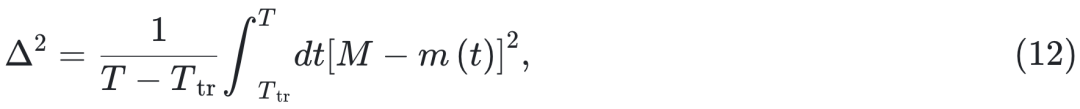许多现实世界的复杂系统通过稀疏异质网络相互作用,而传统动力学平均场理论在处理这类系统时存在一定局限性。这篇工作首次将动力学平均场理论扩展至稀疏有向网络,推导出单自由度有效动力学的路径概率精确方程并开发高效求解算法。这一理论突破弥合了网络结构与系统动力学研究间的鸿沟,并且该框架广泛适用于神经网络、生态系统和流行病传播等多种复杂系统,为理解稀疏异质网络上的集体动力学行为提供了严格数学基础。
研究领域:稀疏有向网络,动力学平均场理论,路径概率,神经网络模型,相变,混沌动力学,群体动力学算法
论文题目:Dynamical Mean-Field Theory of Complex Systems on Sparse Directed Networks
论文地址https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.134.037401
尽管现实世界中的复杂系统通常通过稀疏且异质的网络进行交互,但其动力学的解析解仅限于全连接相互作用的模型。在此,我们在具有随机结构的稀疏有向网络上,解决了广泛非线性复杂系统模型的动力学问题。通过将动力学平均场理论 (dynamical mean-field theory,DMFT) 推广到稀疏系统,我们推导出了描述单自由度有效动力学的路径概率的精确方程。方程通用解适用于神经网络、生态系统、流行病传播和同步研究中的关键模型。利用群体动力学算法,我们求解了路径概率方程,以确定稀疏状态下开创性神经网络模型的相图,表明该模型随着网络拓扑结构的变化从不动点相转变为混沌相。
复杂动力系统由 N 个自由度 xi(t) (i = 1,…,N) 建模,这些自由度根据微分方程随时间演化
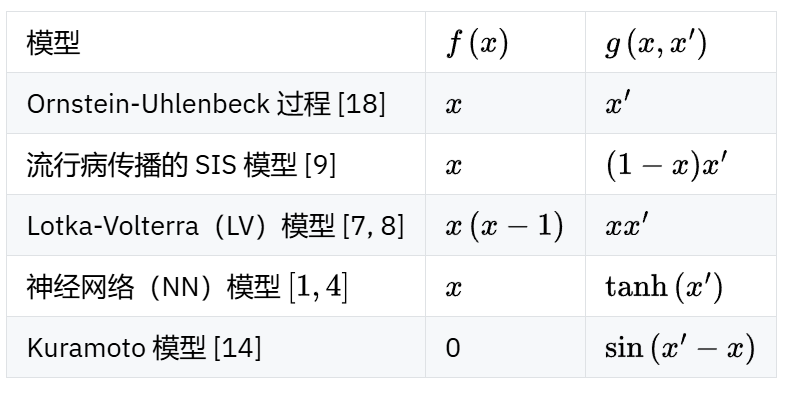
其中 {Aij}i,j = 1,… ,N 定义了交互网络。函数 f(x) 控制无相互作用时的动力学,核函数 g(x, x’) 则决定了成对耦合。方程 (1) 可用于模拟神经网络 [1 – 5] 和生态系统 [6-8] 、流行病传播 [9-12]、同步现象 [13-15]、观点动力学[16-17]以及多元 Onstein-Uhlenbeck 过程 [18 – 20] 的非平衡动力学。表 I 给出了复杂行为典型模型的 f(x) 和 g(x, x’) 的具体形式。
表 I. 由方程 (1) 建模的复杂系统中 f(x) 和 g(x, x’) 的显式形式。SIS 模型的方程 (1) 是通过淬火平均场近似[12,21,22]推导得出的。
复杂系统研究中的首要问题是如何将大量相互作用元素的动力学简化为少数变量的动力学 [23]。动力学平均场理论 (DMFT) [24-26] 是在极限N→∞下解决这一问题的有力方法,它能根据单自由度有效动力学的路径概率给出一个解。将 DMFT 应用于方程 (1) 所描述的模型已经引起了极大的关注[2-5,7,8,15,19,20,27-34],特别是在神经网络和生态系统的背景下。这些模型的相图揭示了丰富的现象学特征,包括不同类型的相变[5,7,30]、混沌行为 [1,3]以及多个吸引子的共存[7,8,35]。尽管在理论上取得了重大进展,但目前 DMFT 仅局限于稠密网络,其中每个动力学变量本质上都通过高斯相互作用强度与所有其他变量耦合。然而,现实世界复杂系统中的相互作用多数是稀疏且异质的 [36,37]。稀疏性表明系统中的每个元素平均只与有限数量的其他元素相互作用,而异质性则指相互作用网络局部拓扑结构的波动。如何将这些更现实的特征纳入由方程 (1) 建模的系统的 DMFT 形式体系中仍然是一个未解决的挑战,甚至像推导稀疏复杂系统的相图这样的基本问题仍然难以解决。
另一方面,在伊辛自旋(Ising spins)系统的情况下,稀疏网络上复杂系统的动力学已经得到了广泛研究[38-50]。在这种情况下,空腔方法 [39] 和 DMFT [38, 40] 都能根据单个动力学变量的有效动力学的路径概率提供解析解。然而,双向边的存在会引发时间反馈,在稀疏系统的特定情况下,这会导致路径概率维度呈指数增长[38,40,49],使得数值计算不可行。通过近似方案,如单次近似 [39],使这些计算成为可能[42,43,48]。当相互作用是有向或单向时,由于不存在时间反馈,路径概率方程可以被高效地求解[38,39,51]。
受伊辛自旋系统研究结果的启发,在本文中,我们解决了由方程 (1) 支配的模型在具有异质拓扑结构的稀疏有向网络上的动力学问题。该解是复杂系统研究中的一个基础性步骤,因为它最终将复杂网络的稀疏和异质结构纳入了 DMFT 的形式体系中。有向网络之所以引人关注,是因为它们能够对现实世界复杂系统中的非互易相互作用进行建模 [52],包括人类大脑皮层 [53]、食物网 [37, 54, 55]、基因调控网络 [56, 57]、在线社交网络 [58, 59] 和万维网 [60]。因此,这里提出的形式体系为分析研究现实相互作用如何影响复杂系统的动力学提供了可能性。
通过将 DMFT 推广到稀疏系统,我们得到了一个描述 N→∞ 下单变量有效动力学的路径概率的精确方程,并利用群体动力学算法 [61-66] 求解了表 I 中不同模型的该方程。我们的理论结果与有限系统的数值模拟之间的良好一致性证实了我们的解适用于通过不同网络拓扑结构相互作用的各种非线性模型,包括具有幂律度分布的网络 [36]。
作为应用,我们确定了 Sompolinsky 等人 [1] 提出的神经网络模型在稀疏状态下的相图。我们表明,相图显示出平凡和非平凡的不动点相、平均活动为零的混沌相以及平均活动非零的混沌相 [30]。通过计算某些宏观可观测量,我们确定了神经网络模型的相变线作为平均度和耦合强度方差的函数,表明它们与从随机矩阵理论推导出来的普适临界线一致 [67 – 69]。特别地,我们提供了数值证据,表明混沌相之间的转变与相互作用矩阵的主特征值和次主特征值之间的间隙消失相吻合。
设 Aij= CijJij 为 N×N 相互作用矩阵 A 的元素。二元变量 Cij∈{0,1} 确定网络拓扑结构,而 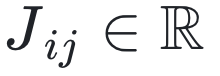 控制相互作用强度。如果 Cij = 1,则存在一条从节点 j 指向 i 的有向边 j→i,否则 Cij = 0。入度
控制相互作用强度。如果 Cij = 1,则存在一条从节点 j 指向 i 的有向边 j→i,否则 Cij = 0。入度 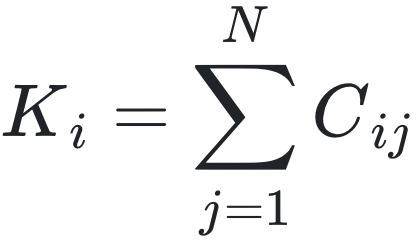 和出度
和出度 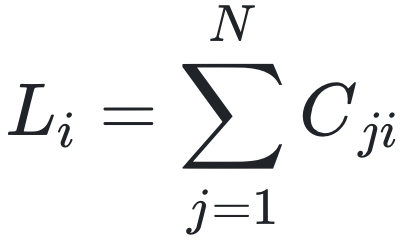 分别计算进入和离开节点 i 的链接数量 [36]。随机变量 {Cij}i≠j 遵循分布
其中
分别计算进入和离开节点 i 的链接数量 [36]。随机变量 {Cij}i≠j 遵循分布
其中 是归一化常数且 Cii = 0。度 {Ki, Li}i = 1,…,N 是从
是归一化常数且 Cii = 0。度 {Ki, Li}i = 1,…,N 是从  中抽取的独立同分布随机变量,其中 pin,k 和
中抽取的独立同分布随机变量,其中 pin,k 和  分别是入度和出度分布 [36,64]。参数 c 是平均度
方程 (2) 定义了一个网络集合,其中有向链接以概率 c/N 随机放置在节点对之间,服从
分别是入度和出度分布 [36,64]。参数 c 是平均度
方程 (2) 定义了一个网络集合,其中有向链接以概率 c/N 随机放置在节点对之间,服从 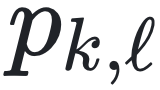 生成的预设度序列。在 N→∞ 的极限情况下,从方程 (2) 生成的网络样本与由配置模型[70,71]生成的样本相似。耦合强度 {Jij}i,j = 1,… ,N 是从均值为 μJ 、方差为
生成的预设度序列。在 N→∞ 的极限情况下,从方程 (2) 生成的网络样本与由配置模型[70,71]生成的样本相似。耦合强度 {Jij}i,j = 1,… ,N 是从均值为 μJ 、方差为 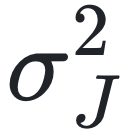 的分布 pJ 中抽取的独立同分布随机变量。分布
的分布 pJ 中抽取的独立同分布随机变量。分布 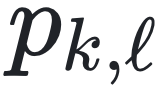 和 pJ 完全确定了网络集合,从而可以系统地研究网络异质性如何影响复杂系统的动力学。
和 pJ 完全确定了网络集合,从而可以系统地研究网络异质性如何影响复杂系统的动力学。
我们使用动力学平均场理论 (DMFT) [24 – 26] 求解方程 (1) 在有向网络上的耦合动力学。我们考虑稀疏状态,其中平均度 c 是有限的,与 N 无关。动力学平均场理论基于生成泛函
在固定时间区间内观察到状态变量的动力学路径 x(t) = (x1(t) ,…,xN(t) 的概率密度  。{xi(t)}i = 1,… ,N的相关函数可由
。{xi(t)}i = 1,… ,N的相关函数可由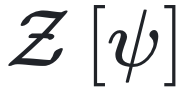 关于外部源
关于外部源 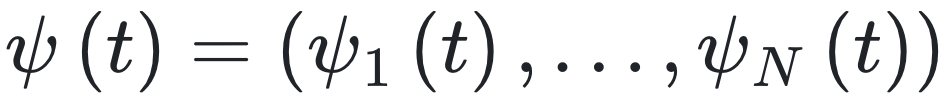 的导数得出。局部变量 xi(t) 的 n 阶矩
显然,
的导数得出。局部变量 xi(t) 的 n 阶矩
显然,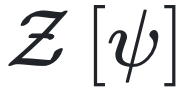 满足
满足 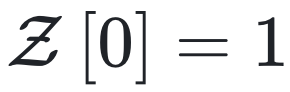 。
在文献 [72] 中,我们计算了对于有限的 c,
。
在文献 [72] 中,我们计算了对于有限的 c, 在由式 (2) 定义的网络集合上的平均值,将问题转化为鞍点积分的求解。更重要的是,我们对序参量给出了清晰的物理解释,简化了鞍点方程,并得到了稀疏区域动力学的可行解。在 N→∞ 的极限情况下,微观动力学变量解耦,单个变量 x(t) 的有效动力学的路径概率
在由式 (2) 定义的网络集合上的平均值,将问题转化为鞍点积分的求解。更重要的是,我们对序参量给出了清晰的物理解释,简化了鞍点方程,并得到了稀疏区域动力学的可行解。在 N→∞ 的极限情况下,微观动力学变量解耦,单个变量 x(t) 的有效动力学的路径概率  由下式确定
其中 δF 是狄拉克 -δ 泛函。宏观可观测量由 m(t) =〈x(t)〉* 和 q(t) =〈x2(t)〉* 计算得出,其中
由下式确定
其中 δF 是狄拉克 -δ 泛函。宏观可观测量由 m(t) =〈x(t)〉* 和 q(t) =〈x2(t)〉* 计算得出,其中
是由  支配下有效动力学的平均量。自洽方程 (7) 是具有局部树状结构的稀疏有向网络 [73] 上一大类模型(见表 I)的精确解,其中入度和出度具有任意分布 pJ 和
支配下有效动力学的平均量。自洽方程 (7) 是具有局部树状结构的稀疏有向网络 [73] 上一大类模型(见表 I)的精确解,其中入度和出度具有任意分布 pJ 和  。在文献 [72] 中,我们处理了在入度和出度相关的网络上具有高斯加性噪声的动力学模型的更一般情况。方程 (7) 的解确定了在 N→∞ 极限下微观变量的全概率分布的时间演化。
。在文献 [72] 中,我们处理了在入度和出度相关的网络上具有高斯加性噪声的动力学模型的更一般情况。方程 (7) 的解确定了在 N→∞ 极限下微观变量的全概率分布的时间演化。
图 1. SIS 模型、LV 模型和 NN 模型的均值 m(t) 和标准差 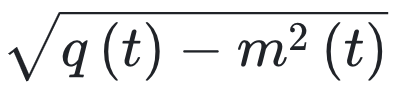 的动态变化(见表 I)。结果展示了平均度为 c = 5 的有向随机网络以及两种入度分布(式 (9))的情况:泊松分布(左列)和几何分布(右列)。耦合强度的分布 pJ 的均值为 μJ ,标准差为σJ = 0.1。对于 LV 模型和 NN 模型,pJ 是高斯分布;对于 SIS 模型,pJ 是均匀分布。实线是使用具有 5×104 条路径和初始条件 xi(0) = 10-3。图中的符号表示对由具有 4000 个节点的模型生成的 10 个随机网络进行数值模拟的结果。这些网络构成了一个集合,模拟过程基于公式(1)展开。垂直条表示宏观可观测量的标准差。
的动态变化(见表 I)。结果展示了平均度为 c = 5 的有向随机网络以及两种入度分布(式 (9))的情况:泊松分布(左列)和几何分布(右列)。耦合强度的分布 pJ 的均值为 μJ ,标准差为σJ = 0.1。对于 LV 模型和 NN 模型,pJ 是高斯分布;对于 SIS 模型,pJ 是均匀分布。实线是使用具有 5×104 条路径和初始条件 xi(0) = 10-3。图中的符号表示对由具有 4000 个节点的模型生成的 10 个随机网络进行数值模拟的结果。这些网络构成了一个集合,模拟过程基于公式(1)展开。垂直条表示宏观可观测量的标准差。
方程 (7) 在形式上与稀疏无序系统研究中出现的其他分布方程相似 [61-66]。因此,我们可以使用群体动力学算法[61,63,64] 对该方程进行数值求解。在该算法的标准版本[61,64]中,概率密度由一组随机变量参数化。在这里,我们通过引入一组动态轨迹来推广该算法以计算  。在每次迭代步骤中,从种群中随机选择一条路径,并根据式 (7) 中的包含狄拉克 –δF 的微分方程进行更新。经过足够的迭代后,路径种群收敛到一个稳态分布,从而为
。在每次迭代步骤中,从种群中随机选择一条路径,并根据式 (7) 中的包含狄拉克 –δF 的微分方程进行更新。经过足够的迭代后,路径种群收敛到一个稳态分布,从而为  提供数值解。该算法的详细说明见文献 [72]。
在图 1 中,我们将式 (7) 的解与有限 N 情况下原始耦合动力学方程 (1) 的数值模拟结果进行了比较。这些图展示了不同网络拓扑结构和表 I 中的三种模型(文献 [1] 中的 NN 模型、LV 模型和流行病传播的 SIS 模型)下微观变量的均值 m(t) 和标准差
提供数值解。该算法的详细说明见文献 [72]。
在图 1 中,我们将式 (7) 的解与有限 N 情况下原始耦合动力学方程 (1) 的数值模拟结果进行了比较。这些图展示了不同网络拓扑结构和表 I 中的三种模型(文献 [1] 中的 NN 模型、LV 模型和流行病传播的 SIS 模型)下微观变量的均值 m(t) 和标准差 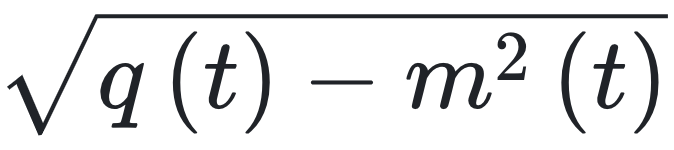 的时间演化。图 1 中的结果是针对泊松入度和几何入度的情况,其中 pin,k 由下式给出
在文献 [72] 中,我们还对另外两种情况将式 (7) 的解与数值模拟结果进行了比较:幂律入度分布网络上的 NN 模型以及流行病阈值下的 SIS 模型。在所有情况下,我们关于 N→∞ 的理论结果与大 N 情况下的数值模拟结果都非常吻合,证实了式 (7) 的精确性。
一个重要的问题是,当 c→∞ [1,4,28,30]时,方程 (7) 是否能恢复全连接模型的解析结果。在热力学极限 N→∞ 之后取极限 c→∞,实际上是在考虑标度机制,其中 c∝Na,且 0 < a < 1 [74 – 77]。我们在文献 [72] 中表明,在极限 c→∞ 下,度的涨落仍然显著,并且
的时间演化。图 1 中的结果是针对泊松入度和几何入度的情况,其中 pin,k 由下式给出
在文献 [72] 中,我们还对另外两种情况将式 (7) 的解与数值模拟结果进行了比较:幂律入度分布网络上的 NN 模型以及流行病阈值下的 SIS 模型。在所有情况下,我们关于 N→∞ 的理论结果与大 N 情况下的数值模拟结果都非常吻合,证实了式 (7) 的精确性。
一个重要的问题是,当 c→∞ [1,4,28,30]时,方程 (7) 是否能恢复全连接模型的解析结果。在热力学极限 N→∞ 之后取极限 c→∞,实际上是在考虑标度机制,其中 c∝Na,且 0 < a < 1 [74 – 77]。我们在文献 [72] 中表明,在极限 c→∞ 下,度的涨落仍然显著,并且  取决于重整化入度 κi = Ki/c(i = 1,… ,N) 的完整分布νin(κ) =δ(κ- 1)。只有当 νin(κ) =δ(κ- 1) 时,才能恢复全连接网络上著名有效动力学。由于度的涨落导致全连接模型普适性的破坏在文献 [74 – 77] 中已被预见。
取决于重整化入度 κi = Ki/c(i = 1,… ,N) 的完整分布νin(κ) =δ(κ- 1)。只有当 νin(κ) =δ(κ- 1) 时,才能恢复全连接网络上著名有效动力学。由于度的涨落导致全连接模型普适性的破坏在文献 [74 – 77] 中已被预见。
为了展示方程 (7) 的优势及其具体应用,我们推导了稀疏有向网络上神经网络模型的相图。在这种情况下,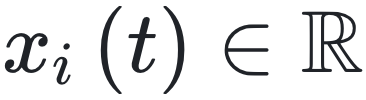 表示神经元 i,f(x) = x 处的突触电流,且 g( {x, x’) = tanh(x’) 。让我们根据 A 的复特征值
表示神经元 i,f(x) = x 处的突触电流,且 g( {x, x’) = tanh(x’) 。让我们根据 A 的复特征值 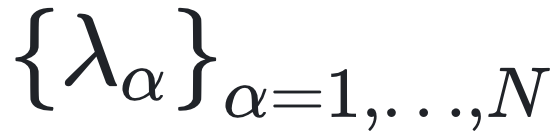 的实部将它们排序为
的实部将它们排序为 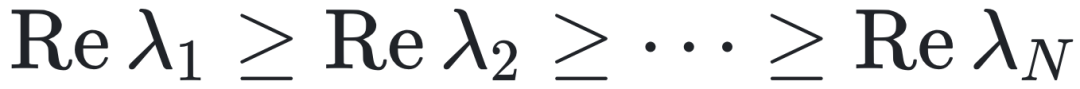 。对方程 (1) 的线性稳定性分析表明,如果
。对方程 (1) 的线性稳定性分析表明,如果 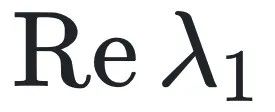 < 1 ,则 x = 0 是稳定的。基于文献 [67-69] 中关于有向网络谱的解析结果,我们发现,只要 c < cstab ,平凡不动点就是稳定的,其中
方程 (10) 中的两种不同状态源于 A 的谱中的能隙-无能隙转变 [67]。对于
< 1 ,则 x = 0 是稳定的。基于文献 [67-69] 中关于有向网络谱的解析结果,我们发现,只要 c < cstab ,平凡不动点就是稳定的,其中
方程 (10) 中的两种不同状态源于 A 的谱中的能隙-无能隙转变 [67]。对于 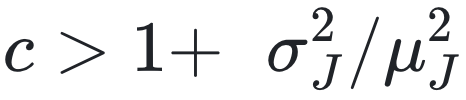 ,当 N→∞ 时,谱隙 |λ1–λ2| 保持有限,而当
,当 N→∞ 时,谱隙 |λ1–λ2| 保持有限,而当 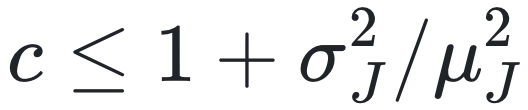 时,谱隙消失。方程 (10) 适用于 μJ > 0 和 c > 1。条件 c > 1 确保具有度分布
时,谱隙消失。方程 (10) 适用于 μJ > 0 和 c > 1。条件 c > 1 确保具有度分布  的有向网络包含一个巨大的强连通分量 [78, 79],这意味着 A 的特征值分布中存在一个连续部分 [68]。
的有向网络包含一个巨大的强连通分量 [78, 79],这意味着 A 的特征值分布中存在一个连续部分 [68]。
图 2. 对于 μJ = 0, μJ > 1 和 0 < μJ < 1 的神经网络(NN)模型的相图 (c, σJ)。平均突触电流 m(t) 分别在相 I 和相 II 中弛豫到平凡和非平凡的不动点。在混沌相 III 和相 IV 中,m(t) 分别围绕零值和非零值呈现非周期性振荡(见图 4)。在 c = 1 处的点划线标记了渗流阈值,而虚线曲线标识了能隙 – 无隙转变。圆圈和菱形表示界定相 IV 的转变线的数值结果(见正文),这些结果是通过求解方程 (7) 得到的,采用群体动力学模拟,考虑 5 ×104 条路径,并假设输入信号遵循泊松分布,选定 μJ(μJ= 1/3 和 μJ = 3/2) 两个参数值。红点标记 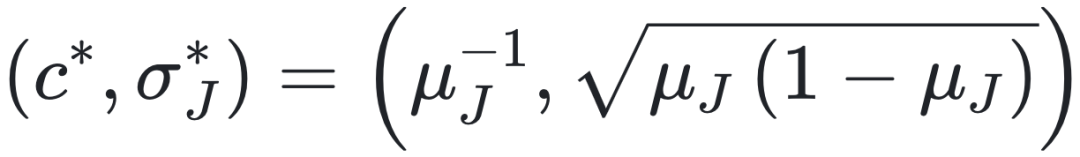 。
。
我们强调,平凡解的线性稳定性分析无法提供关于当 x = 0 变得不稳定时出现的弛豫动力学或稳态解的信息。因此,我们通过求解方程 (7) 来研究 NN 模型的动力学和稳态。图 2 展示了针对不同 μJ 区域得到的相图。在相 I 中,m(t) 以指数级快速弛豫到平凡解 m = 0,而在相 II 中,m(t) 演化到一个非零不动点。在相 III 和相 IV 中,神经网络呈现出混沌活动,其特征是 m(t) [1,30] 的缓慢且非周期性振荡。界定相 I 的稳定线是普适的,因为它们仅取决于 pJ 和 pin,k 的一阶和二阶矩。
图 3 描述了不动点相 I 和相 II 之间的转变。当 c 从上方接近临界平均度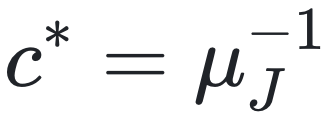 时,非平凡不动点 m=m(t) 连续消失。临界点 c* 与 pin,k 无关,并且 m(t) 在相 I 和相 II 内以指数级快速弛豫。由于临界慢化,方程 (7) 的数值解在 c* 附近的计算要求更高。在相 II 中,神经元放电率演化到具有有限方差的稳态分布。
时,非平凡不动点 m=m(t) 连续消失。临界点 c* 与 pin,k 无关,并且 m(t) 在相 I 和相 II 内以指数级快速弛豫。由于临界慢化,方程 (7) 的数值解在 c* 附近的计算要求更高。在相 II 中,神经元放电率演化到具有有限方差的稳态分布。
图 3. 有向随机网络上 NN 模型的不动点相之间的连续相变。耦合强度遵循均值为 μJ = 1/3、标准差为 σJ = 0.1 的高斯分布。结果使用具有 5×104 条路径的群体动力学从方程 (7) 推导得出。(a) 对于泊松和几何入度(方程 (9)),定点解 m(t) = m 作为 c 的函数。(b) 对于泊松入度和初始条件 xi(0) = 1, m(t)在转变过程中的弛豫动力学。对于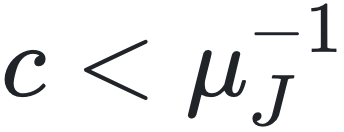 ,当 t→∞ 时, m(t) 其以指数形式弛豫到 m = 0。
,当 t→∞ 时, m(t) 其以指数形式弛豫到 m = 0。
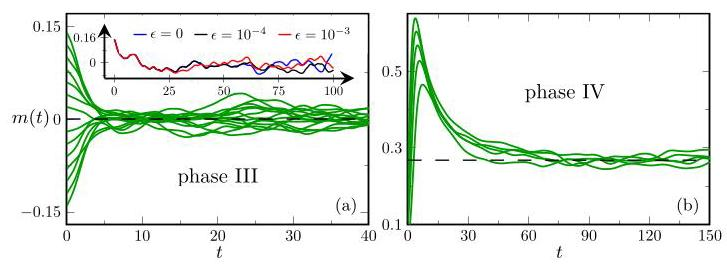
图 4 展示了在几种初始条件下,m(t) 在混沌相的动力学行为。经过一段过渡时间 Ttr 后,m(t) 稳定到一个吸引子上,在相 III 围绕零振荡,在相IV 围绕一个非零值振荡。图 4(a) 的插图展示了 m(t) 对初始条件微小扰动的敏感性,这是确定性混沌的特征 [80]。通过求解方程 (7) 并数值计算时间平均值 [81]。
对于 ,我们估计了界定相 IV 的相变线 [72]。对于 T→∞,相 II 和相IV 之间的相变由 Δ 决定,因为在不动点相Δ = 0,在混沌相 Δ > 0。参数 M 区分了混沌相:在相III 中 M = 0,在相 IV 中 M≠0(见图 4)。我们关于相 III 和相 IV 之间相变的数值结果与图 2 中的虚线一致,这表明这种相变由网络谱中的间隙 |λ1–λ2| 控制。然而,对于 c→∞,向混沌相 III 的这种相变与能隙 – 无能隙转变 [30] 略有偏差,特别是对于较大的 μJ。
,我们估计了界定相 IV 的相变线 [72]。对于 T→∞,相 II 和相IV 之间的相变由 Δ 决定,因为在不动点相Δ = 0,在混沌相 Δ > 0。参数 M 区分了混沌相:在相III 中 M = 0,在相 IV 中 M≠0(见图 4)。我们关于相 III 和相 IV 之间相变的数值结果与图 2 中的虚线一致,这表明这种相变由网络谱中的间隙 |λ1–λ2| 控制。然而,对于 c→∞,向混沌相 III 的这种相变与能隙 – 无能隙转变 [30] 略有偏差,特别是对于较大的 μJ。
我们发展了稀疏有向网络上复杂系统的动力学平均场理论,推导出了在极限 N→∞ 下有效动力学的精确路径概率方程。与具有双向边的稀疏模型 [38, 39] 不同,我们的路径概率方程可以使用群体动力学进行数值求解 [64]。通过与流行病传播、神经网络和生态系统研究中基本模型的数值模拟进行比较,我们验证了我们一般解的精确性。最后,我们应用我们的解来确定 [1, 30] 典型神经网络模型的稀疏有向版本的完整相图。
图 4. 对于具有泊松入度和均值为 μJ = 1/3 的高斯分布 pJ 的有向网络,在混沌相内 m(t) 的动力学。结果使用具有 5×104 条路径和多个初始条件的群体动力学对公式 (7) 的求解。虚线表示 M 的值,即公式 (11),它表征了每个相的混沌吸引子。(a) c = 2.5 和 σJ = 2。插图:从单个网络实例 (N = 4000)、初始条件 xi(0) = 0.15 – ϵ 和不同的 ϵ 的确定性公式 (1) 得到 m(t) 的动力学。(b) c = 5 和 σJ= 0.62。
公式 (7) 的数值解不需要从配置模型 [71] 生成网络,与在网络上对方程 (1) 进行大规模模拟 [22] 相比,具有一定的计算优势。除了其数值应用外,公式 (7) 为研究稳态 [4]、计算关联函数 [3]、推导宏观序参量的近似动力学方程以及开发系统的微扰方法 [26, 82] 提供了一个基础框架。
我们的工作为探索稀疏异质网络在生态系统动力学、耦合振子、流行病传播等领域中的作用铺平了道路。未来的工作包括确定稀疏 Lotka-Volterra 模型的相图 [7]、外部噪声对相图的影响 [29] 以及网络异质性在复杂系统临界指数 [77, 83] 中的作用。最后,将当前的形式体系与文献 [84] 中的空腔方法联系起来将是很有意义的。
[1] H. Sompolinsky, A. Crisanti, and H. J. Sommers, “Chaos in random neural networks,” Phys. Rev. Lett. 61, 259- 262 (1988).
[2] Jonathan Kadmon and Haim Sompolinsky, “Transition to chaos in random neuronal networks,” Phys. Rev. X 5, 041030 (2015).
[3] Daniel Martí, Nicolas Brunel, and Srdjan Ostojic, “Correlations between synapses in pairs of neurons slow down dynamics in randomly connected neural networks,” Phys. Rev. E 97, 062314 (2018).
[4] A. Crisanti and H. Sompolinsky, “Path integral approach to random neural networks,” Phys. Rev. E 98, 062120 (2018).
[5] Carles Martorell, Rubén Calvo, Alessia Annibale, and Miguel A. Muñoz, “Dynamically selected steady states and criticality in non-reciprocal networks,” Chaos, Solitons and Fractals 182, 114809 (2024).
[6] Manfred Opper and Sigurd Diederich, “Phase transition and $$1/mathrm{f$$ noise in a game dynamical model,” Phys. Rev. Lett. 69, 1616-1619 (1992).
[7] Guy Bunin, “Ecological communities with lotka-volterra dynamics,” Phys. Rev. E 95, 042414 (2017).
[8] Ada Altieri, Felix Roy, Chiara Cammarota, and Giulio Biroli, “Properties of equilibria and glassy phases of the random lotka-volterra model with demographic noise,” Phys. Rev. Lett. 126, 258301 (2021).
[9] Angélica S. Mata and Silvio C. Ferreira, “Pair quenched mean-field theory for the susceptible-infected-susceptible model on complex networks,” Europhysics Letters 103, 48003 (2013).
[10] P. Van Mieghem, “Epidemic phase transition of the sis type in networks,” Europhysics Letters 97, 48004 (2012).
[11] A. V. Goltsev, S. N. Dorogovtsev, J. G. Oliveira, and J. F. F. Mendes, “Localization and spreading of diseases in complex networks,” Phys. Rev. Lett. 109, 128702 (2012).
[12] Romualdo Pastor-Satorras, Claudio Castellano, Piet Van Mieghem, and Alessandro Vespignani, “Epidemic processes in complex networks,” Rev. Mod. Phys. 87, 925-979 (2015).
[13] J. C. Stiller and G. Radons, “Dynamics of nonlinear oscillators with random interactions,” Phys. Rev. E 58, 1789- 1799 (1998).
[14] Francisco A. Rodrigues, Thomas K. DM. Peron, Peng Ji, and Jürgen Kurths, “The kuramoto model in complex networks,” Physics Reports 610, 1-98 (2016), the Kuramoto model in complex networks.
[15] Axel Prüser, Sebastian Rosmej, and Andreas Engel, “Nature of the volcano transition in the fully disordered kuramoto model,” Phys. Rev. Lett. 132, 187201 (2024).
[16] Fabian Baumann, Philipp Lorenz-Spreen, Igor M. Sokolov, and Michele Starnini, “Modeling echo chambers and polarization dynamics in social networks,” Phys. Rev. Lett. 124, 048301 (2020).
[17] Fabian Baumann, Philipp Lorenz-Spreen, Igor M. Sokolov, and Michele Starnini, “Emergence of polarized ideological opinions in multidimensional topic spaces,” Phys. Rev. X 11, 011012 (2021).
[18] Claude Godrèche and Jean-Marc Luck, “Characterising the nonequilibrium stationary states of orn-stein-uhlenbeck processes,” Journal of Physics A: Mathematical and Theoretical 52, 035002 (2018).
[19] Andrea Crisanti and Matteo Paoluzzi, “Most probable path of active ornstein-uhlenbeck particles,” Phys. Rev. E 107, 034110 (2023).
[20] Francesco Ferraro, Christian Grilletta, Amos Maritan, Samir Suweis, and Sandro Azaele, “Exact solution of dynamical mean-field theory for a linear system with annealed disorder,” (2024), arXiv:2405.05183 [cond-mat.dis-nn].
[21] I.Z. Kiss, J.C. Miller, and P.L. Simon, Mathematics of Epidemics on Networks: From Exact to Approximate Models, Interdisciplinary Applied Mathematics (Springer International Publishing, 2017).
[22] Diogo H. Silva, Francisco A. Rodrigues, and Silvio C. Ferreira, “High prevalence regimes in the pair-quenched mean-field theory for the susceptible-infected-susceptible model on networks,” Phys. Rev. E 102, 012313 (2020).
[23] V. Thibeault, A. Allard, and P. Desrosiers, “The low-rank hypothesis of complex systems,” Nat. Phys. 20, 294-302 (2024).
[24] P. C. Martin, E. D. Siggia, and H. A. Rose, “Statistical dynamics of classical systems,” Phys. Rev. A 8, 423-437 (1973).
[25] A.C.C. Coolen, “Chapter 15 statistical mechanics of recurrent neural networks ii – dynamics,” in Neuro-Informatics and Neural Modelling, Handbook of Biological Physics, Vol. 4, edited by F. Moss and S. Gielen (North-Holland, 2001) pp. 619-684.
[26] John A Hertz, Yasser Roudi, and Peter Sollich, “Path integral methods for the dynamics of stochastic and disordered systems,” Journal of Physics A: Mathematical and Theoretical 50, 033001 (2016).
[27] F Roy, G Biroli, G Bunin, and C Cammarota, “Numerical implementation of dynamical mean field theory for disordered systems: application to the lotka-volterra model of ecosystems,” Journal of Physics A: Mathematical and Theoretical 52, 484001 (2019).
[28] Tobias Galla, “Dynamically evolved community size and stability of random lotka-volterra ecosystems(a),” Euro-physics Letters 123, 48004 (2018).
[29] Jannis Schuecker, Sven Goedeke, and Moritz Helias, “Optimal sequence memory in driven random networks,” Phys. Rev. X 8, 041029 (2018).
[30] Francesca Mastrogiuseppe and Srdjan Ostojic, “Linking connectivity, dynamics, and computations in low-rank recurrent neural networks,” Neuron 99, 609-623.e29 (2018).
[31] Lyle Poley, Joseph W. Baron, and Tobias Galla, “Generalized lotka-volterra model with hierarchical interactions,” Phys. Rev. E 107, 024313 (2023).
[32] Fabián Aguirre-López, “Heterogeneous mean-field analysis of the generalized lotka-volterra model on a network,” Journal of Physics A: Mathematical and Theoretical 57, 345002 (2024).
[33] Jong Il Park, Deok-Sun Lee, Sang Hoon Lee, and Hye Jin Park, “Incorporating heterogeneous interactions for ecological biodiversity,” Phys. Rev. Lett. 133, 198402 (2024).
[34] Tuan Minh Pham and Kunihiko Kaneko, “Dynamical theory for adaptive systems,” Journal of Statistical Mechanics: Theory and Experiment 2024, 113501 (2024).
[35] Valentina Ros, Felix Roy, Giulio Biroli, and Guy Bunin, “Quenched complexity of equilibria for asymmetric generalized lotka-volterra equations,” Journal of Physics A: Mathematical and Theoretical 56, 305003 (2023).
[36] M. Newman, Networks: An Introduction (OUP Oxford, 2010).
[37] Paulo R. Guimarães, “The structure of ecological networks across levels of organization,” Annual Review of Ecology, Evolution, and Systematics 51, 433-460 (2020).
[38] J P L Hatchett, B Wemmenhove, I Pérez Castillo, T Nikoletopoulos, N S Skantzos, and A C C Coolen, “Parallel dynamics of disordered ising spin systems on finitely connected random graphs,” Journal of Physics A: Mathematical and General 37, 6201 (2004).
[39] I Neri and D Bollé, “The cavity approach to parallel dynamics of ising spins on a graph,” Journal of Statistical Mechanics: Theory and Experiment 2009, P08009 (2009).
[40] Kazushi Mimura and A C C Coolen, “Parallel dynamics of disordered ising spin systems on finitely connected directed random graphs with arbitrary degree distributions,” Journal of Physics A: Mathematical and Theoretical 42, 415001 (2009).
[41] Yasser Roudi and John Hertz, “Dynamical tap equations for non-equilibrium ising spin glasses,” Journal of Statistical Mechanics: Theory and Experiment 2011, P03031 (2011).
[42] Erik Aurell and Hamed Mahmoudi, “Dynamic mean-field and cavity methods for diluted ising systems,” Phys. Rev. E 85, 031119 (2012).
[43] P. Zhang, “Inference of kinetic ising model on sparse graphs,” J. Stat. Phys. 148, 502-512 (2012).
[44] Gino Del Ferraro and Erik Aurell, “Dynamic message-passing approach for kinetic spin models with reversible dynamics,” Phys. Rev. E 92, 010102 (2015).
[45] E. Aurell, G. Del Ferraro, E. Domínguez, and R. Mulet, “Cavity master equation for the continuous time dynamics of discrete-spin models,” Phys. Rev. E 95, 052119 (2017).
[46] Eduardo Domínguez Vázquez, Gino Del Ferraro, and Federico Ricci-Tersenghi, “A simple analytical description of the non-stationary dynamics in ising spin systems,” Journal of Statistical Mechanics: Theory and Experiment 2017, 033303 (2017).
[47] Giuseppe Torrisi, Alessia Annibale, and Reimer Kühn, “Overcoming the complexity barrier of the dynamic message-passing method in networks with fat-tailed degree distributions,” Phys. Rev. E 104, 045313 (2021).
[48] Giuseppe Torrisi, Reimer Kühn, and Alessia Annibale, “Uncovering the non-equilibrium stationary properties in sparse boolean networks,” Journal of Statistical Mechanics: Theory and Experiment 2022, 053303 (2022).
[49] Freya Behrens, Barbora Hudcová, and Lenka Zdeborová, “Backtracking dynamical cavity method,” Phys. Rev. X 13, 031021 (2023).
[50] Freya Behrens, Barbora Hudcová, and Lenka Zde-borová, “Dynamical phase transitions in graph cellular automata,” Phys. Rev. E 109, 044312 (2024).
[51] B. Derrida, E. Gardner, and A. Zippelius, “An exactly solvable asymmetric neural network model,” Europhysics Letters 4, 167 (1987).
[52] Malbor Asllani, Renaud Lambiotte, and Timoteo Carletti, “Structure and dynamical behavior of nonnormal networks,” Science Advances 4, eaau9403 (2018), https://www.science.org/doi/pdf/10.1126/sciadv.aau9403.
[53] Yangfan Peng, Antje Bjelde, Pau Vilimelis Aceituno, Franz X. Mittermaier, Henrike Planert, Sabine Grosser, Julia Onken, Katharina Faust, Thilo Kalbhenn, Matthias Simon, Helena Radbruch, Pawel Fidzinski, Dietmar Schmitz, Henrik Alle, Martin Holtkamp, Imre Vida, Benjamin F. Grewe, and Jörg R. P. Geiger, “Directed and acyclic synaptic connectivity in the human layer 2-3 cortical microcircuit,” Science 384, 338-343 (2024), https://www.science.org/doi/pdf/10.1126/science.adg8828.
[54] Jennifer A. Dunne, Richard J. Williams, and Neo D. Martinez, “Food-web structure and network theory: The role of connectance and size,” Proceedings of the National Academy of Sciences 99, 12917-12922 (2002), https://www.pnas.org/doi/pdf/10.1073/pnas.192407699.
[55] Jordi Bascompte, “Disentangling the web of life,” Science 325, 416-419 (2009), https://www.science.org/doi/pdf/10.1126/science.1170749.
[56] S. S. Shen-Orr, R. Milo, S. Mangan, and U. Alon, “Network motifs in the transcriptional regulation network of escherichia coli,” Nat. Genet. 31, 64-68 (2002).
[57] Tong Ihn Lee, Nicola J. Rinaldi, François Robert, Duncan T. Odom, Ziv Bar-Joseph, Georg K. Gerber, Nancy M. Hannett, Christopher T. Harbison, Craig M. Thompson, Itamar Simon, Julia Zeitlinger, Ezra G. Jennings, Heather L. Murray, D. Benjamin Gordon, Bing Ren, John J. Wyrick, Jean-Bosco Tagne, Thomas L. Volkert, Ernest Fraenkel, David K. Gifford, and Richard A. Young, “Transcriptional regulatory networks in saccharomyces cerevisiae,” Science 298, 799-804 (2002), https://www.science.org/doi/pdf/10.1126/science.1075090.
[58] Haewoon Kwak, Changhyun Lee, Hosung Park, and Sue Moon, “What is twitter, a social network or a news media?” in Proceedings of the 19th International Conference on World Wide Web (Association for Computing Machinery, New York, NY, USA, 2010) p. 591-600.
[59] Christoph Schweimer, Christine Gfrerer, Florian Lug-stein, David Pape, Jan A. Velimsky, Robert Elsässer, and Bernhard C. Geiger, “Generating simple directed social network graphs for information spreading,” (Association for Computing Machinery, New York, NY, USA, 2022) p. 1475-1485.
[60] R. Pastor-Satorras and A. Vespignani, Evolution and Structure of the Internet: A Statistical Physics Approach (Cambridge University Press, 2004).
[61] M Mézard and G Parisi, “The bethe lattice spin glass revisited,” Eur. Phys. J. B 20, 217-233 (2001).
[62] M Mézard and G Parisi, “The cavity method at zero temperature,” J. Stat. Phys. 111, 1-34 (2003).
[63] Reimer Kühn, “Spectra of sparse random matrices,” Journal of Physics A: Mathematical and Theoretical 41, 295002 (2008).
[64] Fernando Lucas Metz, Izaak Neri, and Tim Rogers, “Spectral theory of sparse non-hermitian random matrices,” Journal of Physics A: Mathematical and Theoretical 52, 434003 (2019).
[65] R Abou-Chacra, D J Thouless, and P W Anderson, “A selfconsistent theory of localization,” Journal of Physics C: Solid State Physics 6, 1734 (1973).
[66] M. Mézard and A. Montanari, Information, Physics, and Computation, Oxford Graduate Texts (OUP Oxford, 2009).
[67] Izaak Neri and Fernando Lucas Metz, “Eigenvalue outliers of non-hermitian random matrices with a local tree structure,” Phys. Rev. Lett. 117, 224101 (2016).
[68] Izaak Neri and Fernando Lucas Metz, “Linear stability analysis of large dynamical systems on random directed graphs,” Phys. Rev. Res. 2, 033313 (2020).
[69] Fernando Lucas Metz and Izaak Neri, “Localization and universality of eigenvectors in directed random graphs,” Phys. Rev. Lett. 126, 040604 (2021).
[70] M. E. J. Newman, S. H. Strogatz, and D. J. Watts, “Random graphs with arbitrary degree distributions and their applications,” Phys. Rev. E 64, 026118 (2001).
[71] Bailey K. Fosdick, Daniel B. Larremore, Joel Nishimura, and Johan Ugander, “Configuring random graph models with fixed degree sequences,” SIAM Review 60, 315-355 (2018), https://doi.org/10.1137/16M1087175.
[72] See the Supplemental Material for all derivations of DMFT and a detailed account of the population dynamics algorithm.
[73] Charles Bordenave and Marc Lelarge, “Resolvent of large random graphs,” Random Structures & Algorithms 37, 332-352 (2010), https://onlinelibrary.wiley.com/doi/pdf/10.1002/rsa.20313.
[74] Fernando L. Metz and Jeferson D. Silva, “Spectral density of dense random networks and the breakdown of the wigner semicircle law,” Phys. Rev. Res. 2, 043116 (2020).
[75] Fernando L Metz and Thomas Peron, “Mean-field theory of vector spin models on networks with arbitrary degree distributions,” Journal of Physics: Complexity 3, 015008 (2022).
[76] Jeferson D Silva and Fernando L Metz, “Analytic solution of the resolvent equations for heterogeneous random graphs: spectral and localization properties,” Journal of Physics: Complexity 3, 045012 (2022).
[77] Leonardo S. Ferreira and Fernando L. Metz, “Nonequilibrium dynamics of the ising model on heterogeneous networks with an arbitrary distribution of threshold noise,” Phys. Rev. E 107, 034127 (2023).
[78] G. Timár, A. V. Goltsev, S. N. Dorogovtsev, and J. F. F. Mendes, “Mapping the structure of directed networks: Beyond the bow-tie diagram,” Phys. Rev. Lett. 118, 078301 (2017).
[79] Ivan Kryven, “Emergence of the giant weak component in directed random graphs with arbitrary degree distributions,” Phys. Rev. E 94, 012315 (2016).
[80] G.L. Baker and J.P. Gollub, Chaotic Dynamics: An Introduction (Cambridge University Press, 1996).
[81] Maximilian Gelbrecht, Jürgen Kurths, and Frank Hell-mann, “Monte carlo basin bifurcation analysis,” New Journal of Physics 22, 033032 (2020).
[82] F. L. Metz, G. Parisi, and L. Leuzzi, “Finite-size corrections to the spectrum of regular random graphs: An analytical solution,” Phys. Rev. E 90, 052109 (2014).
[83] Thibaut Arnoulx de Pirey and Guy Bunin, “Critical behavior of a phase transition in the dynamics of interacting populations,” (2024), arXiv:2402.05063 [cond-mat.stat-mech].
[84] Mattia Tarabolo and Luca Dall’Asta, “Gaussian approximation of dynamic cavity equations for linearly-coupled stochastic dynamics,” (2024), arXiv:2406.14200 [cond-mat.dis-nn].
人类大脑是一个由数以百亿计的神经元相互连接所构成的复杂系统,被认为是「已知宇宙中最复杂的物体」。本着促进来自神经科学、系统科学、信息科学、物理学、数学以及计算机科学等不同领域,对脑科学、类脑智能与计算、人工智能感兴趣的学术工作者的交流与合作,集智俱乐部联合国内外多所知名高校的专家学者发起神经、认知、智能系列读书会第三季——「计算神经科学」读书会,涵盖复杂神经动力学、神经元建模与计算、跨尺度神经动力学、计算神经科学与AI的融合四大模块,并希望探讨计算神经科学对类脑智能和人工智能的启发。读书会已完结,现在报名可加入社群并解锁回放视频权限。
详情请见:计算神经科学读书会启动:从复杂神经动力学到类脑人工智能
集智俱乐部联合合肥工业大学物理系教授李明、同济大学副教授张毅超、北京师范大学特聘副研究员史贵元与在读博士生邱仲普、张章共同发起「复杂网络动力学」读书会。本次读书会将探讨:同步相变的临界性、如何普适地刻画多稳态与临界点、如何识别并预测临界转变、如何通过局部干预来调控系统保持或回到期望稳态、爆炸逾渗临界行为的关键特征、不同类型的级联过程对逾渗相变的影响有何异同、高阶相互作用的影响能否等效为若干简单机制的叠加、如何有效地促进人类个体间的合作等问题。
读书会计划从3月7日开始,每周五晚19:30-21:30进行,持续8-10周。诚挚邀请领域内研究者、寻求跨领域融合的研究者加入,共同探讨。
6. 探索者计划 | 集智俱乐部2025内容团队招募(全职&兼职)

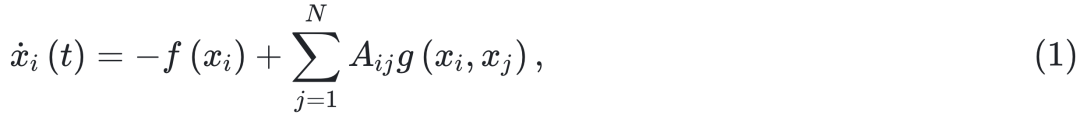
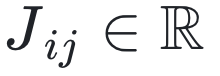 控制相互作用强度。如果 Cij = 1,则存在一条从节点 j 指向 i 的有向边 j→i,否则 Cij = 0。入度
控制相互作用强度。如果 Cij = 1,则存在一条从节点 j 指向 i 的有向边 j→i,否则 Cij = 0。入度 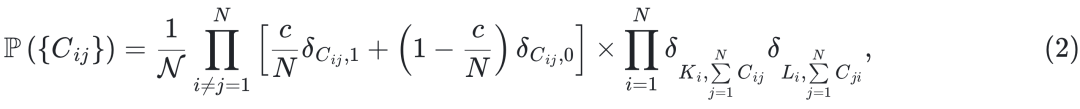
 中抽取的独立同分布随机变量,其中 pin,k 和
中抽取的独立同分布随机变量,其中 pin,k 和  分别是入度和出度分布 [36,64]。参数 c 是平均度
分别是入度和出度分布 [36,64]。参数 c 是平均度
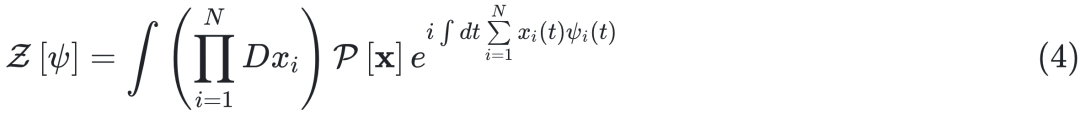
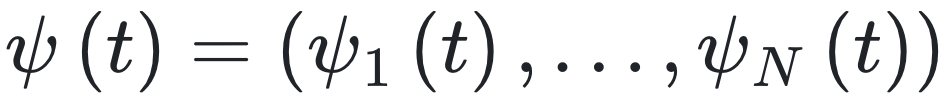 的导数得出。局部变量 xi(t) 的 n 阶矩
的导数得出。局部变量 xi(t) 的 n 阶矩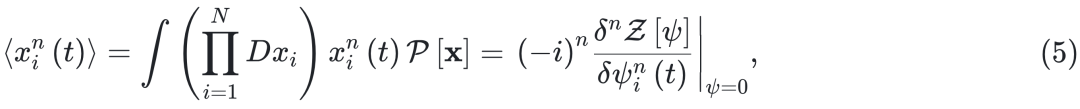
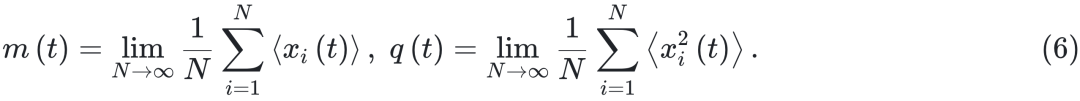
 。
。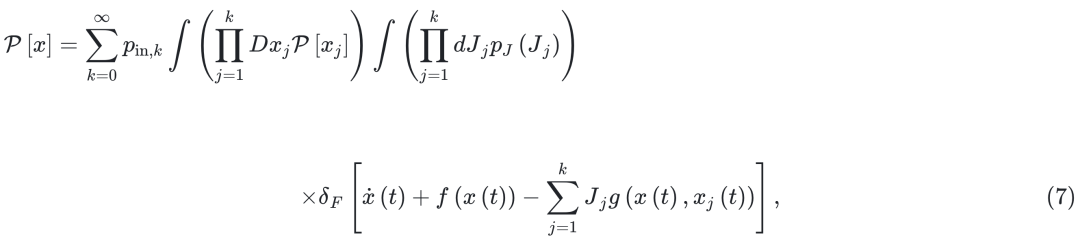
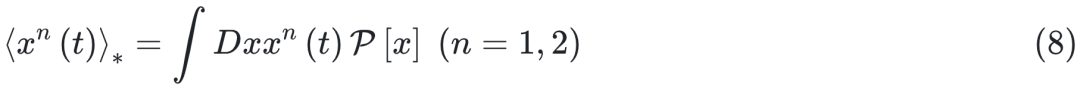
 。在文献 [72] 中,我们处理了在入度和出度相关的网络上具有高斯加性噪声的动力学模型的更一般情况。方程 (7) 的解确定了在 N→∞ 极限下微观变量的全概率分布的时间演化。
。在文献 [72] 中,我们处理了在入度和出度相关的网络上具有高斯加性噪声的动力学模型的更一般情况。方程 (7) 的解确定了在 N→∞ 极限下微观变量的全概率分布的时间演化。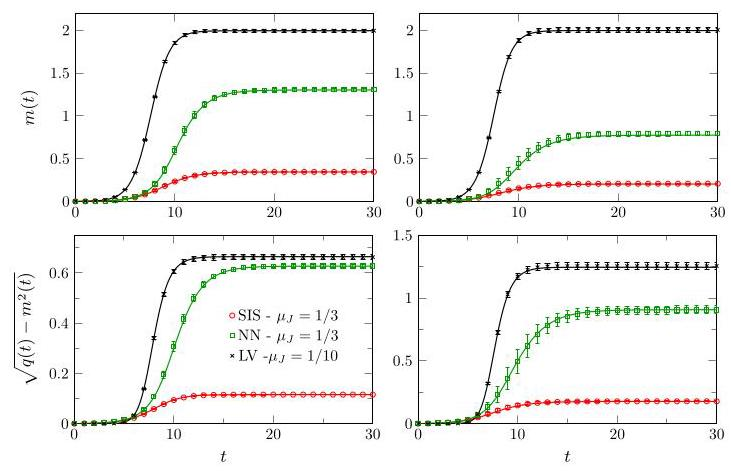
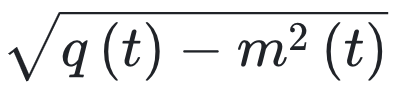 的动态变化(见表 I)。结果展示了平均度为 c = 5 的有向随机网络以及两种入度分布(式 (9))的情况:泊松分布(左列)和几何分布(右列)。耦合强度的分布 pJ 的均值为 μJ ,标准差为σJ = 0.1。对于 LV 模型和 NN 模型,pJ 是高斯分布;对于 SIS 模型,pJ 是均匀分布。实线是使用具有 5×104 条路径和初始条件 xi(0) = 10-3。图中的符号表示对由具有 4000 个节点的模型生成的 10 个随机网络进行数值模拟的结果。这些网络构成了一个集合,模拟过程基于公式(1)展开。垂直条表示宏观可观测量的标准差。
的动态变化(见表 I)。结果展示了平均度为 c = 5 的有向随机网络以及两种入度分布(式 (9))的情况:泊松分布(左列)和几何分布(右列)。耦合强度的分布 pJ 的均值为 μJ ,标准差为σJ = 0.1。对于 LV 模型和 NN 模型,pJ 是高斯分布;对于 SIS 模型,pJ 是均匀分布。实线是使用具有 5×104 条路径和初始条件 xi(0) = 10-3。图中的符号表示对由具有 4000 个节点的模型生成的 10 个随机网络进行数值模拟的结果。这些网络构成了一个集合,模拟过程基于公式(1)展开。垂直条表示宏观可观测量的标准差。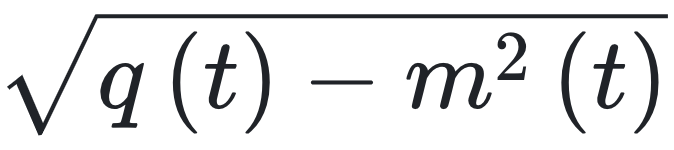 的时间演化。图 1 中的结果是针对泊松入度和几何入度的情况,其中 pin,k 由下式给出
的时间演化。图 1 中的结果是针对泊松入度和几何入度的情况,其中 pin,k 由下式给出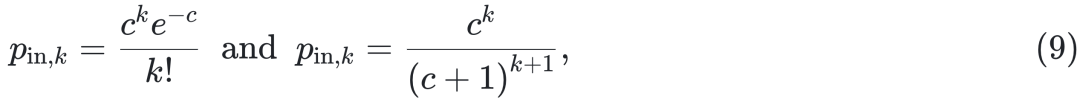
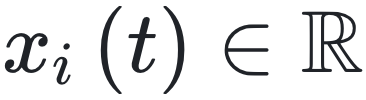 表示神经元 i,f(x) = x 处的突触电流,且 g( {x, x’) = tanh(x’) 。让我们根据 A 的复特征值
表示神经元 i,f(x) = x 处的突触电流,且 g( {x, x’) = tanh(x’) 。让我们根据 A 的复特征值 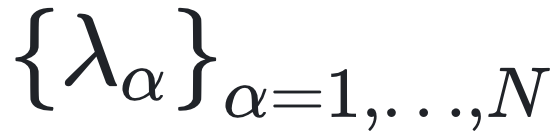 的实部将它们排序为
的实部将它们排序为 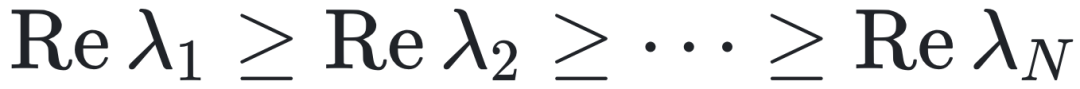 。对方程 (1) 的线性稳定性分析表明,如果
。对方程 (1) 的线性稳定性分析表明,如果 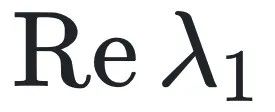 < 1 ,则 x = 0 是稳定的。基于文献 [67-69] 中关于有向网络谱的解析结果,我们发现,只要 c < cstab ,平凡不动点就是稳定的,其中
< 1 ,则 x = 0 是稳定的。基于文献 [67-69] 中关于有向网络谱的解析结果,我们发现,只要 c < cstab ,平凡不动点就是稳定的,其中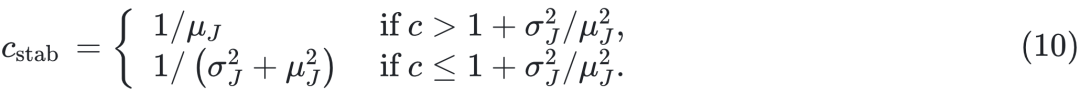
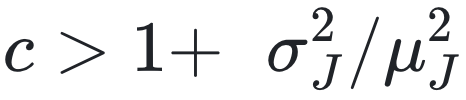 ,当 N→∞ 时,谱隙 |λ1–λ2| 保持有限,而当
,当 N→∞ 时,谱隙 |λ1–λ2| 保持有限,而当 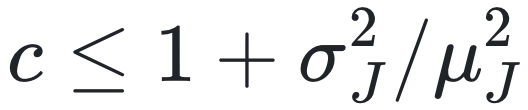 时,谱隙消失。方程 (10) 适用于 μJ > 0 和 c > 1。条件 c > 1 确保具有度分布
时,谱隙消失。方程 (10) 适用于 μJ > 0 和 c > 1。条件 c > 1 确保具有度分布  的有向网络包含一个巨大的强连通分量 [78, 79],这意味着 A 的特征值分布中存在一个连续部分 [68]。
的有向网络包含一个巨大的强连通分量 [78, 79],这意味着 A 的特征值分布中存在一个连续部分 [68]。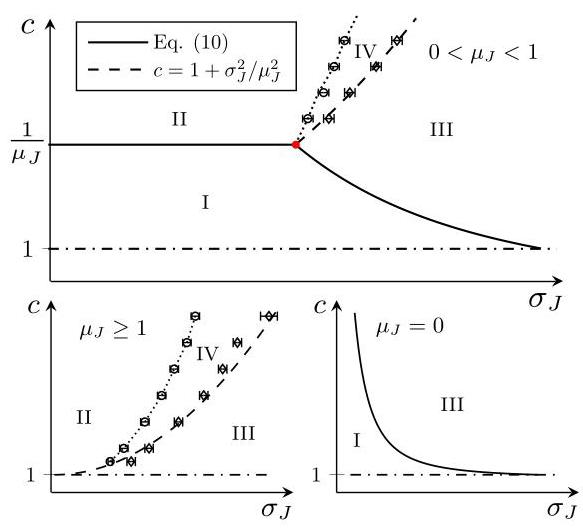
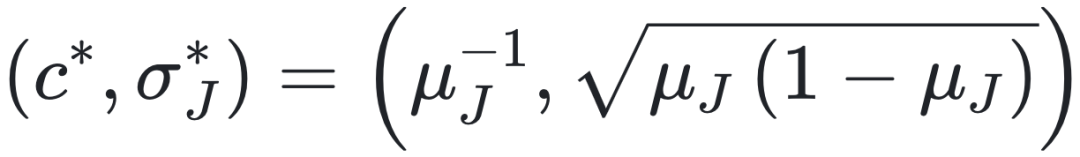 。
。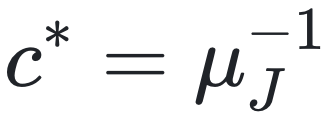 时,非平凡不动点 m=m(t) 连续消失。临界点 c* 与 pin,k 无关,并且 m(t) 在相 I 和相 II 内以指数级快速弛豫。由于临界慢化,方程 (7) 的数值解在 c* 附近的计算要求更高。在相 II 中,神经元放电率演化到具有有限方差的稳态分布。
时,非平凡不动点 m=m(t) 连续消失。临界点 c* 与 pin,k 无关,并且 m(t) 在相 I 和相 II 内以指数级快速弛豫。由于临界慢化,方程 (7) 的数值解在 c* 附近的计算要求更高。在相 II 中,神经元放电率演化到具有有限方差的稳态分布。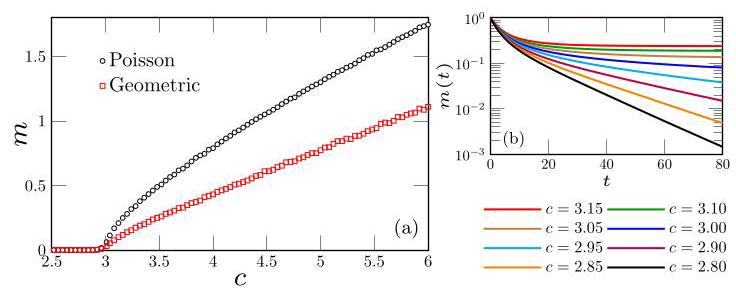
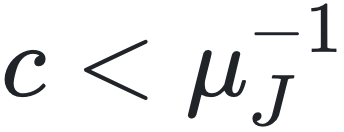 ,当 t→∞ 时, m(t) 其以指数形式弛豫到 m = 0。
,当 t→∞ 时, m(t) 其以指数形式弛豫到 m = 0。