什么是三元闭包 | 集智百科

本文是对集智百科中“三元闭包”词条的摘录,参考资料及相关词条请参阅百科词条原文。
本词条由集智俱乐部众包生产,难免存在纰漏和问题,欢迎大家留言反馈或者前往对应的百科词条页面进行修改,一经修改,可以获得对应的积分奖励噢!
目录
一、什么是三元闭包
二、历史
三、测量
四、方法
五、形成与影响
六、强三元闭包性质和局部桥
七、集智百科词条志愿者招募
三元闭包: https://wiki.swarma.org/index.php?title=三元闭包_Triadic_closure
1. 什么是三元闭包
三元闭包 Triadic closure是社会网络 social network 理论中的概念,最早由德国社会学家格奥尔格·齐美尔 Georg Simmel 在其1908年的著作《社会学:社会形式的调查 》Sociology: Investigations on the Forms of Sociation 中提出。
三元闭包指的是由A,B,C三个节点 node 所组成的三元组的一种性质,即如果A-B和A-C之间存在强联系,则B-C之间也仅存在强联系。这一性质过于极端,以至于它难以在规模较大、结构复杂的网络中被满足,然而在理解网络与网络预测等方面,它却是一种十分有用的对现实的简化。
2. 历史
马克·格兰诺维特 Mark Granovetter 在1973年发表的《弱联系的力量》The Strength of Weak Ties 一文使得三元闭包性质变得流行。在文中,他综合了弗里茨·海德 Fritz Heider 于1946年提出的认知平衡理论 cognitive balance 以及齐美尔对社会网络的理解。
认知平衡是指两个个体倾向于对同一事物产生相同感觉。如果三个个体所组成的三元组没有闭合,那么与同一个体联系的其余两个个体均将想要闭合这一三元组,进而在关系网络中形成闭包。
3.测量
4. 方法
聚集系数
测量三元闭包是否出现的方法之一是聚集系数。节点A的聚集系数,即A的任意两个朋友彼此也是朋友的概率。换句话说,A的聚集系数,就是与A相邻节点之间边的实际数量,与A相邻节点对的个数之比。节点聚集系数取值范围一般在[0, 1]。其详细定义如下所示:
5.形成与影响
在一个信任网络中,三元闭包性质的出现往往是由于传递性。如果节点A信任节点B,并且节点B信任节点C,则节点A将具有信任节点C的基础。在社会网络中,强三元闭包 strong triadic closure 性质的出现往往是由于节点A与节点C拥有共同邻居节点B,在此情况下,节点A与节点C相遇的机会将会增加,进而至少产生一条弱联系。此外,由于两段分离的关系所带来的潜在压力,节点B也具有将节点A和节点C聚在一起的动机。
遵循此原理的网络将高度互连且具有极高的聚集系数。与此相反,不遵循该原理的网络的连通性则较差,且一旦包含负面关系,网络则可能会变得较不稳定。
三元闭包是分析网络如何随时间演变的一个良好模型。简单图论倾向于在某个时点分析网络,而应用三元闭包原理则可以预测网络中联系的形成,以及网络连通性的发展。
在社会网络中,三元闭包将促进合作行为,但是在新联系是通过现存联系而产生的情况下,平均而言个体所拥有的合作伙伴相对数量将小于个体在总体中随机选择合作伙伴时所拥有的合作伙伴相对数量。
这一现象的产生可以从结构与信息两个角度进行解释。基于结构角度而言,网络具有高度聚集性的倾向。基于信息角度而言,我们通常假设,相较于随机的陌生人,个体对朋友的朋友了解更多。
6.强三元闭包性质和捷径
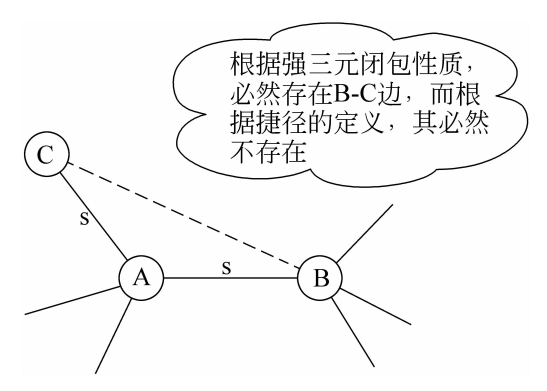
强三元闭包性质指,如果一个节点与两个邻居具有强联系,则这些邻居之间必须至少有一条弱联系。另一方面,当某节点在两个互不相连的邻居间充当中间人 Gatekeeper 时,则将产生捷径 local bridge。
结论是:在遵循强三元闭包性质的网络中,捷径涉及的节点之间的联系必然至少包括一条弱联系。
可以用反证法证明上述结论。假设节点A是节点B和C之间的捷径,根据捷径定义,B和C之间没有弱联系。如果A与B、A与C之间均具有强联系,则根据强三元闭包定义,节点B和C之间将形成弱联系。但是,这与A是捷径的事实相矛盾。因此,捷径两端至少一个节点需要是弱联系。
7.百科项目志愿者招募
作为集智百科项目团队的成员,本文内容由薄荷参与编辑贡献。我们也为每位作者和志愿者准备了专属简介和个人集智百科主页,更多信息可以访问其集智百科个人主页。


在这里从复杂性知识出发与伙伴同行,同时我们希望有更多志愿者加入这个团队,使百科词条内容得到扩充,并为每位志愿者提供相应奖励与资源,建立个人主页与贡献记录,使其能够继续探索复杂世界。
如果你有意参与更加系统精细的分工,扫描二维码填写报名表,我们期待你的加入!

来源:集智百科 审校:LUX 编辑:曾祥轩










