张量网络与神经网络在物理学中的应用和交融

导语

基于张量网络的数值重正化群方法，被广泛地应用到物理学的研究中，已经成为量子多体计算方法大家庭的重要一员。近年来，基于神经网络的机器学习方法也逐渐渗透到物理学领域，并被成功应用在量子多体等问题的研究中。文章简要综述了近年来张量网络和神经网络在凝聚态物理和统计物理学的应用，并讨论了两者的相互交叉和结合。

关键词：张量网络，神经网络，数值重正化群，交融
张静谢志远 | 作者
中国物理学会期刊网 | 来源

1.引言

张量重正化群是近年来发展起来的一类有效的量子多体计算方法[1]，在凝聚态物理和统计物理学诸多领域，都已经得到成功的应用。基于经典配分函数和量子波函数的张量网络表示，将物理可观测量的求解转化为对一个张量网络的求和，最终的求和主要是借助重正化群的思想进行处理。以正方晶格为例，如图1(a)所示，对于任意一个只具有最近邻相互作用的经典统计模型，其配分函数都可以严格写成一个张量网络求和的形式[2]，即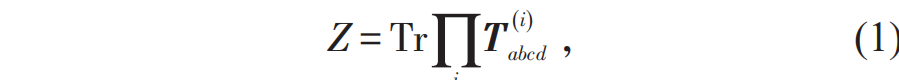其中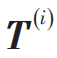代表定义在格点 i 上的张量，由温度和哈密顿量所决定，下标 a，b，c，d 分别代表局域张量的4个指标，Tr 代表对所有的指标进行求和。因此，通过对(1)式右侧求和，就能给出自由能和所有力学统计量。相应的，如图1(b)所示，对于一大类低纠缠量子态[3]，给定基矢量的叠加系数也可以表示为一个张量网络求和的形式，即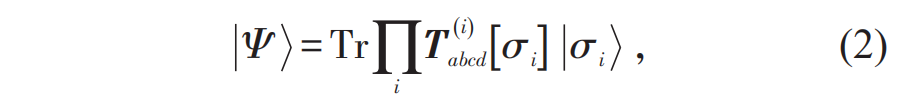其中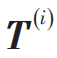仍代表定义在格点 i 上的张量，下标被称为虚拟指标。相对于(1)式，这里的T还有一个表征物理构型的指标 σi，对于1/2自旋系统，σi就代表和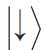两种构型。Tr代表同时对所有的虚拟指标和物理构型进行求和。张量网络的两个典型应用场景，就是利用(1)式来求解配分函数，利用(2)式来近似表示给定量子格点模型的基态和低能激发态波函数。
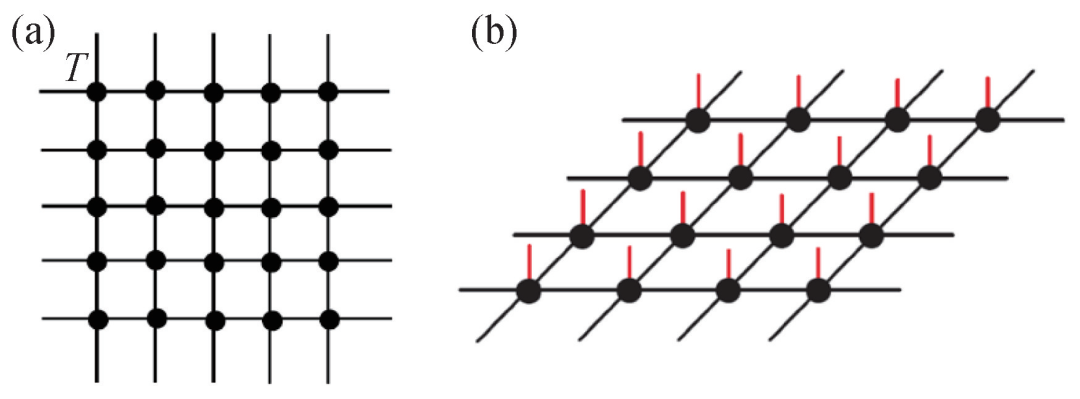图1 (a)配分函数的张量网络表示；(b)量子波函数的张量网络表示。在两图中，黑色点都代表局域张量，黑色线代表要求和掉的虚拟指标，求和之后，(a)图代表一个标量，即配分函数，(b)图代表一个矢量，即态矢量

本文涉及的神经网络特指人工神经网络，它是当前深度学习的主要实现方式和组成部分，在很多情况下已经成为深度学习的代名词[4]。虽然神经网络的早期发展受到了神经科学的启发，目的也多在模拟生物计算，但现代神经网络已经基本脱离生物学，更多地受到来自数学和工程学的指引，其成功应用已经突破了生物和计算机学科，受到数学、物理学、化学、材料科学、医学等领域的广泛关注。
本文将首先简要综述张量网络和神经网络在物理学科中的应用，讨论范围主要局限在统计物理和凝聚态多体物理领域，而后讨论两者的相似性、正在发生和可能发生的相互结合。

2.张量网络的应用

2.1 张量网络在统计物理学中的应用
(1)式是一个多重求和问题，这里的求和量是局域自由度，一般情况下无法做到严格求解，但可以借助重正化群的思想，发展粗粒化或者转移矩阵的方法进行有效近似。举例而言，在高阶张量重正化群中[5,6]，自由能 F 和局域物理量统计值 O(如能量密度、磁化密度等)，可以紧凑地表示为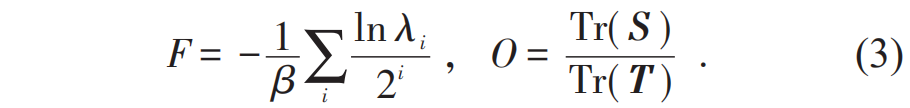这里 i 代表粗粒化的步数，λi 代表在第 i 步粗粒化中从局域张量提取的归一化系数，T 代表粗粒化完成之后所形成的局域张量，S 代表此时含有统计量 O 信息的杂质点张量。原始尺度上的 T 和 S 都可以根据模型直接写出，统计量的计算相当于在研究它们随重正化群流的演化过程。
由于可以直接处理热力学极限，张量网络相当于提供了一种没有尺寸效应的研究手段，因此很快在经典统计模型中取得成功的应用。它不仅可以用于二维统计模型，比如伊辛(Ising)模型的铁磁相变[7]，反铁磁波茨(Potts)模型中的熵致相变与部分序[8]，时钟(Clock)模型中的 KT 相变[9]等，也可以被推广到三维和四维统计模型的相变研究中[5,10]，成为研究高维格点统计模型的有效手段。除了离散自由度，借助一些可控的近似，如贝塞尔展开等，张量网络还可以有效研究连续自由度模型，如经典XY模型中的KT相变[11]。除了通过计算局域统计量，张量网络还可以通过其他方式来分析临界行为，如局域张量在重正化群流中的不动点分析[12]，高阶矩与 Binder 比值[13]，复数域的 Fisher 零点和杨—李(Yang—Lee)零点分析等[14]。
在通常的经典统计模型中，(1)式中的张量 T 是具有平移不变性的，即存在一个有限的元胞，在元胞内部T是依赖于格点的，整个系统是由该元胞进行周期性平移得到，因此张量网络可以直接处理热力学极限。但对于没有平移不变性的系统，则需要牺牲掉平移不变性，处理有限晶格系统，张量网络在这方面也有成功的应用，如Edward—Anderson 模型和 Biroli—Mezard 模型等经典自旋玻璃系统[15]。
张量网络的求和是张量重正化群的核心内容之一，不仅经典模型需要求和网络，量子格点模型的物理量和波函数的精确求解，也都需要求和网络。物理学家基于重正化群的思想发展了很多种方法进行网络求和，感兴趣的读者可以参考文献[1，3，16]，在这里不再赘述。

2.2 张量网络在量子格点模型中的应用
(2)式代表的量子态，被称为投影纠缠对态(projected entangled pair state，PEPS)[17]，它满足纠缠熵的面积定律[18]，是一类最早被广泛应用的张量网络态。不同张量网络对量子态的表达能力，决定于其对纠缠熵的刻画能力。一般来说，矩阵乘积态和树形张量网络态满足一维面积律，PEPS和它的投影纠缠单形态推广[19]，以及二维多尺度纠缠重正化拟设(multi-scale entanglement renormalization ansatz，MERA)[20]，满足二维面积律。还有一些特殊的张量网络态，可以刻画超越对应维度下面积律的纠缠熵行为，如一维MERA、二维带有分支结构的MERA[21]，具有长程关联的关联乘积态[22]等。
使用张量网络态来研究量子模型，就需要选取具有合适表达能力的波函数拟设，比如具有局域相互作用和有限基态简并度的二维量子自旋模型，对于有能隙系统，人们期望其基态是满足面积律的，因此就可以选择满足二维面积律的波函数拟设；对于无能隙系统，其基态会超越面积律，可根据计算资源选取满足或者超越二维面积律的拟设。除了少数系统比较清楚以外，关于纠缠熵的一般性讨论，目前还是一个开放性课题，具体可以参考文献[18]。
张量网络态最重要的应用场景之一，是近似一个给定格点模型的基态波函数。一般地，只要相互作用是实空间局域的，总可以使用张量网络态来逼近一个有能隙系统的基态。通过虚时演化和能量优化，它最初被应用在无阻挫自旋系统[23,24]，而后又被推广至强阻挫自旋系统[19,25,26]。这方面有价值的工作非常多，在此不能作逐一说明。值得一提的是，有一个不同但相关的研究方向，即不从具体哈密顿量出发，而是用张量网络态来构造物理上感兴趣的量子态，如对称保护态和拓扑相，从而研究这些态和对应哈密顿系统的新奇性质，这个方向上有很多有趣的工作[27,28]。如果假设系统的低能激发态也满足面积律，则还可以在得到基态波函数之后，采用单模近似的思想，使用基态的局域扰动来构造基态的正交空间，在该正交空间求解使能量极小的量子态，从而得到该系统的低能单粒子激发态[29]。
在张量网络框架下，可以非常直观地理解d维量子模型和d+1维经典模型求解的等价性，配分函数可以表示成为 d 维转移矩阵的幂次求迹。因此，如果将虚时演化方法在有限温度截止，则可以通过求和一个单方向有限的张量网络来研究量子系统的热力学性质[30]。不仅如此，由于具有相对低的复杂度和相对成熟的计算手段，矩阵乘积态和树形张量网络态，还被成功用于其他较为棘手的应用场景中，如多体局域化[31]、部分子(parton)表示[32]和开放系统动力学[33]等。
对于自旋系统，(2)式中通常对局域张量并无约束。对于玻色子系统[34]，正则系综通常会对网络作一个全局约束或集团约束，比如粒子数守恒或硬核约束，这些约束通常可以约化为局域张量的某种对称性，比如U(1)对称性，这等价于要求自旋系统处于某一个自旋分量的子空间。对于费米子系统，为了刻画粒子的反对易关系，需要对局域张量引入合适的与下标相对应的Grassmann数，使得在交换求和顺序时自动计入Grassmann代数[35]。一种简单而等价的做法是使用具有Z2对称性的局域张量，并在所有连线相交的地方引入特定的交叉规则，即两条交叉线同时具有奇宇称时产生一个负号[36]。进一步，借助对称化张量，张量网络态还可以有效推广至任意子(anyon)系统[37]。
张量网络的一个重要参数，就是下标的最大取值，即保留状态数D，它控制着波函数中的变分参数个数和表示精度。通常来讲，如果优化算法足够好，D越大则波函数表示越精确。因此，在实际计算中，一个重要的问题是如何能够在计算资源有限的情况下，尽可能地增大有效的保留状态数D。现有的解决思路主要有三种。一种是将较大D 的波函数近似成为较小D 的波函数的线性叠加，这种思路可以扩展至Krylov子空间方法的张量网络态实现，进而实现低能本征态[38]和动力学关联函数[39,40]的有效求解。由于这些工作需要计算两个态的内积，因此现有的工作都是处理有限系统。另一种是嵌套张量网络方法[41]，即通过改变张量网络的求和顺序，将期望值的求解转化为求和一个具有嵌套结构的单层张量网络，从而降低计算复杂度随D 的标度，它可以直接处理热力学极限[42,43]。还有一类解决方法，就是将蒙特卡罗抽样和张量网络表示相结合，用抽样求和来近似对物理构型或虚拟自由度的直接求和[44,45]，它便于对有限系统进行并行计算。这些方法可以有效提高保留状态数，尤其对于能隙很小的系统来说，可能是非常重要的。

2.3 张量网络在其他相关领域的应用
张量网络在其他领域也有成功的应用。在格点规范场理论中，配分函数也可以紧凑地写成张量网络求和的形式，因此可以很方便地使用张量重正化群进行数值研究[46,47]。比如在三维的U(1)规范场模型中，对应的张量网络具有双子格结构，如图2所示，在所有的正方形中心定义有一个四阶张量B (红色)，在所有的键中心定义有一个四阶张量 A (蓝色)，每个张量都与其周围的4个张量相连接。这个形式与经典统计模型非常类似。在最近的一些工作中，张量网络的定义空间，也被物理学家成功地从格点系统推广到连续极限，用于量子场论的研究[48]，这对非微扰量子场论方法的发展具有重要意义。如果将定义晶格推广到任意连接图，则张量网络算法还可以被有效应用到复杂网络[49]和随机量子线路[50]的研究中。在物理学之外，张量网络也有一些理论应用，比如在最近的工作中，通过将传统的金融理论模型转化为哈密顿系统，张量网络被用到投资组合优化[51]等问题的研究中。随着各个研究方向之间交流的增强，相信这种应用会越来越多。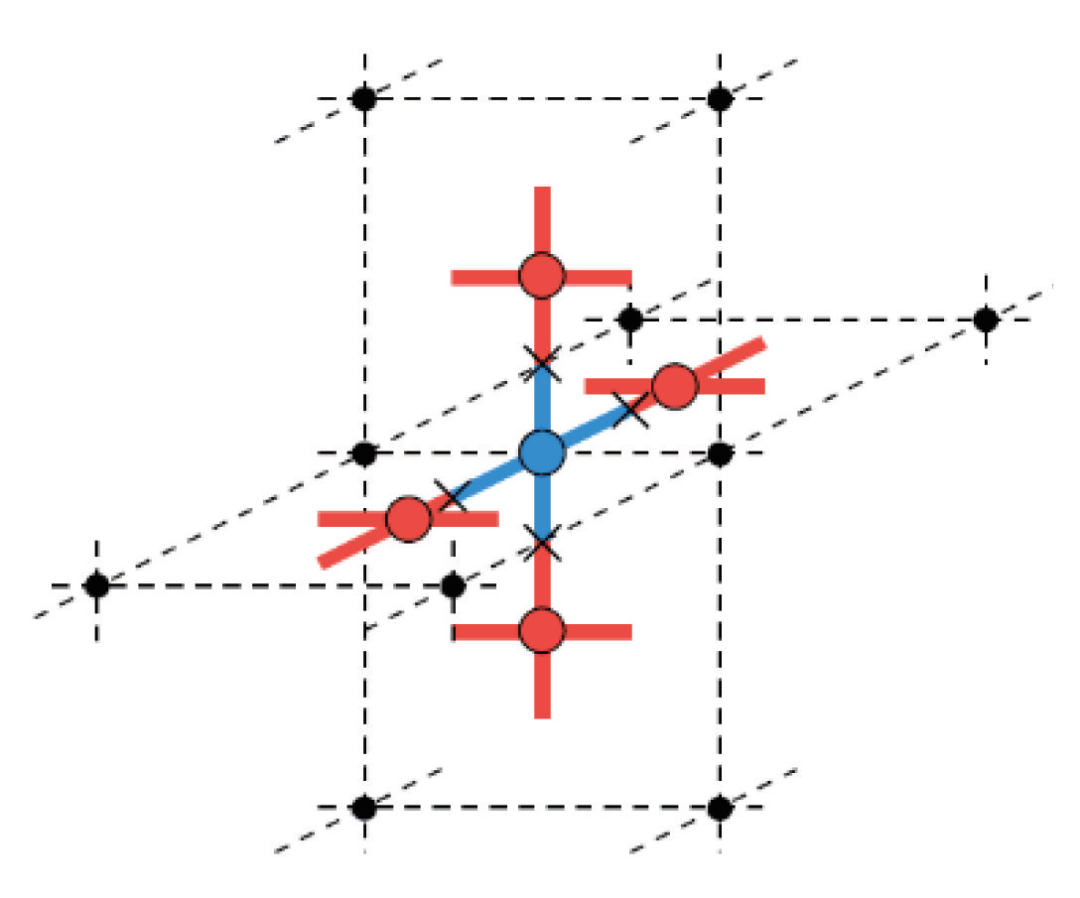图2 三维U(1)规范场模型配分函数的张量网络表示[47]。其中红色的B张量描述每一个正方形上的配分函数贡献，蓝色的A张量描述约束。黑色点与虚线代表原始晶格，× 代表求和

3.神经网络在物理学中的应用

受限玻尔兹曼机(restricted boltzmann machine，RBM)[4]，是被物理学家研究和应用最多的神经网络之一。如图3所示，它是一种特殊的只有两层神经元的浅层神经网络，其中一层是输入变量 ν，一层是需要被求和掉的隐变量 h ，其输出是一个如下精巧设计的函数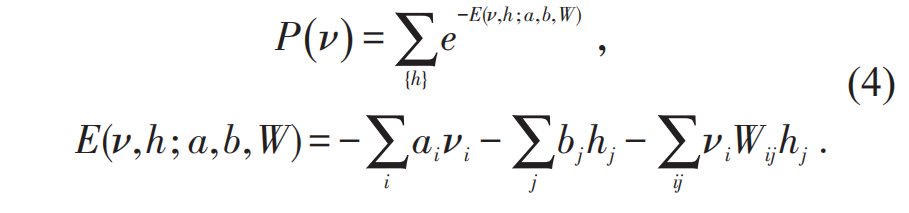：其中a，b 代表偏置参数，W 是权重参数，它们都需要通过算法学习得到。P(ν)在形式上归一化之后，可以视为一个概率函数。通过训练，该模型可以找到一组最优的参数，使得生成的概率函数P(ν)尽可能地接近真实或者期望的概率分布。由于与统计物理学理论的深刻相似性，RBM很快被物理学家所理解，用于诸如表征平衡态的统计模型[52]，量子多体系统的基态波函数[53]，混量子态的密度矩阵描述[54]，和拓扑量子态[55]等研究中。实际上，人们发现，在大多数条件下，RBM和张量网络态可以相互转化[56]，而且跟关联乘积态波函数存在非常强的联系[57]，这跟文献[58]中存在长程连接的RBM表示可以刻画体积率的纠缠熵，以及文献[59]中RBM可以探测到贝尔非局域性的结论，是相吻合的。
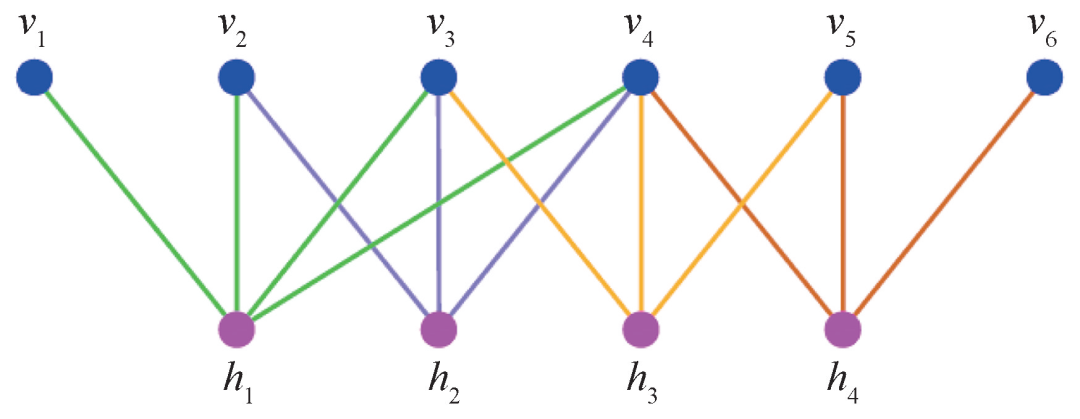图3 受限玻尔兹曼机的示意性表示[56]。隐变量h通常取离散的值，被求和掉之后，结果是关于变量ν的一个函数值，如(4)式所表达
深度神经网络通常具有更强的表达能力和泛化能力，在计算机领域应用更为广泛。前馈神经网络[4]，又叫多层感知机，是一个典型的深度学习模型，它接收一个输入 x，给出一个输出 y ，因此在数学上，该网络实际上表达了从 x 到 y 的一个映射f。在真实的应用，如分类任务中，x 是表示为向量的一张图片，y 是代表类别的一个数字或者向量，映射 f 通常被表达为一些简单函数的复合，如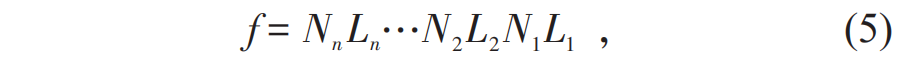这里 L 和 N 分别代表线性和非线性映射。线性映射 L 可以表示为 L(x) = Wx + b，通常 x 和 L(x) 的每一个元素都被称为一个神经元， W 代表了两层神经元之间的相互连接，被称为权重矩阵，b 是用于调整数据的偏置向量。非线性映射 N 通常由一些已知的统计函数或者具有近似阈值属性的函数所组成。W 和 b 是需要由机器学习算法来确定的参数，前者占据了神经网络中的几乎全部参数，而非线性层具有极少或者不含优化参数。这种网络结构属于有向无环图，因此称为前馈网络，如果在中间层和输出层之间加入连接，即输出对网络具有反馈，则可以扩展为循环神经网络和递归神经网络，多用于序列建模。

给定一种网络结构，学习算法的目的，在于寻找一组参数 {Wi, bi} ，使得定义在所有输入数据集上的损失函数最小，或者等价地说，使得由这些参数组成的复合函数 f 最接近于真实的映射。一方面，基于其强大的拟合能力，深度神经网络，如卷积神经网络可以被用来拟合物理数据，并以数据外推或者先验误差评估的方法来探测热力学相变和拓扑量子相变等[60]。在大多数情形，这里相变的探测其实是在确认一些已知的相变，为了真正可以预测未知的相变，神经网络也被用到了无监督学习中，如变分自编码器[61]等也可以用于热力学相变的探测。另一方面，作为表达能力更强的网络，如卷积神经网络和变分自回归网络等深度神经网络，在量子波函数表示方面更具有优势，它们可以更自然地参与到复杂的多体计算中。实际上，它们已经被成功用于统计模型的配分函数[62]和量子基态波函数[63]的求解等问题，包括阻挫自旋系统[64]和有相互作用的费米子系统[65]，引起了人们的密切关注。
更多在物理学中的应用，读者可以参考综述[66]。但需要说明的是，事实上，很多其他独立于神经网络的传统机器学习方法也可以用于探测相变，如支持向量机、扩散映射(diffusion map)、主成分分析等，也被成功地用于物理模型的相变问题研究[67]，随机森林也被用于预测具有高转变温度的高温超导材料[68]，这方面的交叉也是一个值得关注的方向。

4.张量网络和神经网络的结合

神经网络可以被应用到物理学的研究中，而同时张量网络作为一种紧凑的网络形式，自然也可以表示从输入到输出的一种映射，在机器学习领域有所作为。比如，张量网络已经被成功应用到分类任务[69,70]，生成式模型[71]，新的神经网络范式与网络压缩[72]，改良深度神经网络的优化[73]等问题的研究中。
对量子多体计算而言，交叉固然重要，但可能更重要的是能否从神经网络得到一些启发，从而改进现有计算方法，甚至发展出更高效的新的计算方法。一个很好的例子是自学习蒙特卡罗[74]，它利用局域更新方法生成的构型，拟合出一个可以进行集团更新的近似哈密顿量，进而用来加速有效抽样。思想很简单，但却能大幅度削弱临界慢化的强度。相应的，在这里也有必要考察一下张量网络和神经网络的异同。虽然两者有不同之处，比如张量网络更关心表示能够描述的纠缠熵和关联行为，而神经网络更关注对数据集的扩展能力，但两者的关联在很多工作中都被注意到[75,76]。由于求和张量网络的主要方式来源于重正化群思想，神经网络是深度学习的主要实现方式，因此两者之间的关联也反应了深度学习和重正化群两个领域之间存在的某种关联，并已经有工作试图从不同角度，通过深度学习来构建有效的重正化群变换[77,78]。在这里我们仅从网络的结构和优化方面来阐述一下两者的相似性。
简单起见，这里以二分的一维树形张量网络态为例加以说明。如图4(a)所示，假设我们已经将哈密顿量或者某个转移矩阵表示成为一个矩阵乘积算符的形式。形式上，此时的一步重正化群变换，在数值上可以视为是在该表示的每两个相邻指标(代表物理自由度)上作用一个幺正变换，该变换提取相关自由度，扔掉无关自由度。这里的相关可以简单理解为使得整个系统能量最低的那些基矢量，重正化群变换在每一个尺度上都类似地进行，最终得到原哈密顿量H 的有效低维表示H′。等价来说，如图4(a)所示的树形结构，恰好给定了原哈密顿量的最低能级本征态的张量网络表示。从优化角度来看，这里数值计算的目的是要找到合适的重正化群变换，使得到的有效H′ 和原来H 的最低能级尽可能接近。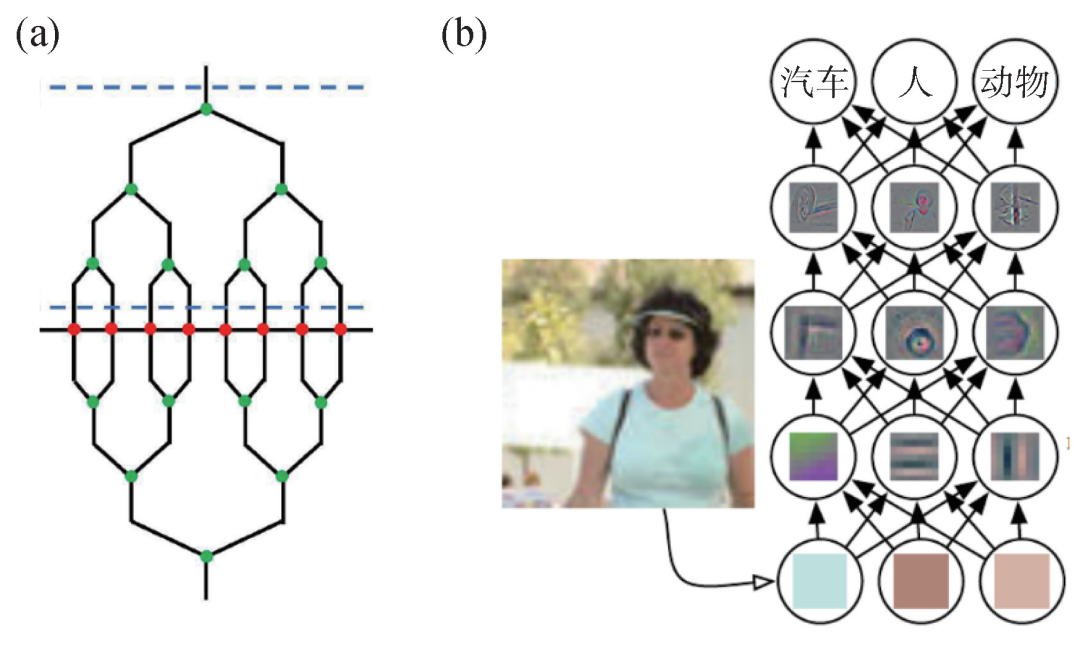

图4 (a)一维二分树形张量网络的结构与重正化群示意流程。这里红点所在的四阶张量一起构成了哈密顿量(或转移矩阵)H的矩阵乘积算符表示，绿点所在的三阶张量代表每一个尺度上所进行的局域重正化群变换，通常是一个幺正变换；(b)前馈神经网络的一个示意图[4]。这里作为分类器使用，即在底层神经层输入一个图片，经过特征提取与抽象，最终在顶层神经层输出一个类别。每一层神经元都可视为是输入图片的不同级别的表示

深度学习是一种表示性学习，即如果将它的每一层神经元视为对输入数据的不同级别的表示，则它不但要学习(5)式所表达的映射，还要学习这些表示本身。深度神经网络的不同层之间的映射，可以视为是从简单的低级别表示抽象出复杂的高级别表示，这些特征的提取和抽象，形成了与重正化群中的尺度相类似的层次结构。如图4(b)所示，在前馈网络里输入一张图片(也就是一些像素分布)，经过第一层网络的映射和抽象，在第一个隐藏层就得到了图片的最低级表示，如边缘特征；在此基础之上，经过第二层的映射和抽象，第二个隐藏层就可以得到次低级表示，如角和轮廓特征。依次类推，经过更深层的网络映射，就可以得到更高级别的抽象，如某个物理部分等，最终在输出层得到最高级别的抽象表示，如输入图像的标签(在本例就是一个人)。对于分类器而言，优化的目的是要找到合适的网络映射，使得输出的标签尽可能地接近真实情形。
由此可以看到，张量网络和神经网络的确存在一些相似之处。从输入与处理对象来看，哈密顿量、转移矩阵和波函数等，可以对应于神经网络的图片集和序列集；从计算过程来看，标度变换对应于特征的抽象与提取，前者的扫描或优化，在后者被称为训练或学习；从表象来看，有效的张量网络表示对应于特征映射或者神经层；从优化目标来看，能量本征值，配分函数(自由能)，对应于损失函数(如交叉熵)。
更细致的研究表明，两者的优化方式也有很多相似之处。神经网络中参数的优化策略，占据主流的是基于反向传播算法的梯度优化方式，对于给定的批次(batch)输入而言，这是对网络参量进行全局优化。在最近的工作中[79]，我们证明了在张量网络框架下，这种优化方式等价于张量网络的一种高效全局优化方式，即二次重正化群[24]：神经网络中的梯度对应于张量网络中的环境概念，而求解梯度的反向传播算法对应于求解环境的后向迭代步骤。该等价性在数值上得到了验证，并促使我们将神经网络的优化技术，如自动微分，嵌入到张量网络的优化中，用于实现并改良原有重正化群算法。考虑到这些相似性，以及导数在波函数优化中的成功应用[45,80]，可以预期，类似自动微分这种在神经网络中被广泛采用的优化技术，未来将会在张量网络的计算中占据重要一席，而张量网络发展出的一些概念和方法，如正则化表示[3]等，也有可能在神经网络的优化中发挥重要作用。

5.总结与展望

张量网络和神经网络是两个相对年轻但发展非常迅速的领域，它们的交叉也是一个非常活跃的研究领域，限于篇幅和个人视野，即使局限在统计物理和凝聚态物理领域，本文所提及的研究课题也只能覆盖其中一部分。但可以预期的有两点：(1)两个领域的交叉会催生出与其他领域的更多交叉[81]，产生更多新的思想和方法；(2)这些理论方法会逐渐渗透到实验领域[82,83]，吸引越来越多实验物理学家的关注和参与。对于有兴趣的读者，笔者强烈建议阅读本文的参考文献，它们已经尽可能被安排在最合适的地方。笔者一个主要的研究方向是量子多体计算方法，与这个交叉领域密切相关，希望本文的概述可以吸引更多新生力量加入进来，不断壮大国内多体计算的研究队伍。

致谢感谢物理所向涛课题组成员，以及赵汇海、刘玉志、王磊、张潘、李伟、王锐、邹海源等合作者的讨论。
参考资料
[1] 乐宏昊，谢志远. 物理，2017，46(7)：424；刘耘婧，陈斌斌，李伟.物理，2017，46(7)：430；娄捷. 物理，2017，46(7)：439[2] Zhao H H，Xie Z Y，Chen Q N et al. Phys. Rev. B，2010，81：174411[3] Orus R. Annals of Physics，2014，349：117[4] Goodfellow I，Bengio Y，Courville A. Deep Learning . MIT press，2016[5] Xie Z Y，Chen J，Qin M P et al. Phys. Rev. B，2012，86：045139[6] Zhao H H，Xie Z Y，Xiang T et al. Phys. Rev. B，2016，93：125115[7] Levin M，Nave C P. Phys. Rev. Lett.，2007，99：120601[8] Chen Q N，Qin M P，Chen J et al. Phys. Rev. Lett.，2011，107：165701[9] Li Z Q，Yang L P，Xie Z Y et al. Phys. Rev. E，2020，101：060105[10] Akiyama S，Kuramashi Y，Yamashita T et al. Phys. Rev. D，2019，100：054510[11] Yu J F，Xie Z Y，Meurice Y et al. Phys. Rev. E，2014，89：013308[12] Meurice Y. Phys. Rev. B，2013，87：064422；Gu Z C，Wen X G. Phys. Rev. B，2009，80：155131[13] Morita S，Kawashima N. Computer Physics Communications，2019，236：65[14] Denbleyker A，Liu Y Z，Meurice Y et al. Phys. Rev. D，2014，89：016008；Saez A G，Wei T C. Phys. Rev. B，2015，92：125132[15] Wang C，Qin S M，Zhou H J. Phys. Rev. B，2014，90：174201；Yoshiyama K，Hukushima K. J. Phys. Soc. Jpn.，2020，89：104003[16] Ran S J，Tirrito E，Peng C et al. Tensor Network Contractions.Springer Open，2020[17] Verstraete F，Cirac J I. 2004，arXiv：0407066[18] Eisert J，Cramer M，Plenio M B. Rev. Mod. Phys.，2010，82：277[19] Xie Z Y，Chen J，Yu J F et al. Phys. Rev. X，2014，4：011025[20] Vidal G. Phys. Rev. Lett.，2008，101：110501[21] Evenbly G，Vidal G. Phys. Rev. Lett.，2014，112：240502[22] Changlani H J，Kinder J M，Umrigar C J et al. Phys. Rev. B，2009，80：245116[23] Jordan J，Orus R，Vidal G et al. Phys. Rev. Lett.，2008，101：250602[24] Xie Z Y，Jiang H C，Chen Q N et al. Phys. Rev. Lett.，2009，103：160601[25] Wang L，Gu Z C，Verstraete F et al. Phys. Rev. B，2016，94：075143；Liu W Y，Dong S，Wang C et al. Phys. Rev. B，2018，98：241109[26] Corboz P，Mila F. Phys. Rev. B，2013，87：115144[27] Chen X，Gu Z C，Wen X G. Phys. Rev. B，2011，83：035107；Schuch N，Garcia D P，Cirac I. Phys. Rev. B，2011，84：165139[28] Schuch N，Cirac J I，Perez- Garcia D. Ann. Phys.，2010，325：2153；Xu W T，Zhang Q，Zhang G M. Phys. Rev. Lett.，2020，124：130603[29] Haegeman J，Osborne T J，Verstraete F. Phys. Rev. B，2013，88：075133；Vanderstraeten L，Marien M，Verstraete F et al. Phys. Rev. B，2015，92：201111[30] Li W，Ran S J，Gong S S et al. Phys. Rev. Lett.，2011，106：127202；Chen B B，Chen L，Chen Zet al. Phys. Rev. X，2018， 8：031082[31] Yu X，Pekker D，Clark B K. Phys. Rev. Lett., 2017，118：017201[32] Wu Y H，Wang L，Tu H H. Phys. Rev. Lett., 2020，124：246401；Jin H K，Tu H H，Zhou Y. Phys. Rev. B，2020，101：165135[33] Schroder F，Turban D，Musser A J et al. Nat. Commu., 2019，10：1062[34] Jordan J，Orus R，Vidal G. Phys. Rev. B，2009，79：174515[35] Gu Z C，Verstraete F，Wen X G. 2010，arXiv：1004.2563；Gu Z C. Phys. Rev. B，2013，88：115139[36] Kraus C V，Schuch N，Verstraete F et al. Phys. Rev. A，2010，81：052338；Corboz P，Orus R，Bauer B et al. Phys. Rev. B，2010，81：165104[37] Bridgeman J C，Bartlett S D，Doherty A. Phys. Rev. B，2017，96：245122；Ayeni B M. Studies of braided non-Abelian anyons using anyonic tensor networks. PhD thesis, Macquarie University，2017[38] Huang R Z，Liao H J，Liu Z Y et al. Chin. Phys. B，2018，27：070501[39] Xie H D，Huang R Z，Han X J et al. Phys. Rev. B，2018，97：075111[40] Holzner A，Weichselbaum A，McCulloch I P et al. Phys. Rev. B，2011，83：195115；Dargel P E，Wollert A et al. Phys. Rev. B，2012，85：205119[41] Xie Z Y，Liao H J，Huang R Z et al. Phys. Rev. B，2017，96：045128[42] Liao H J，Xie Z Y，Chen J et al. Phys. Rev. Lett.，2017，118：137202[43] Lee C Y，Normand B，Kao Y J. Phys. Rev. B，2018，98：224414；Haghshenas R，Gong S S，Sheng D N. Phys. Rev. B，2019，99：174423[44] Wang L，Pizorn I，Verstraete F. Phys. Rev. B，2011，83：134421；Zhao H H，Ido K，Morita S et al. Phys. Rev. B，2017，96：085103[45] Liu W Y，Dong S J，Han Y J et al. Phys. Rev. B，2017，95：195154；Dong S J，Wang C，Han Y J et al. Phys. Rev. B，2019，99：195153[46] Liu Y Z，Meurice Y，Qin M P et al. Phys. Rev. D，2013，88：056005[47] Meurice Y，Sakai R，Yockey J U. 2020，arXiv：2010.06539[48] Verstraete F，Cirac J I. Phys. Rev. Lett.，2010，104：190405；Tilloy A，Cirac J I. Phys. Rev. X，2019，9：021040；Haghshenas R，Cui Z H，Chan G K L. 2020，arXiv：2008.10566[49] Pan F，Zhou P，Li S et al. Phys. Rev. Lett.，2020，125：060503；Kourtis S，Chamon C，Mucciolo E R et al. SciPost Phys.，2019， 7：060[50] Markov I L，Shi Y. SIAM J. Comput.，2008，38：963[51]Mugel S，Kuchkovsky C，Samuel E S et al. 2020，arXiv：2007.00017[52] Torlai G，Melko R G. Phys. Rev. B，2016，94：165134[53] Carleo G，Troyer M. Science，2017，355：602；Nomura Y，Imada M. 2020，arXiv：2005.14142[54] Torlai G，Melko R G. Phys. Rev. Lett.，2018，120：240503[55] Deng D L，Li X P，Sarma S D. Phys. Rev. B，2017，96：195145[56] Chen J，Cheng S，Xie H D et al. Phys. Rev. B，2018，97：085104[57] Clark S R. J. Phys. A: Math. Theor., 2018，51：135301[58] Deng D L，Li X P，Sarma S D. Phys. Rev. X，2017，7：021021[59] Deng D L. Phys. Rev. Lett., 2018，120：240402[60] Carrasquilla J，Melko R G. Nat. Phys.，2017，13：431；Nieuwenburg E P L，Liu Y H，Huber S D. Nat. Phys.，2017，13：435[61] Wetzel S J. Phys. Rev. E，2017，96：022140[62] Wu D，Wang L，Zhang P. Phys. Rev. Lett.，2019，122：080602[63] Sharir O，Levine Y，Wies N et al. Phys. Rev. Lett.，2020，124：020503[64] Cai Z，Liu J G. Phys. Rev. B，2018，97：035116；Liang X，Liu WY，Lin P Z et al. Phys. Rev. B，2018，98：104426[65] Pfau D，Spencer J S，Matthews A. Phys. Rev. Research，2020，2：033429 ；Hermann J，Schatzle Z，Noe F. Nature Chemistry，2020，12：891[66] Carleo G，Cirac I，Cranmer K et al. Rev. Mod. Phys.，2019，91：045002；Bedolla E，Padierna L C，Preigo R. J. Phys.：Condens. Matter.，2021，33：053001[67] Greitemann J，Liu K，Pollet L. Phys. Rev. B，2019，99：060404；Lidiak A，Gong Z. Phys. Rev. Lett.，2020，125：225701；Wang C，Zhai H. Front. Phys.，2018，13：130507[68] Staev V，Oses C，Kusne A G et al. npj Computational Materials，2018，4：29[69] Novikov A，Trofimov M，Oseledets I. ICLR 2017，arXiv：1605.03795；Stoudenmire E，Schwab D J. Adv. NIPS，2016，29：4799[70] Liu D，Ran S J，Wittek P et al. New J. Phys.，2019，21：073059；Cheng S，Wang L，Zhang P. 2020，arXiv：2009.09932[71] Han Z Y，Wang J，Fan H et al. Phys. Rev. X，2018，8：031012；Cheng S，Wang L，Xiang T et al. Phys. Rev. B，2019，99：155131[72] Gao Z F，Cheng S，He R Q. Phys. Res. Research，2020，2：023300；Sun X，Gao Z F，Lu Z Y et al. TASLP，2020，3030495，arXiv：2010.04950[73] Sun Z Z，Ran S J，Su G. Phys. Rev. E，2020，102：012152[74] Liu J W，Qi Y，Meng Z Y et al. Phys. Rev. B，2017，95：041101；Huang L，Wang L. Phys. Rev. B，2017，95：035105[75] Saremi S，Sejnowski T J. PNAS，2013，110：3071；Beny C. 2013，arXiv：1301.3124[76] Lin H W，Tegmark M，Rolnick D. J. Stat. Phys.，2017，168：1223；Mehta P，Schwab D J. 2014，arXiv：1410.3831；2016，arXiv：1609.0354[77] Janusz M K，Ringel Z. Nat. Phys.，2018，14：578[78] Li S H，Wang L. Phys. Rev. Lett.，2018，121：260601[79] Chen B B，Gao Y，Guo Y B et al. Phys. Rev. B，2020，101：220409[80] Liao H J，Liu J G，Wang L et al. Phys. Rev. X，2019，9：031041[81] Liu J G，Mao L，Zhang P et al. 2019，arXiv：1912.11381[82] Yu S，Gao Y，Chen B B et al. 2020，arXiv：2011.12282[83] Zuo Y，Li B，Zhao Y et al. Optica，2019，6：1132

（可上下滑动浏览）

复杂科学最新论文

集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅：