Nature 通讯:渗流理论让网络可靠又高效

导语
交通拥堵严重影响人们的出行体验,准确识别路网瓶颈并对指施加保护可以大大提高交通系统的运行效率。近日,澳洲莫纳什大学的研究团队在 Nature Communications上发表的文章提出了一种基于渗流理论的异质需求流网络瓶颈路段识别方法和网络可靠性衡量指标。该理论框架可以适用于其他的基础设施网络中,多学科交叉的研究方法这为网络优化提供了新视角。 胡一冰 | 作者邓一雪 | 编辑
胡一冰 | 作者邓一雪 | 编辑
 论文题目:
论文题目:
Percolation of heterogeneous flows uncovers the bottlenecks of infrastructure networks
论文地址:https://www.nature.com/articles/s41467-021-21483-y
1. 交通网络中的渗流现象
渗流理论(Percolation theory)最早应用于数学和统计物理中,它常常被用来描述网络系统的结构、功能和韧性,通过逐一从网络中删除边的过滤模型来模拟元素故障或扰动传播。这类故障或扰动的影响常借助“巨片”(giant component)大小来衡量。 在现实基础设施网络中,渗流现象也普遍存在。例如交通网络中的持续拥堵会导致路段行驶速度大幅降低,出行者们只能“龟速”行进。倘若用参数![]() 来反映路段
来反映路段![]() 的运行水平,交通网络G上渗流阈值为
的运行水平,交通网络G上渗流阈值为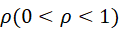 。当
。当 时,可以认为该路段运行效率过低,低于渗流阈值,从而导致该路段失效,故可从网络G上移除,重新得到新的子网络
时,可以认为该路段运行效率过低,低于渗流阈值,从而导致该路段失效,故可从网络G上移除,重新得到新的子网络![]() 。 特别需要注意的是,存在临界渗流阈值
。 特别需要注意的是,存在临界渗流阈值![]() (critical percolation threshold)使得连通的巨片迅速碎片化成多个小的集团,全网的通达程度大大降低。试想在交通网络达到其临界渗流阈值后,原本完好的路网因拥堵而导致多条路段几近失效,从而连通多个起点(origin)和终点(destination)之间的路径被堵塞。这样存在需求流动的点对也称之为“OD对”(origin-destination pair),其上的需求量称为OD量。若交通路网堵塞,将有大量的OD对上的出行需求无法得到满足,路网的可靠性堪忧。
(critical percolation threshold)使得连通的巨片迅速碎片化成多个小的集团,全网的通达程度大大降低。试想在交通网络达到其临界渗流阈值后,原本完好的路网因拥堵而导致多条路段几近失效,从而连通多个起点(origin)和终点(destination)之间的路径被堵塞。这样存在需求流动的点对也称之为“OD对”(origin-destination pair),其上的需求量称为OD量。若交通路网堵塞,将有大量的OD对上的出行需求无法得到满足,路网的可靠性堪忧。 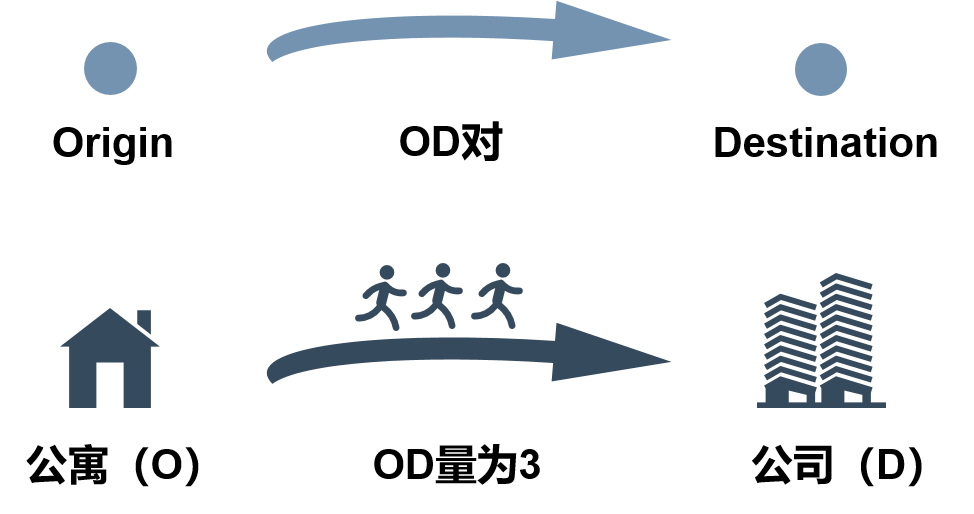 图1:OD和OD量示意图。从公寓到公司上班,公寓和公司可构成一组OD对。如果有3个人从该公寓到该公司上班,则“公寓-公司”OD对的OD量(出行需求量)为3。
图1:OD和OD量示意图。从公寓到公司上班,公寓和公司可构成一组OD对。如果有3个人从该公寓到该公司上班,则“公寓-公司”OD对的OD量(出行需求量)为3。
2. 从渗流角度诠释交通网络可靠性
相较以往的研究,该文章基于渗流理论引入可体现路网服务质量的指标UD(unaffected demand),提出了新的交通网络可靠性指标α。下面通过一个例子,方便读者理解结合渗流理论和出行需求的交通网络可靠性量化方法(见图2 )。 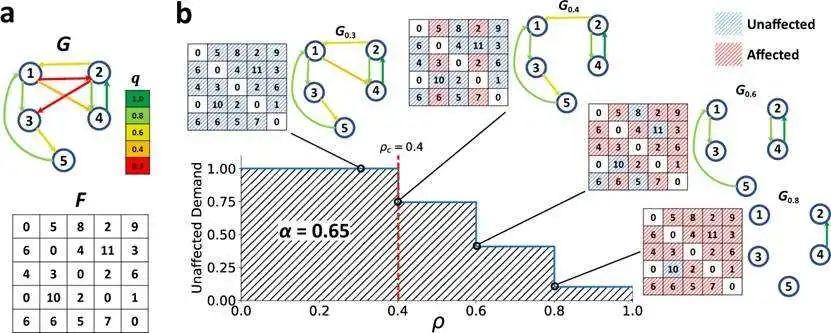 图2:基于渗流理论的交通网络可靠性量化示意图 在图2a中小网络G内存在5个节点,两两之间均可连通。下方F为图G中各OD需求矩阵,矩阵内
图2:基于渗流理论的交通网络可靠性量化示意图 在图2a中小网络G内存在5个节点,两两之间均可连通。下方F为图G中各OD需求矩阵,矩阵内![]() 表示起点i到终点j之间的需求,所有需求之和为100。例如图1中共有19组OD对,1和5上间OD量为9,2和3间OD量为3,4和1间不存在出行需求,即
表示起点i到终点j之间的需求,所有需求之和为100。例如图1中共有19组OD对,1和5上间OD量为9,2和3间OD量为3,4和1间不存在出行需求,即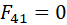 。 用来反映路段
。 用来反映路段![]() 运行水平的参数
运行水平的参数![]() 表示“实际通过速度/理想通过速度”,
表示“实际通过速度/理想通过速度”,![]() 值越大,意味着
值越大,意味着![]() 路段更为通畅。当
路段更为通畅。当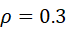 时,
时,![]() 0.3的路段即可视为失效,可从原网络中移除此路段,但此时所有OD间路径仍然可达,所有出行需求并未受到影响,此时UD=1。当
0.3的路段即可视为失效,可从原网络中移除此路段,但此时所有OD间路径仍然可达,所有出行需求并未受到影响,此时UD=1。当 时,
时,![]() 0.4的路段被删去得到
0.4的路段被删去得到![]() ,此时共有6个OD对需求受到影响(图中红色阴影),仍有70的出行量可以被满足,
,此时共有6个OD对需求受到影响(图中红色阴影),仍有70的出行量可以被满足,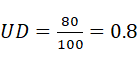 。以此类推,可以得到图1下方的坐标图,横轴为渗流阈值
。以此类推,可以得到图1下方的坐标图,横轴为渗流阈值![]() ,纵轴为不受影响的需求总量。蓝线UD所围成的阴影面积即为网络的可靠性α。
,纵轴为不受影响的需求总量。蓝线UD所围成的阴影面积即为网络的可靠性α。
3. 路段关键程度排名锁定网络瓶颈
该研究中引入路段关键性评分![]() (link criticality score)量化每条路段对网络中出行需求流动的整体影响,从而形成一套锁定交通网络瓶颈路段的框架,将其称之为CS(criticality score)法。
(link criticality score)量化每条路段对网络中出行需求流动的整体影响,从而形成一套锁定交通网络瓶颈路段的框架,将其称之为CS(criticality score)法。![]() 表示某个OD对间所有路径集合,在不同的路径中选择
表示某个OD对间所有路径集合,在不同的路径中选择![]() 值最低的路段集合。在这个特定集合内选出
值最低的路段集合。在这个特定集合内选出![]() 值最大的路段作为该条路径限制路段
值最大的路段作为该条路径限制路段![]() (limiting link)。具体
(limiting link)。具体![]() 的计算公式可写作:
的计算公式可写作: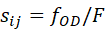 ,即所处OD的出行需求量和总需求量的比值。同样举一个例子来介绍说明CS法的求解思路(见图3)。
,即所处OD的出行需求量和总需求量的比值。同样举一个例子来介绍说明CS法的求解思路(见图3)。 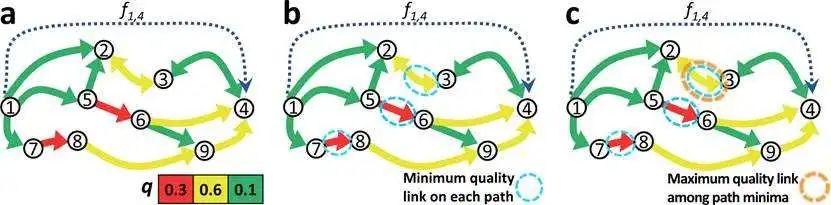 图3:CS法瓶颈路段识别示意图 图3中节点1和节点4之间存在出行需求,现共有5条路径可实现从1到4。
图3:CS法瓶颈路段识别示意图 图3中节点1和节点4之间存在出行需求,现共有5条路径可实现从1到4。![]() 值最低集合中包含
值最低集合中包含![]() 、
、![]() 和
和![]() ,在此之中由于
,在此之中由于![]() 的
的![]() 值最高。将
值最高。将![]() 和总需求量的比值加载到
和总需求量的比值加载到![]() 上,以表示路段
上,以表示路段![]() 的运行水平对网络出行需求流通的关键程度。 如果某一条路段是多个OD对间的限制路段,那么其关键性评分
的运行水平对网络出行需求流通的关键程度。 如果某一条路段是多个OD对间的限制路段,那么其关键性评分![]() 即为在关键性OD部分的得分之和。对所有路段求得关键性评分后,即可进行排名,评分最高的路段应重点施加保护。 此外,经过推导可得到网络可靠性α和各路段关键性评分
即为在关键性OD部分的得分之和。对所有路段求得关键性评分后,即可进行排名,评分最高的路段应重点施加保护。 此外,经过推导可得到网络可靠性α和各路段关键性评分![]() 、路段运行水平
、路段运行水平![]() 的关系满足:
的关系满足: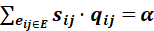 。具体推导可参照原文支撑材料。
。具体推导可参照原文支撑材料。
4. 交通瓶颈的改善与优化效果
研究者们利用澳大利亚墨尔本和布里斯班两个主要城市的公交网络相关数据分析了网络的渗流过程,并检验了上述理论方法的有效性。和以往研究采用的瓶颈识别方法相比,CS方法结果更贴合真实网络瓶颈。此外,该研究还对进行时空对比分析,如是否为工作日,是否为早晚高峰,是否处于大学城附近等等。 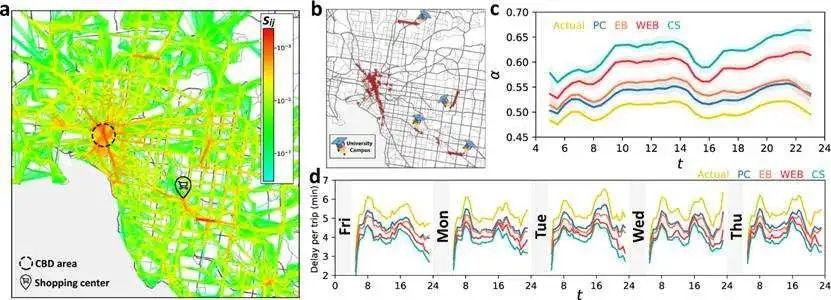 图4:CS法在真实公交网络中的应用。a为工作日期间墨尔本公交网络的关键性评分空间分布;b为工作日墨尔本公交网络的排名前100的瓶颈路段;c和d为与不同瓶颈识别方法的优化效果对比
图4:CS法在真实公交网络中的应用。a为工作日期间墨尔本公交网络的关键性评分空间分布;b为工作日墨尔本公交网络的排名前100的瓶颈路段;c和d为与不同瓶颈识别方法的优化效果对比
在模拟多种网络优化的方法之后,对于提高路面公交网络的可靠性,最有效的措施是减少公交车辆和路面状态的冲突,如实施公交信号有限或分配单独的公交车道,已达到路面运行水平尽可能![]() 靠近1。另外,该研究还验证CS法瓶颈改善后对减少人们出行时间延误的影响,优化效果明显。
靠近1。另外,该研究还验证CS法瓶颈改善后对减少人们出行时间延误的影响,优化效果明显。
5. 学科交叉迸发创新视角
该研究基于渗流理论为交通网络可靠性和缓解堵塞的研究提供了新视角。但值得注意的是,拥堵对出行者延误的直接影响不能用现有的渗流模型来研究。但这是一个有趣的问题,为未来的研究指明了一个重要的方向。 该研究的理论框架可适用于需求服务网络,包括大多数物理基础设施,需要有内部流动的需求且各OD对间需求不均匀。现实世界中基础设施网络的不断增加,本研究用新的研究途径和复杂科学理论来分析流量需求,这可以帮助人们对这类复杂系统有更深刻的理解。
网络科学新课推荐:网络动力学
集智学园特邀陈关荣、项林英、樊瑛、宣琦、李翔、史定华、李聪、荣智海、周进、王琳等网络科学专家作为导师,依托汪小帆、李翔、陈关荣的经典教材《网络科学导论》,自2月27日起开展系列上线课程,以网络动力学为主线构建网络科学知识体系。欢迎希望进入网络科学领域、提高网络分析能力、与一线专家探讨问题的朋友报名参加!

点击查看课程详情:2021重磅新课:探索网络动力学——网络科学第二期
推荐阅读
城市交通复杂系统背后的简单线性模型网络遇见大数据:在大型静态数据集中恢复动态网络元胞自动机揭示交通瘫痪成因:车多路窄惹的祸
加入集智,一起复杂!
点击“阅读原文”,追踪复杂科学顶刊论文










