由于细胞间相互作用的复杂性,理解大规模的神经元活动是困难的,在此背景下粗粒化等技术获得了广泛应用。2021年3月17日发表在 Physical Review Letters 的一篇论文,利用重整化群方法,以神经系统数据为例,探讨了大型生物系统中时空临界性与潜在的动力学变量之间的关系。
期刊来源:PRL
Latent Dynamical Variables Produce Signatures of Spatiotemporal Criticality in Large Biological Systems
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.126.118302
现代生物物理学中的一个关键问题是从由高通量实验实现的海量数据集中提取有用的知识。例如,现在可以记录数千个神经元的同一时刻下的状态或基因表达;或微生物群落中,物种的丰富度。但目前,科研人员依然难以推断并解释这么多变量的联合概率分布。解决该问题的一个有前途的解决方案是将重整化群(renormalization group,RG)框架应用于统计物理学中的粗粒度系统,以在生物数据集中找到相关特征和大规模行为。
研究人员发现,当活动变量的数量很大时,很难用它们的联合概率分布进行工作,因而需要借助粗粒来开发可解释的数据模型。科研人员已经表明,在两种不同的粗粒度方案下,一种人口活动模型(其中神经元(自旋)随机耦合到一些缓慢变化的潜在刺激或场(一定量不足以适应数据))展示了幂律尺度关系。这种关联和活动分布向非高斯固定点的流动的现象,已在小鼠海马区实验中得到证实。其他模型,例如随机连接速率网络(randomly connected rate network)或同步不规则状态下的 Brunel 神经网络(Brunel neural network),则无法重现这些结果。研究人员证明了缩放的出现需要多个与时间有关的潜伏过程,这解释了为什么先前的模型不能复制这些小鼠海马区实验数据。
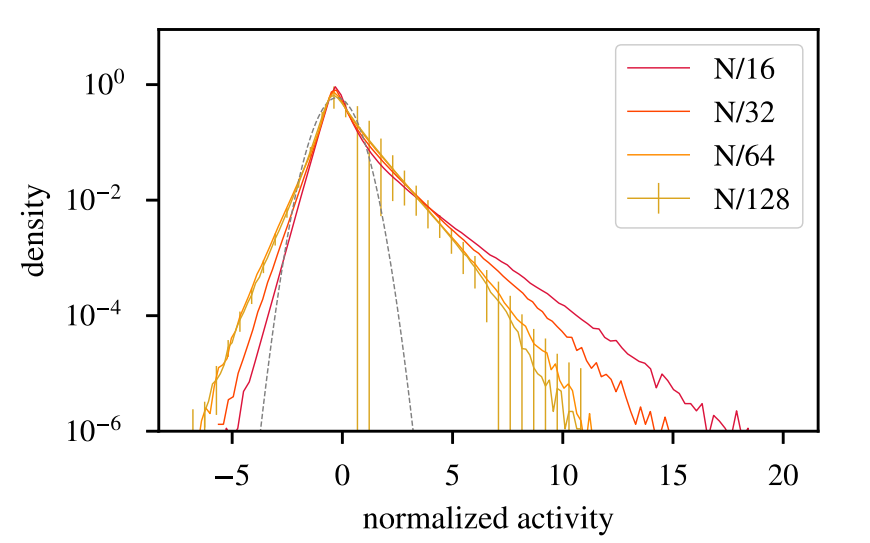
在动量空间粗粒度下保留了 k=N/16;k=N/32;k=N/64;k=N/128 模式,并显示了高斯分布(灰色虚线)以进行比较。
研究人员本次关注的粗粒度方法、尤其是动量空间分析,已被证明在区分关键模型和非关键模型方面效果显著。更重要的是,在他们的模型类别中,几乎无标度的分布必然会在重整化的情况下出现:这不需要微调,并且比例关系对于较大的系统尺寸(对于神经元数量级更高的结果)变得更加稳健。这就提出了一个问题,即是否以及何时将多元生物系统中的表观规模看成是更为传统的临界的证据,这种临界是通过内部相互作用参数的微调而出现的。
虽然这篇文章中,作者专注于神经数据,但更重要的结果是,预测本函中讨论的表观比例关系——无论它们是否应被视为临界特征——都将从任何稀疏活跃的多元系统(无论是生物系统、无生命的、社会的或人为的)中,显示由数个潜在的动力学过程驱动。
集智斑图顶刊论文速递栏目上线以来,持续收录来自Nature、Science等顶刊的最新论文,追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能,每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅:
点击“阅读原文”,追踪复杂科学顶刊论文