Nature Reviews Physics综述:网络几何

导语
网络是有限的度量空间,其距离由节点之间最短路径所定义,但这并非网络几何结构的唯一形式,网络的几何结构也可以通过隐空间、动力学过程定义。近日发表在 Nature Reviews Physics 的长文综述“Network geometry”,回顾了网络几何研究方法的核心理论和应用,并展望了未来复杂性科学研究的方向与挑战。本文是对该综述的要点简介。

郭瑞东 | 译者
刘培源 | 审校
邓一雪 | 编辑

论文题目:
Network geometry
论文地址:
https://www.nature.com/articles/s42254-020-00264-4
除了将网络定义为两点之间最短距离组成的矩阵,还可以根据网络在隐空间的几何,及网络的动力学过程来定义网络的几何结构。这三种定义是密切相关的,每一种都能够很高效地发现诸如分形、标度不变性、自相似等网络的基本特征。网络的几何结构有很多实际用途,例如理解大脑的运作、互联网中的路由。
从统计物理中,衍生出许多用于复杂网络的分析方法。进20年来,这些方法被证明能复现真实世界网络的诸多特征,也能用于量化网络的结构特征对群体和临界现象的重要性。这些方法中就包含了该综述的主题:网络几何(network geometry)。
复杂网络能够在恰当的尺度变化下,保持自相似性,这意味着网络的几何特征并不简单。最初的研究方法,多来自分形几何。该范式带来了可以将网络分为一般类(university class)的正则化方法,这些方法可用于理解网络的生成机制,及其时序演化过程。
之后,研究者发现网络的分形特征,可以在更基础的层次上,通过隐藏的双曲几何来解释。隐空间的概念自从上世纪提出后,被用做对社交网络中的的节点一致性建模。在这些模型中,节点被置于相似度空间,节点间的连边是随机的生成的,距离越近可能性越高,这意味着相似度越高的节点越容易被连接。
双曲映射成为了最常用的解释很多真实网络特征(例如网络的可传导、网络中的社团、多尺度结构)的统一框架。由于双曲几何的对称性在洛仑兹群上是同态的,双曲几何中的特征,不仅能解释网络的自相似性,还能解释网络生成过程的动力学规则。
由于上述性质,网络几何有很多实际的应用。例如在信息或疾病的传播中,引入基于交通的衡量尺度以及对应的扩散几何,能帮助解释时空演化过程的网络动力学。这为很多相关领域的新研究指明方向。
该综述原文虽然长达23页,但对网络几何的介绍仍然是概略性的,并未完全囊括。对该话题感兴趣的读者,请详细阅读该综述。下文截取原文中关键的几幅图,简要介绍网络几何的应用领域:
1. 网络正则化:三种网络压缩的方式
1. 网络正则化:三种网络压缩的方式
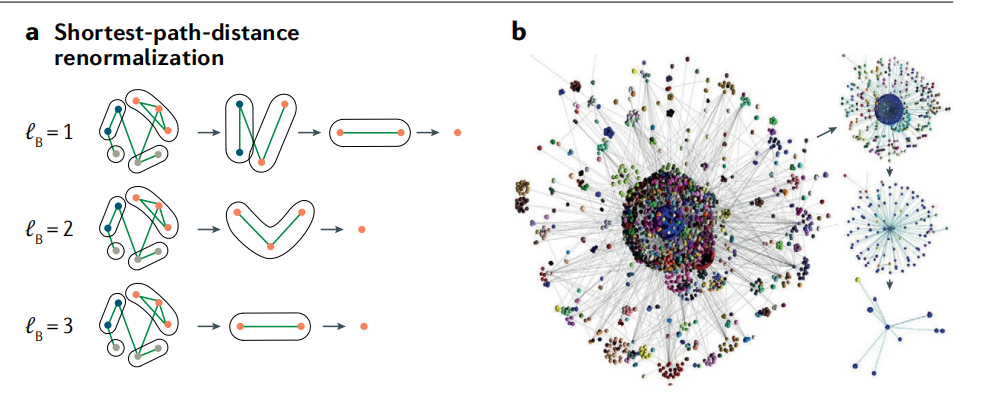
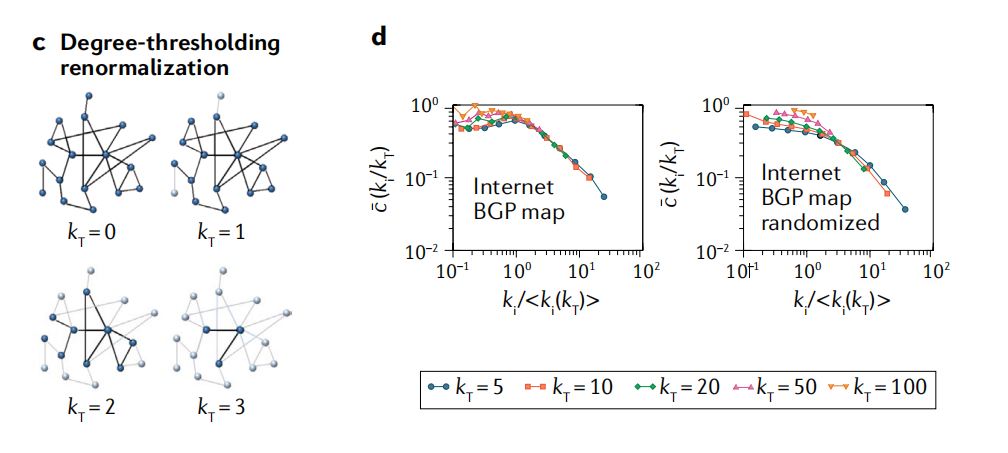
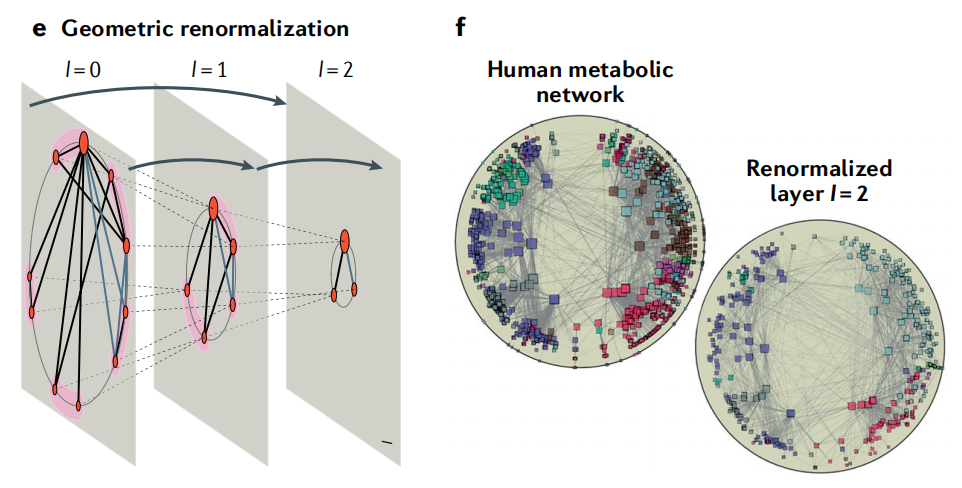 图1:三种网络压缩的方法示意图
图1:三种网络压缩的方法示意图
2. 从小世界网络到分形网络
2. 从小世界网络到分形网络
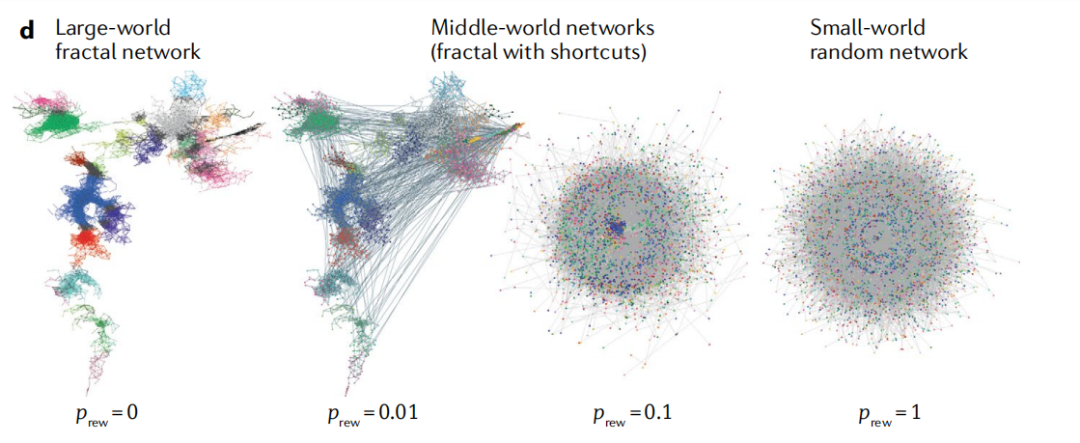
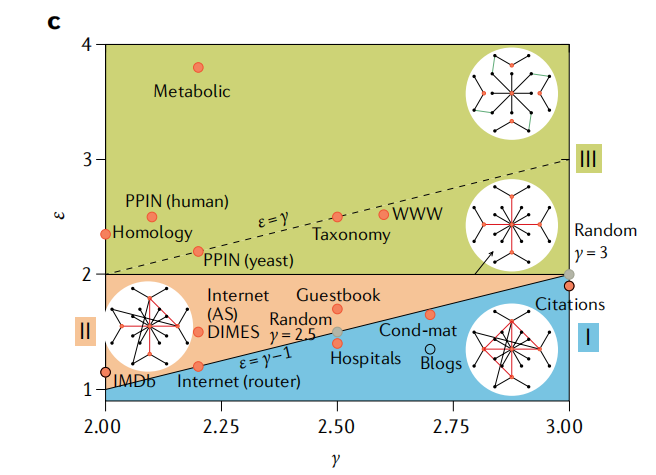 图3:不同类型网络根据几何结构可分为三类
图3:不同类型网络根据几何结构可分为三类
3. 网络正则化的过程代表了网络的时序演化
3. 网络正则化的过程代表了网络的时序演化
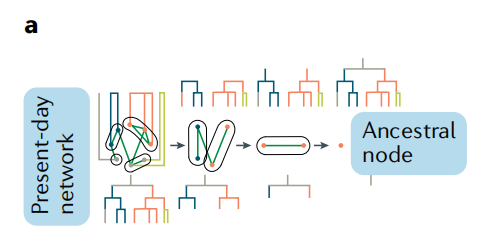 图4:对当前网络,使用最短路径正则化,可以得到更古老场景下,节点更少的网络
图4:对当前网络,使用最短路径正则化,可以得到更古老场景下,节点更少的网络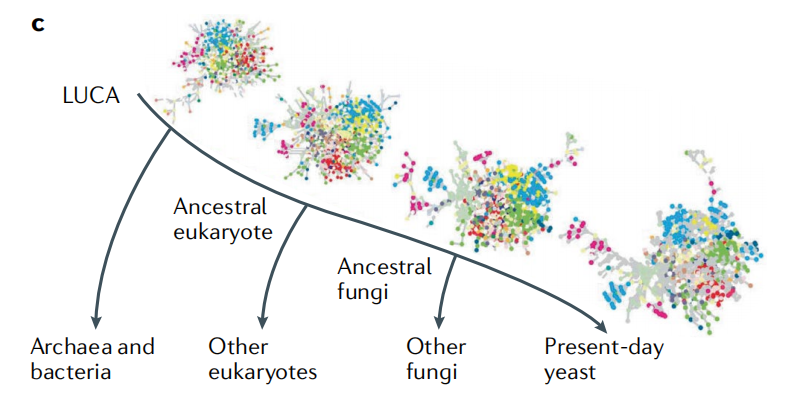
图5:根据Song– Havlin–Makse (SHM)模型及重整正则化,可以重现出酵母进化过程中不同阶段蛋白质相互作用网络
4. 双曲空间映射,改变对网络几何的描述方法
4. 双曲空间映射,改变对网络几何的描述方法

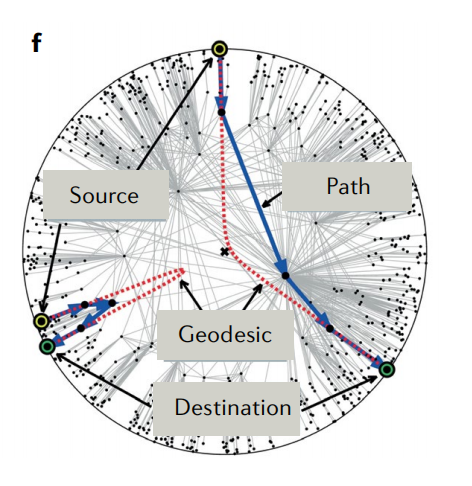
5. 网络中的有效距离决定节点间的传播
5. 网络中的有效距离决定节点间的传播
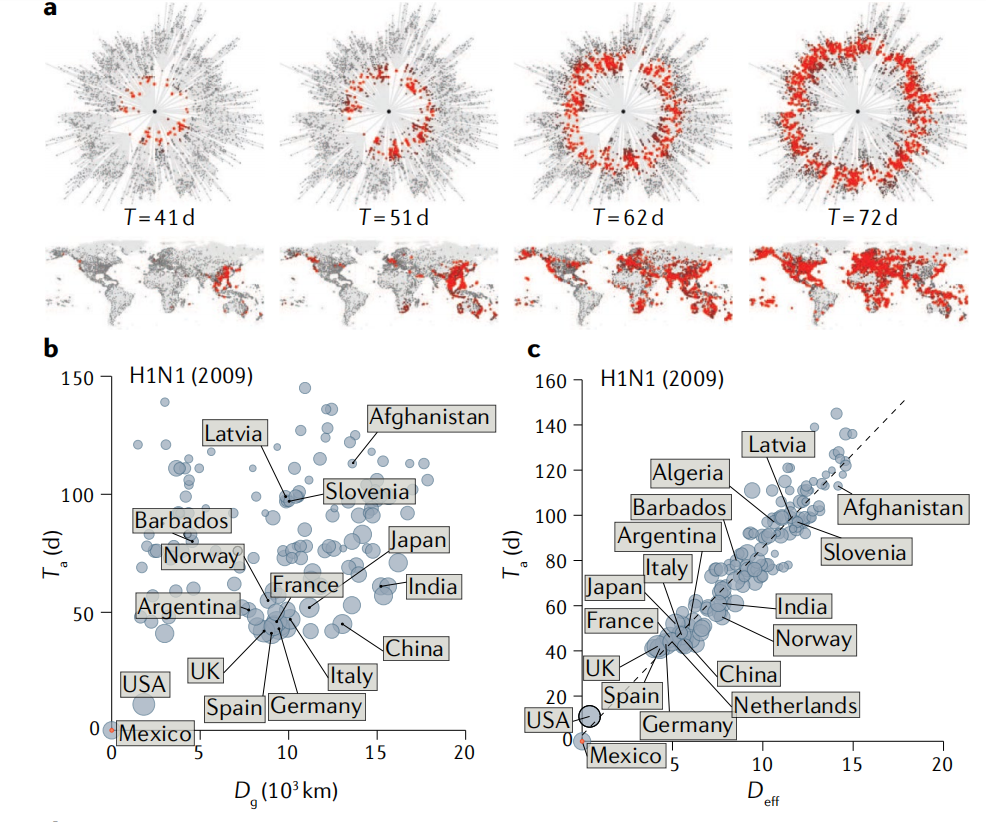
图8:流感病毒传播过程时序图(a)及网络有效距离和传播病例数的对应图(b、c)
6. 回顾网络几何的三个关键词
6. 回顾网络几何的三个关键词
第三是是“运动学距离”(kinematic distances)。网络动力学过程会产生运动学距离,它表征了系统功能的有效几何形状。因此考虑网络的生成过程,能够比单纯考虑网络几何本身,更好地帮助人们理解网络的功能和性质。对于理解网络所描述的复杂系统中的跨层次自组织和由信息交流带来的涌现现象,网络几何也是一个有力的工具。
网络科学新课推荐:网络动力学
点击查看课程详情:
推荐阅读
点击“阅读原文”,追踪复杂科学顶刊论文











