导语


看着迅速增长的离婚率，月老又开始担心起自己的饭碗了。明明很清楚世间男女的理想另一半是谁，无奈一志愿重合太多，只能调剂一下了。咳咳，现在补补课应该还来得及。3 月 16 日瑞士弗里堡大学张翼成团队发表在 Physics Reports 上的综述文章不仅对稳定婚姻问题进行了概述，还讨论了该问题与数学、生物学等学科的关联，尤其是 SMP 在物理学中的理论、应用与最新进展。

陈昊 | 作者

邓一雪 | 编辑


 

论文标题：

The Stable Marriage Problem: An interdisciplinary review from the physicist‘s perspective

论文地址：https://www.sciencedirect.com/science/article/pii/S0370157321000843


稳定婚姻问题起源于数学，随后在经济学得到发展，且在许多领域都表现出了很好的启发性。该问题于 1962 年在 Gale 和 Shapley 的开创性文章[1]中首次出现，并引起了许多科学领域（如物理学、经济学、计算机科学）的关注。3 月 16 日，瑞士弗里堡大学张翼成团队发表在 Physics Reports 上的综述文章对稳定婚姻问题进行了全面概述，着重强调了它的多学科性，尤其关注物理学领域针对该问题的最新成果。
 
 



1. SMP问题介绍




稳定婚姻问题（Stable Marriage Problem，SMP）面向一个由两种不同集合组成的系统，两种集合间的元素需要依照各自的偏好进行一一配对。为了便于理解，通常假设这两个集合各包含 N 位待匹配的男士与女士，每个人都有其对异性的偏好列表。SMP 的最终目的是实现两个集合的稳定匹配，即不存在任何一对男女愿意为彼此放弃当前的伴侣。

表 1 SMP 问题示例
 
以表 1 中 N=3 的 SMP 问题为例，每个人的损失计算规则如下：如果m1与w1配对则损失为 1（表示为x1, 1=1），因为w1是m1的第 1 选择；而w1与m1配对的损失则为 2（表示为y1, 1=2），因为m1是w1的第 2 选择；同理有x2, 3=2、y3, 2=2等等。

一个完整的匹配解 M 可以表示为M={(mi, wj); i,j=1,…, N}，因此针对规模为 N 的系统，我们可以得到N!种可能的匹配解，SMP 问题需要解决的就是寻找其中的稳定解（stable solution）。在稳定解下不存在任意一对 (mi, wj) 使得mi与wj都愿意为彼此放弃当前的伴侣。图 1 为表 1 中提到的示例的两个解，根据上述介绍易知左侧为稳定解。
 
图 1 SMP 问题的解：左侧为稳定解，而右侧为不稳定解。
 




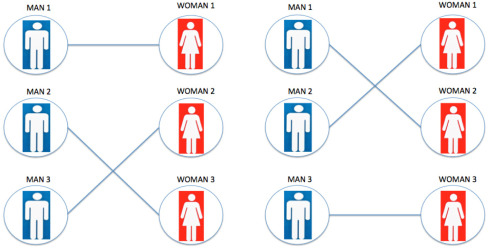
2. GS算法介绍




当 N 很大时，寻找 SMP 的稳定解并非易事。为解决该问题，Gale 和 Shapley 于 1962 年提出了第一个也是最著名的寻找 SMP 特定稳定解的方法：Gale-Shapley（GS）算法[1]。GS 算法有两个版本，分别以男士和女士为导向。两种版本的机制是相同的为简单起见这里仅介绍男士主导的版本：

1. 开始时，所有男士和女士都是单身。

2. 选择一位单身男士mi根据其偏好列表对女士求婚：

a. mi向他的偏好列表中没有追求过的最钟爱的女士wj求婚。
b. 如果wj正处单身，则二人订婚。
c. 如果wj已经与另外一位男士mp订婚且yj, p<yj, i，则wj回绝mi，mi依然保持单身。
d. 如果wj已经与另外一位男士mp订婚且yj, p>yj, i，则wj接受mi，mp变为单身。
3. 算法会重复步骤 2 直至所有男士都找到其伴侣。

可以证明该算法可以收敛到稳定解，且会得到对男士而言最好的解决方法，即尽可能地优先满足男士的需求（具体证明参考原文第四部分）。女士主导的版本与上述算法等价，只是追求者变为了女士。
 
本节介绍了最简单版本的 SMP，除此之外该综述还针对多种 SMP 变体进行了介绍。如信息完全情况下的全局最优解与最小化男女不平等的解，以及男女人数不平等或偏好列表关联不完整情况下的解。
 




3. SMP与物理学




3.1 SMP 的物理解释

如前文所述，SMP 的稳定条件与优化过程都是值得研究的，物理学家对于后者尤其熟悉：物理学中会遇到许多不同类型的优化问题，这些问题需要优化距离、速度、事件等多种物理量。而 SMP 可以作为组合优化问题来研究。众所周知，平衡统计力学与组合优化有着共同的根源[2]。以对相变的研究为例，其研究对象不需要局限于物理系统，而可以扩充为多种组合优化问题，如随机网络上的渗流现象。因此物理学与 SMP 优化的关联是十分自然的。
 
正如前文所说，SMP 的目的是寻找使每个个体都都满意的配对方案。这种情况下每个人都在考虑自身而非整体的利益。这样的稳定形式称为纳什均衡，原文在第六部分（SMP 与经济学的关系）对其进行了详细的描述。而在物理学家来看，SMP 还存在另一种有趣的稳定状态：全局最优解（global minimum solution 或 Ground State），即，使所有人的总损失最小化的解。总损失可以定义为每个个体损失之和，即 X+Y。
 
围绕两种不同的优化目标，作者提出了一些有趣的问题：两种优化目标有多么不同？它们面对外部扰动的稳定性如何，或者说，真实系统如何达到稳定状态？作者从这些问题出发，对两种优化目标进行了定量与定性分析，阐明了全局最优解依然倾向于让个体做出自私的决定。

从定性的角度来讲，全局最优解表示的模型中像是存在着一个媒人从中撮合男女双方，这使得结果对整体最优。而稳定解表示的模型则更像是一个信息完全公开的自由婚恋市场，每个人都理性地关注自己的利益。
 

3.2 稳定解的数量

 
为了进行对两种优化目标的定量分析，作者对 SMP 进行了更加符号化的描述。首先需要补充“阻塞对（blocking pair）”的概念：给定一个匹配策略 M，如果 m 和 w 并非情侣而二人都希望成为彼此的情侣，则称(m,w)为一个阻塞对。由此我们可以重新定义稳定解：一个不存在阻塞对的匹配策略。其次，我们可以使用 y(w,m)表示 m 在 w 的偏好列表中的排名，同理也可以使用 x(m,w)来表示 w 在 m 的偏好列表中的排名。这种排名可以与统计物理学中能量的概念相对应，因此下文中，x 和 y 将表示能量。在统计力学中，系统通常会向能量最小化的方向演化。与之不同的是，SMP 所需达到的稳定解不是能量最小的解。
 
上文已经介绍了一种寻找稳定解的有效方法：GS 算法，通常来说它也被称为 GS 理论[1，3，4]。GS 理论通过证明至少存在一个稳定解回答了一个有关 SMP 的基本问题：稳定解是否存在？

根据 Knuth 的理论[5]，针对规模为 N 的 SMP 问题，在N!种匹配策略中随机选择一种，该策略为稳定解的概率 P 为


其中xi=x(i,i)表示mi与wi结婚的能量（为方标表述，具有相同下标的男女即为特定策略 M 给出的情侣）。公式 1 中的积分只能针对很小的 N 进行计算，为此 Boris Pittel 在其文章[6]中对 N 趋于无穷时的情况进行了估计：


其中Γ(N)为第二类欧拉积分，Γ(N+1)=N!。

随后 Dzierzawa 和 Omero[7]发现 Pittel 的估计在数值上存在很大误差，为此他们重新推导出新的近似公式如下：


其中 S 为规模为 N 的 SMP 中稳定解的近似数量。上述两近似公式的详细推导过程参看原文。
 

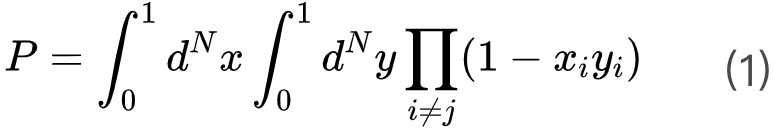
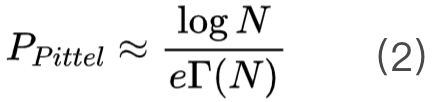
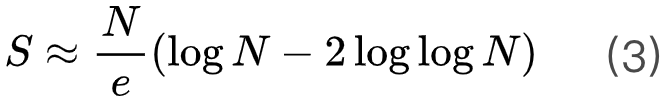
图 3 稳定解的平均数量 每个数据点均为为 200 次随机实验平均得到。虚线为公式 3 的理论值，实线为 Pittel 方法的理论值。[7]


3.3 男性与女性的 GS 能量

上文对男性导向的 GS 算法进行了描述。有趣的是，尽管男性在该过程中多次受挫，且最终只能得到一次积极的回应，却能得到最优的稳定解。而女性则掌握着拒绝的权力，却会得到最糟糕的稳定解。通过计算男性与女性的能量，我们可以验证上述现象。

如果我们使用 r 来表示男性主导的 GS 算法中男性的平均请求次数，则有


使用 r 分别表示男性与女性的总能量 X、Y 有


上述公式的详细推导过程参见原文，图 4 为不同规模 SMP 问题下男性与女性能量的可视化。

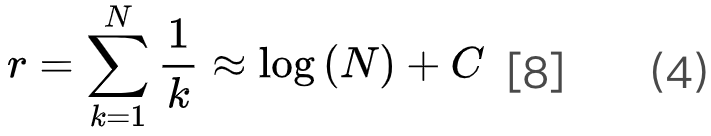
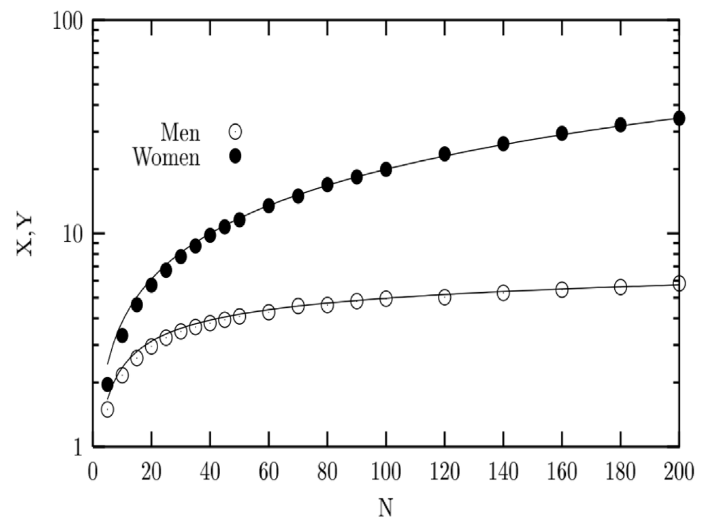
图4 GS 能量 男士主导的 GS 算法中男性与女性的能量，其中 Y 轴为对数坐标。[7]


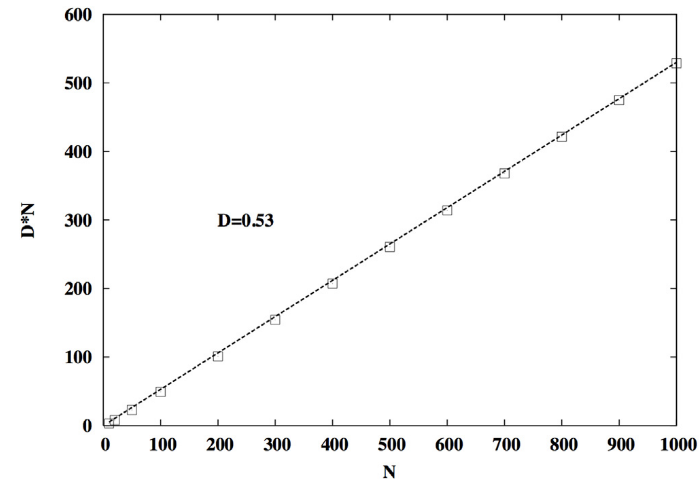
3.4 稳定解与全局最优解的比较


除上述对稳定解的分析外，文章还使用统计物理方法介绍了全局最优解对应的能量的求解方法，图 5 为全局最优解 GS 能量与系统规模的关系，受篇幅限制这里不做展开。

图 5 SMP 基态能量 横坐标 n=N/2
 
研究稳定解与全局最优解的关系是十分有必要的，这可以帮助我们理解个体的自私行为与社会最佳状态的关系。文章证明了稳定解与全局最优解之间存在着一个能隙。与 SMP 基态能量相比，稳定解存在着 19%的改进空间。在[9]中，Lage Castellanos 和 Mulet 介绍了以下指标：


该指标衡量了 a 与 b 两种状态间不同情侣组合的数量，我们可以将其视作两种状态间的距离。如图 6 所示，两种状态间的距离为 0.53。这意味着两种状态中约有 50%的情侣组合是不同的。

图 6 全局最优状态与稳定状态间的距离
 




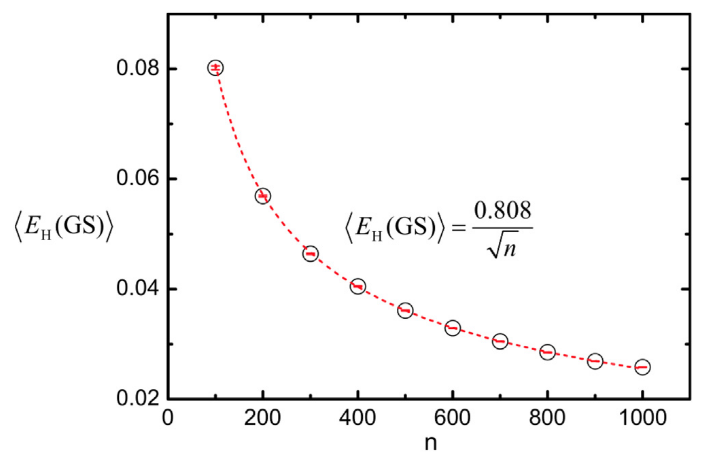
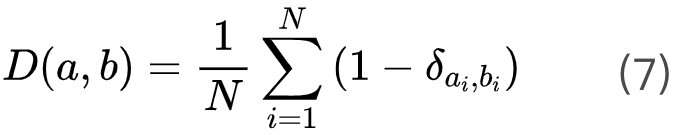
4. SMP与其他学科




4.1 SMP 与生物学

微生物群落是指可以存在于不同类型环境（如土壤、海洋甚至人体）中的微生物群体。尽管这些群落涉及不同类型的微生物，并且可能非常复杂（数千种不同的物种可以在很小的体积内共存），但科学家已经证明，它们通常是以多种稳定状态存在，不同稳定状态有着不同的共存物种比例[11]。

通常来说，每种微生物都有其特定的营养素偏好列表，当一个微生物群落暴露在营养素环境中时。他们便会依照列表依次摄取营养。使用 SMP 来描述微生物群落演化可以优雅地证明多种稳定状态的存在，以及这些状态之间的转换及恢复能力。在这种情况下，婚姻关系表现为微生物种类和营养素之间的一一匹配。在更一般的模型中，所有的微生物都可以利用所有的营养素。在实际情况中，微生物只能摄取部分营养素，这一情况可以通过偏好列表不完整的 SMP 变体来进行分析。

图7 微生物群落的动态演化 顶部方框显示了微生物和营养素的偏好列表。（A）展示了向原本处于最佳状态的系统中加入微生物 M3 后系统的演化过程；（B）展示了向生态系统中加入营养素 N3 后系统恢复最佳状态的过程。[12]


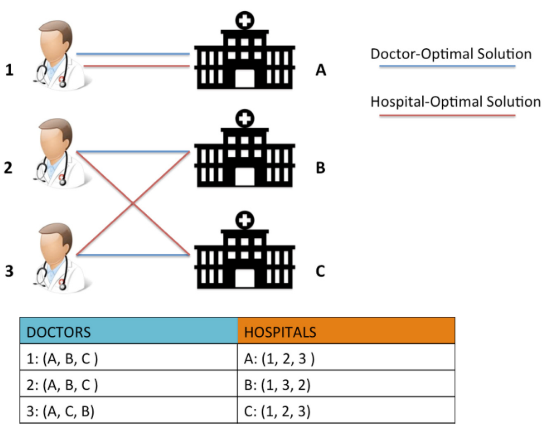
4.2 SMP 与经济学

经济领域是 SMP 最成功的领域之一。到目前为止，许多市场都非常适合使用稳定匹配理论进行建模。2012 年 Shapley 和 Roth 就因其对稳定匹配理论的理论与实验贡献而被授予了诺贝尔经济学奖。

医生分配到医院的问题是是 SMP 的主要应用之一，它是通过匹配理论研究的第一个问题，并启发了随后的大部分工作。20 世纪 40 年代，稀缺的医学生资源迫使美国的医院为低年级的学生提供实习机会，这时的部分学生甚至还没有确定自己的研究领域。由于市场的火爆，如果医院的实习邀请被拒绝，则很可能会错失向其他学生提出邀约的机会。
 
图8 医生分配到医院问题

通过上述方式构造的市场显然会存在不稳定的匹配，因为没有足够的时间来提出对双方都有利的报价。为解决该问题，医院规定了报价的回应期限，迫使学生较早地做出决定，而没有时间知道他们是否会收到更好的报价。为解决该问题，美国在上世纪中叶提出了国家居民匹配计划（NRMP），Roth 的工作[10]证明了 NRMP 算法与标准 GS 算法相同。
 
除上述学科外，原文还讨论了 SMP 在数学、计算机科学等领域的相关研究，并展示了理论结果、应用，以及受其启发的多种模型。
 




5. 总结




SMP 本身并不复杂，但它却引起了人们的极大兴趣，并有着广泛的应用场景。SMP 是对现实的理想但合理的表述，它抓住了许多二分系统的本质。由 SMP 原理出发，可以得到许多同样简单但不平凡的模型。以坐座位问题（Seating Problem）为例，将 N 个人（不区分男女）安排在一个有着 N 个座位的圆桌上，每个人都有一个对相邻座位上的人的偏好列表。由此可以得到多种安排座位的方式，问题的目标是找到其中的最优解使得任何人都不希望更换自己的座位。
 
 

参考文献


[1] Gale, D., and L. S. Shapley. “College Admissions and the Stability of Marriage.” The American Mathematical Monthly, vol. 69, no. 1, 1962, pp. 9–15. JSTOR, www.jstor.org/stable/2312726. Accessed 14 Apr. 2021.

[2] Kumar P R, Wainwright M J, Zecchina R. Mathematical Foundations of Complex Networked Information Systems: Politecnico Di Torino, Verrès, Italy 2009[M]. Springer, 2015.

[3] Gusfield D. Three fast algorithms for four problems in stable marriage[J]. SIAM Journal on Computing, 1987, 16(1): 111-128.

[4] Dubins, L. E., and D. A. Freedman. “Machiavelli and the Gale-Shapley Algorithm.” The American Mathematical Monthly, vol. 88, no. 7, 1981, pp. 485–494. JSTOR, www.jstor.org/stable/2321753. Accessed 20 Apr. 2021.

[5] Donald E K. The art of computer programming[J]. Sorting and searching, 1999, 3: 426-458.

[6] Pittel B. The average number of stable matchings[J]. SIAM Journal on Discrete Mathematics, 1989, 2(4): 530-549.

[7] Dzierzawa M, Oméro M J. Statistics of stable marriages[J]. Physica A: Statistical Mechanics and its Applications, 2000, 287(1-2): 321-333.

[8] Omero M, Dzierzawa M, Marsili M, et al. Scaling behavior in the stable marriage problem[J]. Journal de Physique I, 1997, 7(12): 1723-1732.

[9] Lage-Castellanos A, Mulet R. The marriage problem: From the bar of appointments to the agency[J]. Physica A: Statistical Mechanics and its Applications, 2006, 364: 389-402.

[10] Roth A E. The evolution of the labor market for medical interns and residents: a case study in game theory[J]. Journal of political Economy, 1984, 92(6): 991-1016.

[11] Franzosa E A, Hsu T, Sirota-Madi A, et al. Sequencing and beyond: integrating molecular’omics’ for microbial community profiling[J]. Nature Reviews Microbiology, 2015, 13(6): 360-372.

[12] Goyal A, Dubinkina V, Maslov S. Multiple stable states in microbial communities explained by the stable marriage problem[J]. The ISME journal, 2018, 12(12): 2823-2834.


（参考文献可上下滑动查看）



复杂科学最新论文


集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅：



推荐阅读



点击“阅读原文”，追踪复杂科学顶刊论文