项亦子 | 整理
十三维 | 审校
王建萍 | 编辑

现实世界是由多种主体、多种关系组成的复杂系统。不同系统结构在网络中表现为节点(nodes)与边(edge)的不同质性。但在有些情况下,用普通的图并不能完全刻画真实世界的网络特征。例如,在合作撰写论文的网络中,普通图虽然能表示作者之间是否合作,但是不能表示出是否有三个或者更多的作者合作来写一篇论文。
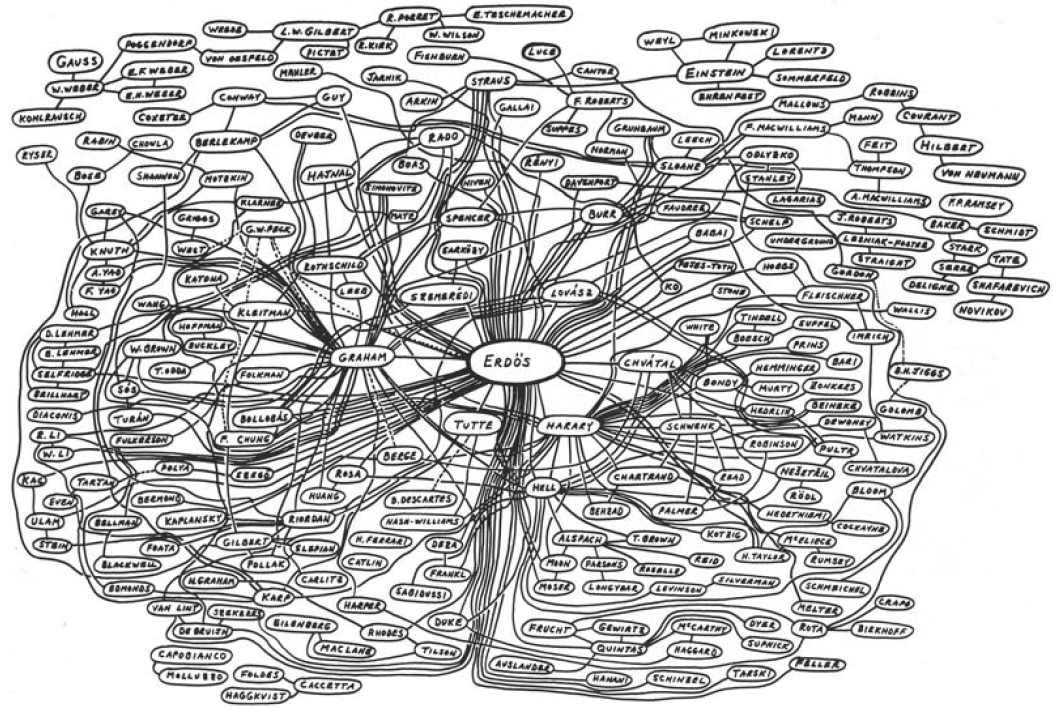
(数学中著名的 Erdos number 网络是普通图,通过连边我们可以看到 Erdos 或其他数学家之间的合作,但是无法看到三个或三个以上数学家之间的合作关系。即使连接多个数学家节点也仅代表两两之间有过合作而非有过共同合作)
因此数学家 Berge 于20世纪60年代提出了一种新的图理论:以作者为节点,以成果为边集,完美描述了该类网络特性,这就是超图(Hypergraph),或称为无向超图。随后有学者对有向超图理论、超图的超回路、着色和t-设计(t-design)等方面进行了研究。
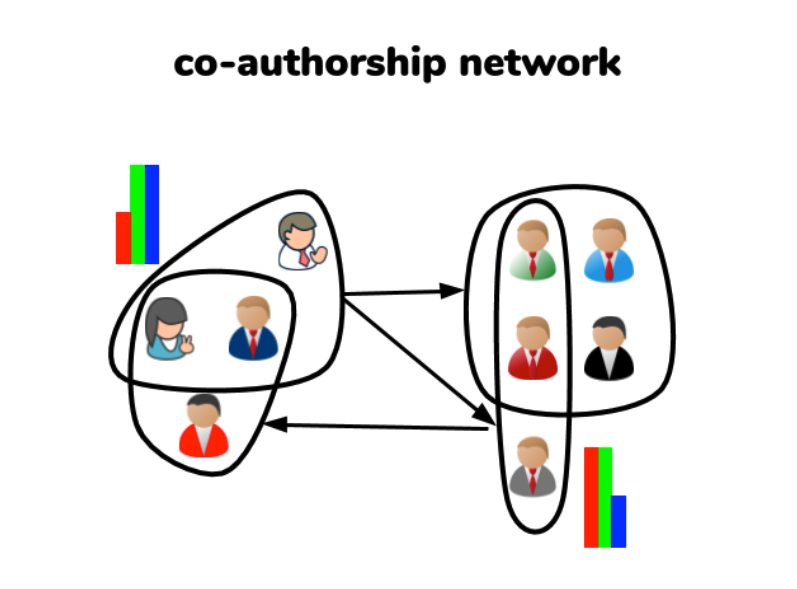
(基于超图的合作网络)
(https://openreview.net/pdf?id=ryestJBKPB)
那么如何用数学语言来描述超图呢?简单而言,对我们熟悉的普通图,一个边只能和两个顶点相连;而对于超图,则推广为广义的边,即可以和任意个数的顶点相连的超边(hyperedge)。
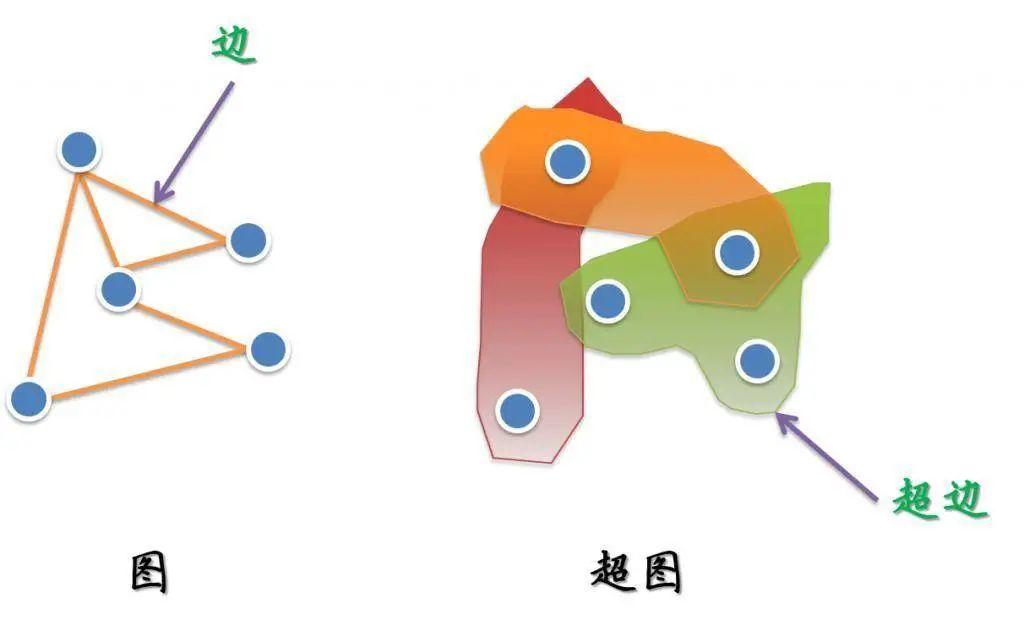
(图和超图)
因此超图本身就是一种广义的图。其严格的数学定义如下[1]:
超图H是一个有序二元组 H=(X,E), 其中X是一个以节点或顶点(vertices)为元素的非空集合,称为顶点集;E是X的一组非空子集簇,其元素被称为边或超边。
因此,若P(X)是X的幂集,则E是 P(X)∖{∅} 的一个子集。在超图H中,顶点集的大小被称为超图的阶数(order of the hypergraph),边集的大小被称为超图的大小(size of the hypergraph)。
超图有许多种,其中有一种叫做k-匀齐超图(k-uniform hypergraph,或译作k-一致超图)。它指每个边连接的顶点数都相同且等于k的超图。因此2-匀齐超图就是传统意义上的图即“普通图”,研究普通图的图论为“传统图论”,研究3-匀齐超图以上三元或多元组的集合的即为超图理论。
超图是有限集合的子集系统,是离散数学中最一般的结构。早期经典的定理有Sperner定理和Ramsey定理等。既然“超图”是普通图的推广,基本概念和定义都是图的相应概念和定义的平移和推广,这方面已取得了一些重要结果,如 Erdös-Ko-Rado定理等。Berge 写了一本专著“Hypergraphs”对其做了系统的总结。
下面我们用两个生活中的例子来介绍Sperner定理和Erdös-Ko-Rado定理。
民以食为天,定菜谱是家家户户每天都要遇到的实际问题。为了健康,现代人讲究营养多样化,所以每天要使用不同的菜谱。现在我们有如下十五种蔬菜,每个菜谱从这十五种里选取一部分:白菜、萝卜、胡萝卜、青椒、黄瓜、苦瓜、西葫芦、西红柿、莴苣、菠菜、青菜、茄子、洋葱、韭菜、西兰花。一个月内每种蔬菜我们都使用过,即三十个菜谱有三十条边(即“超边”,后文一律称为“边”),形成了在十五种蔬菜上的超图。那么问题来了:使用这十五种蔬菜,最多能做出多少个不同的菜谱?
根据 Sperner定理,这个数是不超过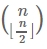 的。上图的圆括号就是我们高中学过的“组合”的意思,注意n/2外的半个方括号是“取整”的意思。所以在这n=15种蔬菜集合上的简单超图,其边数最多为6435条。这里简单超图(Simple hypergraph)的概念很重要,它作为超图任意两条边都互不包含。比如你不可以一天的菜谱定为(青菜,萝卜),另一天的菜谱定为(青菜,萝卜,黄瓜)。真还别小看这十五种普通蔬菜,它们一共可以做出每天都不同的6435天大约十七年半的
菜谱。再问一个问题:现在这15种蔬菜,每个菜谱使用k≤7种蔬菜,且任何两个不同菜谱至少使用一种相同蔬菜,我们可以最多做出多少个这样的菜谱呢?
根据Erdös-Ko-Rado定理,当n≥2k,一个n阶交k-匀齐超图最多包含
的。上图的圆括号就是我们高中学过的“组合”的意思,注意n/2外的半个方括号是“取整”的意思。所以在这n=15种蔬菜集合上的简单超图,其边数最多为6435条。这里简单超图(Simple hypergraph)的概念很重要,它作为超图任意两条边都互不包含。比如你不可以一天的菜谱定为(青菜,萝卜),另一天的菜谱定为(青菜,萝卜,黄瓜)。真还别小看这十五种普通蔬菜,它们一共可以做出每天都不同的6435天大约十七年半的
菜谱。再问一个问题:现在这15种蔬菜,每个菜谱使用k≤7种蔬菜,且任何两个不同菜谱至少使用一种相同蔬菜,我们可以最多做出多少个这样的菜谱呢?
根据Erdös-Ko-Rado定理,当n≥2k,一个n阶交k-匀齐超图最多包含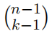 条边,这里n阶就是指超图的顶点个数为n,交超图是指任意两条边都有公共顶点的超图(因为要求菜谱有相同蔬菜)。考虑n=15, k=7,答案是3003种。
进入信息时代,信息科学和技术对人类社会各个领域都产生着巨大的影响,也为创建发展新的数学理论提供了源泉、机遇和动力。包括随着生命科学等领域的不断发展,人们要研究处理的系统越来越庞大,越来越复杂。因此集成化就成了一个重要方向,即把一个大系统化为子系统的集成。反映在数据库理论中,就是把大数据库化为小数据库的联合。首先把数据库的属性集合化为其子集合的并,形成数据库图式。信息科学的发展,特别是数据库理论的发展为超图理论的发展注入了新的活力,赋予了新的内涵,给予了巨大动力。
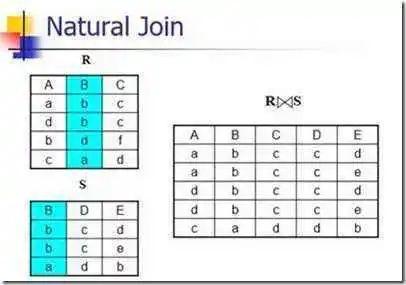
关系数据库里的数据依赖理论中的中心问题是一个关系(即一张表)可以信息保持地分解为若干子关系(即子表),使得原始关系可以由这些子关系自然连接产生。
条边,这里n阶就是指超图的顶点个数为n,交超图是指任意两条边都有公共顶点的超图(因为要求菜谱有相同蔬菜)。考虑n=15, k=7,答案是3003种。
进入信息时代,信息科学和技术对人类社会各个领域都产生着巨大的影响,也为创建发展新的数学理论提供了源泉、机遇和动力。包括随着生命科学等领域的不断发展,人们要研究处理的系统越来越庞大,越来越复杂。因此集成化就成了一个重要方向,即把一个大系统化为子系统的集成。反映在数据库理论中,就是把大数据库化为小数据库的联合。首先把数据库的属性集合化为其子集合的并,形成数据库图式。信息科学的发展,特别是数据库理论的发展为超图理论的发展注入了新的活力,赋予了新的内涵,给予了巨大动力。
关系数据库里的数据依赖理论中的中心问题是一个关系(即一张表)可以信息保持地分解为若干子关系(即子表),使得原始关系可以由这些子关系自然连接产生。
我们可以把关系数据库中的任意一个自然连接看作一个超图,属性是顶点(如上图的A、B、C、D、E),关系图式即关系的属性集合是边(如上图的ABC、BDE)。Fagin,Zaniolo提出了多值依赖的概念,这一概念提供了将一个关系可信息保持地分解为2个关系的充分必要条件。信息保持地分解的一般条件称为连接依赖,是由Rissanen提出来的。
超图与普通图不同,超图可以捕获社交和通信网络中的高阶交互,这些交互超越了成对关系的简单联合。比如微信朋友圈的数据结构是基于普通图的复杂网络,也就是有朋友关系的两人之间用一条边连接;而微信群的数据结构不就是基于超图的超网络吗?一个群也就是在多人之间建立一条超边连接。在Dynamic Shortest Path Algorithms for Hypergraphs一文中,作者考虑超图中的最短路径问题。他们开发了两种算法,用于在动态网络中查找和维护最短的超路径,同时具有权重和拓扑变换。这两种算法是第一回用于解决超图中完全动态最短路径问题的算法。作者分析了算法的时间复杂度,并用随机超图对多通道多无线电网络中的节能路由以及安然电子邮件数据集进行了仿真实验。使用安然电子邮件数据集的实验展示了他们所提出的算法在社交网络中的应用。
20世纪80年代,信息科学家研究数据库理论时,就发现超图与数据库密切相关,而超图圈的传统定义与数据库的性质相差甚远,之后他们引入了无圈超图的概念。这不是一个直观定义,而是由运算过程来界定的。我们称之为超图的无圈公理。他们证明了由无圈公理界定的无圈超图在数据库理论中十分有用。后来的理论成果也显示了无圈公理是科学的。无圈公理构成了无圈超图理论的基础。
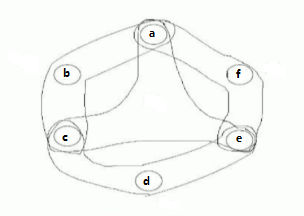
要理解无圈公理,必须先理解“耳朵”这一概念。耳朵就是,一条边e称为超图的一个耳朵,如果存在另一条边e’使得在ee’中每个顶点都是孤立的。孤立顶点是一个仅属于超图的某一条边的点。另,如果e的所有顶点都是孤立的,则e也是一个耳朵。无圈公理就是,一个超图可以通过重复移去耳朵变为空集,这个过程也被称为Graham约简。满足无圈公理的超图被称为无圈超图,一个无圈超图的部分超图可能是有圈超图。超图的这种性质是普通图所没有的。例如下图
超图 ε={abc,cde,efa,ace},显然 b,d,f 都是 ε 的孤立顶点,而abcace=b,cdeace=d,efaace=f,所以 abc,cde,efa 都是 ε 的耳朵。而aceabc=e,acecde=a,aceefa=c,所以边ace不是ε的耳朵。按照传统图论定义,这个超图有1个长度为3的圈和3个长度为2的圈,而按新定义这是个无圈超图,因为它可以通过重复移去耳朵变为空集(移去abc,cde,efa 后移去剩下的耳朵ace。为什么这时ace也是耳朵了呢?因为最后ace的所有三个顶点都是孤立顶点)。而它的部分超图 ε’ ={abc,cde,efa}没有耳朵,则是有圈的。
现代的超图研究中,关于严格(d)-连通 k-匀齐无圈超图(“严格(d)-连通”表示任何两条边的交点数目小于等于d个)的显式的计数公式蕴含了传统图论中关于树的数目的著名的Cayley公式。而k-匀齐线性无圈超图(“线性”表示任何两条边的交点数目小于等于1个)的隐式的计数公式可以推出传统图论里的关于森林数目的Takacs公式。这些结果都是从超图的无圈公理推导出来的,这显示无圈公理是科学的,就像爱因斯坦相对论的公式包含了牛顿力学的特殊情况一样。
那么什么是超图的圈呢?Wang和Lee给出了超图圈的一个新定义。Wang将这个定义做了修正,形成一个公理,称之为圈公理。超图的圈由圈公理来界定。Wang给出了基本定理,证明了圈公理覆盖无圈公理。圈结构在超图理论中是最本质、最基本的。圈公理构成了超图理论的基础。
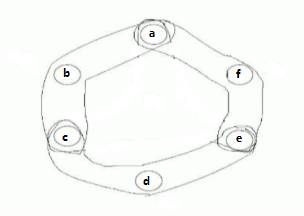
用白话来讲就是“几条边的关节的并不被包含在超图的边中,这几条边就形成了一个圈”。我们用一个例子来验证一下,如下面的超图 ε={abc,cde,efa}:
所以(e0,e1,e2)是 ε 的一个圈。这与之前的那个关于无圈公理的讨论的最后的结果一致,即超图 ε={abc,cde,efa}是有圈的。所以紧接着,Wang又证明给出了基本定理。
ε是由无圈公理界定的无圈超图,当且仅当它没有由圈公理界定的圈。
基本定理使得“无圈”和“没有圈”变成等同了,也使“无圈超图”可以由超图的圈公理来界定。同样,有由圈公理界定的“圈”也和无圈公理界定的“有圈”一致。这显示了圈公理和无圈公理的内在关系。
之后,Wang和Lee合作的关于“超图的独立实圈的最大数目”的公式,是基于圈公理的,其对于普通图的情况等价于著名的图的Euler公式。因此,这就显示出超图的圈公理是科学的,超图的理论基础——无圈公理和圈公理都是自然规律。
Claude Jacques Roger Berger在巴黎大学学习数学,并在获得第一学位后,继续在André Lichnerowicz的指导下继续攻读博士学位。他于1950年开始发表数学论文。同年,他发表了两篇论文。然后,他将论文中的符号演算应用于组合分析,伯努利数,差分方程,微分方程和可加性因子。在1951年,他又发表了两篇简短的论文,即“变换的反面”和“交替的反面”,并宣布了各种结果,这些结果将在其论文中进行全面讨论。他于1953年获得博士学位,在博士论文中,他研究了可以获取完美信息的游戏,在这些信息中,每一步都可能有无数的选择。游戏不一定是有限的,可以无限期延续。贝尔热通过详尽的分析检查了此类游戏的属性。
1952年,在获得博士学位之前,贝尔热被任命为国家科学研究所的研究助理。1957年,他在美国普林斯顿大学任客座教授。参加了与海军研究办公室签订的经济研究项目。在普林斯顿大学期间,论文发表在美国国家科学院院刊上。这是他关于图论的早期论文之一,他较早的工作是关于博弈论和组合论的。他当时正在写他的著作《Théoriedes graphes et ses applicationss 》,刚刚出版了他的《Théoriegénéraledes jeuxàn personnes games 》游戏理论书(1957年)。贝尔热从美国回到法国后,在国家科研中心担任研究主任。同样在1957年,他被任命为巴黎大学统计研究所的教授。《Théoriedes graphes et ses applicationss 》于1958年出版,并于次年出版了他的第三本书《Espaces topologiques,fuctions multivoques fon》。对于30年代初的数学家来说,在几年内出版三本主要著作是一项真正的杰出成就。
王建方是我国现存唯一的一位Erdös数为1的数学家,中科院应用数学所的研究员,主要从事运筹学、组合数学、图论网络最优化的研究。他证明了图论权威学者Harary等人提出的两个猜想,解决了完全等部图的有理性问题和完全等部对称有向图的有理性问题,其结果覆盖了前人在该领域的主要结果,被国外专著引为定理。他从数据库的结构出发,建立了关于超图的路和圈的新公理系统和相关的概念系统,得到了超图圈数的计数公式和最大无圈超图数目计数公式,著名的Euler公式和Cayley公式分别为这两公式的特殊情况,为创建新的超图理论奠定了基础。解决了国际数学大师Erdös提出的关于加边图的带宽问题和猜想并取得了极值结果。对于图荫度、色数、联结数等都取得了系列结果,获中科院科研成果奖和科技进步奖4项,多次应邀访问过美国、日本等地若干大学,访问过匈牙利科学院数学研究所,台湾中央研究院数学研究所,曾被香港中文大学聘为研究员,多次应邀出席国际学术会议做学术报告,作为组委会成员参与筹备组织了三次中—美国际图论和组合学学术会议。
本书介绍了源于数据库理论的超图理论。主要内容为无圈超图理论和超图的圈结构理论。超图的圈公理构成了该理论的基础。这是一个全新的理论分支,且在信息科学、生命科学、经济学、计算机科学等领域有重要应用。这本书专业性比较强,更适合数学和上述领域的研究人员、高校教师、研究生参考使用。
在这里从复杂性知识出发与伙伴同行,同时我们希望有更多志愿者加入这个团队,使百科词条内容得到扩充,并为每位志愿者提供相应奖励与资源,建立个人主页与贡献记录,使其能够继续探索复杂世界。
如果你有意参与更加系统精细的分工,扫描二维码填写报名表,我们期待你的加入!
点击“阅读原文”,阅读超图词条原文与参考文献






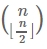 的。上图的圆括号就是我们高中学过的“组合”的意思,注意n/2外的半个方括号是“取整”的意思。所以在这n=15种蔬菜集合上的简单超图,其边数最多为6435条。这里简单超图(Simple hypergraph)的概念很重要,它作为超图任意两条边都互不包含。比如你不可以一天的菜谱定为(青菜,萝卜),另一天的菜谱定为(青菜,萝卜,黄瓜)。真还别小看这十五种普通蔬菜,它们一共可以做出每天都不同的6435天大约十七年半的
的。上图的圆括号就是我们高中学过的“组合”的意思,注意n/2外的半个方括号是“取整”的意思。所以在这n=15种蔬菜集合上的简单超图,其边数最多为6435条。这里简单超图(Simple hypergraph)的概念很重要,它作为超图任意两条边都互不包含。比如你不可以一天的菜谱定为(青菜,萝卜),另一天的菜谱定为(青菜,萝卜,黄瓜)。真还别小看这十五种普通蔬菜,它们一共可以做出每天都不同的6435天大约十七年半的 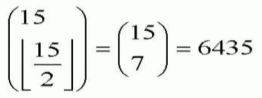
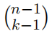 条边,这里n阶就是指超图的顶点个数为n,交超图是指任意两条边都有公共顶点的超图(因为要求菜谱有相同蔬菜)。考虑n=15, k=7,答案是3003种。
条边,这里n阶就是指超图的顶点个数为n,交超图是指任意两条边都有公共顶点的超图(因为要求菜谱有相同蔬菜)。考虑n=15, k=7,答案是3003种。