赵延龙:集值系统的辨识与控制
2024-11-16
826
随着信息化、大数据和智能化的发展,集值系统大量涌现,对系统建模和控制产生了新的需求。集值系统的特点是无法测得输出、状态等系统数据的精确值,只知道它是否属于某个或某些集合。例如:大量医学数据如白血病数据只知道“健康”或“疾病”,大量工程数据如卫星观测数据只知道“百米级”“千米级”等,智能决策问题如雷达目标识别关心的是目标的“真”或“伪”。与传统的精确测量系统相比,集值系统具有可利用信息少和非线性强两大特征,其辨识和控制具有本质困难,需要新的研究视角和理论方法。
研究领域:集值系统,系统辨识,自适应控制,同步控制
赵延龙、王颖 | 作者
集值系统是指无法测得系统数据的精确值,只知道它是否属于某个集合中的系统。它是随着信息化、生物技术和大数据的发展而诞生。产生集值系统的原因主要有如下四点:
神经元是生物体的基本元素, 它由一个细胞体和突触两部分组成。突触分轴突和树突。轴突把本神经元的输出发送至其他相连接的神经元;树突与其他神经元的轴突相连,以接收来自其他神经元的生物信号。轴突和树突共同作用, 实现了神经元间的信息传递。神经元把所有接收到的信息加权求和得到一个总效应。如果总效应大于该阈值电平,那么神经元表现为兴奋状态,反之则为抑制状态。可见,神经元就是一个典型的集值系统。
在数据传输和存储之前首先要将模拟信号转化为数字信号。量化后的数据经过编码后,得到的是低精度的集值数据。众所周知,在数据传输过程中,越小的集值步长会产生越大的数据量, 而数据传输会受到传输带宽的限制,在一定带宽下, 过多的数据会造成信道的拥塞, 使数据传输产生很大的延时甚至失真。在这种情况下,即使每个传感器得到的数据很精确,由于受传输带宽的影响,在传输之前也不得不将信号进一步转换成精度非常低的集值数据。
食物和光照是影响绒孢菌的主要因素, 研究表明绒苞菌厌光并且喜欢食物丰富的环境。为了考察两者中哪一个对绒孢菌的影响更大,设计决策实验,选取两个区域, 一个是光照强但食物丰富的区域,另一个是光照弱但食物缺乏的区域。随后,将绒孢菌均匀分散到两个区域中,经过一段特定时间之后,考察两边绒孢菌的个数,从而反映食物和光照对绒孢菌的影响强弱度。绒孢菌对食物丰富的环境感兴趣,当关心它最终选择哪个区域, 而不是它选择的快慢,那么关心的就是一个集合信息。
精确数据对人们更好地了解系统和控制系统是很有帮助,但为了测量精确数据有可能会对系统造成破坏, 比如光合作用实验和量子系统。为精确地测量叶片在光合作用的内部数据,现有技术是对叶片进行切片处理, 测量叶片内部的反应物和生成物的浓度。不难看出, 这种实验对叶片是一种破坏且不可恢复。为了测量每个时间的实验数据, 需要给很多叶片相同的培养环境, 在所需时间的节点对其中一部分做切片,从而描绘出反应的变化过程。
然而,考虑到叶片个体的差异,这种做法的实验效果一直不理想,且无法对同一叶片重复实验。再如量子系统,为了测量量子系统的精确状态,需要对系统进行测量,然而每次测量都会引起量子态的变化,也就是遵循海森堡测不准原理,因此是否测量,如何测量一直是研究关注的焦点。可以看出,精确测量对系统造成了破坏,如果仅利用叶片毛孔的开关、叶片吸入氧气还是呼出二氧化碳、量子处于哪一类状态等集值数据就可以分析系统内部特征的话,那就会减小这一破坏。
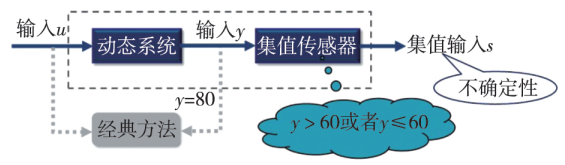
低精度的集值数据在实际应用中起到了越来越重要的作用,从研究的角度而言,以上诸多例子都可以归结为图 1 中的系统。
从结构上来看, 集值系统相比传统系统最大的不同是多了集值传感器部分, 它可以是实际工业中的氧传感器、智能传感网络,也可以是虚拟的量化器以及生物中的比较器。集值传感器使得我们在辨识的时候,无法获取精确输出值,比如 y = 80,只能获得一些粗糙的集值数据,比如 y>60 或者 y≤60。
在粗糙的集值数据下, 如何实现高精度的系统辨识是实际中关心的基本问题。集值测量数据与系统输出之间的误差,既不是有界的,也不具备良好的统计特性。集值数据可用信息少,而且测量器件的非线性强。因此,无法将集值系统放到已有的理论框架下研究。另一方面,已有的辨识的方法,如最小二乘、卡尔曼滤波等算法, 都是基于系统输出构建的, 而集值数据下, 系统输出是不知道的。所以,要研究集值系统,就必须提出新的理论和方法。
该研究方向的核心问题是如何利用粗糙的集值数据完成对目标系统的精确辨识或控制?所涉及的主要科学问题包括:如何做到集值系统的辨识、滤波以及适应控制? 如何融合不同类型的数据,达到更好的辨识或控制效果?基本科学贡献点在于集值系统的可辨识性、辨识的最优性、控制的最优性、数据精度与辨识或控制精度的定量关系等。
集值系统辨识与控制研究具有理论和实际的双重重要意义。从理论角度来讲, 集值数据下的系统辨识和控制研究可以建立一套与现代控制理论平行的系统建模、辨识和适应控制的完整理论体系,这是控制论在新时代背景下的发展。同时,可以定量描述数据精度与系统辨识和控制的相互关系,从控制的角度研究数据精度, 给出最优测量方法以提高数据的使用效率。从实际应用角度来讲,集值信息将极大减弱系统辨识和控制对数据精度的依赖,从而可以有效提高数字传输的效率, 降低测量元件的成本,为与集值系统相关的新兴技术提供新的理论支持。
2.1 集值系统的辨识
针对不同的系统噪声、不同的阈值信息, 可分别构造几种典型系统的辨识算法, 并分析算法的收敛性、时间复杂性以及最优性。
2.1.1 基于二集值输出的线性系统辨识及输入设计方法
针对集值数据, 团队提出了满值输入设计方法和经验分布函数法,给出输入信号充分丰富的条件,并且构造了强一致收敛的辨识算法。进而,研究了其他更复杂的情形,例如,系统不仅有输出噪声还有输入测量噪声以及输入激励噪声,二集值传感器的阈值未知,噪声的分布函数未知等[1-4]。
对最为基本带输出随机噪声的二集值输出的线性系统,辨识的基本困难在于二集值的输出信息少,团队提出满值输入设计和经验分布函数法,给出输入信号充分丰富的条件,并可构造强一致收敛的辨识算法。另外,对于系统不仅存在输出噪声,而且存在输入噪声和输入量测噪声的情况下,以及阈值未知或噪声的分布函数未知时, 均可以构造强一致收敛的辨识算法。
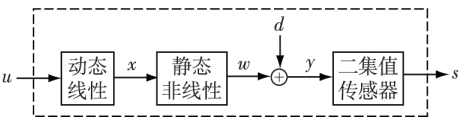
2.1.2 二集值输出的 Wiener 系统辨识
对 具 有 二 集 值 输 出 的 典 型 非 线 性 系 统—Wiener 系统[5], 团队提出了比例满秩信号和联合可辨识性的方法, 克服了二集值输出信息少以及非线性给系统辨识带来的困难, 构造了辨识算法, 并分析了算法的最优性。考虑图2 中的Wiener 系统,系统输出被阈值为C的二集值传感器测量,通过传感器的输出只知y(k) ≤ C 还是y(k)>C。
针对非线性, 团队提出比例满秩信号和联合可辨识性的概念。输入信号的比例特性使得系统的中间变量具有相同的比例性质。结合成比例的状态和二集值的输出信息就构成了关于非线性部分辨识的“核心辨识问题”,而联合可辨识性则保证了核心辨识问题的解决,可以证明关于核心辨识问题的算法是渐近最优的。这样,就把非线性部分的参数辨识出来了。利用已有的非线性部分参数的估计,结合输入信号的满秩特性,对线性部分的参数进行估计。
2.1.3 集值输出的 Hammerstein 系统辨识
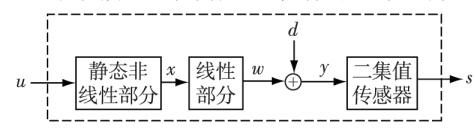
对如图3所示的具集值输出以及多项式形式静态非线性的Hammerstein 系统[6],在不要求非线性部分单调的前提下,针对系统的结构特点,提出比例强满秩信号的概念,构造了辨识算法,分析了算法的最优性。
在二集值输出观测的前提下,辨识 Hammerstein系统比辨识Wiener 系统还要难,这是因为Hammerstein系统与二集值传感器这种非线性元件结合之后,非线性同时存在于输出端和输入端,这为系统辨识带来了一定的难度。为了研究二集值输出的Hammerstein系统辨识,就需要探索新的思路和方法。考虑图3中的Hammerstein 系统,团队重点研了Hammerstein 系统具有多项式形式的非线性部分,且系统的输出被二集值传感器测量。用强满秩周期输入,可以有效克服两端非线性给辨识带来的困难。
2.1.4 递推投影辨识算法
由于二值系统的适应控制问题要求一种在线辨识算法,现有文献[7]提出了递推投影辨识算法,给出了相比已有的递推投影辨识算法更快收敛速度的结果。在算法的收敛性分析时,估计的均方误差包括状态项、中间项和新息项,新息由二值化信息和噪声分布函数构成,且投影确保了估计的有界性。由于中间项和新息项的这些特征,可以得到整个估计的均方误差收敛速度的数量级。
2.1.5 适用更一般条件的递推辨识算法
上述的递推投影辨识算法存在算法设计依赖于噪声分布、仅适用于FIR模型、 要求输入是持续激励的、 待辨识参数的取值范围事先知道等限制,如何放宽上述限制并设计有效的递推辨识算法是值得研究的问题。以下文献[9-11,13,14]从更广的噪声、更一般的系统、更宽的输入、更少的先验等四方面介绍团队在递推辨识算法方面的研究进展:
更广的噪声条件:目前几乎所有量化辨识的文献仅在随机噪声或确定性噪声的前提下研究基于量化数据的参数辨识,缺乏统一两种框架的递推辨识算法。团队基于一种自适应阈值的设计,克服了量化系统在确定性框架中缺乏激励而难以辨识的难点,构造了首个同时适用于确定性噪声和随机噪声的递推在线辨识算法,并分别给出了算法的收敛性分析。
更一般的系统:团队针对在持续激励和固定阈值下具有二值观测的ARMA模型参数辨识问题,克服了回归项信息太少的难点,提出了一种仅使用二值观测值的在线识别算法,包括参数估计以及系统输出值的预测,同时利用耦合的Lyapunov函数,最终证明在一定条件下该算法是收敛的,收敛速度可以达到与迭代次数的倒数同阶,与之前FIR系统参数辨识结论的阶次相同,并且当ARMA模型退化到FIR模型,相应收敛速度达到的条件也相同。
更宽的输入条件:目前集值辨识算法大多要求输入数据的持续激励性,但这在反馈控制系统中很难满足,为此,团队基于时变投影的设计了拟牛顿型递推辨识算法,其步长由标量变为矩阵形式,使得其数据信息更充分的融合到步长设计中,在最弱激励条件下建立了算法的几乎处处收敛性。
更少的先验信息:针对具有二值观测的FIR系统辨识问题,团队首次在无需参数先验信息前提下提出了无投影在线量化辨识算法。创新性地利用算法尾分布的性质,攻克了压缩系数与估计耦合的难点,并在非周期信号条件下给出了目前最优收敛阶的几乎处处收敛速度和均方收敛速度。在此基础之上进一步考虑了衰减激励输入、未知噪声分布和缺少参数位置先验信息情形,分析了集值系统的可辨识性问题,并设计了“分解-重构”型联合辨识算法,实现了对集值系统未知参数及噪声分布参数的联合在线辨识。
2.1.6 最优递推辨识算法
随着集值辨识理论体系的初步建立,一个自然的疑问是如何实现集值辨识算法的性能极限,即如何设计最优辨识算法。由于集值观测的强非线性,其均方损失函数呈现非凸特性,无法通过求解最小损失函数给出最优算法设计。但注意到Cramer-Rao下界可作为估计好坏的评判规则,因此团队在文献[8,12]中建立了集值系统的Cramer-Rao下界来刻画集值数据的信息量。通过分析Cramer-Rao下界的特性,基于自适应权重的设计构造了集值观测下的基于信息矩阵的拟牛顿型加权辨识算法。利用时变投影的设计和高阶矩“加速”思想,攻克了不可交换随机矩阵乘积和步长参数与估计存在强耦合的分析难点,建立了算法的最优收敛速度和渐近有效性。
2.2 集值系统的控制
在集值系统的控制方面, 主要有适应控制[15-17]和同步控制[18-21]这两方面的研究。
2.2.1 适应控制
集值输出系统的适应控制问题与单纯的参数辨识和参数已知时的镇定控制相比要困难得多,原因之一是适应控制与参数辨识算法相互依赖,已有文献中关于集值输出系统的辨识算法的良好性质是以周期输入为前提的,而适应控制中的控制律是根据控制目标和参数估计值而确定的,因此,一般来讲是随机的且不具周期性;原因之二是适应控制下闭环系统更为复杂,表现为 (即使对简单的线性定常系统) 闭环系统的高度非线性和输入、输出的复杂随机性, 输出端的集值信息和估计值的关系也相应地更为复杂。
随着集值系统辨识方面的研究积累和成果系统化,集值系统逐步受到国内外学者的关注,代表性的工作有: 1) 扩展的极大似然方法解决集值系统的辨识问题, 提出了固定数据长度下的无穷步迭代算法;2) 量化滤波算法, 该方法是以量化误差服从正态分布为基础的;3) 鲁棒辨识的方法研究有界噪声下的参数估计问题。然而已有针对集值系统方法由于自身限制均无法做到适应控制。
针对集值系统的适应控制,一个可能可行的思路是:首先将已有工作中的周期输入推广为一般的持续激励输入,在不限制集值信息与参数估计值的相关性的前提下,直接构造在线的面向控制的辨识算法, 然后以这些算法为基础去设计适应控制器,进而借鉴传统的自校正调节思想,完成集值输出系统的适应控制设计和闭环系统的性能分析。
对于一般的集值输出系统,设计这样的控制器是非常困难的。作为这方面的初步性工作,现有文献仅考虑一类单参数的二集值输出系统的适应跟踪控制。我们用一类投影递推算法辨识系统的未知参数,用参数估计和控制输入来调整系统输出的阈值, 根据“必然等价原则”构造适应控制律,在较一般的未知参数先验信息、噪声统计特性和被跟踪信号等条件下,给出了算法的收敛性和收敛速度,证明了闭环系统的稳定性和跟踪的渐近最优性。现有文献将该方法推广到一般线性系统中。
2.2.2 同步控制
多个体的同步控制问题近年来引起了广泛的关注,因为它的应用范围非常广泛, 比如多处理器的负载平衡、移动车辆的协同控制,以及无人地面、空中和水下的交通工具的控制。同步问题旨在设计一种分布式协议,使所有个体都渐近地达到一个共同的状态, 这在合作控制的背景下是非常重要的。
信息是局部的是多个体系统的主要特征之一,每个个体只能获取其邻居的状态信息, 但精确状态值的获取需要非常高质量的网络通信能力,而实际通信过程中往往存在噪声和带宽的限制。因此,在研究多个体同步问题时,有必要考虑除了局部性限制以外的其他因素,即噪声和量化。
考虑含有n个体的多个体系统,为了实现同步,每个个体需要与邻居个体传递信息, 但是由于带宽等因素的影响,邻居个体之间只能传递如下二值信息。为了实现同步,每个个体都需要通过使用其邻居的状态来设计同步控制。但是邻居的状态是未知的,所以每个个体都需要估计邻居的状态,然后根据邻居状态的估计值来设计同步控制。由于每个个体只能获得邻居的二值信息,一种方法是每个个体等待一段时间来收集足够的二值信息,然后利用无截断辨识法对其邻居的状态进行估计; 另一种方法是利用递推投影辨识法对邻居节点进行估计,该算法是在线辨识算法,估计实时更新,个体状态不需要保持一段时间不变,那么控制也就可以进行实时更新。
1) 二时间尺度同步算法: 在小的时间尺度上,每个个体先估计其邻居的状态; 在大的时间尺度 (一些跳跃的时间点) 上,个体根据状态的估计值设计控制率,在该控制下个体的状态会进行更新。重复上述估计和控制过程,就形成了二时间尺度同步算法。从这个算法的结构可以看出,当时间增大到一定程度时,个体用于估计的时间越长,估计会越来越准。但与此同时,在估计上花费的时间就越多,这使得个体状态的更新速度会很慢,可能会影响算法整体上的收敛速度。
2) 递推投影同步算法: 该算法在对邻居节点状态进行估计时,利用递推投影辨识算法,每个个体可以实时地估计邻居个体的状态,然后利用平均原则,用估计值代替邻居状态真值,并取增益步长 1 /( t + 1) 来,实时设计同步控制律。虽然递推投影辨识算法是对固定参数估计的一种算法,状态实时变化时估计性质不一定很好,但是同步控制可使得状态趋于一致,个体的状态在后期就不会有太大变化,这样递推投影辨识算法依然可以实现一个好的估计。最后,通过估计和控制的合作,多个体系统就可以实现同步。
在算法的收敛性分析时,我们分别分析了估计和状态更新的性质,然后联合考虑这两者之间的相互作用关系,最后证明了算法的收敛性和收敛速度。同时,也在理论上证明了递推投影同步算法相比二时间尺度同步算法具有更快的收敛速度。目前,团队将事件驱动机制引入控制器设计中进一步减少通信成本和控制成本。
2.3 集值系统的应用
2.3.1 复杂疾病建模[22-23]
复杂疾病系统就是一类典型的集值输出系统,样本属性只是“疾病”或“健康”,样本的观测维度极高,而且样本量相对较少。要建立复杂疾病的模型,从医学的角度研究人类疾病与遗传的关系,核心问题在于如何利用海量遗传数据找出各种遗传性疾病的遗传规律、发病机制、诊断和防治措施。基因测序技术的不断发展使得研究者可以获得更全面更准确的遗传信息,比如现下流行的全基因组关联分析 (GWAS) 能够检测数以百万计的单核苷酸多态性 (SNPs) 作为单个样本的遗传标记。然而,高昂的测序成本极大地限制了测序的样本数量。数以千计的样本数量与数以百万计的观测维度使得许多传统方法不再有效。
在复杂疾病建模和统计验证方面,我们与美国圣朱迪儿童研究医院合作,基于实际数据成功建立了白血病的集值模型,并构造了新的、更为有效的统计验证方法。
2.3.2 雷达目标识别[24]
雷达目标识别是军事领域的一项重要任务。伴随着弹道导弹制造技术在全球的扩散,出现了反弹道导弹系统,为了突破反导系统,现代弹道导弹都具备先进的防突设施, 其中一项重要的措施就是释放多种形式的诱饵,增加反导系统的拦截负荷。弹道导弹经过攻防之间不断的交互竞争过程,现面临的核心问题就是如何从目标群中识别出真弹头。对于雷达目标识别,出于成本与安全的考虑,不可能通过大量实际试验来获取观测样本。为了提高识别精度,如何利用好小样本获取尽可能精确的估计结果成为一项重要难题。
团队与相关单位合作完成了对真假目标的集值建模。首先对雷达数据进行预处理,将大通量数据降维得到一些特征信息,使得这些特征信息可以尽可能多体现目标与其他物体的差异; 然后利用集值辨识等方法对目标进行分类识别。与已有方法相比,得到了更高的识别率,尤其是在低信噪比时,识别率提高得更为明显,可高达10%。
2.3.3 无拖曳卫星控制[25]
无拖曳控制技术是重力梯度测量卫星的关键技术之一,其目的是为了补偿在轨卫星受到的干扰力及力矩,使得卫星在地球重力场的作用下运行。无拖曳控制的理论显得非常直接,但真正实现高精度或者极低“剩余”加速度的无拖曳控制还面临诸如模型信息缺失、重力梯度仪测量信息饱和受限、对控制精度要求极高等难题。
团队与相关单位合作以重力梯度卫星为对象,研究了无拖曳控制中的干扰估计和位姿联合控制等问题。在重力梯度仪的量程范围内插入多个阈值,从而将精确与量化混杂的饱和约束观测数据近似为多值量化数据,因而可以引入递归投影随机逼近型多值量化数据参数辨识算法实现对阻力增益系数等未知参数的辨识。算法估计值在闭环系统中强一致地收敛到真实值,并得到与精确数据下参数估计算法同阶的几乎处处收敛速度。基于得到的阻力增益系数等参数的估计值,进一步设计带投影的自适应控制器,实现了渐近最优的自适应跟踪控制。
集值系统在网络化和信息化大环境下涌现出来并得到了广泛应用,其系统辨识和控制研究可以建立一套与现代控制理论平行的系统建模、辨识和适应控制的完整理论体系,是控制论在新时代环境下的发展。从应用角度来看,集值信息能够极大减弱系统辨识和控制对数据精度的依赖,从而可以有效提高数字传输的效率、降低工业中测量元件的成本,为生物实验和量子系统等与集值信息相关的新兴技术提供新思路。
集值系统的辨识与控制是一个新兴的研究领域,有很多有价值的问题亟待解决。比如: 1) 对集值系统进行辨识以后,如何利用辨识得到的信息来解决一般信号条件下的适应控制问题?2) 除了考虑集值量测限制外,通信过程中往往会存在时延和丢包,如何在考虑这些因素的情况下实现同步?3) 进一步,如何刻画数据与辨识和控制任务的定量关系,即如何在给定数据条件下实现最优的辨识或控制效果,抑或是如何刻画实现辨识和控制任务所需的最小数据条件?这些问题都具有一定的难度,需要众多科研工作者的广泛关注和积极参与。本文的工作还只是抛砖引玉,相信随着大家对集值系统研究重要意义认识的逐步深入,此方向的研究必将得到更快的推进和发展。
[1] Wang L Y, Zhang J F, Yin G. System identification using binary sensors [J]. IEEE Transactions on Automatic Control, 2003, 48(11): 1892-1907
[2] Wang L Y, Yin G. Zhang J F. Joint identification of plant rational models and noise distribution functions using binary-valued observations[J]. Automatica, 2006, 42(4): 535-547
[3] Wang L Y, Yin G, Zhao Y L, et al. Identification input design for consistent parameter estimation of linear systems with binary-valued output observations [J]. IEEE Transactions on Automatic Control, 2008, 53(4): 867-880
[4] Wang L Y, Yin G, Zhang J F, et al. Space and time complexities and sensor threshold selection in quantized identification [J]. Automatica, 2008, 44(12): 3014-3024
[5] Zhao Y L, Wang L Y, Yin G, et al. Identification of Wiener systems with binary-valued output observations [J]. Automatica, 2007, 43(10): 1752-1765
[6] Zhao Y L, Wang L Y, Yin G, et al. Identification of Hammerstein systems with quantized observations[J]. SIAM Journal on Control and Optimization, 2010, 48(7): 4352-4376
[7] Guo J , Zhao Y L. Recursive projection algorithm on FIR system identification with binary-valued observations, Automatica, 2013, 49(11): 3396-3401
[8] Zhang H, Wang T, Zhao Y L. Asymptotically efficient recursive identification of FIR systems with binary-valued observations[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems. 2021, 51(5): 2687-2700
[9] Wang Y, Zhao Y L, Zhang J F, Guo J. A unified identification algorithm of FIR systems based on binary observations with time-varying thresholds, Automatica. 2020, 135: 109990
[10] Zhang L T, Zhao Y L, Guo L. Identification and adaptation with binary-valued observations under non-persistent excitation condition[J]. Automatica, 2022, 138: 110158
[11] Wang T, Li X, Guo J, Zhao Y L. Identification of ARMA models with binary-valued observations, Automatica,2023, 149: 110832
[12] Wang Y, Zhao Y L, Zhang J F. Asymptotically efficient quasi-newton type identification with quantized observations under bounded persistent excitations[J]. Automatica, 2024, 166: 111722
[13] Ke J M, Wang Y, Zhao Y L, Zhang J F. Recursive identification of binary-valued systems under uniform persistent excitations[J]. IEEE Trans. on Automatic Control, DOI: 10.1109/TAC.2024.3399968, 2024
[14] Ke J M, Zhao Y L, Zhang J F. Joint identification of system parameter and noise parameters in quantized systems[J]. Systems & Control Letters, 2024, 193: 105941
[15] Guo J, Zhang J F, Zhao Y L. Adaptive tracking control of a class of first-order systems with binary-valued observations and time-varying thresholds[J]. IEEE Transactions on Automatic Control, 2011, 56(12): 2991-2996
[16] Zhao Y L, Guo J, Zhang J F. Adaptive tracking control of linear systems with binary-valued observations and periodic target[J]. IEEE Transactions on Automatic Control. 2013, 58(5): 1293-1298
[17] Wang T, Hu M and Zhao Y L. Adaptive tracking control of FIR systems under binary-valued observations and recursive projection identification[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems. 2021, 51(9): 5289-5299
[18] Zhao Y L, Wang T, Bi W J. Consensus protocol for multi-agent systems with undirected topologies and binary-valued communications[J]. IEEE Transactions on Automatic Control, 2019, 64(1): 206-221
[19] Wang T, Zhang H, Zhao Y L. Consensus of multi-agent systems under binary-valued measurements and recursive projection algorithm[J]. IEEE Transactions on Automatic Control[J]. 2020, 65(6): 2678-2685
[20] Hu M, Wang T, Zhao Y L. Consensus of switched multi-agent systems with binary-valued communications[J]. Science China Information Sciences. 2022, 65: 162207
[21]Lu X D, Wang T, Zhao Y L. Event-Triggered control for consensus of multiagent systems with binary-valued measurements[J]. IEEE Transactions on Automatic Control. 2024, 69(7): 4630-4642
[22] Kang G L, Bi W J, Zhang H, Zhao Y L, et al. A robust and powerful set-valued approach to rare variant association analyses of secondary traits in case-control sequencing studies[J]. Genetics. 2016, 205(3)
[23] Zhang H, Bi W J, Cui Y H, Chen H L, Chen J B, Zhao Y L, Kang G L. Extreme-value sampling design is cost-beneficial only with a valid statistical approach for exposure-secondary outcome association analyses[J]. Statistical Methods in Medical Research. 2020, 29(2): 466-480
[24] Wang T, Bi W J, Zhao Y L, Xue W C. Radar target recognition algorithm based on RCS observation sequence—Set-valued identification method[J]. Journal of Systems Science and Complexity. 2016, 29(3): 1-16
[25] Tan S P, Guo J, Zhao Y L, Zhang J F. Adaptive control with saturation-constrainted observations for drag-free satellites — a set-valued identification approach[j]. Science China Information Sciences, 2021, 64: 202202
对复杂动态系统的定量认识与科学调控,系统学与控制论是关键基础。集智学园联合中科院数学与系统科学研究院多位控制科学与工程领域专家共同开设了《控制科学前沿理论与方法》系列课程,为面向控制专业领域学生以及跨领域的学习者做深度科普,帮助学习控制论的核心思想、框架与方法。通过学习这些课程,学生将了解控制论的发展历程,掌握经典和现代控制方法,探索控制系统的美妙之处。此系列课程共计10节,已完结上线。欢迎感兴趣的朋友报名参与!
详情请见:
点击“阅读原文”,报名课程