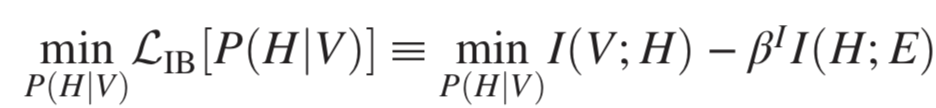因复杂物理系统的分析取决于从众多其他自由度中提取相关自由度的能力。尽管人们对机器学习寄予厚望,但它也带来了可解释性的挑战。研究人员通常不清楚学习到的“相关”特征与物理理论的对应关系。在最近发表在 Physics Review Letters 的一篇文章中,研究人员报告了有助于解决这个问题的理论结果:他们建立了重整化群的场论相关性与信息瓶颈(information bottleneck,IB)理论定义的相关性概念之间的等价性。他们的分析表明,对于由场论描述的统计物理系统,使用IB理论发现的自由度确实对应于具有最低标度维数的算子。他们以数值方式证实了他们的场论预测。研究人员研究了IB算法对物理对称性的依赖性。他们的发现提供了一个连接两个不同理论的方法,以及一个在物理的深度学习应用中能够给出物理可解释性的例子。
研究领域:统计物理,重整化群,临界现象,信息与传播理论
论文题目:
Relevance in the Renormalization Group and in Information Theory
论文地址:
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.126.240601
研究理论模型是物理研究的一个重要方向。然而,对于复杂的系统,确定正确的自由度是什么,并根据这些自由度构建模型,本身就是一个挑战。这个过程是由实验或数值观察驱动的,但在实践中,物理直觉和先验知识对于构建一个足够简单的模型来描述现象的“本质”至关重要[1]。尽管如此,数据本身应该包含完成这项任务的足够信息。一个方案是使用现代计算方法,特别是深度学习(deep learning)[2-4]。使用该算法的一个基本障碍是物理学概念(主要以场论语言表述)与深度学习的理论和实践之间的不匹配,这就是可解释性问题[5]。为了解决这个问题,需要一个能够兼容这两者的框架。与物理学和计算机科学[6-8]密切相关的信息论(information theory)是一个候选者。
在其经典的表述中,信息论不了解信息的内容,专注于其有效传输[9]。尽管通常只有部分信息与问题相关,但事实证明,很难普遍定义“相关性”概念[10],信息瓶颈理论解决了该问题。该理论认为:随机变量中的相关信息由相关性或共享信息定义,具有辅助相关性变量,提供隐式过滤器,用以指示保留哪些内容。
压缩数据以有效地保留隐式定义的相关内容被视为拉格朗日优化问题,该问题最近引入了深度学习算法[12]。然而,在物理学中,已经存在一个基本的和先验的独立相关概念,它基于在重整化群(renormalization group,RG)流中体现的尺度变换下的算子属性 [13-15]。RG相关性是人们所拥有的最精确的定义,可以确定系统宏观物理特性的可观察量。RG直接连接到共形场论(conformal field theories,CFT)的概念中,彻底改变了人们对临界现象的理解 [16-22]。
在这里,研究人员表明RG和信息论的概念,实际上在物理系统中是等价的,即信息论意义上的有关长程属性的信息是由最相关的算子确定的。自从观察到其流动的不可逆性以来,RG背景下的信息丢失一直吸引着人们[23-31]。研究人员引入了RG与压缩理论的联系,它是定量的和可计算的。这使研究人员能够以数值方式验证预测。可以证明,使用IB方法可以从数据中提取最相关的算子,以及有关物理对称性的信息和基于表征分布的内在信息理论量,并且无需调用场论对象。因此,该结果不仅具有理论意义,而且具有实践意义。它提供了一种实现理论任务自动化的途径。
这些结果和深度学习 [32,33] 被用来构建一种有效的算法,即基于神经网络的实空间互信息估计器(real-space mutual information neural estimator,RSMI-NE)[34,35] ],从更大的输入中提取物理上相关的算子,并表征空间相关性、相变(phase transitions)和序参量(order parameters)。研究人员证明RSMI是IB问题的一种情况,这为该数值方法提供了理论基础。
任何数据的相关特征,仅相对于手头的任务有意义地定义,并且它们的识别因数据中可能同时存在的多个“不相关”(针对所提出的问题)结构或规律而变得复杂。信息瓶颈为此类相关特征的无监督学习提供了严格的框架。以“数据”V的联合概率分布和辅助“相关性”变量E作为输入,IB找到V的最佳压缩H,保留有关E的信息。因此,与E的相关性定义了V中的相关内容,而不是任意度量。IB可以表示为以下变分问题:
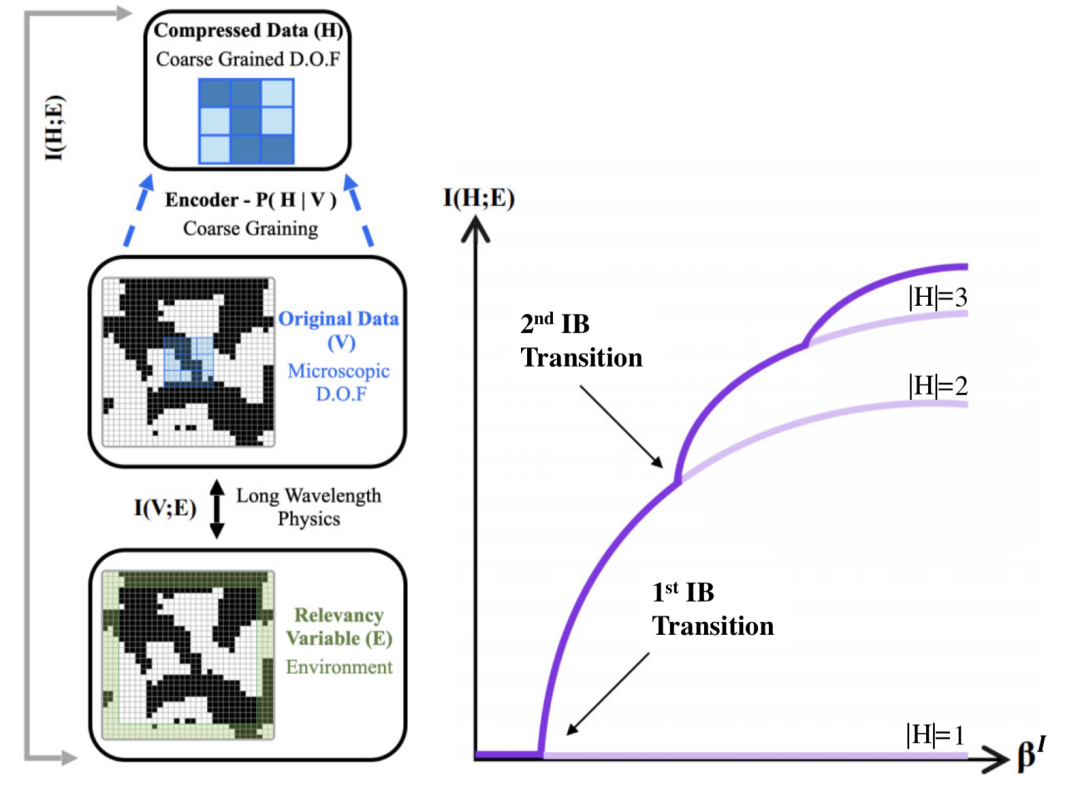
图1:左侧:IB方案的流程图:构建了一个最佳编码器,用于提取有关包含在V中的相关变量E的信息。右侧:IB曲线描绘了相关信息。信息为βI的函数,在转换的临界值产生新的解决方案,具有增加的模数的压缩变量H出现,旧的解决方案成为不稳定最小值。
研究人员需要定义E以确保IB准确保留RG相关信息。在RSMI[36,37]的背景下,研究人员对实空间RG进行了适当的定义:对于表示粗粒度化的区域中自由度边际分布的随机变量V,变量E(“环境”)是系统在变量V非零厚度壳之外的其余部分。
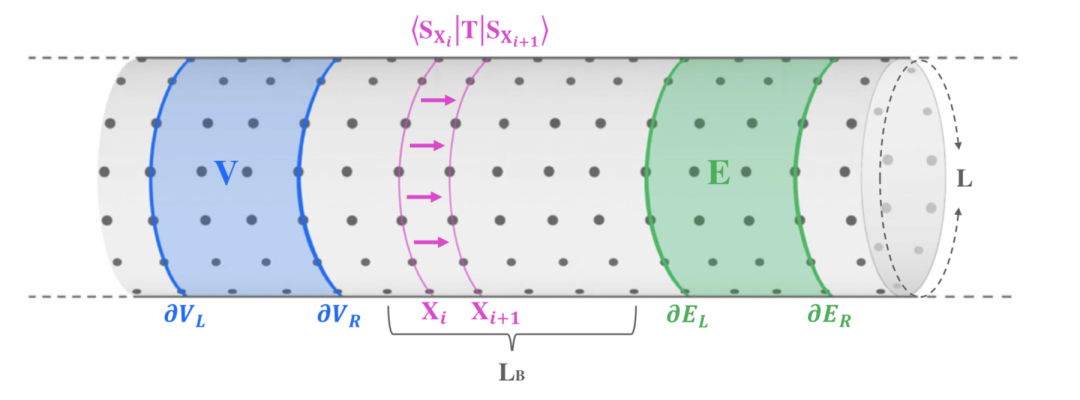
图2:转换矩阵的设置。对于圆柱的系统,IB方程可以用转换矩阵的特征向量来求解,在大尺度L的限制下,转换矩阵的特征向量与CFT数据有关。
RSMI算法[36,37]与IB密切相关。具体来说,它还最大化了相关信息。直观地说,IB提取了βI允许的尽可能多的特征,随着βI的增长而添加它们,而RSMI从一开始就精确地优化了H的最佳特征。因此,RSMI是βI趋于无穷大的情况。由此建立的IB和场论之间的定量联系给出了将任一领域的不同理论和数值方法应用于其对应领域的可能性。
结果具有明确的理论和实践流程:可以完全根据信息理论量来定义和探讨RG意义下的物理相关性,而无需明确提及“算子”、“标度维数”、“场论”等。这些数学对象在信息论方面通常是不可用的——人们可以访问概率分布的样本,但不知道是哪个物理系统生成的,它的相关算子是什么,如何它们用微观自由度表示,或者人们应该计算哪些相关函数。通过形式化和证明物理相关性的信息论概念与RG的等效性,研究人员赋予了它具体的含义,并开发了必要的技术,使其在分析和数值上可量化和可计算。这提供了在面对复杂数据时发现上述问题答案的方法。
在理论方面,考虑到不依赖哈密顿量的概念,应用IB方法在无序和非平衡系统情况下提取相关量是很有前景的。这可能需要更深入地了解IB方程的性质和它们在RSMI-NE算法中的约束版本。研究人员希望使用物理量的信息论公式,结合深度学习的能力,以受控的方式优化它们的算法[34,35,64],这可以为更多理论上可解释的问题提供解答。
[1] P. V. Coveney, E. R. Dougherty, and R. R. Highfield, Big data need big theory too, Phil. Trans. R. Soc. A 374, 20160153 (2016).
[2] G. Carleo, I. Cirac, K. Cranmer, L. Daudet, M. Schuld, N. Tishby, L. Vogt-Maranto, and L. Zdeborová, Machine learning and the physical sciences, Rev. Mod. Phys. 91, 045002 (2019).
[3] V. Dunjko and H. J. Briegel, Machine learning & artificial intelligence in the quantum domain: A review of recent progress, Rep. Prog. Phys. 81, 074001 (2018).
[4] S. D. Sarma, D.-L. Deng, and L.-M. Duan, Machine learning meets quantum physics, Phys. Today 72, No. 3, 48 (2019).
[5] W. J. Murdoch, C. Singh, K. Kumbier, R. Abbasi-Asl, and B. Yu, Definitions, methods, and applications in inter- pretable machine learning, Proc. Natl. Acad. Sci. U.S.A. 116, 22071 (2019).
[6] J. Preskill, Quantum information and physics: Some future directions, J. Mod. Opt. 47, 127 (2000).
[7] D. J. C. MacKay, Information Theory, Inference, and Learning Algorithms (Cambridge University Press, Cambridge, England, 2002).
[8] M. Mezard and A. Montanari, Information, Physics, and Computation (Oxford University Press, Inc., New York, USA, 2009).
[9] C. E. Shannon, A mathematical theory of communication, Bell Syst. Tech. J. 27, 379 (1948).
[10] Y. Blau and T. Michaeli, Rethinking Lossy compression: The rate-distortion-perception tradeoff, in Proceedings of the 36th International Conference on Machine Learning, ICML 2019, Proceedings of Machine Learning Research (PMLR, 2019), pp. 675–685, Vol. 97.
[11] N. Tishby, F. C. Pereira, and W. Bialek, The information bottleneck method, Proceedings of the 37th Allerton Conference on Communication, Control and Computation (Univ. of Illinois, Illinois, 2001), Vol. 49.
[12] A. A. Alemi, I. Fischer, J. V. Dillon, and K. Murphy, Deep variational information bottleneck, arXiv:1612.00410.
[13] K. G. Wilson and J. Kogut, The renormalization group and the ε expansion, Phys. Rep. 12, 75 (1974).
[14] K. G. Wilson, The renormalization group: Critical pheno- mena and the Kondo problem, Rev. Mod. Phys. 47, 773 (1975).
[15] M. E. Fisher, Renormalization group theory: Its basis and formulation in statistical physics, Rev. Mod. Phys. 70, 653 (1998).
[16] A. A. Belavin, A. M. Polyakov, and A. B. Zamolodchikov, Infinite conformal symmetry of critical fluctuations in two dimensions, J. Stat. Phys. 34, 763 (1984).
[17] A. A. Belavin, A. M. Polyakov, and A. B. Zamolodchikov, infinite conformal symmetry in two-dimensional quantum field theory, Nucl. Phys. B241, 333 (1984).
[18] D. Friedan, Z. Qiu, and S. Shenker, Conformal Invariance, Unitarity, and Critical Exponents in Two Dimensions, Phys. Rev. Lett. 52, 1575 (1984).
[19] P. Di Francesco, P. Mathieu, and D. Snchal, Conformal Field Theory, Graduate Texts in Contemporary Physics (Springer, New York, NY, 1997).
[20] J.L Cardy, Scaling and Renormalization in Statistical Physics, Cambridge Lectrue Notes in Physics (Cambridge University Press, Cambridge, 1996).
[21] C. Itzykson, H. Saleur, and J.-B. Zuber, Conformal Invari- ance and Applications to Statistical Mechanics (World Scientific, Singapore, 1998).
[22] D. Poland, S. Rychkov, and A. Vichi, The conformal bootstrap: Theory, numerical techniques, and applications, Rev. Mod. Phys. 91, 015002 (2019).
[23] A.B. Zamolodchikov, Irreversibility of the flux of the renormalization group in a 2D field theory, JETP Lett. 43, 730 (1986).
[24] J. Gaite and D. O’Connor, Field theory entropy, the h theorem, and the renormalization group, Phys. Rev. D 54, 5163 (1996).
[25] H. Casini and M. Huerta, A c-theorem for entanglement entropy, J. Phys. A 40, 7031 (2007).
[26] S. M. Apenko, Information theory and renormalization group flows, Physica (Amsterdam) 391A, 62 (2012).
[27] B. B. Machta, R. Chachra, M. K. Transtrum, and J. P. Sethna, Parameter space compression underlies emergent theories and predictive models, Science 342, 604 (2013).
[28] V. Balasubramanian, J.J. Heckman, and A. Maloney, Relative entropy and proximity of quantum field theories, J. High Energy Phys. 05 (2015) 104.
[29] C. Be ́ny and T. J. Osborne, The renormalization group via statistical inference, New J. Phys. 17, 083005 (2015).
[30] C. Be ́ny and T. J. Osborne, Information-geometric approach to the renormalization group, Phys. Rev. A 92, 022330 (2015).
[31] C. Be ́ny, Coarse-grained distinguishability of field interactions, Quantum 2, 67 (2018).
[32] M.I. Belghazi, A. Baratin, S. Rajeshwar, S. Ozair, Y. Bengio, A. Courville, and D. Hjelm, Mutual Information Neural Estimation (PMLR, 2018), pp. 531–540, arXiv: 1801.04062.
[33] B. Poole, S. Ozair, A. Van Den Oord, A. Alemi, and G. Tucker, On Variational Bounds of Mutual Information (PMLR, 2019), pp. 5171–5180, arXiv:1905.06922.
[34] D. Efe Gokmen, Z. Ringel, S.D. Huber, and M. Koch-Janusz, Statistical physics through the lens of real- space mutual information, arXiv:2101.11633.
[35] D. E. Gokmen, Z. Ringel, S. D. Huber, and M. Koch-Janusz, Phase diagrams with real-space mutual information neural estimation, arXiv:2103.16887.
[36] M. Koch-Janusz and Z. Ringel, Mutual information, neural networks and the renormalization group, Nat. Phys. 14, 578 (2018).
[37] P. M. Lenggenhager, D. E. Gokmen, Z. Ringel, S. D. Huber, and M. Koch-Janusz, Optimal renormalization group trans- formation from information theory, Phys. Rev. X 10, 011037 (2020).
[38] S. Hassanpour, D. Wuebben, and A. Dekorsy, Overview and investigation of algorithms for the information Bottleneck method, in Proceedings of the 11th International ITG Conference on Systems, Communications and Coding, SCC 2017 (VDE (Verlag GmbH), Berlin, 2017), pp. 1–6.
[39] A. E. Parker, T. Gedeon, and A. G. Dimitrov, Annealing and the rate distortion problem, in Proceedings of the 15th International Conference on Neural Information Process- ing Systems, NIPS02 (MIT Press, Cambridge, MA, USA, 2002), pp. 993–976.
[40] T. Gedeon, A. E. Parker, and A. .G Dimitrov, The mathematical structure of information Bottleneck methods, Entropy 14, 456 (2012).
[41] G. Chechik, A. Globerson, N. Tishby, and Y. Weiss, Information Bottleneck for Gaussian variables, in Advances in Neural Information Processing Systems, edited by S. Thrun, L. K. Saul, and B. Scholkopf (MIT Press, Cambridge, 2004), Vol. 16, pp. 1213–1220.
[42] H. A. Kramers and G. H. Wannier, Statistics of the two- dimensional ferromagnet. Part I, Phys. Rev. 60, 252 (1941).
[43] L. Onsager, Crystal statistics. I. A two-dimensional model with an order-disorder transition, Phys. Rev. 65, 117 (1944).
[44] P. Nightingale, Finite-size scaling and phenomenological renormalization, J. Appl. Phys. 53, 7927 (1982).
[45] B. Derrida and L. De Seze, Application of the phenom- enological renormalization to percolation and lattice animals in dimension 2, J. Phys. 43, 475 (1982).
[46] J. L. Cardy, Conformal invariance and universality in finitesize scaling, J. Phys. A 17, L385 (1984).
[47] J. L. Cardy, Operator content of two-dimensional conformally invariant theories, Nucl. Phys. B270, 186 (1986).
[48] See the Supplemental Material at http://link.aps.org/ supplemental/10.1103/PhysRevLett.126.240601 for further discussion and details, which includes [49–58].
[49] E. Schneidman, N. Slonim, N. Tishby, R. R. de Ruyter van Steveninck, and W. Bialek, Analyzing neural codes using the information Bottleneck method (2001), http://citeseerx
.ist.psu.edu/viewdoc/summary?doi=10.1.1.29.3263.
[50] F. Creutzig and H. Sprekeler, Predictive coding and the slowness principle: An information-theoretic approach, Neural Comput. 20, 1026 (2008).
[51] L. Buesing and W. Maass, A spiking neuron as information Bottleneck, Neural Comput. 22, 1961 (2010).
[52] N. Slonim and N. Tishby, Document clustering using word clusters via the information Bottleneck method, in Proceed- ings of the 23rd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, SIGIR ’00 (Association for Computing Machinery, New York, 2000), pp. 208–215.
[53] S. Still, W. Bialek, and L. Bottou, Geometric clustering using the information Bottleneck method, in Advances in Neural Information Processing Systems, edited by S. Thrun, L. Saul, and B. Scholkopf (MIT Press, Cambridge, 2004), Vol. 16, pp. 1165–1172.
[54] D. J. Strouse and D. J. Schwab, The information Bottleneck and geometric clustering, Neural Comput. 31, 596 (2019).
[55] F. Creutzig, A. Globerson, and N. Tishby, Past-future information bottleneck in dynamical systems, Phys. Rev. E 79, 041925 (2009).
[56] S. Still, Information Bottleneck approach to predictive inference, Entropy 16, 968 (2014).
[57] S. Agmon, E. Benger, O. Ordentlich, and N. Tishby, Critical slowing down near topological transitions in rate-distortion problems, arXiv:2103.02646.
[58] N. Slonim, The information Bottleneck: Theory and applica- tions, Ph.D. thesis, The Hebrew University of Jerusalem, 2002.
[59] A. Banerjee and Z. Ringel, Information bottleneck and Gaussian field theory (to be published).
[60] J. Zinn-Justin, Quantum Field Theory and Critical Phenomena, International Series of Monographs on Physics (Clarendon Press, Oxford, 1989).
[61] C. N. Yang and S. C. Zhang, SO4 symmetry in a Hubbard model, Mod. Phys. Lett. B 04, 759 (1990).
[62] T. Senthil, A. Vishwanath, L. Balents, S. Sachdev, and M. P. A. Fisher, Deconfined quantum critical points, Science 303, 1490 (2004).
[63] R. Bondesan and A. Lamacraft, Learning symmetries of classical integrable systems, arXiv:1906.04645.
[64] A. Nir, E. Sela, R. Beck, and Y. Bar-Sinai, Machine-learning iterative calculation of entropy for physical systems, Proc. Natl. Acad. Sci. U.S.A. 117, 30234 (2020).
集智斑图顶刊论文速递栏目上线以来,持续收录来自Nature、Science等顶刊的最新论文,追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能,每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅:

点击“阅读原文”,追踪复杂科学顶刊论文