虽然参与能量转导的生化网络已得到充分表征,但特定细胞过程的能量成本和限制仍然在很大程度上未知。特别是,细胞的能量预算是多少?能量流对细胞生命过程施加的约束和限制是什么?细胞是否在这些极限附近运行,如果是,能量限制如何影响细胞功能?物理学提供了许多工具来研究非平衡系统和定义物理极限,但将这些工具应用于细胞生物学仍然是一个挑战。近日发表于PNAS的一篇综述文章,研究者综述了「物理生物能量学」(Physical bioenergetics)这一位于非平衡物理学、能量代谢和细胞生物学交汇处的前沿领域,旨在了解细胞正在使用多少能量,它们在不同的细胞过程和相关的能量约束之间如何分配这种能量。
研究领域:生物物理,非平衡物理学,细胞能量代谢
Xingbo Yang、Matthias Heinemann、Jonathon Howard等 | 作者
赵雨亭 | 译者
刘培源 | 审校
邓一雪 | 编辑
原文地址:https://www.pnas.org/content/118/26/e2026786118
3. 开放性问题:能量通货在多大程度上限制了细胞过程?
4. 结论与展望:非平衡物理学如何阐明这些问题
本文中,研究人员回顾了最近的进展并讨论了物理生物能量学中的开放性问题和挑战。
细胞在热力学平衡之外发挥作用:它们使用代谢途径将物质和能量转化为细胞成分的构建块,并消耗吉布斯能来为细胞过程提供动力。尽管学界对生物合成和能量代谢的生物化学和细胞生物学有详细的了解[1-3],但对细胞过程的能量成本和限制知之甚少。
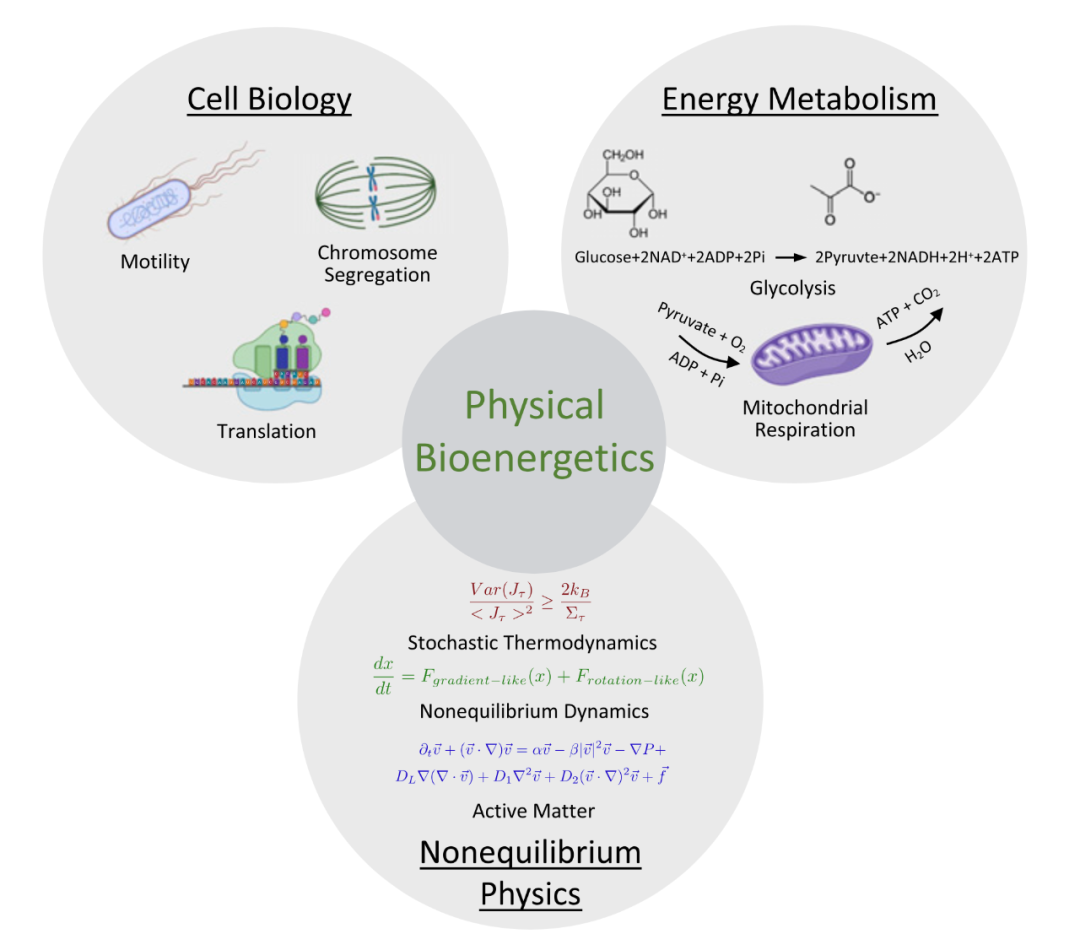
通过细胞的能量流动源于来自环境的吉布斯能的转化。能量流动的速率以能量通货为特征,可用于量化能量成本。这些能量通货还可以对细胞过程施加限制——从生长[4]分子马达的活动[5-7],到对细胞信息的促进停止[8-10]。物理生物能量学处于非平衡物理学、能量代谢和细胞生物学之间的交界处。它试图了解能量细胞正在使用多少能量,同时如何将这些能量分配到不同的细胞过程中,以及相关的能量约束(图1)。与传统的生物能量学研究[11]不同,物理生物能量学通过利用非平衡物理学的工具来研究细胞的能量成本和约束。将这些工具应用于细胞生物学面临着许多挑战。细胞内的能量通货——例如5′-三磷酸腺苷 (ATP) ——会耦合许多细胞过程,因此很难解释ATP生产和消耗中涉及的所有生化反应。虽然这一困难可以通过粗粒度(Coarse-grained)的ATP周转模型来解决,但尚不清楚如何以系统的方式对复杂的生化网络进行粗粒度的分析。活性物质物理学提供了对细胞结构涌现动力学的见解,但很少明确考虑为这些动力学提供动力的能量通货[12-16]。随机热力学为细胞过程的熵产生和能量耗散提供了下限,但不知道细胞在接近这些极限时运行的程度[17-21]。因此,物理生物能量学提出了将非平衡物理学中发展的理论和方法扩展到细胞生物学的挑战。
在本文中,研究人员将回顾和讨论物理生物能量学中三个重要的开放性问题,并展示最近的进展和新出现的挑战。首先,细胞中的能量通货是多少,如何测量它们?其次,关键细胞过程的能量成本是多少?最后,能量通货在多大程度上限制了细胞过程?研究人员将通过说明性示例解决这些问题,并强调添加物理和物理方法如何帮助回答这些问题(图1)。
图1. 物理生物能量学位于细胞生物学、能量代谢和非平衡物理学的交界,旨在揭示细胞中的能量成本和约束。它结合了来自每个领域的已有知识,以了解细胞使用多少能量、它们如何将这些能量分配到不同的细胞过程中,以及相关的能量限制。
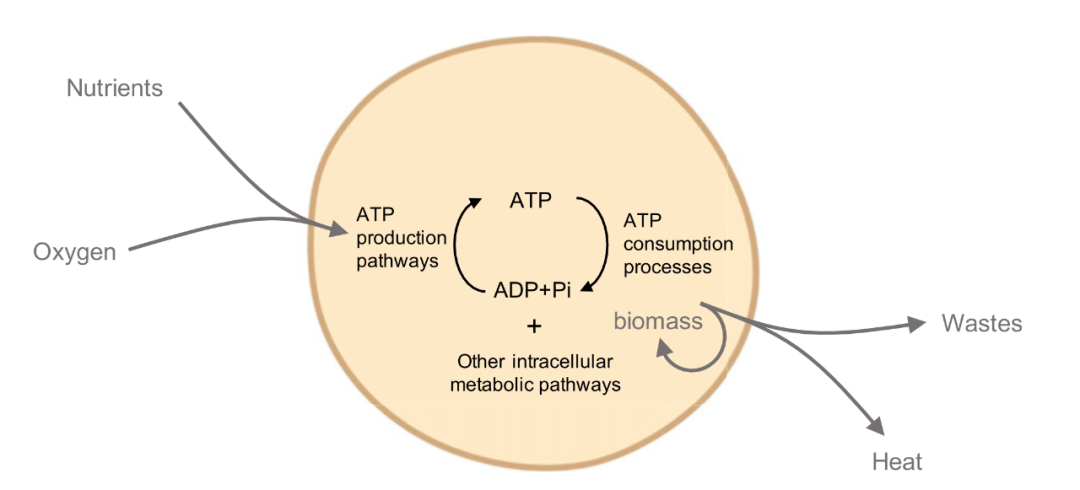
生命的定义特征之一是与环境的能量交换,其特征是能量的净流动。在细胞中,这些能量流产生于来自环境的吉布斯能的转换。这种能量在转化为生物质、热量或废物之前先转化为中间形式(例如ATP)(图2)。细胞过程的能量成本可以通过这些过程的能量流动速率或能量通货来量化[22]。能量通货还可以对细胞过程施加约束,例如通过限制细胞的生长速率[4]或诱导细胞信息处理的速度-准确性权衡[8-10]。为了揭示细胞中的能量成本和约束,测量能量通货及其变化至关重要。在本节中,研究人员将回顾在全球层面和通过特定代谢途径测量能量通货的技术,并将讨论这些技术的优势、局限性和相关挑战。
全局能量通货可以通过测量通过电位的净通量来量化,例如通过测量耗氧率或产热率。细胞内能量通货通过特定途径,包括那些产生和消耗ATP的途径,可以通过测量代谢物的通量来量化。能量通货可以是动态的——例如对于细胞进展通过细胞周期[23,24]或发育期间[25–29];或恒定——例如对于处于稳态的细胞、处在减数分裂II时停滞的卵母细胞[30]。空间效应——例如代谢物或产生能量的细胞器的扩散和运输——也会影响通过细胞的能量通货[31-34]。因为能量通货的动态对细胞能量使用的变化很敏感,它们提供了细胞能量消耗的重要指标[23,24,27,29]。
数十年的研究提供了大量关于代谢途径的详细信息,这些途径将来自环境的能量转化为可用于细胞生成的形式。尽管现有反应的酶学已被很好地表征,但通常不清楚细胞使用多少能量以及这些能量如何分配到不同的细胞器前体中。细胞全局能量通货的一个组成部分是热通量。大量研究测量了通过细胞的热通量,即细胞以通过所有细胞活动产生的热量的形式耗散能量的速率。热量的产生可以用瓦特或焦耳每秒的功率单位表示,它包含细胞中发生的所有生化反应的贡献。这种全局热通量代表了全局能量通货的焓部分,可以使用量热法进行测量[23,24,27,35–40]。对于需氧生物,全局能量通货的另一个组成部分是使用呼吸测量法测量[41–43]得到的耗氧率(oxygen consumption rate,OCR)。OCR量可以解释为在所有能量都通过呼吸获得的条件下的全球热通量,并且当与呼吸无关的氧消耗可以忽略不计时[44,45]。因为呼吸的净化学反应等价于燃烧,当满足上述条件时,OCR与释放的热量成正比,称为桑顿法则(Thornton’s rule)[46]。因此,OCR测量有时被称为间接量热法。
图2. 典型的细胞化学和能量通货示意图。能量通货代表来自环境的吉布斯能的转化率,例如从营养物质,通过细胞活动到废物、生物质或热量。灰色箭头表示通过单元的全局能量通货。整体能量通货的焓部分可以用细胞的产热率来衡量。对于有氧生物,OCR的测量可以通过桑顿规则[46]与产热率相关联。细胞内能量通货由通过特定代谢途径的通量表示,例如产生和消耗ATP的那些。
量热法和OCR的局限性在于它们都是全局测量值,具有来自许多代谢途径的贡献,这使得测量能量通货只能通过特定的细胞过程有条件地进行。这些全局测量仅提供细胞内能量通货的间接读数。要了解细胞内能量通货,测量通过特定途径的代谢通量至关重要。已应用放射性同位素14C标记等生化技术来测量此类通量,例如光合成过程中的碳通量[47]。使用质谱法进行13C代谢通量分析是用于测量细胞内通量的主要技术[48]。然而,这些技术涉及破坏性采样,限制了活细胞测量。因此,测量活细胞中的细胞内通量仍然是一个挑战。
此外,几乎所有代谢通量的测量都是在细胞群上进行的,提供了平均代谢通量的测量,掩盖了个体细胞水平的固有变化。基于显微镜的单细胞测量有助于深入了解随机细胞生长的机制[49,50]并揭示振荡代谢动力学[51],证明单细胞测量在揭示隐藏在群体水平上的代谢异质性方面的重要性。
空间效应也可能在塑造细胞内能量通货方面发挥作用。在胚胎发育过程中,糖酵解活性的梯度与细胞分化有关[52,53]。线粒体是关键的能量产生细胞器,已被观察到与细胞骨架[31]和内质网[32]相关,并显示出细胞内膜电位[54]和线粒体DNA序列[55]的异质性,这意味着潜在的存在能量流的复杂细胞内模式。糖酵解酶还与肌动蛋白细胞骨架相关联,使细胞能够将糖酵解通量与细胞机械环境的变化结合起来[56]。虽然包括ATP[57]、还原型烟酰胺腺嘌呤二核苷酸 (NADH) [58]和葡萄糖[59]在内的代谢物浓度的亚细胞分布已通过荧光显微镜[57-64]进行表征,但这仍然是一个挑战以亚细胞分辨率测量这些代谢物的通量。因此,细胞中能量通货的空间模式在很大程度上是未知的。哺乳动物卵母细胞提供了模型系统,其中可能存在能量通货的亚细胞空间模式[30,33,34]。由于它们相对较大的尺寸,由于局部ATP消耗,例如纺锤体(图3A),可能会产生大量的细胞内5′-二磷酸腺苷(ADP)梯度。已经观察到线粒体围绕着减数分裂纺锤体,这表明ATP的产生可能在空间上分布[33,34]。ATP[57]和ATP:ADP[60]生物传感器提供了强大的工具,可用于测量这些代谢物的空间梯度。通过将这些测量与ATP和ADP的理论反应扩散模型相结合,可以推断局部ATP产生和消耗的相对速率。这种方法也可能用于估计局部过程使用了多少能量。
开发能够以单细胞甚至亚细胞分辨率测量特定途径的代谢通量的新技术将有助于揭示细胞中能量通货的动态。最近在这个方向上取得了实质性进展。已经开发了一种基于乳液液滴粗化的分析方法来监测单个酵母细胞的葡萄糖摄取率[65]。拉曼光谱是一种潜在的候选方法,可以用单细胞分辨率测量养分吸收率的时空不均匀性[66]。例如,这可以使用葡萄糖类似物在细胞的静默区显示光谱峰来完成[67]。经验或基于模型的推理方法是从代谢物浓度的荧光成像中获得具有亚细胞分辨率的代谢通量的潜在方法[30,64,68]。基于NADH氧化还原反应的模型已用于从NADH的亚细胞荧光寿命成像推断线粒体代谢通量决议[30]。
总之,虽然已经开发了强大的技术来测量能量通货,但测量能量通货的动态变化和空间异质性仍然存在局限性。因此,细胞之间和细胞内的能量通货的时空动态在很大程度上仍然未知。为了弥合这一差距,需要以高时空分辨率测量能量通货的技术。
2. 开放性问题:
关键细胞过程的能量成本是多少?
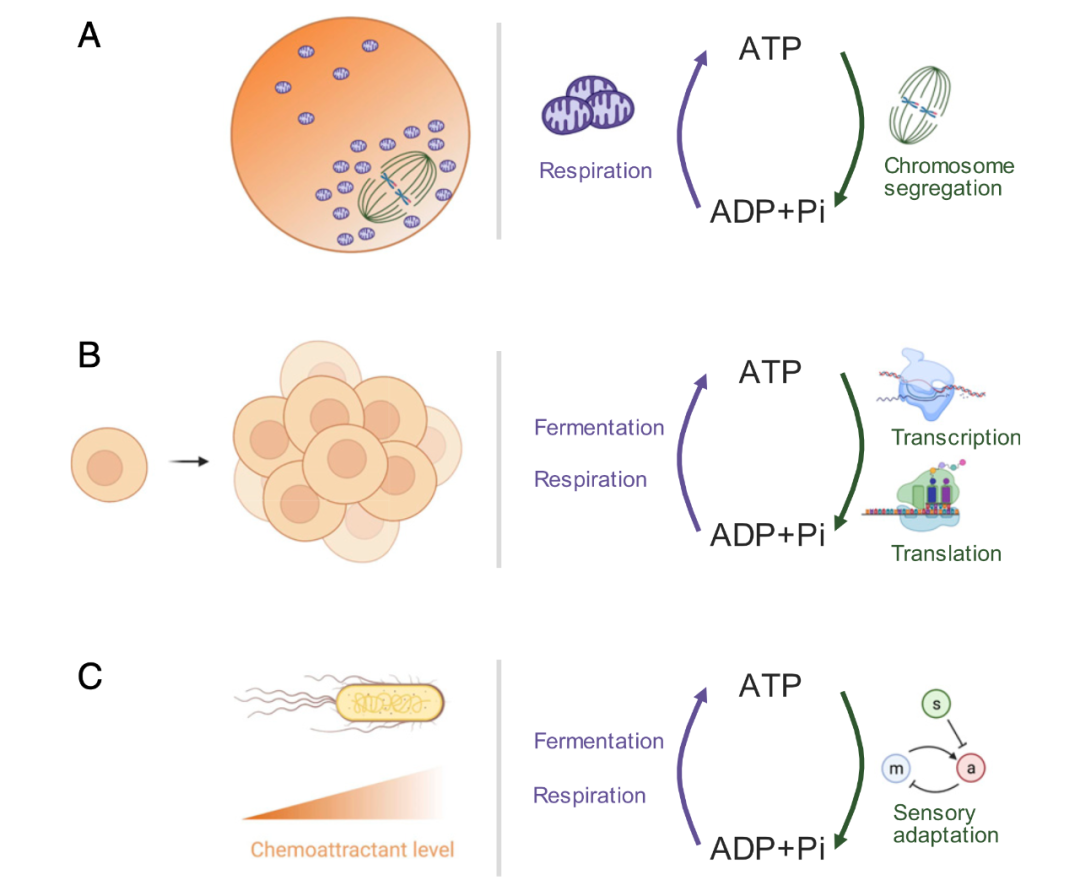
无数的细胞过程需要能量,通常以ATP的形式存在。虽然研究人员对细胞如何通过中枢代谢产生能量有相当好的了解[1,2],但特定细胞过程的能量成本却鲜为人知[69-71]。特定的细胞过程携带相关的能量成本。这些成本可以通过吉布斯能变化率来量化。量化吉布斯能变化的一种有用方法是计算细胞过程每单位时间消耗的ATP当量,即每次ATP水解的吉布斯能变化。或者,由于通过所有细胞过程的能量通货总和为细胞的全局能量通货,特定细胞过程的能量成本可以通过与该过程相关的全局能量通货的分数来量化。细胞能量成本包括生物合成[72]、信号传导[23、24、73、74]、维持化学梯度[75]、纠错[8、9]、运动性[75]、基因调控[76、77],和构建细胞结构,例如作为细胞骨架[22]。图3提供了三个有助于细胞能量收支的细胞过程示例:哺乳动物卵母细胞中的纺锤体自组织和染色体分离、生长细胞中的蛋白质合成和趋化性大肠杆菌中的感觉适应。一个公开的挑战是测量这种细胞过程的能量成本。对细胞能量的计算不仅告诉研究人员已知的过程,还告诉研究人员可能忽略的过程。例如,KaiABC系统充当蓝藻昼夜节律振荡器,通过六聚体KaiC上的一系列磷酸化反应来保持时间。虽然已知每个磷酸化-去磷酸化循环每个单体需要2个ATP,但实验测量的ATP消耗率显着每个单体16个ATP时更高。最近的一项理论研究表明,这种多余的能量并没有被简单地浪费掉——它可能负责同步KaiABC复合物之间的状态,从而实现时钟之间的全局同步[78]。
细胞过程的能量成本可以通过计算与过程相关的每个中间步骤每单位时间消耗的ATP等价物来估计。这种方法已用于通过分析生物合成途径来估算建筑成本,汇总每个中间步骤所需的ATP等价物数量[27、69、70]。这然后可以将每个步骤的ATP等价物计数与步骤速率的测量值相结合,以估计构建组件的整体能耗速率。例如,通过总结每个中间步骤(包括氨基酸合成、转录和翻译)所需的ATP等价物数量,已应用ATP等价物的计数来估计生长细胞中蛋白质合成的能量成本[69–72,79](图3B)。这种ATP等价物的计数然后可以与蛋白质合成速率的测量相结合,以估计与蛋白质合成相关的能量消耗速率。该速率可以进一步与细胞的整体能量通货进行比较,以推断相对能量蛋白质合成成本。这些估计在很大程度上依赖于了解过程中涉及的所有步骤、它们的速率以及所需的相应ATP等价物数量。对于一些特征较少的细胞过程,了解所有耦合步骤可能具有挑战性。例如,全面确定真核细胞中染色体分离的能量成本需要包括组装纺锤体、移动染色体、信号传递和纠错等能量成本(图3A)。在缺乏有关感兴趣过程的所有耦合过程的详细知识的情况下,很难估计过程的能量成本。因此,要测试ATP计数的估计值是否完全考虑了能量成本,需要直接测量。
图3.有助于细胞能量收支的细胞过程示例。(A)哺乳动物卵母细胞中的纺锤体自组织和染色体分离。(B)在生长细胞中具有转录和翻译的蛋白质合成。(C)趋化性大肠杆菌中的感官适应,a和m分别代表自适应反馈网络中的输入、输出和控制器[10]。
一种直接测量过程能量成本的方法是通过过程抑制。假设抑制一个目标过程不影响其他细胞过程的活动,目标过程的能量成本可以被测量为当目标过程被抑制时使用呼吸测量法或量热法的全局能量通货的变化[22]。如何-一直以来,抑制实验总是具有脱靶效应的潜力,并且可以改变与目标相关的其他过程的活性[80]。由于全局能量通货的变化反映了所有受影响过程的变化,目标过程与其他细胞过程之间的耦合可能会使此类测量的解释复杂化。例如,抑制代表细胞ATP消耗率很大一部分的过程可能会改变ATP浓度,这反过来可能会改变其他ATP消耗途径的活动。在这种情况下,测得的全局能量通货变化除了来自受抑制过程的贡献外,还可能包括来自这些下游效应的额外贡献。此外,全局能量通货可能不是由ATP使用者强加的能量需求唯一决定的,还取决于线粒体中ATP合成和质子泄漏的速率[81]。因此,需要了解抑制作用如何调节ATP合成和质子泄漏,以估计此类实验的能量成本。需要代谢控制模型来理解ATP合成、质子泄漏和ATP酶的耦合[45]。为了确定与给定细胞过程相关的真实能量成本,需要一种组合方法,其中能量成本是使用ATP等价物的计数和测量特定过程抑制后全局能量通货的变化来测量的[80]。
测量发育过程中全局能量通货的变化也提供了有关细胞过程能量消耗的信息。例如,量热法已被用于观察在斑马鱼[24]和非洲爪蟾[23]胚胎发育过程中,由于细胞周期信号传导,胚胎产生的热量包含与细胞周期同步振荡的成分。了解胚胎发育过程中哪些生理变化对能量通货的动态有贡献仍然是一个挑战[27,29,82-84]。
上面考虑的能量成本代表直接成本,定义为给定细胞过程使用的ATP等价物的数量。在某些情况下,例如对于产生生物质的过程,间接机会成本可能是相关的。机会成本代表了如果代谢前体或还原中间体被用于生成ATP而不是生物质,本可以生成ATP[70]。虽然机会成本不是直接的能量成本,但它们可能对进化适应性产生影响,特别是在碳有限的情况下,因此将碳转移到生物质的后果更为严重。了解如何将能量成本与健康成本联系起来是一个重要的开放性问题,它将物理生物能量学与进化细胞生物学联系起来[69,70,85-88]。
总体而言,虽然在估计细胞过程的能量成本方面存在有希望的工作[22,69,70,78],但细胞的能量预算在很大程度上仍未得到探索。从ATP计数和过程抑制估计能量成本存在挑战。克服这些挑战需要了解与感兴趣的过程相关的中间步骤,以及ATP生产和ATP消耗之间的耦合。
3. 开放性问题:
能量通货在多大程度上限制了细胞过程?
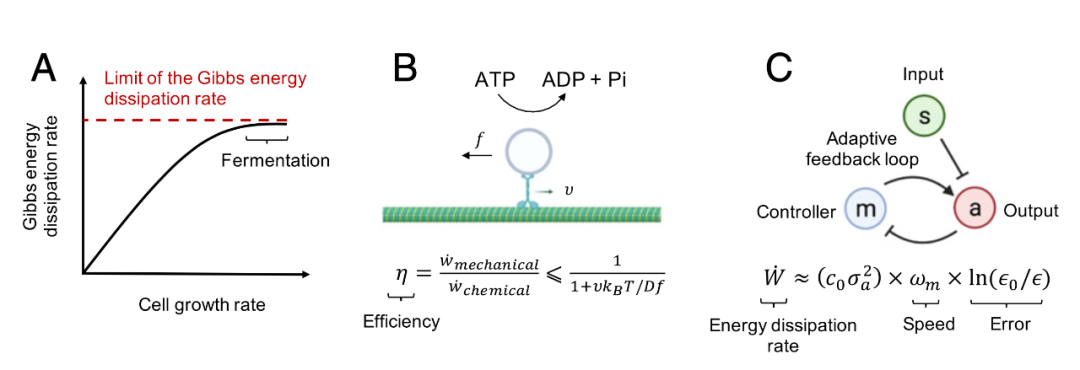
细胞过程由吉布斯能的耗散提供动力,能量耗散率可以对细胞过程施加限制。这些限制体现在细胞生长速率的限制[4](图4A)、分子马达的效率[5-7](图4B)以及细胞信息处理速度和准确性之间的权衡[8–10](图4C)。在本节中,研究人员将详细讨论这些示例,并演示如何应用非平衡物理学中的工具来理解能量约束。
吉布斯能耗散率的内在限制可能对细胞生长率施加限制。最近有人建议,从呼吸到发酵的转变在高葡萄糖摄取率是由细胞吉布斯能耗散率的上限引起的,最大细胞生长率由该限制决定[4] (图4A)。这种现象的另一种解释包括电子传输链酶在细胞膜中达到饱和浓度[89,90]和有效的蛋白质组分配[91]。协调这些不同的解释仍然是一个挑战。
随机热力学理论已被用于预测分子马达热力学效率的限制。热力学效率定义为有用的能量耗散速度,例如机械功率,除以总能量耗散率,例如来自ATP水解的能量耗散率。热力学不确定性关系表明能量耗散限制非平衡系统稳态时的电流波动[19,92-94]。将此关系应用于抵抗外力或扭矩的分子马达,例如在粘性环境中移动货物,可以预测热力学效率的通用上限[95](图4B)。
Harada-Sasa等式将能量耗散率与波动响应关系的违反程度相关联,已被用于估计单个驱动蛋白电机的效率为20%[5]。相比之下,旋转电机F1-ATPase已被建议以接近100%的效率运行[6,7]。对这两种电机效率之间形成鲜明对比的候选解释调用了它们动力学的可逆性[5]。虽然两个电机在向前迈进时都会消耗ATP,但F1-ATPase可以在向后旋转时合成ATP。因此,与驱动蛋白相反,这些后退步骤的能量是可以守恒的。了解运动效率的进化压力是一个活跃的研究领域[96]。
非平衡物理理论也预测了受能量耗散率约束的生化回路中的权衡。在DNA复制等过程中,核苷酸提供的吉布斯能在复制速度、复制精度、和能量耗散[9]。动力学校对是一种以能量消耗为代价的生物化学反应纠错机制,对于许多细胞过程的质量控制和准确性很重要[8,97]。跟踪能量消耗并了解能量耗散如何有助于提高细胞中信息处理的灵敏度和速度和/或准确性,既是一项实验挑战,也是一项理论挑战[8,10,74,76,77,98-103]。关于生化网络中能量-性能权衡的新见解使生物网络的有用设计原则得以识别,以有效地实现其目标功能[78、104、105]。例如,在大肠杆菌的化学感应适应过程中,Gibbs能量耗散是必要的,必须消耗能量以适应化学引诱物浓度的变化,同时保持化学感受器的敏感性(图3C)。反馈网络的粗粒度模型预测了感官适应中的一般能量-速度-准确度权衡关系。该模型在不影响饥饿大肠杆菌的适应精度的情况下预测了适应速度的降低,这已在实验中得到证实[10] (图4C)。
图4. 能量通货对细胞过程施加的限制和约束示例。(A):已经提出了用于生长大肠杆菌和酵母的Gibbs能量耗散率的限制。在这个模型中,当Gibbs能量耗散率达到接近此限制,最大细胞生长速率由此限制决定[4]。(B):热力学不确定性关系预测分子马达能量效率的上限[95]。v、f、D、kB和T分别代表速度、力、扩散常数、玻尔兹曼常数和温度。(C):粗粒度自适应反馈模型预测感官适应期间的能量-速度-准确度权衡,包括细菌趋化性、酵母渗透传感、嗅觉适应和视紫质适应[10]。c0和ε0依赖于系统常数,σa2是活动“a”波动的方差,ωm是适应速度,ε是适应误差。
这些例子强调了能量约束在理解细胞生长速率的极限、分子马达的效率和细胞信息处理中的速度-准确度权衡方面的作用,同时提出了更多问题。能量约束在多大程度上存在对于其他细胞过程?如果给定过程存在能量约束,细胞是否在该极限附近运行?解决这些问题需要结合定量测量和基于非平衡物理学的新理论的发展。非平衡动力学[106-109]和随机热力学[17-21]的最新进展为研究非平衡过程和定义物理极限提供了工具。这些工具有助于量化非平衡系统中的熵产生[110-115]、能量耗散[18、19、92、116、117]、功[118、119]和自由能转换[120]。将热力学原理应用于代谢网络导致发现了对代谢通量的能量限制[4,121–123]。已经开发了新的实验和理论方法,通过量化详细平衡的破坏[124-126]和不可逆性[127,128]来识别生物系统中的非平衡动力学。波动-耗散关系的违反也被用于量化单次能量耗散。量化分子水平的单次能量消耗[5]。将这些理论应用于细胞生物学以理解能量耗散和细胞功能之间的相互关系仍然是一个挑战[129-136]。
物理生物能量学旨在揭示细胞中的能量成本和约束,利用非平衡物理学中的工具并将其应用于细胞生物学和能量方面的开放性问题代谢。物理生物能量学的中心主题是了解细胞使用多少能量,它们如何将这些能量分配到不同的细胞过程中,以及相关的能量性约束。正在开发新技术以研究具有单细胞和亚细胞分辨率的能量通货[30,57,59–64,67,137],这使得研究能量通货与亚细胞过程之间的相关性成为可能。非平衡物理学提供了新的工具来解释这些测量的动力学[106-108]、熵产生[21、111、112、115]、能量耗散[18、19、92、116、117]及其与涌现动力学的相关性细胞结构[13、14、124、126、128]。
尽管最近取得了这些进展,但物理生物能量学仍然存在挑战和机遇。实验家和理论家面临着理解细胞如何利用能量来构建细胞结构和驱动细胞过程的挑战。研究人员如何最有效地定义和测量时空能量通货,并将其与细胞和亚细胞尺度上的效率、焓、熵和吉布斯能耗散等物理量联系起来?研究人员是否对细胞过程的生物化学和速率有足够的定量知识,以便计算它们在细胞能量预算内的能量使用和大小?能量耗散率对细胞过程有哪些限制和权衡,以及对细胞功能产生的后果是什么?
非平衡物理学与来自生物化学和细胞生物学的方法相结合,提供了有望解决这些问题的其他工具。将这些工具应用于细胞系统对实验家和理论家来说都是一个开放的挑战,需要扩展现有的物理理论并开发新的实验方法。物理生物能量学为这些理论提供了一个试验场,并将为非平衡物理学的发展提供信息例如,将随机热力学应用于分子马达已经揭示了其效率的限制[5-7](图4B),但目前尚不清楚马达是否在细胞中的预测极限附近运行。活性物质物理学有助于为由能量通货产生的细胞结构的丰富时空动力学提供定量框架,但很少直接研究能量通货本身。由于细胞中的能量通货并不总是恒定的,因此考虑能量通货动力学和细胞结构动力学之间的相互作用很重要。(图3A)[12、138-140]。
建模细胞系统的另一个基本挑战在于系统地开发复杂代谢网络的现象学和粗粒度模型。通过结合所有已知的相关代谢途径,经常构建计算模型来研究代谢网络[141-143]。虽然这些模型为代谢提供了许多重要的见解,但它们通常依赖于大量参数,这些参数可能高度依赖上下文并且难以在体内测量。粗粒度和现象学模型是建模的潜在有用工具有效参数很少的代谢网络。这种方法已被证明在许多领域都很有用。例如,主动-在物质物理学中,细胞骨架动力学可以通过场理论使用很少的现象学参数很好地描述,而无需详细了解系统的微观特性[12,13,15,16,144,145]。还开发了粗粒度详细微观模型的技术,以获得这些系统的流体动力学模型[146-149]。这种粗粒度建模方法已开始应用于建模细胞能量流[30,89,91,150–154]。这种粗粒度的现象学定律可潜在地用于解释由OCR[28,43]和产热率[23,24]测量的全局能量通货的变化,并提供对细胞能量使用的见解。
研究人员怎么知道自己是否完美地回答了这个角度提出的开放性问题?归结为使用理论模型进行定量预测并在细胞中进行实验测试。例如,研究人员能否预测特定细胞过程的能量成本?研究人员能预测细胞结构的动力学行为吗?研究人员能预测细胞过程的相关能量极限吗?研究人员能否整合这些信息来对细胞特征的演变做出可测试的预测?总体而言,物理生物能量学为跨学科的科学家提供了一个机会,可以将最近的实验和理论进展结合起来,并解决从这个新视角产生的新问题和挑战。
1 J. G. Salway, Metabolism at a Glance (John Wiley & Sons, 2017).
2 D. White, J. T. Drummond, C. Fuqua, The Physiology and Biochemistry of Prokaryotes (Oxford University Press, New York, 2012).
3 B. Alberts et al., Molecular Biology of the Cell (Garland Science, 5th Ed., 2007).
4 B. Niebel, S. Leupold, M. Heinemann, An upper limit on Gibbs energy dissipation governs cellular metabolism. Nat. Metab. 1, 125–132 (2019).
5 T. Ariga, M. Tomishige, D. Mizuno, Nonequilibrium energetics of molecular motor kinesin. Phys. Rev. Lett. 121, 218101 (2018).
6 S. Toyabe et al., Nonequilibrium energetics of a single F1-ATPase molecule. Phys. Rev. Lett. 104, 198103 (2010).
7 S. Toyabe, T. Watanabe-Nakayama, T. Okamoto, S. Kudo, E. Muneyuki, Thermodynamic efficiency and mechanochemical coupling of F1-ATPase. Proc. Natl. Acad. Sci. U.S.A. 108, 17951–17956 (2011).
8 J. J. Hopfield, Kinetic proofreading: A new mechanism for reducing errors in biosynthetic processes requiring high specificity. Proc. Natl. Acad. Sci. U.S.A. 71, 4135–4139 (1974).
9 P. Sartori, S. Pigolotti, Thermodynamics of error correction. Phys. Rev. X 5, 041039 (2015).
10 G. Lan, P. Sartori, S. Neumann, V. Sourjik, Y. Tu, The energy-speed-accuracy tradeoff in sensory adaptation. Nat. Phys. 8, 422–428 (2012).
11 D. G. Nicholls, S. J. Ferguson, Bioenergetics (Academic Press, 2013).
12 J. Brugu ´es, D. Needleman, Physical basis of spindle self-organization. Proc. Natl. Acad. Sci. U.S.A. 111, 18496–18500 (2014). Yang et al. Physical bioenergetics: Energy fluxes, budgets, and constraints in cells https://doi.org/10.1073/pnas.2026786118 Downloaded at Institute of Automation on July 18, 2021
13 M. C. Marchetti et al., Hydrodynamics of soft active matter. Rev. Mod. Phys. 85, 1143–1189 (2013).
14 D. Needleman, Z. Dogic, Active matter at the interface between materials science and cell biology. Nat. Rev. Mater. 2, 17048 (2017).
15 J. Prost, F. Jülicher, J. F. Joanny, Active gel physics. Nat. Phys. 11, 111–117 (2015).
16 P. Ronceray, C. P. Broedersz, M. Lenz, Fiber networks amplify active stress. Proc. Natl. Acad. Sci. U.S.A. 113, 2827–2832 (2016).
17 G. Falasco, M. Esposito, Dissipation-time uncertainty relation. Phys. Rev. Lett. 125, 120604 (2020).
18 T. R. Gingrich, G. M. Rotskoff, J. M. Horowitz, Inferring dissipation from current fluctuations. J. Phys. A Math. Theor. 50, 184004–184024 (2017).
19 J. M. Horowitz, T. R. Gingrich, Thermodynamic uncertainty relations constrain non-equilibrium fluctuations. Nat. Phys. 16, 15–20 (2020).
20 R. Rao, M. Esposito, Conservation laws shape dissipation. New J. Phys. 20, 023007–023032 (2018).
21 U. Seifert, Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 75, 126001–126059 (2012).
22 S. A. Mookerjee, A. A. Gerencser, D. G. Nicholls, M. D. Brand, Quantifying intracellular rates of glycolytic and oxidative ATP production and consumption using extracellular flux measurements. J. Biol. Chem. 292, 7189–7207 (2017).
23 Y. Nagano, K. L. Ode, Temperature-independent energy expenditure in early development of the African clawed frog Xenopus laevis. Phys. Biol. 11, 046008–046013 (2014).
24 J. Rodenfels, K. M. Neugebauer, J. Howard, Heat oscillations driven by the embryonic cell cycle reveal the energetic costs of signaling. Dev. Cell 48, 646–658.e6 (2019).
25 J. M. Tennessen, K. D. Baker, G. Lam, J. Evans, C. S. Thummel, The Drosophila estrogen-related receptor directs a metabolic switch that supports developmental growth. Cell Metab. 13, 139–148 (2011).
26 R. L. Krisher, R. S. Prather, A role for the Warburg effect in preimplantation embryo development: Metabolic modification to support rapid cell proliferation. Mol. Reprod. Dev. 79, 311–320 (2012).
27 Y. Song et al., Energy budget of Drosophila embryogenesis. Curr. Biol. 29, R566–R567 (2019).
28 R. J. Chason, J. Csokmay, J. H. Segars, A. H. DeCherney, D. R. Armant, Environmental and epigenetic effects upon preimplantation embryo metabolism and development. Trends Endocrinol. Metab. 22, 412–420 (2011).
29 J. Rodenfels et al., Contribution of increasing plasma membrane to the energetic cost of early zebrafish embryogenesis. Mol. Biol. Cell 31, 520–526 (2020).
30 X. Yang, D. J. Needleman, Coarse-grained model of mitochondrial metabolism enables subcellular flux inference from fluorescence lifetime imaging of NADH. bioRxiv [Preprint] (2020). https://doi.org/10.1101/2020.11.20.392225 (Accessed 7 April 2021).
31 E. J. Lawrence, E. Boucher, C. A. Mandato, Mitochondria-cytoskeleton associations in mammalian cytokinesis. Cell Div. 11, 3 (2016).
32 R. Dumollard et al., Sperm-triggered [Ca2+] oscillations and Ca2+ homeostasis in the mouse egg have an absolute requirement for mitochondrial ATP production. Development 131, 3057–3067 (2004).
33 X.-H. Wang, S. Yin, X.-H. Ou, S.-M. Luo, Increase of mitochondria surrounding spindle causes mouse oocytes arrested at metaphase I stage. Biochem. Biophys. Res. Commun. 527, 1043–1049 (2020).
34 X. Duan et al., Dynamic organelle distribution initiates actin-based spindle migration in mouse oocytes. Nat. Commun. 11, 277 (2020).
35 L. C. M. Auberson, T. Kanbier, U. von Stockar, Monitoring synchronized oscillating yeast cultures by calorimetry. J. Biotechnol. 29, 205–215 (1993).
36 P. J. Foster, M. Razo-Mejia, R. Phillips, Measuring the energetic costs of embryonic development. Dev. Cell 48, 591–592 (2019).
37 S. Hur, R. Mittapally, S. Yadlapalli, P. Reddy, E. Meyhofer, Sub-nanowatt resolution direct calorimetry for probing real-time metabolic activity of individual C.elegans worms. Nat. Commun. 11, 2983 (2020).
38 R. B. Kemp, Microcalorimetric studies of tissue cells and bacteria. Pestic. Sci. 6, 311–325 (1975).
39 T. Maskow, S. Paufler, What does calorimetry and thermodynamics of living cells tell us? Methods 76, 3–10 (2015).
40 A. Thommen et al., Body size-dependent energy storage causes Kleiber’s law scaling of the metabolic rate in planarians. eLife 8, e38187 (2019).
41 D. A. Ferrick, A. Neilson, C. Beeson, Advances in measuring cellular bioenergetics using extracellular flux. Drug Discov. Today 13, 268–274 (2008).
42 E. Gnaiger, G. M ´endez, S. C. Hand, High phosphorylation efficiency and depression of uncoupled respiration in mitochondria under hypoxia. Proc. Natl. Acad. Sci. U.S.A. 97, 11080–11085 (2000).
43 F. D. Houghton, J. G. Thompson, C. J. Kennedy, H. J. Leese, Oxygen consumption and energy metabolism of the early mouse embryo. Mol. Reprod. Dev. 44, 476–485 (1996).
44 P. M. Herst, M. V. Berridge, Cell surface oxygen consumption: A major contributor to cellular oxygen consumption in glycolytic cancer cell lines. Biochim. Biophys. Acta 1767, 170–177 (2007).
45 D. F. Rolfe, G. C. Brown, Cellular energy utilization and molecular origin of standard metabolic rate in mammals. Physiol. Rev. 77, 731–758 (1997).
46 W. M. Thornton, XV. The relation of oxygen to the heat of combustion of organic compounds. Lond. Edinb. Dublin Philos. Mag. J. Sci. 33, 196–203 (1917).
47 M. Calvin, The path of carbon in photosynthesis (1961). https://www.nobelprize.org/prizes/chemistry/1961/calvin/lecture/. Accessed 8 March 2021.
48 W. Wiechert, 13C metabolic flux analysis. Metab. Eng. 3, 195–206 (2001).
49 S. Iyer-Biswas et al., Scaling laws governing stochastic growth and division of single bacterial cells. Proc. Natl. Acad. Sci. U.S.A. 111, 15912–15917 (2014).
50 F. Si et al., Mechanistic origin of cell-size control and homeostasis in bacteria. Curr. Biol. 29, 1760–1770.e7 (2019).
51 A. Papagiannakis, B. Niebel, E. C. Wit, M. Heinemann, Autonomous metabolic oscillations robustly gate the early and late cell cycle. Mol. Cell 65, 285–295 (2017).
52 V. Bulusu et al., Spatiotemporal analysis of a glycolytic activity gradient linked to mouse embryo mesoderm development. Dev. Cell 40, 331–341.e4 (2017).
53 M. Oginuma et al., A gradient of glycolytic activity coordinates FGF and wnt signaling during elongation of the body Axis in amniote embryos. Dev. Cell 40, 342–353.e10 (2017).
54 S. T. Smiley et al., Intracellular heterogeneity in mitochondrial membrane potentials revealed by a J-aggregate-forming lipophilic cation JC-1. Proc. Natl. Acad. Sci. U.S.A. 88, 3671–3675 (1991).
55 J. Morris et al., Pervasive within-mitochondrion single-nucleotide variant heteroplasmy as revealed by single-mitochondrion sequencing. Cell Rep. 21, 2706–2713 (2017).
56 J. S. Park et al., Mechanical regulation of glycolysis via cytoskeleton architecture. Nature 578, 621–626 (2020).
57 H. Imamura et al., Visualization of ATP levels inside single living cells with fluorescence resonance energy transfer-based genetically encoded indicators. Proc. Natl. Acad. Sci. U.S.A. 106, 15651–15656 (2009).
58 M. C. Skala et al., In vivo multiphoton fluorescence lifetime imaging of protein-bound and free nicotinamide adenine dinucleotide in normal and precancerous epithelia. J. Biomed. Opt. 12, 024014 (2007).
59 C. M. Daz-Garca et al., Quantitative in vivo imaging of neuronal glucose concentrations with a genetically encoded fluorescence lifetime sensor. J. Neurosci. Res. 97, 946–960 (2019).
60 J. Berg, Y. P. Hung, G. Yellen, A genetically encoded fluorescent reporter of ATP:ADP ratio. Nat. Methods 6, 161–166 (2009).
61 A. A. Heikal, Intracellular coenzymes as natural biomarkers for metabolic activities and mitochondrial anomalies. Biomarkers Med. 4, 241–263 (2010).
62 Y. P. Hung, J. G. Albeck, M. Tantama, G. Yellen, Imaging cytosolic NADH-NAD(+) redox state with a genetically encoded fluorescent biosensor. Cell Metab. 14, 545–554 (2011).
63 J. R. Lakowicz, H. Szmacinski, K. Nowaczyk, M. L. Johnson, Fluorescence lifetime imaging of free and protein-bound NADH. Proc. Natl. Acad. Sci. U.S.A. 89, 1271–1275 (1992).
64 A. San Martn et al., Imaging mitochondrial flux in single cells with a FRET sensor for pyruvate. PLoS One 9, e85780 (2014).
65 L. Boitard et al., Monitoring single-cell bioenergetics via the coarsening of emulsion droplets. Proc. Natl. Acad. Sci. U.S.A. 109, 7181–7186 (2012). Yang et al. https://doi.org/10.1073/pnas.2026786118 Physical bioenergetics: Energy fluxes, budgets, and constraints in cells Downloaded at Institute of Automation on July 18, 2021
66 S. Oh et al., In situ measurement of absolute concentrations by normalized Raman imaging. bioRxiv [Preprint] (2019). https://doi.org/10.1101/629543 (Accessed 13 October 2020).
67 F. Hu et al., Vibrational imaging of glucose uptake activity in live cells and tissues by stimulated Raman scattering. Angew. Chem. Int. Ed. Engl. 54, 9821–9825 (2015).
68 F. Monteiro et al., Measuring glycolytic flux in single yeast cells with an orthogonal synthetic biosensor. Mol. Syst. Biol. 15, e9071 (2019).
69 M. Lynch, G. K. Marinov, The bioenergetic costs of a gene. Proc. Natl. Acad. Sci. U.S.A. 112, 15690–15695 (2015).
70 G. Mahmoudabadi, R. Phillips, M. Lynch, R. Milo, Defining the energetic costs of cellular structures. bioRxiv [Preprint] (2019). https://doi.org/10.1101/666040 (Accessed 31 December 2019).
71 A. H. Stouthamer, A theoretical study on the amount of ATP required for synthesis of microbial cell material. Antonie van Leeuwenhoek 39, 545–565 (1973).
72 R. Phillips, R. Milo, A feeling for the numbers in biology. Proc. Natl. Acad. Sci. U.S.A. 106, 21465–21471 (2009).
73 T.-L. Wang, B. Kuznets-Speck, J. Broderick, M. Hinczewski, The price of a bit: Energetic costs and the evolution of cellular signaling. bioRxiv [Preprint] (2020). https://doi.org/10.1101/2020.10.06.327700 (Accessed 28 March 2021).
74 P. Mehta, D. J. Schwab, Energetic costs of cellular computation. Proc. Natl. Acad. Sci. U.S.A. 109, 17978–17982 (2012).
75 R. Milo, R. Phillips, Cell Biology by the Numbers (Garland Science, 2016).
76 J. Estrada, F. Wong, A. DePace, J. Gunawardena, Information integration and energy expenditure in gene regulation. Cell 166, 234–244 (2016).
77 F. Wong, J. Gunawardena, Gene regulation in and out of equilibrium. Annu. Rev. Biophys. 49, 199–226 (2020).
78 D. Zhang, Y. Cao, Q. Ouyang, Y. Tu, The energy cost and optimal design for synchronization of coupled molecular oscillators. Nat. Phys. 16, 95–100 (2020).
79 R. Phillips, J. Kondev, J. Theriot, Physical Biology of the Cell (Garland Science, New York, 2008).
80 W. Wieser, G. Krumschnabel, Hierarchies of ATP-consuming processes: Direct compared with indirect measurements, and comparative aspects. Biochem. J. 355, 389–395 (2001).
81 G. C. Brown, Control of respiration and ATP synthesis in mammalian mitochondria and cells. Biochem. J. 284, 1–13 (1992).
82 H. Miyazawa, A. Aulehla, Revisiting the role of metabolism during development. Development 145, dev131110 (2018).
83 Y. Song, S. Y. Shvartsman, Chemical embryology redux: Metabolic control of development. Trends Genet. 36, 577–586 (2020).
84 F. Chi, M. S. Sharpley, R. Nagaraj, S. S. Roy, U. Banerjee, Glycolysis-independent glucose metabolism distinguishes TE from ICM fate during mammalian embryogenesis. Dev. Cell 53, 9–26.e4 (2020).
85 E. Ilker, M. Hinczewski, Modeling the growth of organisms validates a general relation between metabolic costs and natural selection. Phys. Rev. Lett. 122, 238101 (2019).
86 B. Ni, R. Colin, H. Link, R. G. Endres, V. Sourjik, Growth-rate dependent resource investment in bacterial motile behavior quantitatively follows potential benefit of chemotaxis. Proc. Natl. Acad. Sci. U.S.A. 117, 595–601 (2020).
87 M. Lynch, B. Trickovic, A theoretical framework for evolutionary cell biology. J. Mol. Biol. 432, 1861–1879 (2020).
88 L. A. Hoekstra, K. L. Montooth, Inducing extra copies of the Hsp70 gene in Drosophila melanogaster increases energetic demand. BMC Evol. Biol. 13, 68 (2013).
89 M. Szenk, K. A. Dill, A. M. R. de Graff, Why do fast-growing bacteria enter overflow metabolism? testing the membrane real estate hypothesis. Cell Syst. 5, 95–104 (2017).
90 K. Zhuang, G. N. Vemuri, R. Mahadevan, Economics of membrane occupancy and respiro-fermentation. Mol. Syst. Biol. 7, 500 (2011).
91 M. Basan et al., Overflow metabolism in Escherichia coli results from efficient proteome allocation. Nature 528, 99–104 (2015).
92 J. Li, J. M. Horowitz, T. R. Gingrich, N. Fakhri, Quantifying dissipation using fluctuating currents. Nat. Commun. 10, 1666 (2019).
93 T. R. Gingrich, J. M. Horowitz, N. Perunov, J. L. England, Dissipation bounds all steady-state current fluctuations. Phys. Rev. Lett. 116, 120601–120605 (2016).
94 A. C. Barato, U. Seifert, Thermodynamic uncertainty relation for biomolecular processes. Phys. Rev. Lett. 114, 158101 (2015).
95 P. Pietzonka, A. C. Barato, U. Seifert, Universal bound on the efficiency of molecular motors. J. Stat. Mech. 2016, 124004 (2016).
96 J. A. Wagoner, K. A. Dill, Opposing pressures of speed and efficiency guide the evolution of molecular machines. Mol. Biol. Evol. 36, 2813–2822 (2019).
97 J. Ninio, Kinetic amplification of enzyme discrimination. Biochimie 57, 587–595 (1975).
98 G. Shin, J. Wang, The role of energy cost on accuracy, sensitivity, specificity, speed and adaptation of T cell foreign and self recognition. Phys. Chem. Chem. Phys. 23, 2860–2872 (2021).
99 A. C. Barato, D. Hartich, U. Seifert, Efficiency of cellular information processing. New J. Phys. 16, 103024 (2014).
100 J. Park et al., Dissecting the sharp response of a canonical developmental enhancer reveals multiple sources of cooperativity. eLife 8, e41266 (2019).
101 Y. Tu, The nonequilibrium mechanism for ultrasensitivity in a biological switch: Sensing by Maxwell’s demons. Proc. Natl. Acad. Sci. U.S.A. 105, 11737–11741 (2008).
102 G. Lan, Y. Tu, The cost of sensitive response and accurate adaptation in networks with an incoherent type-1 feed-forward loop. J. R. Soc. Interface 10, 20130489 (2013).
103 Y. Cao, H. Wang, Q. Ouyang, Y. Tu, The free-energy cost of accurate biochemical oscillations. Nat. Phys. 11, 772–778 (2015).
104 C. Fei, Y. Cao, Q. Ouyang, Y. Tu, Design principles for enhancing phase sensitivity and suppressing phase fluctuations simultaneously in biochemical oscillatory systems. Nat. Commun. 9, 1434 (2018).
105 Y. Tu, Y. Cao, Design principles and optimal performance for molecular motors under realistic constraints. Phys. Rev. E 97, 022403 (2018).
106 X. Fang, J. Wang, Nonequilibrium thermodynamics in cell biology: Extending equilibrium formalism to cover living systems. Annu. Rev. Biophys. 49, 227–246 (2020).
107 X. Fang, K. Kruse, T. Lu, J. Wang, Nonequilibrium physics in biology. Rev. Mod. Phys. 91, 045004 (2019).
108 J. Wang, Landscape and flux theory of non-equilibrium dynamical systems with application to biology. Adv. Phys. 64, 1–137 (2015).
109 J. Wang, L. Xu, E. Wang, Potential landscape and flux framework of nonequilibrium networks: Robustness, dissipation, and coherence of biochemical oscillations. Proc. Natl. Acad. Sci. U.S.A. 105, 12271–12276 (2008).
110 H. Ge, H. Qian, Physical origins of entropy production, free energy dissipation, and their mathematical representations. Phys. Rev. E 81, 051133 (2010).
111 C. Nardini et al., Entropy production in field theories without time-reversal symmetry: Quantifying the non-equilibrium character of active matter. Phys. Rev. X 7, 021007–021020 (2017).
112 J. M. R. Parrondo, J. M. Horowitz, T. Sagawa, Thermodynamics of information. Nat. Phys. 11, 131–139 (2015).
113 H. Qian, D. A. Beard, Thermodynamics of stoichiometric biochemical networks in living systems far from equilibrium. Biophys. Chem. 114, 213–220 (2005).
114 U. Seifert, Entropy production along a stochastic trajectory and an integral fluctuation theorem. Phys. Rev. Lett. 95, 040602 (2005).
115 S. Shankar, M. C. Marchetti, Hidden entropy production and work fluctuations in an ideal active gas. Phys. Rev. E 98, 020604 (2018).
116 E. Fodor et al., Nonequilibrium dissipation in living oocytes. EPL 116, 30008 (2016).
117 T. Harada, S. Sasa, Equality connecting energy dissipation with a violation of the fluctuation-response relation. Phys. Rev. Lett. 95, 130602–130604 (2005).
118 C. Jarzynski, Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 78, 2690–2693 (1997).
119 P. Pietzonka, E. Fodor, C. Lohrmann, M. E. Cates, U. Seifert, Autonomous engines driven by active matter: Energetics and design principles. Phys. Rev. X 9, 041032 (2019).
120 T. L. Hill, Free Energy Transduction and Biochemical Cycle Kinetics (Springer, 2005).
121 D. A. Beard, S. D. Liang, H. Qian, Energy balance for analysis of complex metabolic networks. Biophys. J. 83, 79–86 (2002).
122 D. A. Beard, E. Babson, E. Curtis, H. Qian, Thermodynamic constraints for biochemical networks. J. Theor. Biol. 228, 327–333 (2004).
123 J. O. Park et al., Near-equilibrium glycolysis supports metabolic homeostasis and energy yield. Nat. Chem. Biol. 15, 1001–1008 (2019). Yang et al. Physical bioenergetics: Energy fluxes, budgets, and constraints in cells https://doi.org/10.1073/pnas.2026786118 Downloaded at Institute of Automation on July 18, 2021
124 C. Battle et al., Broken detailed balance at mesoscopic scales in active biological systems. Science 352, 604–607 (2016).
125 Q. Liu, J. Wang, Quantifying the flux as the driving force for nonequilibrium dynamics and thermodynamics in non-Michaelis-Menten enzyme kinetics. Proc. Natl. Acad. Sci. U.S.A. 117, 923–930 (2020).
126 J. Gladrow, N. Fakhri, F. C. MacKintosh, C. F. Schmidt, C. P. Broedersz, Broken detailed balance of filament dynamics in active networks. Phys. Rev. Lett. 116, 248301 (2016).
127 A. Frishman, P. Ronceray, Learning force fields from stochastic trajectories. Phys. Rev. X 10, 021009 (2020).
128 E. Roldan, J. Barral, P. Martin, J. M. R. Parrondo, F. Jülicher, Arrow of time in active fluctuations. arXiv [Preprint] (2018). https://arxiv.org/abs/1803.04743v4 (Accessed 2 August 2020).
129 L. Zhao, J. Wang, Uncovering the mechanisms of Caenorhabditis elegans ageing from global quantification of the underlying landscape. J. R. Soc. Interface 13, 20160421 (2016).
130 M. G. Vander Heiden, L. C. Cantley, C. B. Thompson, Understanding the Warburg effect: The metabolic requirements of cell proliferation. Science 324, 1029–1033 (2009).
131 M. T. Lin, M. F. Beal, Mitochondrial dysfunction and oxidative stress in neurodegenerative diseases. Nature 443, 787–795 (2006).
132 J. Van Blerkom, Mitochondrial function in the human oocyte and embryo and their role in developmental competence. Mitochondrion 11, 797–813 (2011).
133 C. Li, J. Wang, Landscape and flux reveal a new global view and physical quantification of mammalian cell cycle. Proc. Natl. Acad. Sci. U.S.A. 111, 14130–14135 (2014).
134 W. Li, J. Wang, Uncovering the underlying mechanisms of cancer metabolism through the landscapes and probability flux quantifications. iScience 23, 101002 (2020).
135 L. Xu, J. Wang, Curl flux as a dynamical origin of the bifurcations/phase transitions of nonequilibrium systems: Cell fate decision making. J. Phys. Chem. B 124, 2549–2559 (2020).
136 K. Zhang, J. Wang, Exploring the underlying mechanisms of the Xenopus laevis embryonic cell cycle. J. Phys. Chem. B 122, 5487–5499 (2018).
137 A. San Martn et al., A genetically encoded FRET lactate sensor and its use to detect the Warburg effect in single cancer cells. PLoS One 8, e57712 (2013).
138 V. Deshpande, A. DeSimone, R. McMeeking, P. Recho, Chemo-mechanical model of a cell as a stochastic active gel. J. Mech. Phys. Solids 151, 104381 (2021).
139 T. Markovich, E. Fodor, E. Tjhung, M. E. Cates, Thermodynamics of active field theories: Energetic cost of coupling to reservoirs. arXiv [Preprint] (2020). https:// arxiv.org/abs/2008.06735 (Accessed 12 October 2020).
140 R. Pandey, S. Heeger, C. F. Lehner, Rapid effects of acute anoxia on spindle kinetochore interactions activate the mitotic spindle checkpoint. J. Cell Sci. 120, 2807–2818 (2007).
141 D. A. Beard, A biophysical model of the mitochondrial respiratory system and oxidative phosphorylation. PLoS Comput. Biol. 1, e36 (2005).
142 B. Korzeniewski, J. A. Zoladz, A model of oxidative phosphorylation in mammalian skeletal muscle. Biophys. Chem. 92, 17–34 (2001).
143 I. Tavassoly, J. Goldfarb, R. Iyengar, Systems biology primer: The basic methods and approaches. Essays Biochem. 62, 487–500 (2018).
144 M. Doi, Soft Matter Physics (Oxford University Press, 2013).
145 J. N. Israelachvili, Intermolecular and Surface Forces (Elsevier, 2015).
146 A. Baskaran, M. C. Marchetti, Hydrodynamics of self-propelled hard rods. Phys. Rev. E 77, 011920 (2008).
147 A. Peshkov, E. Bertin, F. Ginelli, H. Chat ´e, Boltzmann-Ginzburg-Landau approach for continuous descriptions of generic Vicsek-like models. Eur. Phys. J. Spec. Top. 223, 1315–1344 (2014).
148 X. Yang, M. C. Marchetti, Hydrodynamics of turning flocks. Phys. Rev. Lett. 115, 258101–258105 (2015).
149 S. Fürthauer, D. J. Needleman, M. J. Shelley, A design framework for actively crosslinked filament networks. New J. Phys. 23, 013012 (2021).
150 B. Kooijman, S. A. L. M. Kooijman, Dynamic Energy Budget Theory for Metabolic Organisation (Cambridge University Press, 2010).
151 R. P. Hafner, G. C. Brown, M. D. Brand, Analysis of the control of respiration rate, phosphorylation rate, proton leak rate and protonmotive force in isolated
mitochondria using the ‘top-down’ approach of metabolic control theory. Eur. J. Biochem. 188, 313–319 (1990).
152 K. Kornick, B. Bogner, L. Sutter, M. Das, Population dynamics of mitochondria in cells: A minimal mathematical model. Front. Phys. 7, 146 (2019).
153 T. Taillefumier, A. Posfai, Y. Meir, N. S. Wingreen, Microbial consortia at steady supply. eLife 6, e22644 (2017).
154 A. Wachtel, R. Rao, M. Esposito, Thermodynamically consistent coarse graining of biocatalysts beyond Michaelis–Menten. New J. Phys. 20, 042002 (2018).
155 J. C. Aledo, A. E. del Valle, Glycolysis in wonderland: The importance of energy dissipation in metabolic pathways. J. Chem. Educ. 79, 1336–1339 (2002).
156 H. V. Westerhoff, K. J. Hellingwerf, K. Van Dam, Thermodynamic efficiency of microbial growth is low but optimal for maximal growth rate. Proc. Natl. Acad. Sci. U.S.A. 80, 305–309 (1983).
157 J. B. Russell, G. M. Cook, Energetics of bacterial growth: Balance of anabolic and catabolic reactions. Microbiol. Rev. 59, 48–62 (1995).
158 A. Maitra, K. A. Dill, Bacterial growth laws reflect the evolutionary importance of energy efficiency. Proc. Natl. Acad. Sci. U.S.A. 112, 406–411 (2015).
集智斑图顶刊论文速递栏目上线以来,持续收录来自Nature、Science等顶刊的最新论文,追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能,每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅:

点击“阅读原文”,追踪复杂科学顶刊论文