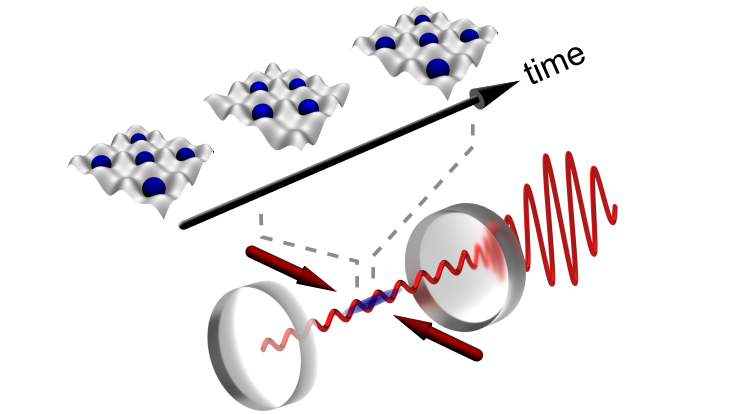
在晶体中跨越整数个晶格距离,会看到相同的晶格结构。时间晶体是传统空间晶体的类似物,其性质随着时间周期性变化,经过整数个周期会看到相同性质再次出现。传统晶体打破了空间平移对称性,时间晶体则打破了时间平移对称性。在物理学中,时间平移对称性与能量守恒相对应,所以对时间晶体的研究具有重要意义。此外,时间晶体也为理解时间和空间的区别与统一提供了新视角。
在之前的实验中,由于耗散和退相干,与环境的耦合限制了时间晶体的寿命。7月19日,PRL 发表的一项最新研究,第一次利用耗散实现了稳定的时间晶体,在受驱动的开放原子-腔系统中观察到不同棋盘密度波图案的周期性转换。APS 发表文章“Time Crystals in Open Systems”对这项工作进行了评论,以下是文章的翻译。
研究领域:时间晶体,耗散与退相干,对称性破缺,时间和空间
Zongping Gong, Masahito Ueda | 作者
黄泽豪 | 译者
梁金 | 审校
邓一雪 | 编辑
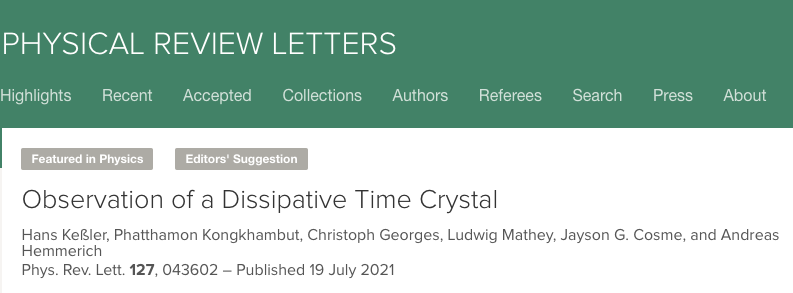
论文题目:
Observation of a Dissipative Time Crystal
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.127.043602
由Frank Wilczek(理论物理学家、2004年诺贝尔物理学奖得主)在2012年提出的时间晶体是传统空间晶体的时间类似物 [1]。传统晶体需要打破空间平移对称性,时间晶体则需要打破时间平移对称性。
这种奇异的动力学物相已经在各种实验平台上被实现,但在所有情形下,时间晶体相都处于受相干调控的封闭系统中[2]。7月19日,来自德国汉堡大学的汉斯·凯勒(Hans Keßler)和同事们在 PRL 上发表论文宣布,首次在开放量子系统中观察到时间晶体行为[3]。
时间晶体在与时间无关(即能量守恒)的系统中实现时,可以打破连续时间平移对称性,在周期性驱动(Floquet)系统中实现时,可以打破离散时间平移对称性。前者是Wilczek最初设想的情形,已被被证明不可能在短程关联系统的基态或热平衡态中实现[4]。但是周期性驱动的系统,其组分采用的空间构型以驱动周期的倍数(通常是两倍)为周期循环出现,已经在一些有强无序和关联的封闭自旋系统中得到证实[5]。
为了将“离散时间晶体”与拉比振荡*等其他动力学现象区分开来,这种周期倍增必须表现出“刚性”;也就是说,它必须对系统参数或驱动规则中的小扰动具有鲁棒性。为了创造具备必要刚性的离散时间晶体,一种广泛使用的方法是,驱动一个对称破缺的系统,在每个驱动周期内从一个对称破缺态切换到另一个对称破缺态。
译注:拉比振荡(Rabi oscillations)是一个二能级系统在振荡的驱动场作用下表现出的周期性行为。一个二能级系统包含一个低能量的基态和一个更高能量的激发态,例如当一个二能级原子系统被一束相干光照射时,它会周期性地吸收光子并(通过受激辐射)重新辐射光子,发生拉比振荡。
图1. 时间晶体在两种状态之间来回切换,它们是在时间而非空间上重复的晶体。周期性驱动的时间晶体以驱动周期的整数倍为周期循环出现,比如驱动力作用两次,时间晶体只振荡一次,这与钟摆响应周期性的驱动力不同。| 来源:Maylee for Quanta Magazine
到目前为止,所有关于离散时间晶体的实验证明都使用了封闭系统,这就留下了一个问题:能否在存在耗散和退相干的情况下实现它们?
这个基本问题具有实际意义,因为真实的系统永远无法与周围环境完全隔离。虽然耗散通常会破坏时间晶体的序,但在某些情况下,如果系统-环境耦合可以被适当地调控,这个序就会保留下来。在量子计算和量子态工程(quantum-state engineering)中,这种调控已经允许耗散作为一种有用的资源加以利用[6]。实验原子、分子和光物理的最新进展,使得用这种方法在开放量子系统中实现新奇的动力学序成为可能[7]。
Keßler和同事们带来的进展提供了强有力的证据,表明离散时间晶体可以存在于受驱动、开放的原子腔系统中。他们的实验延续了此前关于受驱动的开放Dicke模型中的时间晶体序的理论预测[8]。开放的Dicke模型描述了一个由泵浦激光驱动,并与单个有损光子模式耦合的二能级原子系综。该系统表现出耗散的超辐射(superradiant)相变,这意味着如果超过一定的泵浦阈值,原子系综将变得空间有序,同时原子将相干地发射光子。
图2. Dicke模型描述了由二能级原子系统和光场的相互作用。| 来源:AG Hemmerich
在首次实验演示中[9],Keßler和同事们使用腔中的玻色-爱因斯坦凝聚态(BEC),系统的两个能级表现为原子的运动自由度。尽管第一次演示是静态的,他们还是通过改变泵浦激光的强度,来诱导原子和腔中光子的耦合以驱动系统。
研究团队使用两种方法测量了系统的动力学。首先,他们通过检测从腔内泄漏的光子,来持续监测腔内光子的相和数量。其次,他们通过释放BEC并观察其扩散(即飞行时间图像,time-of-flight image),来测量原子在给定时刻的动量分布。
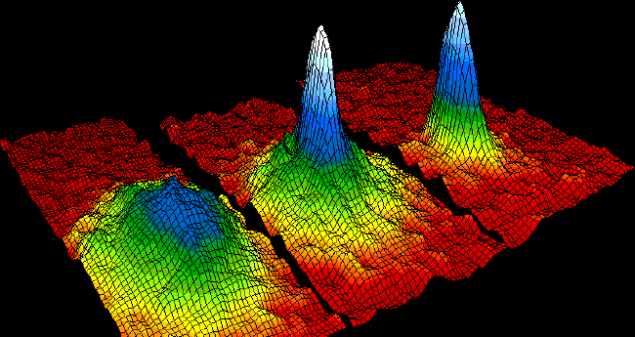
图3. 玻色-爱因斯坦凝聚是指,当温度接近绝对零度时,大量粒子(一般是玻色子)自发占据系统基态的现象,此时粒子所处的状态被称为玻色-爱因斯坦凝聚态。在该实验中,BEC被束缚在光势阱中,当势阱关闭,不再受到约束的原子将从势阱中扩散开来,通过测量原子到达探测器的飞行时间分布可计算出原子团的温度、动量分布等物理量。| 来源:NIST/JILA/CU-Boulder
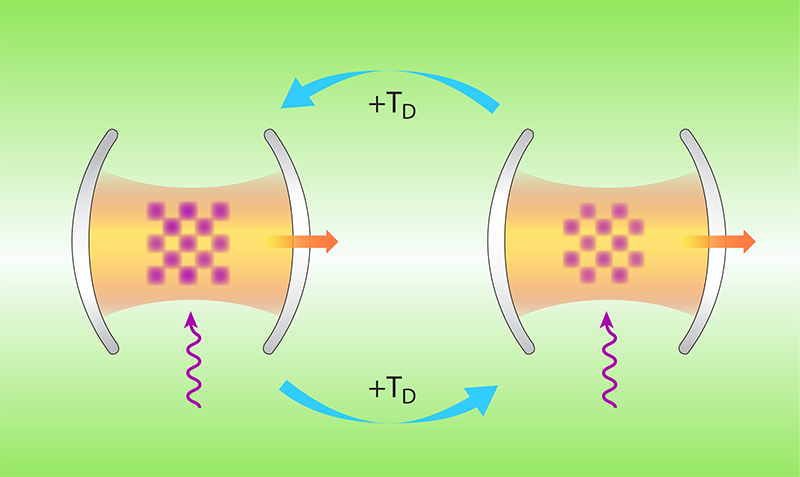
这些测量结果表明,对于恰当选择的参数,系统会周期性地在两个对称性破缺的超辐射态间转换,BEC在两种状态下呈现出不同的棋盘图案(checkerboard pattern)。状态之间切换的完整周期是驱动周期的两倍,并且在该驱动期间对非周期性的时间无序具有鲁棒性。虽然这种鲁棒性不同于通常在离散时间晶体中——其中扰动系统是严格周期性的——看到的刚性[5],但它类似于空间晶体的鲁棒性,可以容许空间不均匀的杂质。
图4. 新实验中演示的耗散离散时间晶体的示意图。在每个驱动周期 TD 中,腔中被驱动的玻色-爱因斯坦凝聚态在两种对称破缺的密度波态(棋盘图案)间切换一次。紫色箭头表示泵浦激光,橙色箭头表示光子从腔中泄漏。| 来源:Z. Gong and M. Ueda; adapted by APS/Carin Cain
该团队观察到的周期倍增行为让人想起非线性光学中的一种现象,即次谐波发生器(subharmonic generator)产生的输出光子频率是输入光子的整数分之一(通常是1/2)。然而,两者在概念上存在差异:离散时间晶体的振荡是系统本身的动力学特性,而次谐波的产生与输出信号直接相关,与系统无关(这里的“系统”是转换输入光子的介质)。此外,次谐波的产生并不需要时间晶体的决定性条件——在扰动下具有鲁棒性。不过,创造离散时间晶体获得的深刻洞察是否有助于实现高效的次谐波生成?思考这个问题可能很有趣。
Keßler和同事们证实的一个时间晶体的局限性是,这种振荡会在几个周期后衰减。衰减主要来源于BEC的原子损耗,这实际上减少了系统中集体原子-光子的耦合,并将其推出超辐射相。为了延长这种时间晶体的寿命,未来的一项重要任务是克服原子损耗。
调整腔内光子损耗和原子间相互作用(其影响被本实验中的原子损耗所掩盖)也将是很有趣的。这种调整可能会揭示标准半经典(平均场)描述[10]没有预测的新现象,并证实时间晶体序确实是通过耗散而稳定下来[8]。
除了Keßler和同事们使用的周期性驱动系统,研究人员尚未在与时间无关的开放系统中展示连续时间晶体[11]。虽然这种时间晶体已经被证明不可能在平衡系统中实现[4],但应该可以在远离热平衡的系统中实现。
从更广泛的角度看,该实验提供了一个原型示例,展示了在持续监测下如何研究量子多体系统中驱动、相互作用和耗散之间丰富的相互作用。对于非平衡开放量子系统中很大程度上未被探索的相结构和动力学现象,我们期望这项工作将催生更多相关理论和实验研究。
原文:
https://physics.aps.org/articles/v14/104
[1]F. Wilczek, “Quantum time crystals,” Phys. Rev. Lett. 109, 160401 (2012).
[2]J. Zhang et al., “Observation of a discrete time crystal,” Nature 543, 217 (2017); S. Choi et al., “Observation of discrete time-crystalline order in a disordered dipolar many-body system,” 543, 221 (2017).
[3]Hans Keßler et al., “Observation of a dissipative time crystal,” Phys. Rev. Lett. 127, 043602 (2021).
[4]H. Watanabe and M. Oshikawa, “Absence of quantum time crystals,” Phys. Rev. Lett. 114, 251603 (2015).
[5]N. Y. Yao et al., “Discrete time crystals: rigidity, criticality, and realizations,” Phys. Rev. Lett. 118, 030401 (2017).
[6]F. Verstraete et al., “Quantum computation and quantum-state engineering driven by dissipation,” Nat. Phys. 5, 633 (2009).
[7]H. P. Lüschen et al., “Signatures of many-body localization in a controlled open quantum system,” Phys. Rev. X 7, 011034 (2017).
[8]Z. Gong et al., “Discrete time-crystalline order in cavity and circuit QED Systems,” Phys. Rev. Lett. 120, 040404 (2018).
[9]K. Baumann et al., “Dicke quantum phase transition with a superfluid gas in an optical cavity,” Nature 464, 1301 (2010).
[10]B. Zhu et al., “Dicke time crystals in driven-dissipative quantum many-body systems,” New J. Phys. 21, 073028 (2019).
[11]F. Iemini et al., “Boundary time crystals,” Phys. Rev. Lett. 121, 035301 (2018).
集智斑图顶刊论文速递栏目上线以来,持续收录来自Nature、Science等顶刊的最新论文,追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能,每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅:

点击“阅读原文”,追踪复杂科学顶刊论文