意识机器?——AI视野(六)

近年来一些心理实验表明人类的自由意志可能是幻觉,而LSTM之父Jürgen Schmidhuber可能早已经设计出了意识机器。
好久没有续写这个”AI视野”系列了。今天有机会,就让我们来聊一聊机器是否能够具备自我意识——这一重磅、高能、危险的话题。人们普遍认为,意识(Consiousness),特别是自由意志(Free will)构成了人之所以为人,从而区别于机器的最后一道防线。而本文想表达的观点是,其实这一道防线早就不存在了。首先,近年来有关意识的一系列心理学实验表明所谓的自我其实有两个,一个称为陈述型(Narrating)自我,一个称为体验(Experiencing)自我;所谓的自由意志不过是陈述型自我给自己编的一个故事而已。其次,通过目前的计算技术我们完全可以构造出一个自我模拟的自指机器(Self-referential Machine),它也具备两套体系,一个负责执行算法,另一个则专门负责对自我进行模拟(描述),这种机器会表现得就“像”一个具有自我意识的系统,以至于我们可以用这样的系统来定义所谓的“自我意识”。
早在2003年LSTM之父Jürgen Schmidhuber就具体设计出来了一种称为“哥德尔机”(Gödel Machine)的装置,它具备一个求解器和一个搜索器,这个搜索器就是前文所说的模拟装置,也就是人类意识中的“陈述自我”;而求解器就是前文的执行装置也就是人类意识中的“体验自我”。Schmidhuber指出这种机器一旦设计出来了,就可以通过不断搜索更好地优化效用的方式来完成模拟优化,再通过自我修改代码的装置不断改进自身,从而表现出全局最优的运作模式。人们普遍认为哥德尔机是目前最强大的通用人工智能设计,并有可能引发智能爆炸。
自由意志幻觉——来自实验的启发
首先,我们对近几十年来人们对意识问题的三个极其重要的实验进行回顾。第一个实验告诉我们其实我们每个人的头脑中都住着两个自我,一个负责决策,另一个负责解读;第二个实验进一步揭示出这个陈述自我的性质,它会在一定条件下编纂故事;第三个实验则告诉我们很可能我们认为的自由选择也是陈述自我编的一个故事而已。
裂脑人试验
人类的左脑和右脑是靠一种被称为胼胝体的东西相连在一起的。但是有一种病人称为“裂脑人”,他们脑袋中的那个连接装置胼胝体被切开了,但他们还可以正常的生活。于是,在二十世纪六十年代,这些裂脑人成为了神经科学家们,特别是斯佩里(Roger W. Sperry)等人的实验对象。科学家们通过巧妙地设计试验,让我们得以看到裂脑人甚至是我们自己不为人所知的一面。
在如下图所示的实验中,我们用一个中间的挡板把裂脑人左右两眼的视野完全隔离开,这样他的左眼只能看到左边的画,右眼只能看到右边的。当我们呈现左边为雪景右边为鸡爪的画面给被试的时候,这两种景象就分别映射到了右脑和左脑中(由于左脑连接的是右侧身体,右脑连接的则是左侧身体)。接下来,实验人员要求被试在卡片上选择与看到的画面相关的东西(两只眼睛都能看到所有的卡片)。这个时候,裂脑人的左手(被右脑控制)选择了铲雪的铁锨;右手(被左脑控制)则选择了公鸡。
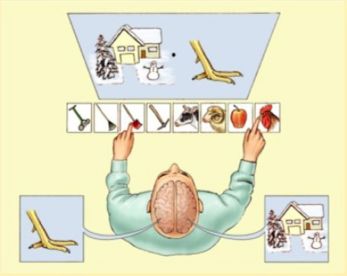
这说明,裂脑人的两个彼此隔离的大脑作出了两种完全不同的决策,体现得像是两个不同的人。更有意思的是,当挡板撤离后,左右脑都能看到对方的选择了。这个时候实验人员问被试,“你为什么左手选择铁锨呢?”我们知道,左脑是负责语言的半球,而右脑主要负责视觉感知,却没有表达能力。所以,虽然右脑选择的是铁锨,而它并不会解读。左脑选择的是公鸡,但却与右脑的选择相冲突。那该怎么办呢?于是,左脑神奇地编了一个故事:“我选择铁锨是因为我要清理鸡棚!”
斯佩里通过大量的类似的裂脑人实验向我们展示了这样一个结论,我们的左右脑不仅表现得像两个独立的意识体,而且由于左脑具备一种编造故事的能力,它往往能够把右脑的行为进行重新解读。
冰水挑战
前面的实验对裂脑人的左右脑进行了物理分割。而诺贝尔经济学奖得主,著名心理学家丹尼尔.卡尼曼(Daniel Kahneman)则相信,我们身体里本身就住着两个自我,卡尼曼把她们叫做:“陈述自我”(Narrating self)和“体验自我”(Experiencing Self)。前者专职负责讲故事,甚至在很多时候都是讲给我们自己听的;另一个则主要负责体验、执行。这两个自我经常配合在一起行动。有意思的是,我们的记忆主要是听从这个叙述自我的,而这个家伙会经常扭曲事实、编纂故事。下面,就让我们来看看卡尼曼做过的实验:冰水挑战。
卡尼曼让被试将手放到很冷的冰水中一段时间(见下图)。实验分两次进行,第一次进行60秒,第二次进行90秒。但在第二次试验进行到60秒的时候,实验人员会偷偷注入了一些温水,让被试疼痛的感觉减轻一些,但是被试并不知情。
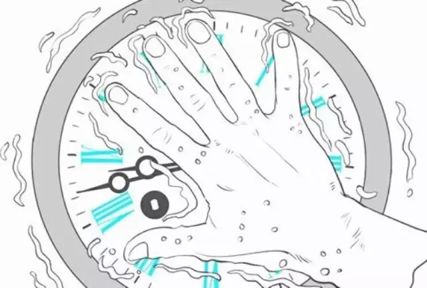
在分别做完两次试验之后,实验人员会问被试,如果必须重复实验,你更希望重复哪一次的实验。出乎意料的是,有80%的被试都选择第二种,即长达90秒的实验。
卡尼曼给出的解释是,我们的陈述自我有一种特性,它只对整个试验过程中疼痛的最高值和最后一个时刻的疼痛值敏感,这就是所谓的“峰值-尾值定律”(peak-end rule),并且会忽略体验所持续的时间。所以,在第二个实验中,由于最后30秒的体验没有那么的痛苦,所以被试最终的选择听从了陈述自我的感受,认为第二个实验更好受一些,尽管它让被试受苦的时间更长也没关系。
这个实验似乎还能够解释其它一些“痛并快乐”的现象。就比如女人生小孩据说是疼痛级别最高的一种经历,但是当女人回忆生产那个瞬间的时候却总是伴随着温馨和幸福。原因就在于在生完小孩的那个时刻所体会的幸福远超过了过程中的痛苦。于是,陈述性自我选择了过滤掉那些痛苦体验,而记住了小生命出生的幸福。
自由意志幻觉?
前面的两个实验告诉我们,我们不仅每个人都是人格分裂者,而且大多我们意识到的体验都不过是陈述性自我编撰的故事。那么,在接下来要介绍的实验中,我们更能深切的体会到,所谓的自主选择、自由意志也不过是一种假象,很可能就是“陈述自我”用来哄骗自己而编纂的一个故事。
这个实验是由Benjamin Libet于2008年领导做出的,其结果发表在了Science杂志上,曾引起了科学界和哲学界的轰动。在实验中,他让被试手持一个按钮,自主选择任何一个时间按下这个按钮,然后被试会通过盯住面前钟表上的秒针相应位置来报告做出决策的时间。于此同时,Libet通过脑电装置来监测被试大脑活动的模式(预备电位),并根据这些模式来预测被试何时按下按钮。整个实验装置如下图所示。
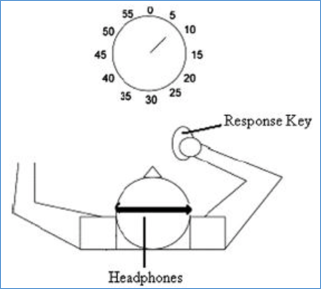
实验的结果表明,科学家可以通过读取大脑活动模式来提前预测被试是否按电钮的决策,而且可以比被试报告的时间提前几秒钟。
如果按照前面的实验推论,我们的心智分成了负责体验、决策的自我和负责陈述的自我两部分。那么这个做出按电钮动作的自我就是体验自我做出的,而负责报告按电钮时间的自我就是陈述自我。科学家通过大脑电信号活动模式所做出的提前几秒钟的预测表明,我们实际上在自认为有意识地做出按电钮这个动作之前就已经由体验自我和身体把决策做出了。我们的意识,或陈述自我并没有起到任何主导性作用,它只是被动地将这个按钮动作进行了重新解释,从而报告出了时间。
这个实验最大的争议点就在于,它从某种程度上否定了“自由意志”(Free will)的存在性。也就是说,我们并不像我们通常认为的那样可以由自我意识来决定、控制做出按电钮的动作。
在这里我们需要澄清一下“意识”、“自我意识”以及“自由意志”之间的区别和联系。首先,“意识”(Consiousness)是指一种觉知(awareness)的能力,它是指我们的心智能够对外界事物以及心理过程进行感觉的能力。“自我意识”则是说这种意识能力不仅能够觉知外在事物,还能够觉知这个觉知能力,即意识本身。所以我个人认为自我觉知(Self-awareness)能更好地表达意识的这种能力。后面我们会看到,这种能力就是计算理论、数学之中的自指(Self-reference)。“自由意志”则是强调意识对客观事物的反作用特性,也就是意识可以凭借自己的意愿来决定做什么。
Libet的实验告诉我们,我们可能并没有自由意志,至少我们的意识并不参与决策过程。因为,真正的决策早在我们意识到之前几秒的时间就已经被体验自我做出了。
实验总结
把这三个实验连在一起,我们能得到如下几个结论:
-
我们每个人体内都存在着两个自我,一个负责体验和执行,一个负责表述;
-
那个陈述性的自我会通过虚构故事来“欺骗”我们自己;
-
我们习以为常的自由意志很可能就是这个陈述自我编造的一个故事。
这最后一个结论的确具有一定的颠覆性,它直接指出了所谓的自由意志不过是一种假象。我们充其量仅仅具备自我意识而已,也就是我们可以觉知到自己的存在,也能觉知到我们所做的一切,但是这种觉知并不能反过来作用到我们的行动上来。
用图形表述上面这一点转变会更清楚:
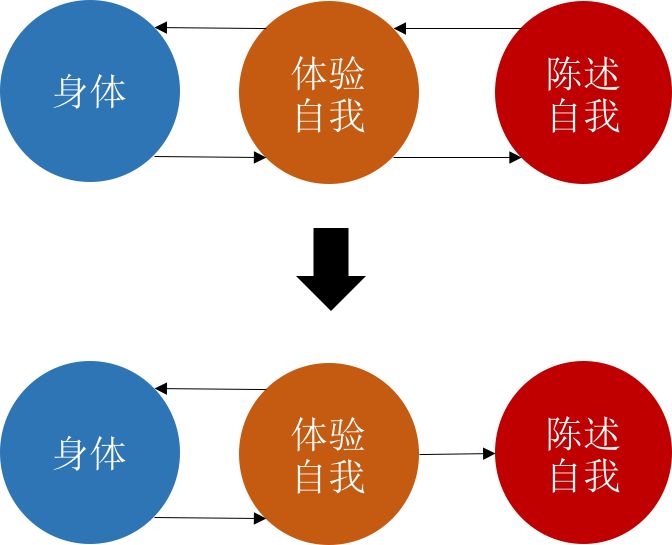
我们的认识从上图的模式转变为了下图的模式。尽管我们对这一转变很不情愿,但却不得不接受。因为,越来越多的科学研究结果表明,其实我们人就是一个算法机器,迄今为止,我们并没有找到任何一个反面的证据说人的过程不能被算法模拟。既然自由意志是幻觉,人不过是个算法机器,那么,机器和算法本身为什么不能具备意识,甚至是表面上看起来的“自由意志”呢?
意识机器
在结束了心理学之旅后,就让我们来进入机器的世界。请注意,在这里我并没有声称任何一台机器,甚至是任何足够聪明的超级智能体具有意识。我想说的是,机器必须要具备一定的条件才能具备意识,而目前这样的机器尚没出现,但这并不意味着我们原则上无法创造出它来。更重要的是,意识所需要的条件和智能完全就是两码事。
既然我们已经破除了“自由意志”的迷信,并且认识到所谓的自我不过就是一个双系统,一套系统负责相对“机械”地解读信息、作出决策;另一套系统则对这些决策进行解释、表述。
那么,按照这套标准,我们就会发现,只要一台机器具备了自我模拟(Self-emulating)的能力,它就具备了“意识”。什么是这种自我模拟的能力呢?这就是指一台机器能够在内部开一个虚拟机,并用这个虚拟机来模拟自己在任何一个时刻的运行。于是,这个模拟机就构成了前文所讲的“叙述自我”,而其它的软件部分就构成了前文所讲的“体验自我”或“执行自我”。由于这台机器可以在虚拟机中投射它自身以及所有的动作,所以它就具备了“自我觉知”的能力。从外界表象上来看,它可以表现得具有自我意识。
这样的机器能造出来吗?答案是肯定的,计算理论早在二十世纪初就为这类机器的实现铺平了道路。接下来,就让我们看看,我们该如何一步步地造出这样的自我模拟机器。
内嵌虚拟世界
机器要想具备自我模拟的能力,那么它首先要实现一个内嵌的虚拟世界。什么是内嵌的虚拟世界?其实就是所谓的虚拟机——即奔跑在当前计算机中的一套虚拟系统。这套系统有它自己的虚拟硬件,以及虚拟软件。用过Docker、VMWare的人都很清楚,这种内嵌的虚拟系统不仅早就可以被造出来,而且具有可以隔离病毒等优良的特性。
我们可以将内嵌的虚拟世界理解成一面镜子。它可以映射真实世界里的东西,但它本身却比现实低了一个层级,所以它看起来更“假”。我们也可以从数据和程序的角度来理解:虚拟系统相对于真实机器来说就是数据。数据总是被动地由更加“真实”的机器所操纵。
我们要感谢图灵的伟大发现,通用图灵机(Universal Turing Machine)的存在保证了我们可以通过现有的计算机来实现这种内嵌的虚拟世界,而且这种内嵌的虚拟层可以无限地延伸下去。也就是,我们可以在虚拟机上再安装虚拟机,以及虚拟机上的虚拟机……。
模拟自我
好,当一台机器具备了内嵌虚拟层还不够,它还需要完成模拟自我的过程。也就是说,我们要让这台虚拟机器模拟它自己的运行动作。这在镜子的比喻中也就是我们要让镜子自己照自己。你很快就发现,这是不可能的。至少在镜子这个例子中,如果我们不借助外界(例如另一面镜子),这个镜子自身无法完成照射自己。
同样,在机器世界中,要让一台安装了模拟器的程序模拟自己,表面上看是不能完成的。不难想象,由于机器的内嵌虚拟层本身就是这台机器的一部分,于是,要想让虚拟层模拟机器自己的动作,就必须包括它的虚拟层,于是我们必须要有一个虚拟层的虚拟层。这样一来,我们就需要有无穷多的虚拟层,而且每一个虚拟层都要做同样的事情,模拟它上一层次的动作。你会发现,我们的机器很快便触及到了无穷多的虚拟层次,以至于怎么可能在有限的时间和空间内完成它呢?
幸运的是,在计算理论、数理逻辑以及递归函数论(人们早已证明,这三种系统完全等价)中,人们早已经发现了一种巧妙地逃离这种无穷的方式。在数学中,这叫做不动点(fixed point);在递归函数论中,这叫做Kleene第二递归定理;在计算机程序中,这叫做“蒯恩”程序。事实上,康托尔运用这种技巧证明了实数比自然数多;罗素用这种技巧构造了罗素悖论;哥德尔用这种技巧完成了哥德尔定理的证明;图灵用这种技巧构造了图灵停机问题,指出了机器运算的极限;冯诺依曼用这种技巧制造了自复制的程序。现在,我们同样可以用这种技巧构造可以模拟自身的程序。有关这种技巧的详细说明请参考附录。
在这里我想说明的是,这种被称为“蒯恩”(以美国著名哲学家蒯恩Quine为命名)的技巧,本质上讲可以实现这样的效果:执行一段包括蒯恩的模拟器就和将这个程序自己的源代码拿出来在模拟器上跑效果完全一致,所以它看起来就像在模拟自己(实际上我们没有任何手段能从运算结果上区分二者)。于是,我们便巧妙地绕过了无穷层次。
解读意识
其实,这种能够模拟自身运作的机器就可以被称为是具有自我觉知能力了。我们只需要将自模拟程序中的正在模拟自身的虚拟机理解成前文所说的陈述自我,而将整个机器的其它部件都看作是体验自我和身体,那么这种自模拟程序就跟前文说到的人类的自我系统没有什么两样。具体的,我们有这样的对应关系:
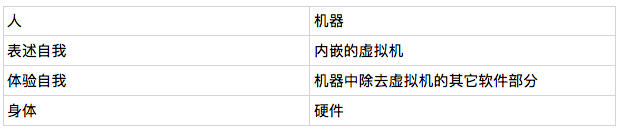
为什么可以这样理解呢?这里面有几层含义。
首先,所谓的虚拟其实就是描述。前文我们已经将虚拟机比喻为镜子,意思就是说这个虚拟层要能够形成对外在世界的描述。
其次,这是一台自我模拟的机器。根据递归定理,这台机器的所有部分,包括内嵌的虚拟机中的动作,都可以在虚拟机中找到对应。也就是说这个陈述自我知道什么是“我”,我在做什么,以及知道这个觉知(或模拟)过程本身。
最后,如果我们将内嵌虚拟机接上一个输出接口,允许它用自然语言吐出字符串,那么这个虚拟机就更像表述自我了,它可以向外界输出表述。
既然从功能上说,我们的自模拟机器与陈述自我+体验自我一致。下面,就让我们来看看,为什么说这种自模拟机器表现的就像具有自我意识一样。
首先,这台机器是具备觉知能力的。这里,所谓的觉知其实就是在虚拟层来反映真实世界,当然也包括这台机器本身的所有部分,显然这台机器是可以做到的。
其次,这台机器是具备自我觉知能力的。根据蒯恩技巧,只要机器开始运行,它的表现就像是在虚拟层模拟它自身一样。如果我们将模拟器称为觉知能力的主体,那么它模拟自身就自然可以称为自我觉知了。
更有意思的是,当外部观察者观察这台机器运行的时候,TA会产生这台机器具备“自由意志”的幻觉。这是为什么呢?其实道理还是在于蒯恩。
对于任何一个配备了蒯恩的程序来说,它有这样的效果,它整体完成的动作和虚拟机上完成的动作看起来是一模一样的。于是,我们便无法分别究竟是这台机器“被动”地根据真实层的“物理法则”来做出动作还是根据虚拟层“意识”来作出的动作。于是,对于观察者来说,一个虚拟的因果箭头就可能被生生造了出来:这台机器在根据它自己的意识(称述自我)而行动。那么,我们也自然可以称这样的机器具备自我意识,甚至自由意志了。
其实这个道理就像你照镜子,假如一个从来不知道镜子为何物的外星人观察你们,他有可能会得出来你在按照镜子里面的像而运动,它是因,你是果。所以,当你和你的虚拟重合为一,你就能给外部观察者生硬地创造出一个因果箭头。自我模拟机器正是这样工作的。
哥德尔机——史上第一台意识机器

个人八卦
从我个人的经历而言,最早意识到“自我模拟”程序非常重要是在2007年左右。那个时候我正在参加Stephen Wolfram办的A New Kind of Science(简称NKS)的暑期学校。一个叫做Mathew的MIT的年轻老师给我们讲图灵停机理论。他当时概括说,正是因为我们可以构造出这样一个可以通过自己源代码来“模拟”它是否停机的程序,而这个程序让外界的观察者看到的表现,和它自己“声称”的表现并不一致,所以才证明了图灵停机问题的不可判定性。当时,我立刻意识到:自我模拟是问题的关键。(恰恰就在Wolfram的这本NKS中,他还讨论了自我模拟的元胞自动机)。
后来看关于计算理论的书:Nigel Cutland的Computability: an introduction to recursive function theory,我才了解到Kleene第二递归定理与自我模拟程序的关系。甚至在这本书中,Nigel Cutland根据第二递归定理专门讨论了这种自我模拟程序的可能性。在该书中,他称该程序为“自我反省”(Self-retrospectation)的程序。当时我就想为什么没有人动手把这种自反省程序做出来呢?
结果,最近我了解到,早就有人动手研究这种自模拟程序了,这个人就是大名鼎鼎的Jürgen Schmidhuber。也许你对这个名字还不熟悉,但你一定知道LSTM(长短时记忆网络),这个LSTM可是Google机器翻译、对话系统背后最大的功臣。LSTM的发明者正是Schimchumber这位德国老先生。令人意想不到的是,他早在2006年的时候就提出了哥德尔机(Godel Machine),它可以被称为人类历史上第一台具备自我模拟、自我反省,甚至自我意识的人工智能机器,尽管它现在还远没有被造出来。
哥德尔机的构成与工作原理
从整体结构上来讲,哥德尔机实际上与我们之前讲的自我模拟程序非常类似,它由两部分构成:1、通用搜索器,这对应了自我模拟程序中的虚拟机;2、问题求解器,它对应了自我模拟程序的其它部分。但是,在哥德尔机中,求解器是一个几近完整的强化学习系统,它还包括了输入输出装置,从而它就像一个机器人一样能够实时地感知外界环境,并能对环境进行响应。与此同时,哥德尔机还有一个效用函数,它的目的就是为了不断地提升这个效用函数,这些都是自我模拟程序尚缺乏的部分。这些多出来的装置就可以让哥德尔机不仅能够实现自指,同时还能够以最优的方式求解问题。
具体来讲,哥德尔机是这样工作的。首先,哥德尔机内部存在一套编码系统,它可以将哥德尔机的硬件、软件甚至是当前的状态、效用函数,以及通用搜索器等等全部编码成数学命题。这种做法实际上就是哥德尔在1932年证明哥德尔定理的时候所使用的方法。有了这样的编码系统,哥德尔机就可以将机器工作的所有状态当作数学定理来讨论。
其次,通用搜索器可以不断地搜索一条数学命题的证明,从而判断它的真伪。这样, 哥德尔机就有可能完成牵扯到它自身问题的求解了。例如,假设关于哥德尔机的一个命题是:“如果我持续地原地转圈,那么天上就会掉下一个馅饼来,从而提高我的效用。”那么,这个语句判断就有可能被编码成搜索器可以搜索的命题。于是,搜索器开始展开搜索,它会利用形式逻辑的推理法则展开运算,看看该条命题是否可以被推导出来。假设搜索器最后证明了这条命题是真的,那么哥德尔机就可以将策略“持续原地转圈”装载到哥德尔机的执行装置中。于是,哥德尔机就会不停地原地转圈了。
所以,通过这样的方式,哥德尔机就能持续地搜索可提升自己效用的方案,并利用更好的方案改写自己的源代码,从而完成“自省”的学习过程。据证明,哥德尔机与当前的强化学习算法有异曲同工的效果,能够在一边探索的时候一边学习。不过,Schimchuber证明,哥德尔机可以避免局部最优的问题,这就比一般的强化学习算法高明很多了。之所以它有这种能力,就是因为搜索器的妙用:它只有在证明了一套方法可以提升效用的时候才真正使用它。
我们不难看出,实际上搜索器就是我们前面说的虚拟机。所谓的搜索就是一套模拟过程。而哥德尔机允许对自身状态进行编码形成数学命题就相当于机器可以模拟自身的运作。所以,我们说哥德尔机就是对自我模拟程序的一次实现。
为了让我们的比较更具体,我们列出了下表:

哥德尔机与自我意识
Schimchuber个人也认为这个哥德尔机可以看作是具有自我意识的系统,例如他在J. Schmidhuber. A Technical Justification of Consciousness. 9th annual meeting of the Association for the Scientific Study of Consciousness ASSC, Caltech, Pasadena, CA, 2005. 这篇文章中就表达了这样的观点:长久以来我们对意识问题一直争论来争论去而没有定论,但是我们连什么是意识都还说不清楚。
与其这样,不如让我们用哥德尔机来反过来定义意识。只要程序能够模拟自身、改造自身,那么我们就可以将其称为具有自我意识的。
所以,你会看到,哥德尔机的意义也许并不单纯在于它会求解问题,而是在于它与图灵机一样,可以为我们讨论自我意识的话题奠定一个程序的基础,或称一种标准。从此以后,意识问题就不再神秘了。
哥德尔机的执行
看起来这个哥德尔机非常的复杂,它能够被实现出来并执行计算吗?Schimchuber自己给出了回答。他把哥德尔机的实现总结成了两篇文章:B. R. Steunebrink, J. Schmidhuber. Towards an Actual Gödel Machine Implementation. In P. Wang, B. Goertzel, eds., Theoretical Foundations of Artificial General Intelligence. Springer, 2012. ,B. Steunebrink, J. Schmidhuber. A Family of Gödel Machine Implementations. In Proc. Fourth Conference on Artificial General Intelligence (AGI-11), Google, Mountain View, California, 2011。其中,他主要讨论了哥德尔机执行的关键要点就是机器的自指能力,并建议采用类似于Schema这样的语言来实施哥德尔机。
这里关键的问题在于复杂性。由于一个自我模拟系统需要双层系统,这就导致一层的简单性会带来另一层的复杂性。例如,如果我们选择了汇编语言,它可能具备一套很小的指令集,但是要实现一个自指的系统可能就会不简单。相反,如果你的系统设计就是针对自指的,例如lambda演算,那么它在自指部分很简单,但是机器本身的编译器却会很复杂,于是导致我们在虚拟层实现整个机器的自我模拟会比较复杂。
总之,尽管在理论层面我们知道设计出哥德尔机原则上是可行的,但是,由于双层系统的实现本身是非常困难的,因此哥德尔机尚没有真正的做出。
智能爆炸
不过,我们还是不妨脑洞一下这样的机器做出来之后会有什么结果呢?由于哥德尔机具备不断自我改善自己代码的能力,因此,有人认为一旦它被制造出来就会引发所谓的“智能爆炸”(Intelligence Exploration)。智能爆炸就是说,这个智能系统可以通过不断地提高自己的能力而提高,这个过程会越来越快地持续下去,从而很快超过人类的智能。一旦达到了这样的智能,哥德尔机自己就会设计出哥德尔机,从而让整个智能过程加速,这就导致了智能爆炸。
目前,人们普遍认为有两种途径达到技术奇点(Technology Singularity),一种途经是通过硬件性能的不断提升,类似于摩尔定律;另一种途径则是通过软件途径,即智能爆炸。由于软件设计上的革命性进展更加不可预期,也无法被人类控制,因此认为智能爆炸的途径会更有可能突破技术奇点。
结论
本文从近年来发展出来的几个心理学实验出发指出所谓的自我意识,特别是自由意志很有可能是陈述性自我编造的一种幻觉:从我发向身体的这个因果箭头并不存在;所有的因果箭头就是环境到身体再到体验自我,然后体验自我再传向身体,再传给外界。陈述性自我只不过对整个过程进行了解读,并额外“虚构”出了意识到体验自我和身体的因果箭头。
既然破除了自由选择的迷信,那么人体就和机器没有区别。换句话说,机器也完全有可能模拟看起来具有意识的人类。我们只需要制造出一个同样具有两种自我的机器:一种虚拟的机器(陈述自我)和一种纯算法的执行机构(体验自我),那么这种机器就可以表现得像个有自我意识,甚至自由选择的装置了。我们甚至可以用这样的系统反过来定义自我意识。
类似的机器已经被Jurgen Schimchumber设计了出来,它被他称为哥德尔机。哥德尔机包括两个部分,一个是通用搜索器(相当于内嵌的模拟机器);另一个是求解器(相当于执行系统)。在这样的装置下,哥德尔机可以通过在模拟器上搜索而寻求让自己不断优化的方案。我们只需要将搜索到的虚拟代码装载到实际的执行系统上,那么哥德尔机就可以不断地修改自己的代码而提升下去。人们担心,这种装置一旦制造出来,就有可能引发智能爆炸,从而导致技术奇点的来临。
附录
蒯恩技巧
这种自我模拟的实现看起来是不可能的,但是数学家们实际上早就发现了一种技巧来克服这种不可能性。美国知名哲学家蒯恩(W.Quine)发明了一种程序,从而将它形象化、实例化。所谓的蒯恩就是一段计算机代码,运行它以后,它就可以把自己的源代码原封不动地打印出来。例如,我们可以用Java语言写下一段蒯恩:
public class Quine
{
public static void main(String[] args)
{
char q = 34; // Quotation mark character
String[] l = { // Array of source code
"public class Quine",
"{",
" public static void main(String[] args)",
" {",
" char q = 34; // Quotation mark character",
" String[] l = { // Array of source code",
" ",
" };",
" for(int i = 0; i < 6; i++) // Print opening code",
" System.out.println(l[i]);",
" for(int i = 0; i < l.length; i++) // Print string array",
" System.out.println(l[6] + q + l[i] + q + ',');",
" for(int i = 7; i < l.length; i++) // Print this code",
" System.out.println(l[i]);",
" }",
"}",
};
for(int i = 0; i < 6; i++) // Print opening code
System.out.println(l[i]);
for(int i = 0; i < l.length; i++) // Print string array
System.out.println(l[6] + q + l[i] + q + ',');
for(int i = 7; i < l.length; i++) // Print this code
System.out.println(l[i]);
}
}看上去有点复杂,但是你大概可以知道该代码包含了两个部分,一个是实在的程序体,一个是用“”引号括起来的部分。这括起来的部分仿佛和整体差不多。
如果用Python语言,那么蒯恩就会超级简单:
s = 's = %rnprint(s%%s)'
print(s%s)我们运行这段程序,就会发现它在屏幕上把这段程序自己的源代码打印了出来。仔细分析这段Python代码,就会发现它包括两句话,第一句话同样是定义了一个字符串,字符串的内容简直就是整段程序的包含,只是并不包括字符串这部分。第二句话是打印语句,%的意思是用%后面的变量来替换%前面变量中所有出现%号的地方。但是,%%就表示一个%,并没有替换。于是,运行这段代码就可以实现打印自己的源代码了。
Kleene第二递归定理
不要小看这个蒯恩技巧,有了它,我们就能构造这样一类神奇的程序:运行该程序的结果就相当于将它自己的源代码拿过来做任意的操作。比如,刚才说的Quine就是这样一种将自己的源代码打印出来的一种程序。除此之外,我们还能构造出测量自己源代码长度的程序,运行完程序,它就输出了自己源代码有多长。我们需要做的无非就是在Quine程序的字符串内部和程序本身都附着一段求任意字符串长度的代码就可以了。事实上,计算数学很早就证明出了一个叫做Kleene第二递归定理的结论,说的就是这种程序的存在性。
有了这个定理,我们就不难构造出自我模拟的程序了。我们只需要在Quine的基础上再附着上一段通用程序模拟器的代码。这样,根据第二递归定理,只需要运行这段程序就能模拟它自身的运行了。
推荐课程
本系列课程完整地介绍了通用人工智能(Universal Artificial Intelligence)的基本理论,指明了包含哥德尔机的详细解读,哥德尔机的架构,可实现性和存在性问题。

http://campus.swarma.org/gpac=123

推荐阅读

集智QQ群|292641157
商务合作|zhangqian@swarma.org
投稿转载|wangting@swarma.org
◆ ◆ ◆
搜索公众号:集智俱乐部
加入“没有围墙的研究所”

让苹果砸得更猛烈些吧!
始发于微信公众号: 集智俱乐部










