导语


北京时间2021年10月5日，三位科学家（Klaus Hasselmann，Syukuro Manabe，Giorgio Parisi）因其“对理解复杂物理系统的开创性贡献”获得2021年度诺贝尔物理学奖，复杂系统研究走入大众视野。作为致力于研究复杂系统及其背后统一规律的学科，复杂性科学是集智俱乐部长期关注的核心领域，其基础理论及物理系统等各类复杂系统研究层出不穷。2021年诺贝尔物理学奖再次肯定了复杂系统研究的价值。


诺奖颁布的同时，诺贝尔奖委员会在官网提供了一份15页的文档，详细梳理了三位学者的相关工作，讨论了他们对于理解复杂系统的开创性贡献，并揭示复杂系统理论和跨尺度通用方法对解决气候变化等全球系统性问题的重要意义。集智编辑部组织翻译诺奖委员会评述的全文，以飨读者。


集智俱乐部自12月14日起组织为期2个月的「地球系统科学读书会」，探讨复杂网络、深度学习等方法在气候环境等地球系统问题中的应用，欢迎感兴趣的朋友报名参与，详情见文末。

研究领域：非平衡系统、多尺度结构、混沌、非线性、噪声、随机过程

诺奖委员会 | 作者

王百臻、郭铁城、Leo、梁金、刘培源 | 译者

邓一雪 | 编辑


目录：

I. 引入

II. 气候物理：背景与历史

III. 不同模型的发展

IV. 用观察来测试模型

V. 潜力无限的无序世界

VI. 总 结


   



I. 引入




今年的诺贝尔物理学奖聚焦于物理系统的复杂性，从人类所经历的最大尺度，如地球气候，一直到神秘而又普通的材料中所蕴含的微观结构和动力学，如玻璃。科学家们明白，对任何事物的单一预测都不能被视为无懈可击的真理，如果无法了解可变性的起源，我们就无法理解任意一个系统的行为。例如，直到我们了解了这种可变性的起源，我们才能理解：全球变暖是真实存在的，并且归因于人类。在本文中，我们将从较具一般性的学术背景出发，为讨论这些具体的学术贡献提供一个基本的语境。我们将要关注的一个核心问题这样一个物理现实，即从气候动力学到阻挫材料等一系列基本过程的变化导致了多个空间与时间尺度的出现。因此，这对于理论、实验和观测的解释至关重要。


A. 不稳定性和非线性是多尺度复杂性和随机性的基础


从秩序到无序的涌现，以及随之出现在空间和时间上的多重尺度，是复杂系统的一个特征。理解这种无序的本质是一个艰难的科学挑战。它很自然地包含着以下问题: 这种无序是否会生长？它的时空范围是否是无界的？这种无序会选择一个特定的空间结构，还是许多彼此相异的空间结构？这种选择是否涉及一个系统的所有自由度，亦或是仅仅其中一个子集？如果只涉及一个子集中的情况，那么具体会是哪个子集？


这些问题本身具有与它们所涉及的现象相同程度的多尺度结构。


一个经典的例子是层流向湍流的转变。但是在这个系统以及其他类型的非线性系统中，描述横亘在有序和无序之间的边界是物理学中最具挑战性的问题之一。事实上，多尺度物理学层面的解读已经在湍流的理论和实验方面有了突出的进展。并且我们可知：统计物理学和流体动力学不稳定性之间的联系构成了这个问题一般性的基础。


湍流热对流（例如我们将水煮沸时发生的情况）是一个理想环境，可以用来证明各种尺度在控制热量和质量的宏观输运上所起的作用。当洛伦兹（Edward Lorenz）建立旨在描述大气对流的”玩具模型”时，他就是这样想的。“玩具模型”是瑞利-贝纳德对流（Rayleigh-Benard convection）方程在无应力边界条件下的一个Galerkin截断。模型具体如下：



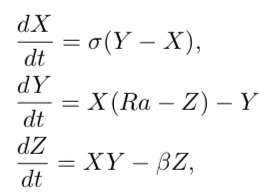
其中X表示对流运动的强度，Y表示上升流和下降流之间的温差，Z表示垂直温度分布的线性偏差。控制参数为 Prandtl 数 σ（流体本身的一种性质）、瑞利数 Ra（驱动垂直流体运动的无量纲浮力）和表征区域几何常数β。


洛伦兹系统是低维混沌中一个经典的玩具模型。鉴于该模型的起源以及其研究的广度是如此广泛，我们很难在这里将这些研究全部列举出来。关于该系统的一个关键事实是：该模型的解是有界的，但它的解表现出了对方程初始条件的敏感依赖性。


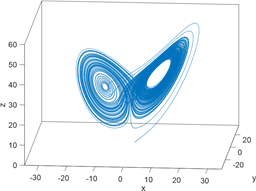
图1. 当人工赋予一组初始参数时，洛伦兹系统电路模拟的相空间图。


庞加莱发现三体问题的长期行为比预期中要复杂得多，并因此被认为是这个领域的开创者。用现代的说法讲，他观察到同宿轨道的缠结（tangling）现象（这是一个动力系统的轨迹，该轨迹将鞍平衡点连接到自身，位于平衡的稳定流形和不稳定流形的交叉点）并推断出运动方程微扰解的发散性。他认识到，太阳系可以被动态地看作是可积开普勒问题的一个扰动。


统计力学和流体动力学中那些令人振奋的远大图景依旧在继续激励并挑战着研究者们。从系统相空间的角度看，原则上，我们可以通过玻尔兹曼、Fokker-Planck或刘维尔方程来获得对系统概率密度演化的完整描述，但这种高维偏微分方程可能难以得到具有实际意义的分析结论。相比之下，低维常微分方程可能会表现出令人震惊的复杂混沌动力学。然而，无论是在抽象形式上还是针对特定的物理系统中，例如那些大气动力学系统，有效的动力学系统可能会在较低维度的低速流形（slow manifold）上运转。因此，我们有理由问出如下这个问题：气候（信号）是否是天气（噪声）的低速流形？当然，这样一个问题是今年获得荣誉的成果中的核心工作，并在更加广泛的非平衡系统中被提出来。在这些非平衡系统中，气候和天气被其他系统所取代。这类问题中的一个关键是，如何区分内部、外部和突发现象。

图2. 对洛伦兹系统赋予两组略微不同的初始参数，从图中可以观察到系统由于对初值敏感而具有发散性，亦可称为蝴蝶效应。


B. 随机性和无序性可推导出可预测性


经典布朗运动假设信号与噪声之间处于均衡关系，并一直处在热平衡之中。然而，在失去平衡的系统中，情况可能截然不同。乔治·帕里西（Giorgio Parisi）强调，平衡系统和非平衡系统之间的区别如下:

“但对于仅仅只是略微失衡的体系而言，情况就不同了。例如，我们可以想象一个系统由于高自由能障碍（可能是能量障碍或熵障碍）而无法达到平衡态：这种情况通常适用于无序系统，如自旋玻璃和结构玻璃。这样的系统将从一个亚稳态跳跃到另一个亚稳态，从而慢慢接近平衡态。如果系统不断受到缓慢变化的外场干扰，它可能永远保持轻微的失衡状态。在这样的系统中，我们可以预期系统的微观时间尺度（例如单个原子的振动）和跨越障碍所需的宏观时间尺度（例如系统本身结构的变化）之间会有着许多不同数量级的分层。我们可以进一步认为：该系统基本上是在亚稳态内热化的，因此仍然可以应用涨落耗散的思想：缓慢变化的系统总体状态被认为是一个小扰动。”


这种基本的思维模式是今年被认可工作的主要特征，无论是对于自旋玻璃，还是对于其他任何复杂的随机多尺度系统（例如气候）。事实上，至关重要的一点是理解以下事实：噪声和无序性能够影响所有系统，并且能全然决定一些非线性动力系统的命运。因此，当噪声引起可变性的根本原因被忽略时，什么是可预测性也就变得似是而非了。


   



II. 气候物理：背景与历史




自从傅里叶 (Fourier) 开始研究地球的能量耗散与吸收以来，我们就知道短波太阳辐射是气候系统的主要能量输入来源。输入主要在可见光波段，输出在红外波段，光谱的这种偏差决定了任何一个大气吸收红外线的行星的宜居性。Eunice Foote 测量了二氧化碳 （CO2）和其它气体对太阳辐射的吸收而导致的加热效应。1861年。John Tyndall 进一步发表了一个精彩的工作[109]，系统地总结了包含水蒸气和二氧化碳在内多种气体对红外辐射的吸收与辐射。这为未来“温室气体”的研究提供了实验基础，同时也是 Svante Arrhenius [6]（1903年诺贝尔奖获得者）于1896年取得重要进展的一个关键因素。我们会在下面谈论更多关于Svante Arrhenius的工作。


除了气候物理学中其他起关键作用的物理因素，地球大气对红外辐射的吸收与出射是物理学与计算方面极具挑战的一个研究领域，与行星物理具有广泛的相关性 [91] 。Archer 和 Pierrehumbert 收集文献中的主要观点，并描述了物理气候科学的历史 [4] 。确实，我们现在可以轻松地在线运行辐射转移模型 (radiative transfer model) ，这种操作的便利程度可能让 Tyndall 感到震撼。我们会在下文介绍辐射转移模型。


图3. 纵轴为红外能量通量，单位是Wm-2，横轴为波数，单位是 cm-1。光滑曲线为在不同温度下的理论黑体辐射谱。图中锯齿形状曲线代表从大气上方到地球的红外光谱。这个模型演示了对波数敏感的温室气体对地球出射红外能量通量的影响。这里考虑一个极端情形，大气二氧化碳从0 ppm（最上方子图）增加到1000 ppm（下面两个子图）。（1）在最上方子图中，大气中不含二氧化碳，出射稳态通量为249 Wm-2。（2）在中间子图，大气中分布着1000 ppm 二氧化碳，吸收使得曲线出现“被咬掉一口”的形状（由黑色向下箭头标识），红外能量通量降低到223 Wm-2。（3）在最下面子图中，为了重新建立249 Wm-2的稳态，在旁边出现“翅膀”（主要是水蒸气，由黑色向上箭头标识），必须在更高温度辐射，地表温度因此增加8.5°C。可以从 http://climatemodels.uchicago.edu 获得在线模型。


图3展示了中等分辨率大气传输（MODTRAN）模型的结果。MODTRAN 模型模拟了地球大气红外辐射的出射与吸收。当大气中二氧化碳增加，逃逸到空间中的红外辐射在谱中间区域降低（如中间子图所示）：波数为650 cm-1的位置像是被咬了一大口，这正是由于行星向外辐射通量降低所致。水蒸气主导波谱直到大约500 cm-1，然后在更大波数再次主导。在大约1050 cm-1位置处出现的更小的被咬掉一口的形状是由于臭氧。为了建立稳态能量平衡，在这个位置两侧、由水蒸气主导的形状像“翅膀”一样的区域，必须在更高温度辐射。在这个例子中，地表温度增加了 8.5°C。


图3中所看到的谱提示我们，地球大气中最强劲的温室气体是水蒸气，而水蒸气的分布是我们无法控制的，我们不可能“控制”雨何时何地降落以及具体降水多少。其实，复杂的水文循环在控制大气中的水蒸气，基础热力学已经证明，温度每上升 1 度，大气中就可以多承载大约 7% 的水。这就是所谓的水蒸气反馈 (water vapor feedback) 。随着行星变热，大气中的水蒸气含量增加，进一步使得温度增加，如此反复递进，温度不断上升。通过水文循环的作用理解水蒸气的分布是一项巨大挑战。


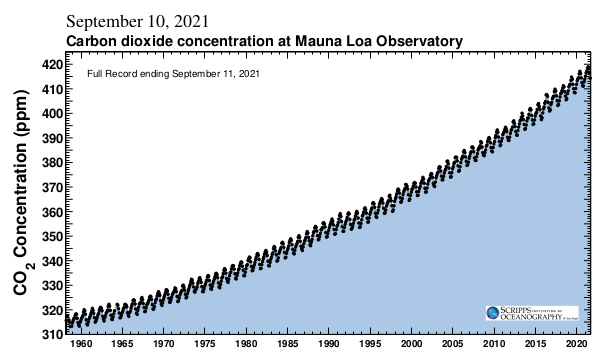
原则上，我们可以通过控制其它温室气体的含量来控制地球的温度。很容易想到的简单问题是：大气二氧化碳的增加会对全球物理气候学带来什么影响？正如物理科学中大多数看似清晰的问题一样，通往答案的路径是曲折的，成功往往与失败和错误相伴。图4的基林曲线 (Keeling Curve) 展示了主要观测结论。该曲线是标志性的，不仅具有分析精度，而且蕴含着有价值的预示信息。在过去8个冰川期中——大约80万年——二氧化碳浓度从未高于300 ppm，在冰川期-间冰期的最大变化为大约130ppm，温度反常大于10度 [25] 。在曲线中包含如此多锯齿的情况下，我们应该如何建立一个模型来描述这样一个系统呢？


图4. 基林曲线是以后来的 Charles Keeling 命名的，此观测项目是 Keeling 开始的。图中曲线展示了莫纳罗亚火山于 1958-2021 年每月的平均二氧化碳浓度。（数据来源为斯克里普斯海洋学研究所；https://keelingcurve.ucsd.edu .）


   



III. 不同模型的发展




A. 能量平衡模型（Energy balance models）


对气候系统而言，太阳的能量输入是最大的外部年度周期性热驱动来源。鉴于此，我们现在知道：任何关于气候的数学理论必须依赖于含时微分方程，来捕获气候子系统在许多时间尺度上的时间演化。另一方面，数值建模推进了天气预报模型中整个系统的耦合方程，可以各种各样的方式将含时驱动力包含进来。显而易见的是：大气、海洋、冰冻圈、陆地和生物圈必须遵循热力学定律。然而，全局耦合系统中大量的时间尺度，使得确定一个给定时间尺度上某个子系统处于何种平衡成为一个很大的理论挑战。


一类标准的能量平衡模型是 Budyko-Sellers 模型 [15, 28, 78, 101] 。每一年从全局平均的角度来讲，可以写出下面这个公式



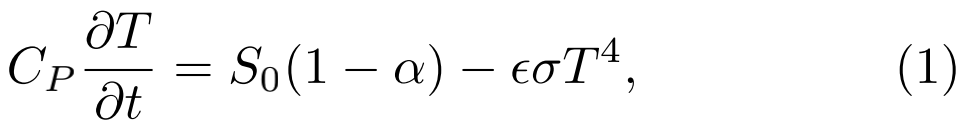
其中 T 为地表温度， Cp 是有效热容，S0和 α 分别为太阳短波辐射通量和表面反射率，σ 为 Stefan-Boltzmann 常数，ε 为辐射率。这个简单模型的不动点为



即入射太阳通量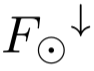与向上地面通量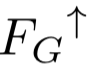平衡，这给出稳态温度。大气的影响在该结果中只体现在行星反射率 α 上。卫星确定 α 近似为 0.3，这包括了高反射的云层（达到0.9）和吸收的海洋（0.2）。因此，TBP不包括大气的红外贡献，也因此不包含温室效应。该温度也经常被称为“裸行星”温度（bare planet temperature），比真实温度要低，TBP≈-15°C [5, 91] 。


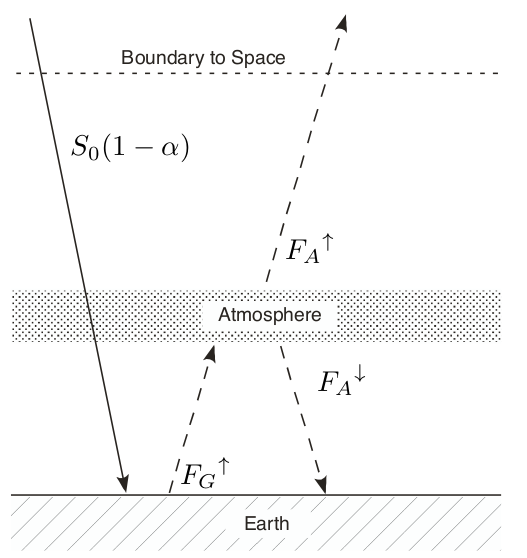
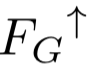图5. Svante Arrhenius在1896年所做的近似[6]，地球上的“单层大气”吸收和释放地表的红外辐射。我们假设大气出射和吸收的红外辐射相等，而且大气是等热的，所以有。（修改自[5]）


图5展示了能够看到大气红外效应最简单的方法。在稳态下，保持大气层通量的平衡，可以推导出以下公式：FG=2FA，以此作为地表的情况，我们可以得到在大气上方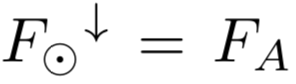。两个关键结果是：（a）大气上方以（冷）裸行星温度 TA=TBP 向空间辐射，（b）地表温度比较温和。


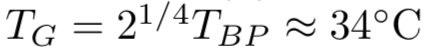将此推广到N层大气，可以发现 TG=(1+N)1/4 TBP。大气上方向空间辐射的温度为TBP。这显然是不考虑温室效应的，忽略了温室气体的谱吸收、反馈以及许多其它效应。这些主导的低阶过程被博学的 Svante Arrhenius 所理解。1896 年，在关于二氧化碳的吸收如何影响TG的开创性工作中 [6] ，Arrhenius 建立了大气柱模式（atmospheric column models，仅包含垂直方向变化和时间演变）中居于核心地位的科学框架，在后续日益复杂的处理中不断得到应用。


现在所知的带饱和 (band-saturation) 效应也是 Arrhenius 所理解的。他利用当时最新的关于二氧化碳和水蒸气的谱数据，特别是 Tyndall 所做实验的数据 [109] 发现，在低气体浓度（或压力）下吸收随着温度线性增长；但是随着浓度上升，所有进入大气的红外辐射都会被吸收。Arrhenius 不仅确定大气不会饱和，并通过现在的谱测量表明二氧化碳还远远不饱和 [91] 。此外，我们现在还知道，由于气体浓度和温度的垂直结构，即使大气饱和，TG仍然可以上升，因为辐射会从未饱和的稀薄上层逃逸到空间中。最后，Knut Ångstrom 争论二氧化碳增加对辐射没有太大影响，因为水蒸气会吸收由于二氧化碳浓度上升而要吸收的红外辐射。尽管这个效应对低层、湿度极高的热带大气起作用，二氧化碳还是会影响与向空间辐射的冷的上层大气相关的红外谱部分。因此，Ångstrom 的论据是多余的 [4, 91] 。


Arrhenius 的预测现在被称为“气候敏感度”，是为了估计当大气二氧化碳浓度加倍时，地表温度 TG 会如何变化。现在的估计范围为2.5-4°C，Arrhenius 预测为大约6°C。这种差别是由于当时吸收谱精度的限制以及图5中对大气模型的粗糙描述。随着现代光谱学的发现，由于前文所述效应——二氧化碳影响与上层冷大气相关的辐射到空间的红外谱范围——没有被包含进来，所以导致后面的近似低估了气候敏感度。这种低估被他所用的谱数据所修补。


Arrhenius 也关注现代物理气候学的其它重要部分，特别是赤道-极点能量不平衡和冰反射率反馈 (ice-albedo feedback) 。对于后者，在式(1)中反射率与纬度相关意味着，气候系统最基本的两个状态——冷和热——与北极快速演化的冰块紧密相关。确实，他对冰期的二氧化碳浓度做出了完美的预测：预测数值为 150 ppm，而从冰芯研究 [25] 可以知道二氧化碳浓度为180-200 ppm。他也对人类燃煤消耗如何导致大气二氧化碳浓度加倍做出估计。所有这些都包含在 Arrhenius 的一篇文章中，他在其中为现代以各种不同形式使用的大气柱模式提供了概念框架。从这种意义上说，人们知道温室气体对气候的影响已经有一又四分之一个世纪了。Arrhenius 的工作是伟大的预知，并且为今天的分析提供了基本要素。可以参考 [4] 中的讨论。


B. 广义的确定性能量平衡模型（EBMs）


正如在§III A小节所介绍的那样，最简单的模型处理整体平均，主要关注大气的辐射转移特性。这些推广到每年平均、地区（跨过纬度方向地带）平均的量，引入纬度依赖的TG、α和子午线方向（经线方向）热输运。这个框架含有时间依赖的行星冰线以及空间冰反射率反馈。如果扰动使得冰盖扩张，系统吸收的能量变小，由式(1)得到它会更快地变冷，冰继续扩张，这将驱动变冷的反馈过程。确实，这个理论预测，只要当太阳辐射通量 S0 低于几个百分点时，就会急剧转变到一个完全冰覆盖的地球，一个“雪球”。一种解析方法 [79] 可以找到三个不动点；雪球和间冰期（当下的状态）都是稳定态，近似三分之一冰覆盖则是不稳定态。对于这类理论可以利用谱方法求解，正如数值求解 Navier-Stokes 方程所用到的谱方法 [77] 。


尽管人们很早就得到冰河时期清楚的观测证据 [2] ，一系列 EBMs 模型所预测的多种全球气候状态却被看做是不真实的理论预测。然而，现在对“核冬天”——核武器引起的烟尘阻挡太阳辐射——的关注也成为了他们预测的兴趣。直到最近几十年人们才发现大约 7亿年前的新元古代时期发生的冰川作用 [54, 100] ，这也体现了 EBMs 模型 [15, 101] 作为定量工具所发挥的作用。


重要的是，这些理论捕获了气候系统的很多可能的态，并且包含很多出现在不同物理问题中的数学上有趣的推广的特征。正如 §III D 小节所展示的那样。从这一层意义上来讲，气候科学促进了其他物理领域的研究。


C. 数值气候模型的出现


1. 序曲


所有的模型都是对现实的近似。近似也就意味着，不管是数学解析还是对公式的数值求解，都会在特定的极限条件下失效。科学的艺术就在于对现实给出合理的近似，只有明确了模型失效的精度，我们才可以定义所谓“严格”。因为大型计算设备的获取日益方便，气候科学中“模型”一词几乎等价于全球气候模型 (Global Climate Models, GCMs) ，而不是 EBMs 。当代的 GCMs 将大气、海洋、冰系统参数化并表示为次网格尺度（sub-grid scale）的物理过程（比如 [38] ），通过数值求解质量、动量和能量守恒来进行处理。一些现代的方法利用数据同化 [94] ，测试高分辨率机制 [52] 来改进 GCMs 模型。


由于气候（特别是流体）系统的复杂本质，GCMs 是目前发展的最复杂先进的数值模型。尽管如此，完全解决气候系统中的时空过程依然是一个挑战，特别是对于高纬度位置 [1] 。因为 GCMs 模型的复杂结构和处理的高维数据，抽取不同时间尺度上的主要物理过程并不是很直接，也无法解释它们之间的相互作用。因此，GCM 像是巨大的粗粒化的天气预报模型；全球气候由所有已知物理过程和次网格尺度过程参数化的计算近似结果所代表。气候模型的最新进展系统地包含了克劳斯·哈塞尔曼（Klaus Hasselmann）最早发展的概念 [42] ——天气的混沌动力学带来长时间尺度的变化，这必须包含在模型中 [11, 20, 29, 59, 80, 81] 。


2. 起源


入射太阳能与出射红外能量的差是关于纬度的函数，在40°N和40°S之间有 5PW （千万亿瓦）的超出。能量通过大气和海洋的运动传输到高纬度地区。因此热量的大小和分布与旋转系统中流体的运动和混合紧密相关。大气承载着 5PW 能量的三分之二，剩余的由海洋传输，但是在不同时间尺度，并且受地理环境影响。因此理论与模型在现实中受制于这些因素，并且由于冰反射率反馈的原因，冰冻圈也会受到影响。


1950年，普林斯顿高等研究院的 Jule Charney 和冯·诺依曼 (John von Neumann) 领导了一个大规模数值天气预报项目 [19] 。这自然地与研究大气和海洋动力学的细致过程的理论和实验研究——地球物理流体动力学 (geophysical fluid dynamics, GFD) [114, 115] —— 同时发展。随着时间发展，GFD、天气预报和气候建模之间存在文化差异，并且产生了不同学派，尽管方法不同，但它们都有共同的目标。


包括 Bert Bolin 在内的很多先驱都被招募到这个项目中来，或者来访问，为这个项目带来了专家经验 [112] 。这里的关键是美国气象局大气环流实验室的负责人 Joseph Smagorinsky 的参与。他后面去到了普林斯顿地球物理流体动力学实验室，并在 1959 年招募了真锅淑郎（Syukuro Manabe），1961 年聘请了 Kirk Bryan。实验室很快聚集了大量程序员。


直到 1960 年 Cecil E. Leith 独立开发了现在公认的第一个完整的仅针对大气的 GCM (AGCM) ，历史细节可以在最近的一篇文章 [39] 中找到。该模型包含更低的平流层，以及对水文循环和云的表示。Leith 给出程序运行的演示，并且站在计算机可视化的前沿。


3. 关键结果


数值模型 [61-63] 基于固体物理，并且可以看做 Arrhenius 设想的首次实现。更早的重要研究 [60, 75] 关注如何将已知的动力学和辐射过程包含进柱模式 [62] 。


真锅淑郎和 Wetherald [62] 将整个大气视为一维的柱，包含特定的相对湿度和温室气体浓度。从初态系统演化，通过（a）辐射转移，这可以通过温室气体的谱进行计算，其中占最重要权重的是水蒸气；（b）对流调整，这个过程对垂直动力学进行如下参数化。如果一个柱仅通过辐射转移演化，衰减率为~-15°C/km，远远大于观测值。现在，绝热衰减率为~-10°C/km，但是在大气中随着空气升高水凝结会释放潜热，这解释了观测到的“湿润”衰减率~-6°C/km。为了对该现象进行建模，只要温度与湿润衰减率有所偏差，表面加热便会驱动垂直运动、相变和与之相伴的热释放。这就是真锅淑郎和 Strickler [61] 的对流调整机制。


真锅淑郎和 Wetherald [62] 注意到，北半球的气候纬度相对湿度的数据几乎没有季节性依赖变化，而绝对湿度（饱和蒸汽压）敏感地依赖于温度。因此，他们 [62]重复了真锅淑郎和 Strickler [61]的计算，关键的区别在于后者（更早的）文章使用了相对（绝对）湿度的分布，很好地捕获了上面所讨论“水蒸气反馈”。正如图 5 的注解所述，大气上层辐射到更低温度的空间，为了使能量平衡，必须捕捉相对湿度（包括最重要的温室气体）、其他温室气体的浓度和温度。这种汇集效应导致真锅淑郎和 Wetherald [62] 所给出的重要结果，即大气二氧化碳加倍导致 2.3 °C的变暖。


1975年，真锅淑郎和 Wetherald [63] 通过求解全球热、质量、动量和辐射的耦合方程，很大程度改进了他们 1967 年的计算 [62]，这是他们的第一个GCM，当时利用的计算机是大约 0.5 MB 的 RAM。当二氧化碳从 300 ppm 加倍到 600 ppm，全球平均表面温度增加 2.93 °C。模型假设无海洋热输运、理想化的地形，以及云层固定分布。


正如 §III A 小节所描述的那样，Arrhenius 引入了气候敏感度的概念，这一概念直到今天依然发挥作用。然而，我们需要区分 Arrhenius 的概念，或者说区分平衡气候敏感度（ECS）与瞬时气候敏感度（TCS）的差别。ECS 预期二氧化碳立即加倍，然后计算新的稳态能量平衡，但达到稳态所需的时间几乎完全不准确。对于一个极端情形，大气二氧化碳从 0 ppm 增加到 1000 ppm ，如图 3 所示，其中中等分辨率大气传输模型 (MODTRAN) 模型被用来展示 ECS 的思想。MODTRAN 使用与真锅淑郎和 Wetherald [62] 同样的方法，来模拟大气中红外辐射的出射与吸收，但是是利用现代的谱数据与方法。当二氧化碳释放到大气中，逃逸到空间的红外辐射在中间谱段减少，这可以从中间子图看出来。但是为了重新达到稳态，它旁边的“翅膀”（水蒸气占据主要作用）意味着必须在更高温度辐射，因此地面温度会升高 8.5°C。该计算重新平衡了柱能量，正如真锅淑郎和 Wetherald [62, 63] 所做的那样，并且需要新的地面温度来实现这一点。


当代 GCM 产生的气候敏感度区间在 2.5-4°C，真锅淑郎和 Wetherald 的两个不同方法[62, 63]给出 2.3-2.93°C的结果。正如 §III A 小节所述，我们知道 Arrhenius 关于 ECS 的结果（大约6°C）为什么是上限（吸收谱精度和等热大气），但是真锅淑郎和 Wetherald [62, 63] 结果的鲁棒性是显著的，这也预示着增加模型复杂度并不一定会提高模型的预测能力。实际上温室气体是随时间演化的，气候的响应也是如此，这是 TCS 所蕴含的。因此，瞬时气候敏感度（TCS）确实影响着人类。ECS 和 TCS 都是模型依赖的，正是 Hasselmann 建议了一种机制来系统地评估模型与变化的观测量相比到底如何，以及是什么引起了两者的变化。


D. 随机理论 （Stochastic Theory）


行星大气体现了在不同时间和空间尺度上的相互作用。短波辐射通量的空间不均匀性驱动大气和海洋的流体动力学，通过流体对流和波传播 [31] 导致长程联系。上面所述的 GCMs 尽量包含这些过程，但是大量计算来量化这些变化是持续的挑战。因此如何从统计的中心极限定理的角度来量化可变性在观测和理论研究方面都引发了浓厚的兴趣。在这同一时期，真锅淑郎和合作者们的确定性模型（deterministic model，不包含任何随机成分）主要专注于构造 GCMs 模型。


考虑全球 Budyko-Sellers EBM ，比如式(1) 。假定真实地面温度 T 与平均地面温度 TS相差不大，因此 T=TS+x，|x|<<|TS| [73]。高频涨落（如与天气相关的涨落）可以用白噪声η(t)表示，具有常数振幅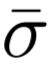，因此 x 的时间演化由过阻尼 Ornstein-Uhlenbeck 过程，或者广义朗之万方程表示：



其中


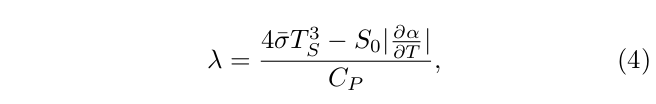
这里 λ 表示相对于平衡温度TS的整体气候确定性稳定度。反射率敏感度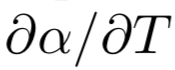为负，提供正反馈，而向外的长波辐射通量的敏感度为正，可以稳定对TS的偏离。


信号处理领域关于压强场 [76] 的谱特性的观测分析，促使 Mitchell [71] 利用自治郎之万方程（autonomous Langevin equation，自治系统通常表示其中的物理规律不随时间变化）对海洋气候的描述。同时 Hasselmann 创新性地利用基本物理概念来量化表面海洋波谱 [40, 41] ，从而深入了解海面的波动性质。基于这项研究的直觉，以及湍流和洛伦兹混沌天气中的基本概念，他推导出对海洋气候的推广的随机描述，其中“噪声”与上面描述的“天气”有关 [42] 。他的工作为气候科学家研究气候变化提供了动机和观测结构。


1. Hasselmann 随机框架简述


这里我们为 Hasselmann 随机框架[42]提供一个简单的解释。考虑所关心的气候系统可以用矢量 x=(x1,…,xi) 和 y=(y1,…,yi) 表示的一组耦合的控制方程描述，由两组函数 fi 和 gi 控制，如下



其中所有xi的演化的特征时间尺度都比yi的演化特征时间尺度短。后者描述“缓慢”演化的大尺度气候观测量。不失一般性的，我们进一步简化所考虑的情形，考虑x和y为标量的情况，这样我们就可以通过快变量（fast variable）x写出y的有效动力学 x=<x|y>+x*，其中 <x|y> 为条件平均，x在状态y的条件下的平均。因为x比y变化更快，我们利用条件动力学



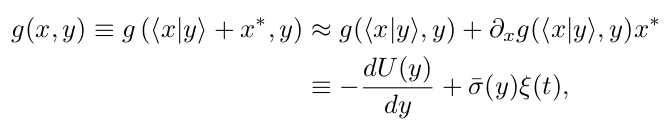
其中我们假设快变量的迅速变化 x*(t) 可以由白噪声来近似，σ(y) 为依赖于慢变量y状态的振幅，因此确定性动力学可以表示为势 U(y) 的拖曳力。最后，当噪声强度很小时，系统会在一个不动点（如 yE）附近待较长一段时间，在这个不动点附近，拖曳力可以展开，并且噪声振幅看起来是常数。然后气候变量 y(t) 的动力学便约化为具有式(3)形式的 Ornstein-Uhlenbeck 过程，



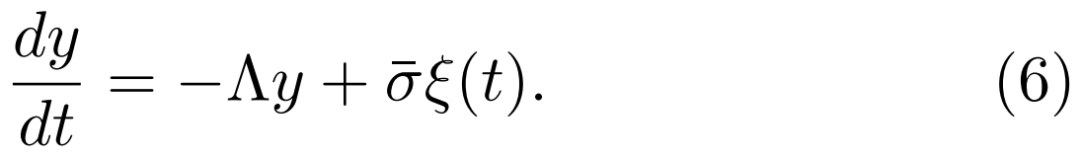
通过布朗运动概念处理问题，使得我们可以利用随机微分方程框架研究气候变量。比如，除了通过式(6)研究系统的状态，我们还可以研究系统在特定时间处于特定状态的概率，因为对于任何一个朗之万方程都存在一个 Fokker-Planck 方程 [22] ：这是对解释气候观测非常有用的框架。此外，式(6)的解给出自关联函数（auto-correlation function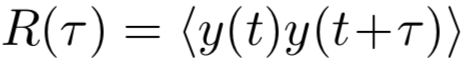），，它的傅里叶变换给出功率谱，



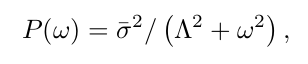
表明（a）式(6)中的白噪声过程的红噪声响应，（b）涨落耗散定理的最基本形式，将噪声强度与过程的方差联系起来，即



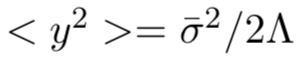
需要强调的一点是，不同于 Mitchell，Hasselmann 并不是直接利用式(6)作为观测启发的拟设。他从式(5)出发，而这更适合作为气候模型的随机参数化框架 [11, 20, 29, 59, 80, 81] 。重要的是，在气候动力系统中有大量的时间尺度，对时间尺度进行清晰区分对于理解现代气候变化至关重要 [29] 。Hasselmann 方法的关键是上述确定性的平均，给出一个快-慢耦合的确定性系统，由平均力的噪声修正控制。正如 Culina 等人所述 [20] ，这一点直到最近才被严格地证明，但是是在比 Hasselmann 考虑情形更严格的条件下。


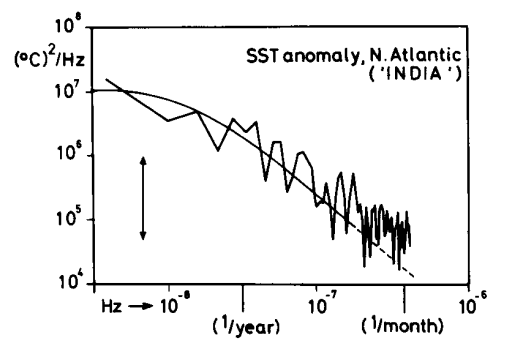
图6. Hasselmann 随机模型 [42] 用于气候数据 [26] 进行气候变化研究的第一个应用。1949-1964年北大西洋海面温度 (Sea Surface Temperature, SST) 谱。95% 置信区间由图中双向箭头表示，Λ-1 =4.5 月。


在图 6 中，尽管随着频率减小，谱不断增长，但因为有限耗散 Λ 的存在，我们期望它最终会达到饱和。然而，Hasselmann、Wunsch [113] 以及其他人指出，海洋对时间有极其长期的记忆，可达成百上千年。此外，在与人类相关的几十年时间尺度上，得到的证据与记忆时间无穷长时是一致的。因此，这表明存在一种可能的自相似或分形特征，不同时间尺度提供不同类的随机过程（例如白噪声、粉噪声、红噪声等） [72] 。因此一个数据记录是不稳定的态，具有变化的方差和不易测量的平均值，是 Hasselmann 类比布朗运动的工作中体现出的气候变化的基本特点。


显然这种方法可以推广和应用到其他领域的很多方向去。然而，将气候数据，以及气候可预测性和变化视为随机过程的理论框架可以追溯到 Mitchell [71] 和 Hasselmann [42] ，后者成功将随机方法应用到图6中来自 Claude Frankignoul 的数据中。正如很多好的想法一样，新的方法和想法可以从中产生，但它也有很多近似和限制。特别的，如上所述，识别出观测数据中不同的谱隙可以证明时间尺度分离的假设，但这依赖于所使用的数据。


尽管如此，由于 Hasselmann 的理论， 对于气候变化的典型的零假设是红功率谱（红噪声对应的功率谱，高频减少，低频权重更大） [65, 113]。


   



IV. 用观察来测试模型




从实验室科学的角度来看，使用实验测量来检验理论是科学方法中不言而喻的一步。然而物理宇宙学（physical cosmology）和物理气候学（physical climatology）是观测科学——研究者观察到的是自然所允许观察的。


在卫星时代前的几十年，理解大气和海洋的动力学依赖于稀疏的观测。例如在国际地球物理年（1957-1958）之前，当大规模系统观测计划启动时，大部分理论和观测重点都集中在诸如两极 [58,110]之类的区域，或是诸如墨西哥湾流之类的洋流行为，以及普遍的海洋和大气环流理论（由Jacob Bjerknes，George Carrier，Walter Munk，Carl Rossby 和 Henry Stommel等人的理论推动）。这些问题突破了数学和数值建模的界限。事实上，§III C中讨论的普林斯顿高等研究院的数值预测小组，其成立的部分原因正是由于缺乏观测数据。


正如1922年诺贝尔物理学奖得主尼尔斯·玻尔（Niels Bohr）所言，“预测是非常困难的，尤其是关于未来的预测！”我们了解未来气候的主要工具是由真锅淑郎和他的同事们开创的 GCMs。人们预测，或者用该领域的术语说“设计”（project），然后等着看会发生什么。当然，未来将永远等待我们到来，但Hasselmann 的想法是通过模型和观测来探究，是什么情况导致气候达到了当前状态？是自然变化还是人类活动导致了温室气体浓度增加？


A. 气候的指纹识别


为了评估气候模型是否忠实再现了自然变化的信号，Hasselmann对随机气候动力学的兴趣自然而然地导致他创建了一个框架，来系统地比较气候模型和观测结果。这项工作体现在了 1979-1997 年发表的三篇论文 [43-45] 中。


Hasselmann在该系列的第一篇论文[43]中指出，尽管概念上类似于单一网格点的数据，但处理气候信号的矢量场结构仍是一项挑战。也就是说，在引用单一网格点的方法时，“响应模式作为整体或部分是否具有统计显著性的问题，显然无法通过这种方法解决”。他的工作提供了从纯空间数据 [43] 到空间-时间数据[44,45] 的框架。重要的是，他展示了最优检测技术如何揭示对气候系统自然变异性或者“噪声”本质的理解。也就是说，信号的检测不一定与信号最强的部分数据有关，而是与噪声最弱的数据部分有关，从而揭示出对系统各组成部分更加细致的物理解释。


指纹识别（fingerprinting）方法通过使用气候模型运行，基于控制系统的物理学来识别气候变化。所谓的最优指纹（optimal fingerprinting）方法是对多元回归的时空泛化，适用于气候变化检测和将变化归因于外部强迫气候信号。时空指纹（spatio-temporal）识别方法，例如温室气体浓度随时间的三维变化，提供了区分观察到的变化和自然变化的手段。经过多年的改进[45-49]，该程序远比模型模拟与单独观测的比较更加严格、细致和全面。


一个从由向量y给出的观测记录的过滤版本开始，回归采取标准形式y=Xa+u，其中矩阵X包含外部强迫或信号的估计响应模式，a是调整这些模式振幅的比例因子向量，u表示内部气候变异性，通常假定它是一个具有协方差矩阵c的高斯随机向量。矢量a是用各种统计技术根据c、X和y估计出来的，其中X包含使用GCM模型或EBM模型所估计的信号，以创建具有复杂时空结构的“内部可变性”（internal variability）。要想将观测到的反应归因于人为强迫，X必须包含单独的自然和人为响应，因此必须说明强迫调整振幅以将模型与观测结果相匹配的可能错误。通过这种方式，检测和归因是通过物理推理和评估关于a中的比例因子的具体假设来确定的。重要的是，结果依赖于对观测结果的准确指纹振幅的估计，并且与所使用的气候模型是否正确地模拟了指纹振幅无关 [例如49] 。


在最近的一篇“庆祝气候变化科学三大事件的周年纪念”文章中 [98]，Santer和他的同事们回顾了自1979年《查尼报告（Charney Report）》[19] 以来的40年间取得的进展，报告与Hasselmann关于“如何自洽地比较模型和观测结果”的论文 [43]同年发表。Santer文章共有4个部分 [98]，第一部分是查尼报告的摘要，第二部分是Hasselmann最优检测的论文 [43]——作者称之为“为确定人类造成的变暖信号提供可靠统计框架的首次严肃的努力”。这种方法与以往的单变量统计工作不同：


Hasselmann没有选择大海捞针然后去下个地方继续捞，而是提倡一种更高效的测量——同时搜索整片大海。他还指出，理论、观测和模型提供了大量有关信号和噪声的适当联系的信息。这些独特的信号特征（或指纹）可以用于区分气候信号和气候噪声。


查尼报告依赖基础理论和早期气候模型模拟，从中人们清楚地认识到化石燃料燃烧将明显产生全球变暖信号[19]。Hasselmann的论文 [43] 概述了检测该信号的合理方法。卫星搭载的微波探测器此后开始检测大气温度，提供全球数十年气候变化模式和自然内部变化信息，这些是应用Hasselmann信号探测方法所需要的。


Hasselmann的论文是后来数百项气候变化检测和归因研究的统计学路线图，为IPCC在2013年得出的结论提供了强有力的科学支持：自20世纪中叶以来，人类的影响极有可能是观测到的气候变暖的主要原因。


   



V. 潜力无限的无序世界




A. 复型、自旋玻璃、阻挫


“自旋玻璃”这个术语是在20世纪70年代初被创造出来的，用来描述无序的磁系统，这种系统会发生相变，结果使得每个磁性原子都具有稳定的排列，只不过排列方向在原子之间随机变化。想象一个三角形，三个角上各放着一个小磁体。磁体的北极可以向上，也可以向下。在直观情况下，假设将三角形置于垂直于其平面的向上或向下的外部磁场中，我们可以想象这三个小磁体都指向上或向下。


现在如果我们施加一个“反铁磁”约束，使得任何一对相邻的小磁体必须具有相反的方向。当两个磁体满足约束条件时，另外两个就无法满足，无论如何翻转磁体都无法满足约束条件——系统遭遇了“阻挫”（frustrated）。这种极端理想化的设置是一种简单的方法，可以用来观察自旋玻璃和其他系统如何遭遇阻挫。

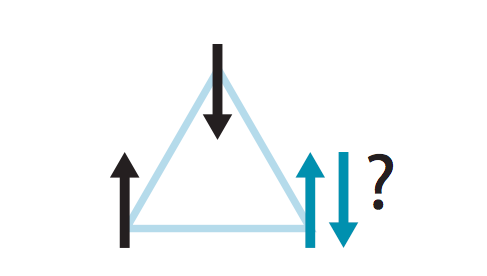
三角形中的反铁磁自旋系统遭遇阻挫


许多阻挫系统都以独特的方式受挫，它们有很多选择，包括“结构”或“普通”玻璃，“边缘”或“Gardner”玻璃。我们并不打算专门讨论各种玻璃系统，只是想强调这类系统的一个共同特征：当迅速猝灭时，它们无法进入平衡态，而是会持续占据大量非常长寿的亚稳态。


因此，一个给定的实验系统通常有一个独特的测量、数字和/或概念协议。从一开始，系统的特殊性就一直是该领域的主要挑战[例如 12, 68, 96]。1977年诺贝尔奖得主菲利普·安德森（Philip Anderson）认为：“自旋玻璃的历史可能是我所知道的这句格言的最好例子，即一个真正的科学谜题是值得追寻到地球尽头的，即使不具有任何明显的实际重要性或智识上的魅力。”（The history of spin glass may be the best example I know of the dictum that a real scientific mystery is worth pursuing to the ends of the Earth for its own sake, independently of any obvious practical importance or intellectual glamour. ）[3]


B. 解决复型的对称破缺问题


为了简便起见，我们可以把自旋玻璃看作是包含杂质的系统，或具有如下哈密顿量的自旋系统：



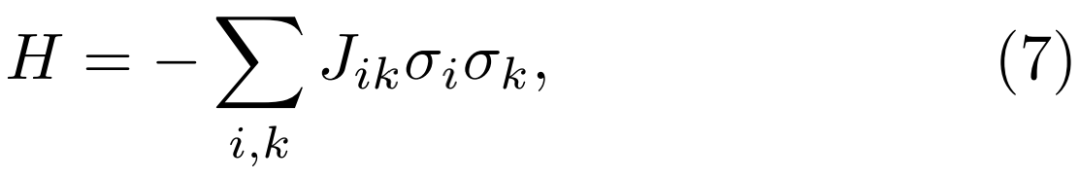
其中，Jik是非关联的高斯随机变量，均值为零，方差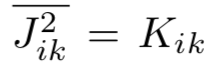由于同时允许铁磁和反铁磁耦合，便会出现阻挫，因此我们预期会出现一个“凹凸起伏”的能量地形图和许多长寿命的亚稳态。在这个框架内，我们可以用启发式的术语来概括发展。Edwards和Anderson[24]考虑一种短程相互作用，Kik随着 i-k 距离的增大而迅速减小。重要的是，他们为自旋玻璃相构造了一个序参量，也就是自旋在其初始方向上的投影，使得我们可以忽略长程空间序而考虑长程时间序。因此，在等待很长一段时间后，如果序参量是有限的，就意味着自旋“记住”了它们最初的指向，在这个意义上也就意味着形成了玻璃态。此外，为了在Jik具有大量不同构型的宏观样本上进行平均，他们引入了所谓的“复型技巧”（replica trick），将配分函数复制 n 次，即，



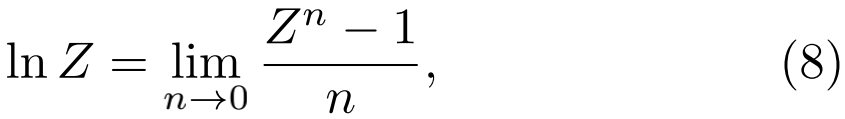
从而允许正确的平均热力学计算，F =−kT⟨lnZ⟩ave。


同年，Sherrington和Kirkpatrick[102]提出了 Edwards-Anderson 模型的无限维版本，也就是 Kik = N-1，其中N表示自旋总数。虽然这使有效的平均场计算成为可能，但也揭示了一个悖论：低温时熵变为负值。由于许多状态具有几乎相等的能量，且没有明确的对称性，计算收敛解是一个巨大的挑战。然而，这一挑战启发了模拟退火（simulated annealing）[53]。紧接着 Thouless（2016年诺贝尔奖得主）、Anderson和Palmer[106]解决了负熵问题，却留下了解的稳定性问题，然后 de Almeida 和Thouless[21] 指出了“复型对称”所假设的问题。这导致 Blandin[13]、Bray和Moore[14]对复型对称破缺的计算，但如何破坏复型对称，其中微妙之处仍然影影绰绰。


Giorgio Parisi 解决了复型对称破缺的问题。他意识到，与铁磁体在有序相中只有两种“纯态”（上/下）不同，自旋玻璃在有序相一定有无穷多个态[82,83]。这不仅提供了解决方案，而且在自旋玻璃和其他系统中具有一系列出人意料的扩展 [68,69,84-86]。


为了实现无穷多个状态，Parisi所做的重要突破是引入一个新的序参量：



其中α和β为复型。所有的qαα都是等价的，表示一个给定复型中状态的平均重叠度，非对角项则度量α和β彼此相似的程度，即它们描述属于复型α和属于复型β的状态的平均重叠度。在玻璃相中，没有唯一的局部稳定热力学状态，而是有许多状态，每一个状态的复型对应平均场方程的一个不同解。这些解是N自旋系统的N维构型空间中的状态集合。


数学超出了我们的讨论范围。其中一个关键概念叫做超度量（ultrametricity），这是我们上学时就知道的三角不等式（三角形任意两条边的长度之和大于或等于第三条边）的泛函版本。在这里，超度量可以用一个描述系统状态的网络来刻画，我们会发现，当随机选择三个状态时，至少有两个重叠是相等的，这样重叠的无序平均分布（disorder-average distribution）是



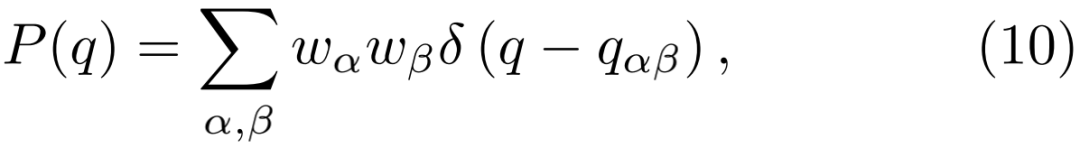
ω 是玻尔兹曼权重。


C. 应用和影响


自从 Parisi 的原创性工作问世以来，复型对称破缺概念和方法的广泛影响爆发式地增长。特别是，Parisi和他的合作者证明，在 John Hopfield 的神经网络模型[50]及其众多衍生模型中，存储在网络中的多重记忆与自旋玻璃的多重平衡相是对应的。


此外，复型方法让我们能够解决旅行推销员这个经典的最优化问题。这个问题说的是，给定一系列城市和每两个城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路，这个问题有许多局部极小值，而求解的目标则是全局极小值/最小值。[68] 在这本书出版的时候，David Thouless写道[107]：


我觉得研究自旋玻璃的专家们就像是在敌对地区扎营的定居者。他们做了一些有趣的观察，但还没有学会如何与那些更早的定居者交流。在一些关于神经网络的论文中，几乎没有提及自旋玻璃社区之外的其他科学家的工作。


显然，在此后的30多年里，早期定居者在许多地方广泛殖民。这包括 (a) 基本理解为什么一些最优化问题很容易，而另一些很困难（见[70]和其中的参考文献），(b) 为结构玻璃提供一个随机的一阶理论，(c) 给出硬球阻塞填充问题的几何理论，这是平均场复型对称破缺的一个极其成功的应用，从二维到无限维都适用[89]。该方法为经典颗粒物质[9]的实验确立了标准，并在平衡和缓慢压缩的详细数值分析[16,17,95]中得到了证实[93]。


此外，在缓慢致密化的胶体玻璃[37]中直接观察到了玻璃复型理论所预测的边缘相（marginal phase）。重要的是，在使用随机激光器[30,33,99,108]的系统中，在没有无序、但相互作用的激光模式之间存在阻挫的平面腔激光器中[7,74]，以及通过光折变无序波导的非线性光传播中[90]，都给出了复型对称破缺的实验证据。


最后，随机激光系统的性质允许对复型对称破缺，以及自旋玻璃和湍流[34]之间的联系，特别是非线性波相互作用进行伴随观测，这将Hasselmann的早期工作[40]与Parisi的理论，以及无序和涨落在一般复杂系统中的作用联系起来。


随机激光和复型对称破缺


如上所述，公式(10)所预测的一阶复型对称破缺的双峰特征的一个激动人心的领域是在随机激光中，其中受激发射以这样或那样的方式被介质复杂化[30,33,99,108]。由于能量密度由泵浦功率控制，泵浦功率与温度成反比，因此，随着泵浦功率增加，系统中的非线性将发挥类似于低温在玻璃形成过程中的作用，让能量地形图变得起伏不平。另一方面，当泵浦功率较低时，腔模表面上相互独立，类似于自旋玻璃的顺磁相。重要的是，随机激光器有大量的亚稳态，而混沌激光器有少量的模式可以表现出指数路径发散。这导致不同类型的激光具有不同的光谱特性。


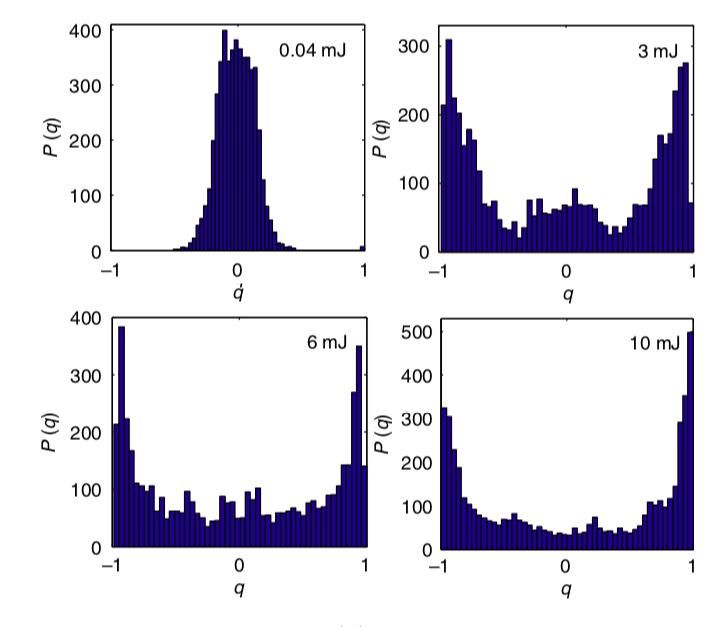
图7. 不同泵浦能量（如插图所示）的qαβ的重叠分布P(q) [30]。如本文所讨论的，泵浦能量与温度的作用相反，随着泵浦能量增加，一阶复型对称的分布出现破缺。


Ghofraniha等人[30]对随机激光的光谱数据进行量化，并分析不同发射之间的涨落。这背后的想法是，每个发射光谱都定义了在相同条件下随机激光的一个复型，比如说α。如果强度涨落函数为，其中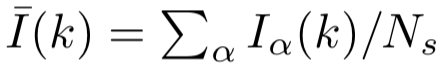是标记为k的每个波长的平均强度，则 Parisi 重叠函数(9)变为



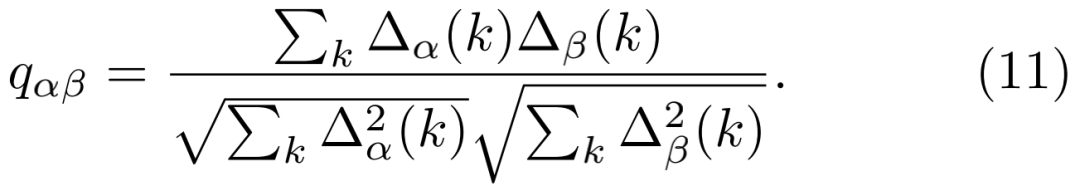
可以观察到，在泵浦功率高（温度低）时，光谱变化要大得多，在特定能量下，发射强度的变化是不连续的，表现出相变（[30]图3）。在产生多次发射后，实现了对P(q)的直接测量，并表现出如图7所示的一阶复型对称破缺。在不同的随机激光系统中发现了相同结果[99]，这说明复型对称破缺在表现中具有稳健性。


我们讨论了复型对称破缺的实现，事实上，Parisi 通过涨落、随机和无序的透镜，揭示并发展了一系列物理系统之间错综复杂的联系，其中包括量子场论中的随机性、湍流的间歇性、欧几里德随机矩阵、玻璃中的非平衡涨落、随机界面运动、颗粒物质，以及随机涨落在控制地球长期气候状态中的作用。


   



VI. 总 结




显然，今年的获奖者作出的开创性贡献，有助于我们理解复杂物理系统的微观与宏观。他们的研究表明，如果没有对无序、噪声和可变性的正确解释，那么决定论就只是一种错觉。事实上，本届诺奖所认可的工作也部分反映了理查德·费曼（Richard Feynman，1965年诺贝尔奖获得者）的评论——相信怀疑是首要的，这不是我们认识能力的缺陷，而是认识的本质（Believed in the primacy of doubt, not as a blemish on our ability to know, but as the essence of knowing）[32]。


这三位科学巨擘的工作表明，对任何事物的单一预测都不能被视为不可质疑的真理；如果不冷静地探索变化的根源，我们就无法理解任何系统的行为。因此，只有在考虑了这些根源之后，我们才能理解——全球变暖是真实发生的事情，其原因也在于人类活动；我们在自然界中观察到的大量现象都来自潜在的无序；而拥抱噪声和不确定是通往可预测性的必经之路。



参考文献


[1] Agarwal S, Wettlaufer, J S. 2018. Fluctuations in Arcmodels. Phil. Trans. R. Soc. A 376, 20170332.
[2] Alley RB. 2000. Ice-core evidence of abrupt climate changes. Proc. Nat. Acad. Sci. USA 97, 1331-1334.
[3] Anderson PW. 1988. Spin Glass I: A Scaling Law Res?cued. Phys. Today 41 526.
[4] Archer D. and Pierrehumbert RP. (Editors). 2011. The Warming Papers: The Scientifific Foundation for the Climate Change Forecast. Wiley-Blackwell, Hoboken, NJ, 432 Pages.
[5] Archer D. 2006. Global Warming: Understanding the Forecast, Wiley 208 pages
[6] Arrhenius A. 1896. On the Inflfluence of Carbonic Acid in the Air upon the Temperature of the Ground, Phil. Mag. 41, 237-275.
[7] Basak, S., Blanco, A., López, C. 2016. Large flfluctu?ations at the lasing threshold of solid-and liquid-state dye lasers. Sci. Rep. 6, 32134.
[8] Batchelor GK. 1953. The Theory of Homogeneous Tur?bulence. Cambridge: Cambridge Univ. Press. 212 pg.
[9] Behringer, RP. Chakraborty, B. 2019. The physics of jamming for granular materials: a Review. Rep. Prog. Phys. 82 012601.
[10] Benzi R, Paladin G, Parisi G, Vulpiani A. 1984. On the multifractal nature of fully developed turbulence and chaotic systems. J. Phys. A 17 3521-31.
[11] Berner J, and 26 others. 2017. Stochastic Parameterization: Toward a New View of Weather and Climate Models. Bull. Am. Met. Soc. 98(3) 565-587.
[12] Binder K, Young AP. 1986. Spin glasses: Experimental facts, theoretical concepts, and open questions. Rev. Mod. Phys. 58, 801.
[13] Blandin A. 1978. Theories versus experiments in the spin glass systems. J. Phys. Coll. 39 C6, C6-1499-C6-1516.
[14] Bray AJ, Moore MA. 1978. Replica symmetry breaking in spin-glass theories. Phys. Rev. Lett. 41,1068.
[15] Budyko MI. 1969. The effffect of solar radiation variations on the climate of the Earth. Tellus 21, 611-619.
[16] Charbonneau, P. Corwin, EI. Parisi, G. Zamponi, F. 2012. Universal Microstructure and Mechanical Stability of Jammed Packings Phys. Rev. Lett. 109, 205501.
[17] Charbonneau, P. Kurchan, J. Parisi, G. Urbani, P. Zamponi, F. 2017. Glass and Jamming Transitions:
From Exact Results to Finite Dimensional Descriptions. Annu. Rev. Cond. Matt. Phys. 8, 265.
[18] Charney JG, Fj¨ortoft R, von Neumann J. 1950. Numer?ical Integration of the Barotropic Vorticity Equation. Tellus 2 (4), 237-254.
[19] Charney JG, Arakawa A, Baker DJ, Bolin B, Dickenson RE, Goody RM, Leith CE, Stommel HM, Wunsch CI. Carbon Dioxide and Climate: A Scientifific Assessment.
[20] Culina, J. Kravtsov, S. and Monahan, A.H. 2011. Stochastic Parameterization Schemes for Use in Realistic Climate Models, J. Atmos. Sci. 68, 284.
[21] de Almeida JRL, Thouless DJ. 1978. Stability of the Sherrington-Kirkpatrick solution of a spin glass model, J. Phys. A 11, 983.
[22] Doering CR. 2016: Mathematical Foundations of Stochastic Processes. 2015 Program of Study: Stochastic Processes in Atmospheric and Oceanic Dynamics, J. S. Wettlaufer and O. B¨uuhler, Eds., Woods Hole Oceanographic Institution Tech. Rep. WHOI-2016-05, 140, doi:10.1575/1912/8601.
[23] Doering CR. 2020. Turning up the heat in turbulent thermal convection. Proc. Nat. Acad. Sci. U.S.A. 117, 9671-9673.
[24] Edwards SF, Anderson PW. 1975. Theory of spin glasses. J. Physics F: Metal Physics, 5, 965.
[25] EPICA community members. 2004. Eight glacial cycles from an Antarctic ice core. Nature, 429 623-628.
[26] Frankignoul C, Hasselmann K. 1977. Stochastic climate models, Part II. Application to sea-surface temperature anomalies and thermocline variability. Tellus 29, 289305.
[27] Gardiner, C. Stochastic Methods. Springer, Berlin Heidelberg, Germany, 4th edition, 2009.
[28] Ghil M. 1976. Climate Stability for a Sellers-Type Model. J. Atmos. Sci. 33, 3-20.
[29] Ghil M, Lucarini V. 2020. The Physics of Climate Variability and Climate Change. Rev. Mod. Phys. 92, 035002.
[30] Ghofraniha N, Viola I, Di Maria F, Barbarella G, Gigli G, Leuzzi L, Conti C. 2015. Experimentalevidence of replica symmetry breaking in random lasers. Nat. Commun. 6, 6058 (See also Corrigendum in regards to Fig. 4).
[31] Glantz MH, Katz RW, Nicholls N. 1991 Teleconnections linking worldwide climate anomalies. Vol. 535. Cambridge: Cambridge University Press. 535 pg.
[32] Gleick J. 1992. Genius: The Life and Science of Richard Feynman, pp. 489 (Open Road Integr. Media, New York.)
[33] Gomes, A., Raposo, E., Moura, A. et al. 2016. Observation of L´evy distribution and replica symmetry breaking in random lasers from a single set of measurements. Sci. Rep. 6, 27987.
[34] González, I.R.R., Raposo, E.P., Macêdo, A.M.S. etal. 2018. Coexistence of turbulence-like and glassy be?haviours in a photonic system. Sci. Rep. 8, 17046.
[35] Guckenheimer, J. and Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer, New York, NY, 1983. 462 pg.
[36] Halsey TC, Jensen MH, Kadanoffff LP, Procaccia I, Shraiman BI. 1986. Fractal measures and their singularities: the characterization of strange sets. Phys. Rev. A 33, 1141-51.
[37] Hammond, AP. Corwin, EI. 2020. Experimental observation of the marginal glass phase in a colloidal glass. Proc. Nat. Acad. Sci. USA 117, 5714-5718.
[38] Hansen J, Russell G, Rind D, Stone P, Lacis A, Lebedeffff S, Travis L. 1983. Effiffifficient three-dimensional global models for climate studies: Models I and II. Mon. Wea. Rev. 111, 609-662.
[39] Hamilton K. 2020. At the dawn of global climate modeling: the strange case of the Leith atmosphere model. Hist. Geo Space Sci. 11, 93103.
[40] Hasselmann K. 1966. Feynman diagrams and interaction rules of wave-wave scattering processes. Rev. Geophys. 4, 1-32.
[41] Hasselmann K. 1967. Non-linear interactions treated by the methods of theoretical physics (with application to the generation of waves by wind). Proc. R. Soc. A 299, 77-100.
[42] Hasselmann K. 1976. Stochastic climate models part I. Theory. Tellus 28(6), 473-485.
[43] Hasselmann K. 1979. On the Signal-to-Noise Problem in Atmospheric Response Studies. In: Meteorology of Tropical Oceans. Ed. by D.B. Shaw. London: Roy Meteorol Soc., pp. 251 259.
[44] Hasselmann K. 1993. Optimal Fingerprints for the Detection of Time-Dependent Climate Change. J. Climate 6, 1957-1971.
[45] Hasselmann K. 1997. Multi-Pattern Fingerprint Method for Detection and Attribution of Climate Change. Clim. Dyn. 13, 601-611.
[46] Hegerl G, Hasselmann K, Cubasch U, Mitchell JFB, Roeckner E, Voss R, Waszkewitz J. 1997. Multi-
fifingerprint detection and attribution analysis of green?house gas, greenhouse gas-plus-aerosol and solar forced climate change. Clim. Dyn. 13, 613-634.
[47] Hegerl G, North GR. 1997. Comparison of Statistically Optimal Approaches to Detecting Anthropogenic Climate Change. J. Clim 10, 1125.
[48] Hegerl G, Zwiers F, Tebaldi C. 2011. Patterns of change: whose fifingerprint is seen in global warming? Environ. Res. Lett. 6, 044025.
[49] Hegerl G, Zwiers F. 2011. Use of models in detection and attribution of climate change. WIREs Clim. Change 2 570-91.
[50] Hopfifield JJ. 1982. Neural networks and physical systems with emergent collective computational properties. Proc. Nat. Acad. Sci. USA 79, 2554-2558.
[51] Iyer KP, Scheel JD, Schumacher J, Sreenivasan KR. 2020. Classical 1/3 scaling of convection holds up to Ra =10^15 . Proc. Nat. Acad. Sci. USA 117, 7594-7598.
[52] Jung T, Miller MJ, Palmer TN, Towers P, Wedi N, Achuthavarier D, Marx L. 2012. High-resolution global climate simulations with the ECMWF model in Project Athena: Experimental design, model climate and sea?sonal forecast skill. J. Climate 25, 3155-3172.
[53] Kirkpatrick S, Gelatt CD, Vecchi MP. 1983. Optimization by Simulated Annealing. Science 220, 671-680.
[54] Kirschvink JL. 1992. Late Proterozoic low-latitude global glaciation: The snowball Earth, in The Proterozoic Biosphere, edited by J. W. Schopf and C. Klein, pp. 51-52, Cambridge Univ. Press, New York.
[55] Knutti R, Sedlacek J. 2013. Robustness and uncertain ties in the new CMIP5 climate model projections. Nature Climate Change 3, 369-373
[56] Lorenz, EN. 1963. Deterministic nonperiodic flflow. J. Atmos. Sci. 20, 130–41.
[57] Lorenz, EN. 1992. The slow manifold-What is it? J. Atmos. Sci. 49, 2449-2451.
[58] Lyubovtseva YS, Gvishiani AD, Soloviev AA, Samokhina OO, Krasnoperov RI. 2020. Sixtieth
anniversary of the International Geophysical Year (1957-2017) – contribution of the Soviet Union. Hist.
Geo Space Sci. 11, 157171.
[59] Majda AJ, Timofeyev I, and Vanden-Eijnden E. 2001. A mathematical framework for stochastic climate models. Commun. Pure Appl. Math. 54, 891-974.
[60] Manabe, S, M¨oller, F. 1961. On the radiative equilib?rium and heat balance of the atmosphere. Mon. Wea. Rev. 89, 503–32.
[61] Manabe, S, Strickler, RF. 1964. Thermal equilibrium of the atmosphere with a convective adjustment J. Atmos. Sci. 21, 361–85.
[62] Manabe, S, Wetherald, RT. 1967. Thermal equilibrium of the atmosphere with a given distribution of relative humidity. J. Atmos. Sci. 24, 241–259.
[63] Manabe, S, Wetherald, RT. 1975. The Effffects of Dou?bling the CO2 Concentration on the climate of a General Circulation Model. J. Atmos. Sci. 32, 3–15.
[64] Mandelbrot, BB. 1974. Intermittent turbulence in selfsimilar cascades: divergence of high moments and dimension of the carrier. J. Fluid Mech. 62, 331-58.
[65] Mann, ME, Steinman, BA, and Miller, SK. 2020. Absence of internal multidecadal and interdecadal oscillations in climate model simulations. Nat Commun 11, 1–9.
[66] Malkus, WVR. 2001. Borders of disorder. Stud. Appl. Math. 107, 325-336.
[67] Meneveau, C. Sreenivasan, KR. 1987. Simple multifractal cascade model for fully developed turbulence. Phys. Rev. Lett. 59, 1424-27.
[68] M´ezard M, Parisi G, Virasoro M. 1987. Spin glass theory and beyond: An Introduction to the Replica Method and Its Applications. World Scientifific, Singapore. 476 pg.
[69] M´ezard M, Parisi G, Sourlas N, Toulouse G, Virasoro M. 1984. Nature of the spin-glass phase. Phys. Rev. Lett. 52, 1156.
[70] M´ezard, M. Parisi, G. and Zecchina, R. 2002. Ana?lytic and Algorithmic Solution of Random Satisfifiability Problems. Science 297, 812.
[71] Mitchell JM Jr. 1966. Stochastic models of air-sea in?teraction and climatic flfluctuation. (Symp. on the Arctic Heat Budget and Atmospheric Circulation, Lake Arrowhead, Calif., 1966) Mem. RM-5233-NSF, The Rand Corp., Santa Monica.
[72] Moon W, Agarwal S, Wettlaufer JS. 2018. Intrinsic Pink-Noise Multidecadal Global Climate Dynamics Mode. Phys. Rev. Lett. 121, 108701.
[73] Moon W, Wettlaufer JS. 2019. Coupling functions in climate. Phil. Trans. R. Soc. A 377, 20190006.
[74] Moura, A., et al. 2017. Replica Symmetry Breaking in the Photonic Ferromagneticlike Spontaneous Mode?Locking Phase of a Multimode Nd:YAG Laser, Phys. Rev. Lett. 119, 163902.
[75] M¨oller, F. 1963. On the inflfluence of changes in the CO2 concentration in air on the radiation balance of the Earth’s surface and on the climate. J. Geophys. Res. 68, 3877–86.
[76] Munk WH. 1960. Smoothing and persistence. J. Meteor. 17, 92-93.
[77] Orszag SA. 1971. Galerkin approximations to flflows within slabs, spheres, and cylinders. Phys. Rev. Lett. 26, 1100-1103.
[78] North GR. 1975. Theory of energy-balance climate models. J. Atmos. Sci. 32, 2033-43.
[79] North GR. 1975. Analytical solution to a simple climate model with diffffusive heat transport. J. Atmos. Sci. 32 (11), 1301-07.
[80] Palmer TN. 2001. A nonlinear dynamical perspective on model error: a proposal for nonlocal stochastic-dynamic parametrization in weather and climate prediction models. Q.J.R. Meteorol. Soc. 127, 279-304.
[81] Palmer TN. 2017. The primacy of doubt: Evolution of numerical weather prediction from determinism to probability. J. Adv. Model. Earth Syst. 9(2), 730-734.
[82] Parisi G. 1979. Toward a Mean Field Theory for Spin Glasses. Phys. Lett. A 73, 203.
[83] Parisi G. 1979. Infifinite number of order parameters for spin-glasses Phys. Rev. Lett. 43, 1754.
[84] Parisi G. 1980. Magnetic properties of spin glasses in a new mean fifield theory. J. Phys. A: Math. Gen. 13, 1887.
[85] Parisi G. 1983. Order parameter for spin-glasses. Phys. Rev. Lett. 50, 1946.
[86] Parisi G. 1988. Statistical Field Theory. (Addison?Wesley, Redwood City, CA. pp. 352)
[87] Parisi G. 2005. Brownian motion Nature 433, 221.
[88] Parisi G, Frisch U. 1985. On the singularity structure of fully developed turbulence. In Turbulence and Predictability in Geophysical Fluid Dynamics, ed. M Ghil, R Benzi, G Parisi, pp. 84-87. Amsterdam: North?Holland.
[89] Parisi, G and Zamponi F. 2010. Mean-fifield theory of hard sphere glasses and jamming. Rev. Mod. Phys. 82 (1), 789.
[90] Pierangeli, D., Tavani, A., Di Mei, F. et al. 2017. Obser?vation of replica symmetry breaking in disordered non?linear wave propagation. Nat Commun 8, 1501.
[91] Pierrehumbert RT. 2011. Principles of Planetary Climate. Cambridge Univ. Press, Cambridge, pp. 684.
[92] Pomeau, Y. The long and winding road. 2016. Nature Phys. 12, 198-199.
[93] Rainone, C. Urbani, P. 2016. Following the evolution of glassy states under external perturbations: the full replica symmetry breaking solution. J. Stat. Mech. Th. & Exp. 053302.
[94] Rawlins F, Ballard SP, Bovis KJ, Clayton AM, Li D, Inverarity GW, Payne TJ. 2007. The Met Offiffiffice global four-dimensional variational data assimilation scheme. Q. J. Royal Meteorol. Soc. 133, 347-362.
[95] Rissone, P. Corwin, EI. Parisi, G. 2021. Long-Range Anomalous Decay of the Correlation in Jammed Packings. Phys. Rev. Lett. 127, 038001.
[96] Read N. 2014. Short-range Ising spin glasses: The metastate interpretation of replica symmetry breaking. Phys. Rev. E 90 032142.
[97] Saltzman B. 1962. Finite amplitude free convection as an initial value problem-I. J. Atmos. Sci. 19, 329-341.
[98] Santer, BD et al., 2019. Celebrating the anniversary of three key events in climate change science. Nature Clim. Change 9, 180182.
[99] Sarkar, A., Shivakiran Bhaktha, B.N.; Andreasen, J. 2020. Replica Symmetry Breaking in a Weakly Scattering Optoflfluidic Random Laser. Sci. Rep. 10, 2628.
[100] Schrag DP, Berner RA, Hoffffman PF, Halverson GP. 2002. On the initiation of a snowball Earth, Geochem. Geophys. Geosyst. 3(6), doi:10.1029/2001GC00219.
[101] Sellers WD. 1969. A Global Climatic Model Based on the Energy Balance of the Earth-Atmosphere System. J. Appl. Meteor. 8, 392-400.
[102] Sherrington, D. and Kirkpatrick, S. 1975. Solvable Model of a Spin-Glass. Phys. Rev. Lett. 35, 1792.
[103] Strogatz, S.H. Nonlinear Dynamics and Chaos. West?view Press, 2000. 512 pg.
[104] Sreenivasan, KR. Antonia, RA. 1997. The phenomenology of small scale turbulence. Annu. Rev. Fluid Mech. 29, 435-72.
[105] Temam R. Infifinite-Dimensional Dynamical Systems in Mechanics and Physics. Springer, New York, NY, 1997.
[106] Thouless DJ, Anderson PW, Palmer RG. 1977. Solution of ‘Solvable model of a spin glass’. Phil. Mag. A 35, 593.
[107] Thouless, DJ. 1988. Phys. Today 41 (12), 110.
[108] Tommasi, F., Ignesti, E., Lepri, S., Cavalieri, S. 2016. Robustness of replica symmetry breaking phenomenology in random laser. Sci. Rep. 6, 37113.
[109] Tyndall J. 1861. On the absorption and radiation of heat by gases and vapours, and on the physical connexion of radiation, absorption, and conduction. Philosophical Magazine Series 4 22,169-194; 273-285.
[110] Untersteiner N. 2009. International Geophysical Year, 1957-1958: Drifting Station Alpha Documen?
tary Film, National Snow and Ice Data Center, doi.org/10.7265/N5MK69TW or nsidc.org/data/g02184.
[111] Wettlaufer, JS. 2016. Editorial. Climate Science: An Invitation for Physicists. Phys. Rev. Lett. 116, 150002.
[112] Wiin-Nielsen A. 1991. The birth of numerical weather prediction. Tellus A 43 (4), 36-52.
[113] Wunsch, C. Modern Observational Physical Oceanography: Understanding the Global Ocean (Princeton University Press, Princeton, NJ, 2015).
[114] The founders of this fifield are all now deceased. In the 50’s Stommel and Veronis began collaborating at the IAS within the von Neumann and Charney project, but their ultimate approach was to understand detailed pro?cesses rather than to study forecasting. A GFD school began in 1959: “with the aim of introducing a then relatively new topic in mathematical physics, geophysical flfluid dynamics, to graduate students in physical sciences. It has been held each summer since and promotes an exchange of ideas among the many distinct fifields that share a common interest in the nonlinear dy?
namics of rotating, stratifified flfluids. These fifields include classical flfluid dynamics, physical oceanography, meteorology, astrophysics, planetary atmospheres, geological flfluid dynamics, hydromagnetics, and applied math?ematics.” (https://gfd.whoi.edu)
[115] It is worth emphasizing that before the availability of computing, progress in explaining observations or making predictions in all of the physical sciences, including climate science, was made using pencil and paper calculations. Computers changed this completely and in an era precisely during which both theory and numerical modeling in this fifield were developing. For this reason, a conceptual bifurcation occurred in which “numerical realism” and “simple” theory began to evolve separately and the generality of the latter was largely viewed as a handicap rather than a great benefifit, whereas numerical climate models are only specififically relevant to the system under study [111]. After roughly half a century the theory of climate is now demonstrating its realism as well as having touched many fifields in dynamical systems along the way. This is due to the fact that nonlinear systems create emergent phenomena whereas GCMs act in a variety of ways as a fifilters of high frequency processes.


（参考文献可上下滑动查看）


原文链接：

https://www.nobelprize.org/uploads/2021/10/sciback_fy_en_21.pdf



地球系统科学读书会


从加拿大极端热浪，到德国的洪灾，从澳大利亚的森林大火，到中国河南的特大暴雨，极端天气已经成为新常态。气候变化正以我们所能感知的态势发生着。2021年诺贝尔物理学奖的一半被授予气象学家真锅淑郎和气象学家克劳斯·哈塞尔曼，“以表彰对地球气候的物理建模、量化变化和可靠地预测全球变暖”，表达了对人类命运的关切，也展现出从复杂系统视角研究地球气候环境的必要性。


集智俱乐部将组织地球系统科学读书会，自2021年12月14日开始，持续2个月，重点探讨近年来系统科学、人工智能等学科为地球系统科学提供的创新研究方法，包括统计物理、复杂网络分析、图网络与深度学习等，共读前沿文献，激发科研灵感。欢迎从事相关研究、对相关领域有浓厚兴趣的探索者报名参与交流。




推荐阅读



点击“阅读原文”，了解地球系统科学读书会