陈关荣:探讨复杂网络的高阶拓扑及其应用

导语
网络科学有助于我们更好地理解当今高度互联世界的演变,高阶相互作用对网络系统的动力学研究产生了重大影响,打破了原始单一类型成对交互的网络拓扑分析的局限性,为复杂网络的交互分析提供了新的思路。本文整理了陈关荣教授在2021年复杂网络学术会议中的报告,介绍了复杂网络高阶拓扑的相关概念,如何利用高阶拓扑解决网络同步问题,并且概述了高阶拓扑在脑科学、生态学、社会科学等多领域的应用。
研究领域:网络科学,高阶相互作用,网络同步问题,脑科学,生态学,社会科学

陈关荣 | 讲者
高爽 | 整理
梁金 | 审校
邓一雪 | 编辑
一、复杂网络高阶拓扑概述
一、复杂网络高阶拓扑概述
度(Degree):节点的连边数;
距离(Distance):两节点之间最短路径连边数的总数;
路和(Path-sum):节点到其它节点距离的总和;
圈(Cycle):闭路径;
周长(Girth):经过某节点的最短圈长;
团(Clique):全连接的子图;团也称为单纯形或单形(Simplex),在接下来的分析过程中,以单纯形为边界的复合图形称为单纯复形。
洞(Cavity):不是团的最小无关圈。
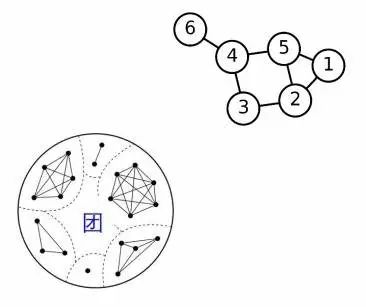
具体表示方法为:以“团”为基本单元,建立一系列二元域上的向量空间。其中:
· 以节点为基所得向量空间 C0,其维数是网络中的节点数目
· 以连边为基所得向量空间 C1,其维数是网络中的连线数目
· 以三角形为基的向量空间 C2,其维数是网络中三角形数目
 图2. 网络中各阶圈、团、洞、边界示意图
图2. 网络中各阶圈、团、洞、边界示意图 · 示性数:网络各阶团的数目分别记为 m0(节点数),m1(连线数),m2(三角形数),m3(四面体数)等等,则示性数公式为:![]()
· 贝蒂数(Betti):网络各边界矩阵的秩分别记为 r0=0(约定),r1(点线矩阵),r2(线面矩阵),r3(面体矩阵),等等。则贝蒂数公式为:![]()
二、高阶拓扑解决网络同步问题
二、高阶拓扑解决网络同步问题
· 全齐网络是同步最优网络
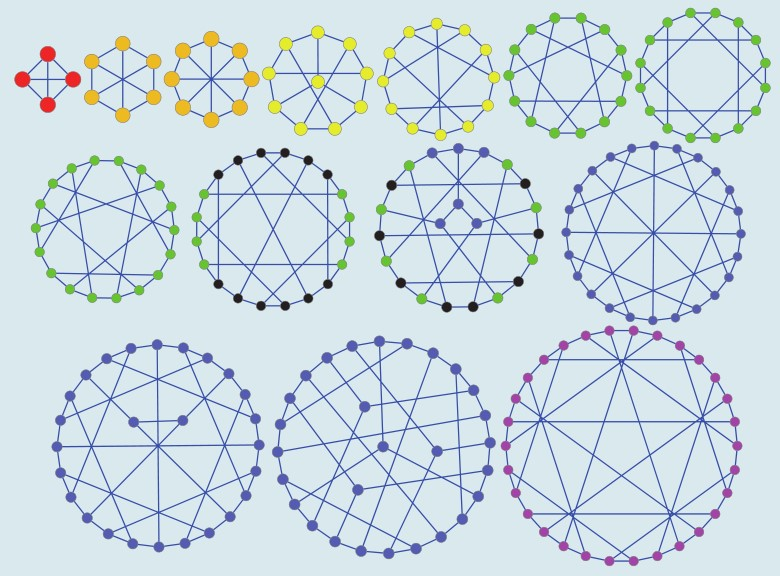
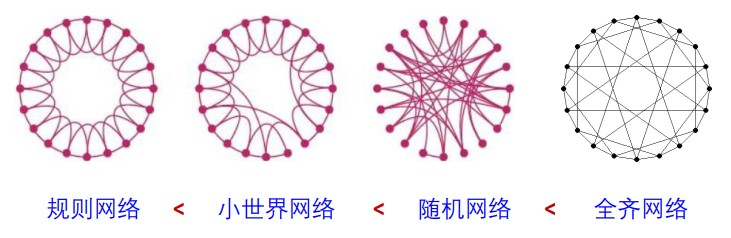
D.H. Shi, G. Chen, W.W.K. Thong, X.Y. Yan, Searching for optimal network topology with best possible synchronizability, IEEE Circ. Syst. Mag. 13(1): 66-75, 2013 https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=6468141
D. H. Shi, L. Y. Lyu, G. R. Chen, Totally homogeneous networks, National Science Review (2019) https://arxiv.org/ftp/arxiv/papers/1903/1903.11289.pdf
· 复杂网络中的高阶组织结构
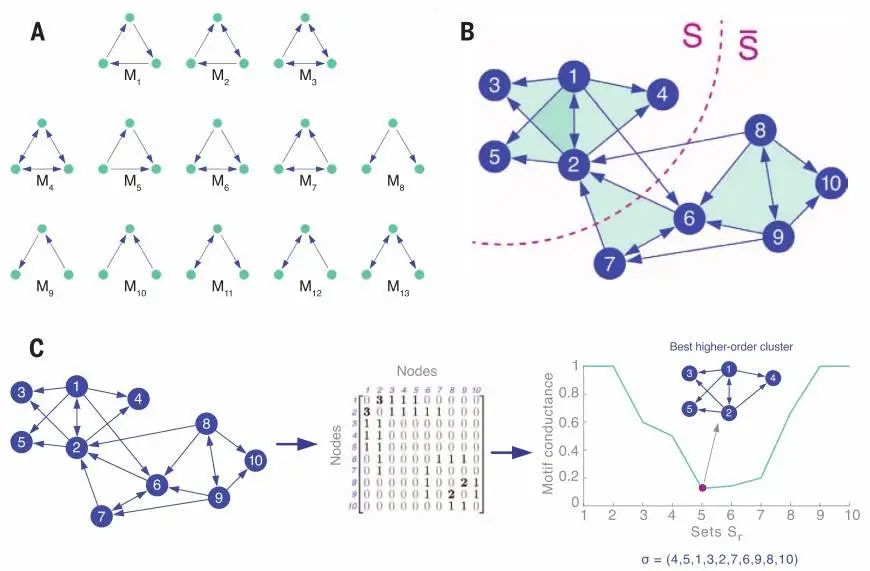
A.R. Benson, D.F. Gleich, J. Leskovec, Higher-order organization of complex networks, Science, 353: 163-166, 2016 https://www.science.org/doi/epdf/10.1126/science.aad9029

F. Battiston, G. Cencetti, I. Iacopini, V. Latora, M. Lucas, A. Patania, J.-G. Young, G. Petri, Networks beyond pairwise interactions: Structure and dynamics, Physics Reports, 847: 1-92, 2020 https://arxiv.org/abs/2006.01764v1
· 耦合高阶单纯复形上拓扑信号的同步
R. Ghorbanchian, J.G. Restrepo, J.J. Torres, G. Bianconi, Higher-order simplicial synchronization of coupled topological signals, Comm. Phys., 4: Paper 120, 2021 https://arxiv.org/abs/2011.00897v2
· 高维单纯复形上 Kuramoto 振子的相位同步

X. Dai, K. Kovalenko, M. Molodyk, Z. Wang, X. Li, D. Musatov, A.M. Raigorodskii, A. Bittner, G.D. Cooper, G. Bianconi, S. Boccaletti, D-dimensional oscillators in simplicial structures: Odd and even dimensions display different synchronization scenarios. Chaos, Solitons Fractals, 146: 110888, 2021 https://www.sciencedirect.com/science/article/pii/S0960077921002411
· 广义网络同步的高阶相互作用新形态
Y. Zhang, V. Latora, A.E. Motter, Unified treatment of synchronization patterns in generalized networks with higher-order, multilayer, and temporal interactions, Comm. Phys., 4: Article 195, 2021 https://arxiv.org/pdf/2010.00613v2.pdf
· 高阶网络同步的多阶拉普拉斯算子方法

M. Lucas, G. Cencetti, F. Battiston, Multiorder Laplacian for synchronization in higher-order networks, Phys. Rev. Research, 2: 033410, 2020 https://arxiv.org/pdf/2003.09734v3.pdf
· 单纯复形网络同步的稳定性
L.V. Gambuzza, F. Di Patti, L. Gallo, S.S. Lepri, M. Romance, R. Criado, M. Frasca, V. Latora, S. Boccaletti, Stability of synchronization in simplicial complexes, Nature Comm., 12: 1255, 2021 https://www.nature.com/articles/s41467-021-21486-9.pdf
三、高阶拓扑的多领域应用:
脑科学、生态学、社会科学
三、高阶拓扑的多领域应用:
脑科学、生态学、社会科学
1、脑科学
· 大脑功能网络的实证研究——团和洞的重要性
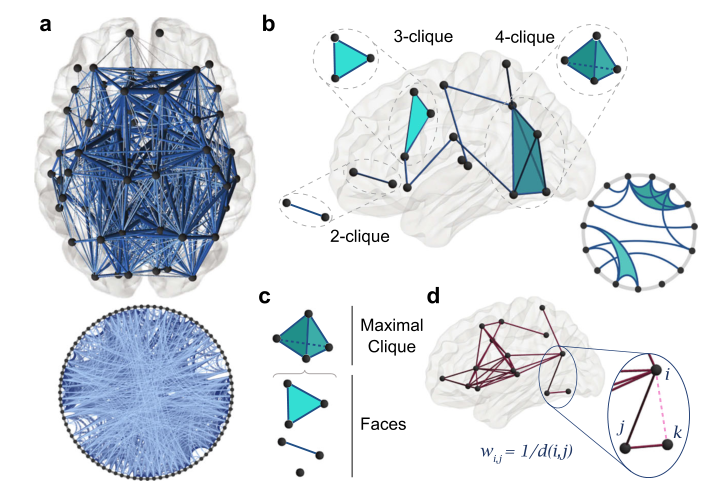
A.E. Sizemore, C. Giusti, A. Kahn, J.M. Vettel, R.F. Betzel, D.S. Bassett, Cliques and cavities in the human connectome. J. Comput. Neurosci. 44(1): 115-145, 2018 https://link.springer.com/content/pdf/10.1007/s10827-017-0672-6.pdf
束缚在空腔中的神经元 M.W. Reimann, M. Nolte, M. Scolamiero, K. Turner, R. Perin, G. Chindemi, P. Dłotko, R. Levi, K. Hess, H. Markram, Cliques of neurons bound into cavities provide a missing link between structure and function, Frontiers in Comput. Neurosci., 11: paper 48, 2017 https://www.frontiersin.org/articles/10.3389/fncom.2017.00048/full
2、生态学
· 物种的高阶相互作用决定生态系统的多样性
E. Bairey, E.D. Kelsic, R. Kishony, High-order species interactions shape ecosystem diversity, Nature Comm., 7: Article 12285, 2016 https://www.nature.com/articles/ncomms12285.pdf
· 生态系统中的高阶相互作用和群落稳定性
J. Grilli, G. Barabás, M.J. Michalska-Smith, S. Allesina, Higher-order interactions stabilize dynamics in competitive network models, Nature, 548: 210-213, 2017 https://www.nature.com/articles/nature23273.pdf
· 秀丽隐杆线虫的高阶神经网络结构与功能

S.J. Cook, et al., Whole-animal connectomes of both Caenorhabditis elegans sexes, Nature, 571: 63-71, 2019 https://www.nature.com/articles/s41586-019-1352-7.pdf
3、社会科学
· 社会网络中的高阶相互作用发展动力学

U. Alvarez-Rodriguez, F. Battiston, G.F. de Arruda, Y. Moreno, M. Perc, V. Latora, Evolutionary dynamics of higher-order interactions in social networks, Nature Human Behaviour, 5: 586-595, 2021 https://www.nature.com/articles/s41562-020-01024-1
4、其他新应用场景
· 计算拓扑学开始进入复杂网络研究领域——寻找高阶拓扑特征
B.J. Stolz, A.H. Heather, M.A. Porter, Persistent homology of time-dependent functional networks constructed from coupled time series. Chaos 27: 047410, 2017 https://arxiv.org/pdf/1605.00562.pdf E. Ibanez-Marcelo, L. Campioni, A. Phinyomark, G. Petri, E.L. Santarcangelo, Topology highlights mesoscopic functional equivalence between imagery and perception. NeuroImage 200: 437-449, 2019 https://www.researchgate.net/publication/344952631_Topology_highlights_mesoscopic_functional_equivalence_between_imagery_and_perception
· 识别超图中的高阶相互作用信息
F. Musciotto, F. Battiston, R.N. Mantegna, Detecting informative higher-order interactions in statistically validated hypergraphs, Comm. Phys., 4: Paper 218, 2021 https://www.nature.com/articles/s42005-021-00710-4.pdf
· 高阶相互作用改善网络群集行为的优化
P.S. Skardal, D. Taylor, L.A rola-Fernandez, A. Arenas, Higher-order interactions improve optimal collective dynamics on networks, arXiv 2021
· 高阶团网络与渗流过程
这篇文章研究了以团为基础的网络局部结构对网络渗流过程的影响。比较了带局部社团结构的随机图模型和带局部树状结构的随机图模型。发现了网络的平均度数越大,其局部树状结构对渗流过程的影响就越小。在高阶团网络上,与树状网络比较,渗流的不同行为几乎可以完全归因于度序列而不是社团结构的差异。
C. Stegehuis, T. Peron, Network processes on clique-networks with high average degree: the limited effect of higher-order structure, arXiv 2021 https://www.researchgate.net/publication/351279057_Network_processes_on_clique-networks_with_high_average_degree_the_limited_effect_of_higher-order_structure
· 复杂网络中的洞与鲁棒性
A.D. Zhou, S. Maletić, Y. Zhao, Robustness and percolation of holes in complex networks, Physica A, 502: 459-468, 2018 https://www.sciencedirect.com/science/article/pii/S0378437118302188
· 科学与技术知识网络中的高阶拓扑结构
T. Gebhart, R.J. Funk, The emergence of higher-order structure in scientific and technological knowledge networks, arXiv 2020 https://arxiv.org/pdf/2009.13620v1.pdf
· 最优高阶网络模型及其数据分析应用
R. Lambiotte, M. Rosvall, I. Scholtes, From networks to optimal higher-order models of complex systems, Nature Physics, 15: 313–320, 2019 https://www.nature.com/articles/s41567-019-0459-y.pdf
· 复杂系统高阶相互作用的物理学原理
F. Battiston et al., The physics of higher-order interactions in complex systems, Nature Physics, 17: 1093–1098, 2021 https://www.nature.com/articles/s41567-021-01371-4.pdf
· 计算复杂网络中的高阶团和洞
D.H. Shi*, Z.F. Chen, X. Sun, Q.H. Chen, C. Ma, Y. Lou, G.R. Chen*, Computing cliques and cavities in networks, Comm. Phys., accepted, 2021 https://arxiv.org/vc/arxiv/papers/2101/2101.00536v1.pdf
四、总结展望
四、总结展望
· 高阶结构的度量
· 高阶结构的生成模型
· 数据推断
参考文献
(参考文献可上下滑动查看)
网络科学集智课堂第三期报名中
从数学建模到多学科应用
网络科学集智课堂第三期报名中
从数学建模到多学科应用
推荐阅读
-
Nature Phycics:复杂网络中高阶相互作用的物理学 -
从经验到理论、从数据到网络——脑科学研究的四次范式转移 -
Science:大脑神经元复杂网络连接的新机制 -
《张江·复杂科学前沿27讲》完整上线! -
加入集智,一起复杂!
点击“阅读原文”,报名课程










