从古至今,人类孜孜不倦地试图规划和控制城市的发展,但研究表明城市往往是以自下而上的方式发展的,从而形成了以标度律为特征的城市分形现象。虽然城市标度律以及渗流模型成功地预测了城市的规模和分形结构,但城市发展背后的微观机制在很大程度上仍是未知。12月9日,清华大学电子工程系李勇团队在 Nature Computational Science 杂志上最新发表的一项研究,基于大规模城市模拟仿真平台首次揭示了城市宏观演化发展规律从人类微观移动行为中涌现的内在机理,表明人类移动中的社会交互机制和移动记忆机制是控制城市发展的两个基本规律。该成果极大拓宽了传统建模城市演化规律的统计物理模型,首次建立了连接个体移动行为与城市演化规律的理论桥梁,使得在城市规划与治理中考虑与微观城市居民行为的相互作用成为可能,对未来实现科学、灵活、精准的城市治理具有重要意义。
研究领域:行为建模,模拟仿真,城市演化规律,标度律,齐夫定律
论文题目:
Emergence of urban growth patterns from human mobility behavior
论文地址:
https://www.nature.com/articles/s43588-021-00160-6
城市是人类和资源在时空上的聚集,其为大规模社会协作和基础设施的复用提供了便利条件,能显著地提升社会经济效益。长时间尺度下城市发展存在显著的分形(Fractal)现象与三大发展规律[1,2]:城市面积分布的齐夫定律(Zipf’s Law),城市面积与城市人口间的超线性关系,以及城市人口的负指数空间分布。这些宏观规律的微观机理与演化模型是物理学、信息学、行为学等学科共同关注的“城市科学”交叉领域十几年来一直未能突破的重要科学问题。
通过变革“模型驱动”和“模拟仿真”的传统研究范式,这篇文章创新地提出了能同时建模社会交互机制和移动记忆机制的城市环境人类移动行为模型,并基于该移动模型建立了多智能体城市演化模型,通过理论分析和高效率城市模拟仿真技术表明该模型能准确预测城市演化中的分形现象和三大发展规律,为关联宏观层面的城市演化和微观层面的个体移动行为提供了一个理论桥梁。
理解城市复杂的发展,关键需要在微观动力学过程和宏观特征之间建立联系[3]。尽管以标度律(urban scaling laws)为主的宏观规律成功模拟了城市规模,但无法解释其中的微观动力机制。DLA (Diffusion-Limited Agglomeration)模型[4]和关联渗流 (correlated percolation) 模型 [5]将城市增长作为微观粒子的随机过程,成功解释了城市的分形特征,但植根于这些过程的人类微观行为机制仍旧是未知的。因此,需要开发一个基于人类行为的城市演化模型,用以链接微观机制和宏观城市发展,而人类移动行为[6,7]成为这项研究关注的焦点。
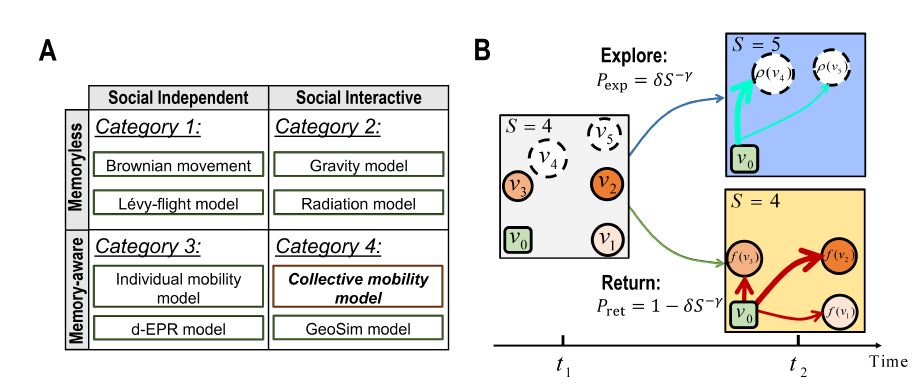
文章作者认为现有的人类移动模型可根据社会交互和移动记忆两个机制分为4类(图1A)。具体而言,如果一个人的运动会影响其他人,则人类运动模型被视为社会交互模型。此外,如果个人的未来移动行为受其历史移动的影响,则认为人类移动模型是具有记忆性的。第一类是移动概率呈正态分布的物理粒子随机运动模型,如布朗运动和列维飞行(Lévy flight)模型。第二类是起源于迁移研究的引力模型和辐射模型,两地的流动取决于它们的人口。这一机制解释了植根于社会互动背景下移动吸引力大小的问题,是社会交互机制[8]的体现。
第三类模型捕捉到了人类重复访问的个体移动模型 (IMM),个体前往某地与其历史访问频率成比例,但这一类模型只解释了个体日常的独立运动,不能捕捉个体间动态的相互作用。第四类的GeoSim模型将具有记忆性的个体移动模型和社交网络结合,整合了以上两个机制。但是社交网络是根据经验数据是输入预先设定的,不会随时间演变,因此该模型无法在大的时间尺度上跟踪城市发展。
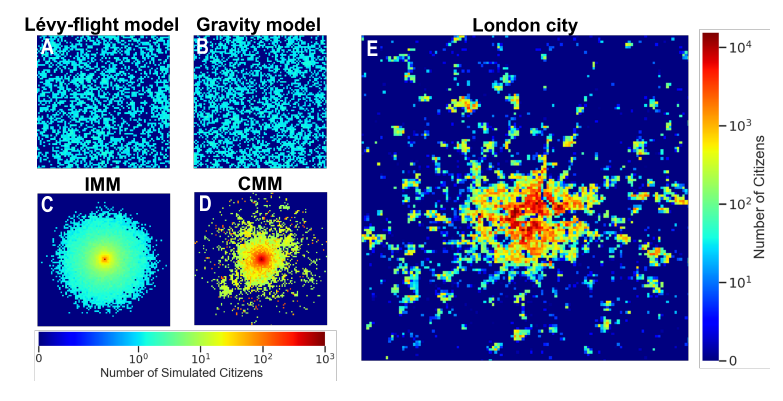
图1. 人类移动模型划分和集体移动模型(CMM)。子图B中的地点颜色越深表示之前访问过的频率越高,白色则表示一个没有访问过的新地点。
基于以上讨论,作者构建了集体移动模型 (CMM),旨在整合长期记忆效用和动态动态互动两个微观机制,用以预测城市的长期演变。集体移动模型(图1B)认为个体的移动遵循一个类似于个体移动模型的回访-探索过程,个体选择特定访问地点的概率与其之前的访问频率成正比。个人决定回访的概率可以计算为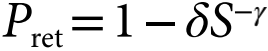 。其中S为先前访问地点的数量,δ控制初始回访的概率,γ控制回访概率如何随着访问地点S变化而变化。此外还有互补的概率表示个体探索新地点的概率
。其中S为先前访问地点的数量,δ控制初始回访的概率,γ控制回访概率如何随着访问地点S变化而变化。此外还有互补的概率表示个体探索新地点的概率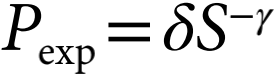 ,满足引力模型(式1),个体会根据距离和人口选择访问一个新地点。其中人口
,满足引力模型(式1),个体会根据距离和人口选择访问一个新地点。其中人口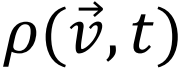 是基于t时刻所有个体的位置瞬间计算的,耦合常数
是基于t时刻所有个体的位置瞬间计算的,耦合常数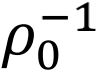 可被视为控制人口吸引力强度的平滑参数,即增加
可被视为控制人口吸引力强度的平滑参数,即增加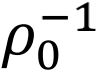 将减少探索新地点的概率,从而增加社会互动的强度。
将减少探索新地点的概率,从而增加社会互动的强度。
受关联渗流模型强空间相关性的启发,作者关注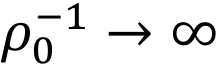 时个体强交互极限的移动,特别的
时个体强交互极限的移动,特别的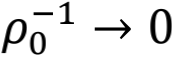 时个体相互独立,因此个体移动模型是集体移动模型没有个体交互状态下的一个特例。由此,文章提出的集体移动模型能够以自组织的方式模拟城市在任意时间尺度上的增长,而不依赖于任何外部输入。
其中P是二维空间(d=2)地点
时个体相互独立,因此个体移动模型是集体移动模型没有个体交互状态下的一个特例。由此,文章提出的集体移动模型能够以自组织的方式模拟城市在任意时间尺度上的增长,而不依赖于任何外部输入。
其中P是二维空间(d=2)地点 到
到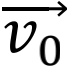 移动的概率,ρ0是(逆)耦合常数,
移动的概率,ρ0是(逆)耦合常数,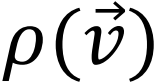 为地点
为地点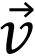 的人口密度。
的人口密度。
图2. 四种不同的人类移动模型仿真的人口分以及真实城市人口分布。
为了证明模型的预测力,作者通过构建多智能体城市演化模型(详见原文),将上述四类人类移动模型用于预测城市人口分布的演化。将模拟的城市系统的形态与经验观测结果进行比较,结果显示(图2),集体移动模型成功地再现了城市系统中紧凑的城市中心,市中心周边呈现出显著的分形几何,并且城市周围形成了许多子集群。而现实世界的几何形状则受到地理特征的影响,例如湖泊和河流,伦敦城市仍然表现出密集的城市中心和分形周界的突出特征。与之相比,列维飞行模型和引力模型模拟的城市人口呈均匀分布,而个体移动模型预测人口在市中心周边均匀增长。以上说明了集体移动模型具有较高的再现城市形态和预测未来是否会发展到特定位置的准确性。
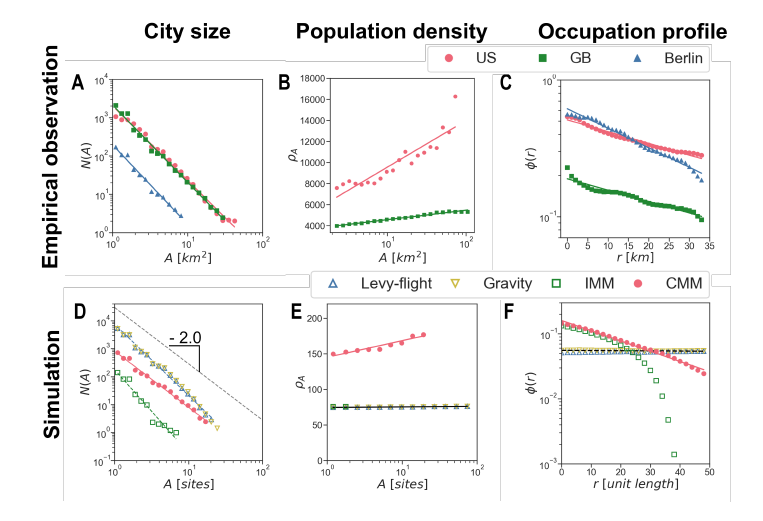
为了进一步检验集体移动模型在再现城市发展模式方面的能力,作者利用该模型对三大经验法则在不同国家的城市中(美、英、德)进行了验证,即城市面积分布的齐夫定律,城市面积与城市人口间的超线性关系,以及城市人口的负指数空间分布。
齐夫定律表征了的城市数量随其面积增加而减少的规模标度律,实证分析显示(图3A)不同国家城市的幂律指数在1.94-2.08之间,而在四类不同人类移动模型仿真中只有集体移动模型预测的幂律指数范围在上述实证区间内(2.02),其他模型均偏差较大(图3D)。
图3B显示,在不同国家城市中都广泛观测到人口随城市规模异速增长的超线性关系。最近的研究表明,城市地区人口集中的成本和收益之间的平衡可以解释这种超线性增长现象。这个解释包含两个假设: 从激烈的社会互动中获得的平均收益与人口密度成正比;平均生活成本正比于探索城市的典型旅行距离。图3E对比了四种模型的仿真结果,发现所提出的集体移动模型精确地再现了超线性关系,相反其他三个模型仿真结果系数为0,无法识别城市面积和人口之间的关系。
图3C&F表明,列维飞行模型和引力模型均无法预测城市人口密度的负指数空间分布,而由于社会互动的缺乏,个体移动模型无法在城市边缘区域产生大的子集群,导致城市边缘区域的职业密度急剧下降。与此相反,集体移动模型很好地预测了城市人口的密度分布。此外,随着越来越多的人口从市中心向周边地区转移,基于社会互动机制,周边地区对外来流动的吸引力将增强, 而长期记忆机制会在城市中心保持一个密集的区域。因此,社会互动和长期记忆机制的结合会导致城市周边轮廓逐渐变平,这说明集体移动模型能够以自组织的方式模拟周边区域吸引力逐渐增加的情况。
图3. 美国、英国和德国柏林城市增长模式的实证比较以及不同人类移动模型模拟的城市增长模式
A是城市面积的大小和N(A)是城市的数量,ρA为人口密度,r为距市中心距离,Φ(r)为人口密度
在多智能体仿真建模中,有三个重要的参数可能会影响城市系统的模拟:α、ρ0和平均人口密度ω。α是表征出行距离成本的主要参数,控制着出行的距离分布。在模拟中,根据经验观察将其设为0.55。ρ0主要控制着社会交互的机制,决定了个体探索更多人口区域的可能性,在之前的模拟中设置为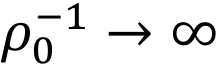 ,以重现强交互的城市系统。平均人口密度ω定义为人口数量与地点数量之比,即 ω= M/l2,代表了个体在每个单位空间中会遇到的社交互动的数量。作者进一步分析了这三个参数如何影响集体移动模型的特性。
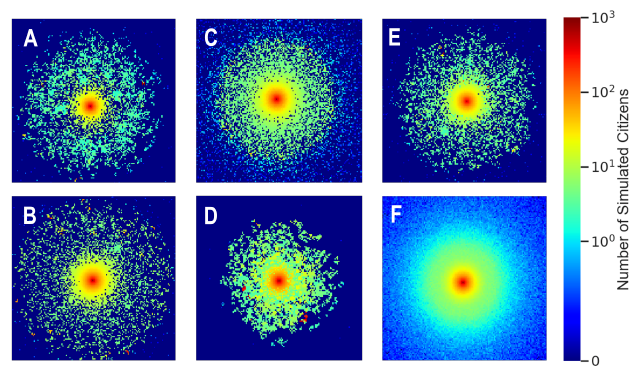
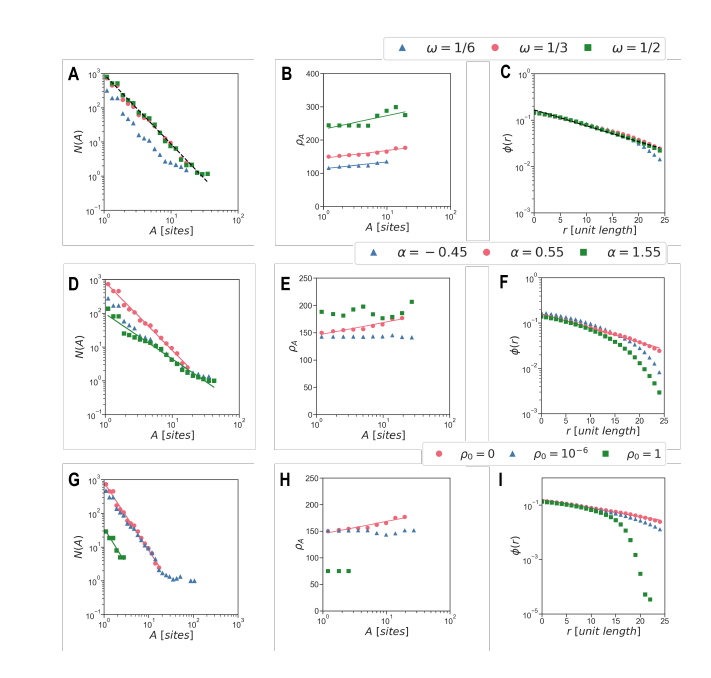
首先,如图4A&B所示,ω参数对城市系统的分形形态没有显著影响,并且图5A-C也表明城市规模分布、人口增长模式和城市人口密度分布均与不同ω设置下的经验观察结果一致。这些结果表明,不同人口密度的城市增长模式是稳健的。
,以重现强交互的城市系统。平均人口密度ω定义为人口数量与地点数量之比,即 ω= M/l2,代表了个体在每个单位空间中会遇到的社交互动的数量。作者进一步分析了这三个参数如何影响集体移动模型的特性。
首先,如图4A&B所示,ω参数对城市系统的分形形态没有显著影响,并且图5A-C也表明城市规模分布、人口增长模式和城市人口密度分布均与不同ω设置下的经验观察结果一致。这些结果表明,不同人口密度的城市增长模式是稳健的。
图4.不同参数设置下集体移动模型的模拟结果比较。每次模拟中改变一个参数的值:(A)ω=1/6,(B)ω=1/2,(C)α= −0.45,(D) α=1.55,(E)ρ0=10-6 ,(F)ρ0=1
其次,α参数对模拟城市系统的紧凑性有显著影响,如图4C&D所示,当α小于经验值时,城市系统的占用区域更加分散;当大于经验值时,模拟城市系统更具凝聚力,并产生更大的子集群。同时,图5D-F显示,当与经验值不同时,城市规模分布、人口增长模式和城市人口密度分布都偏离了经验规则。这表明,它不仅是人类移动行为的一个重要参数,而且从根本上控制着城市的增长。
最后,图4E&F显示,当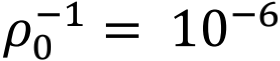 时,与
时,与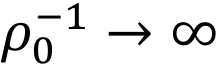 的情况相似,城市系统表现出显著的分形形态,但ρ0=1时分形形态消失,并在城市周边呈现同质增长。图5H&I也表明,ρ0=1时人口增长模式和城市人口密度分布偏离了经验规则,说明集体移动模型能够再现一个强互动的城市演化体系,而假设个体独立的个体移动模型只是它的一个特例。
的情况相似,城市系统表现出显著的分形形态,但ρ0=1时分形形态消失,并在城市周边呈现同质增长。图5H&I也表明,ρ0=1时人口增长模式和城市人口密度分布偏离了经验规则,说明集体移动模型能够再现一个强互动的城市演化体系,而假设个体独立的个体移动模型只是它的一个特例。
图5. 不同参数设置下再现城市增长模式的比较。每个面板中改变一个参数值。
这一研究成果首次揭示了城市复杂系统宏观演化发展规律的微观移动行为机理,捕捉到了这一复杂自组织本质,兼具宏观预测能力和微观可解释性,使得在大数据和人工智能时代,通过利用微观数据建模能力和智能技术支撑的模拟仿真技术,在城市政策制定中既能充分评估城市未来的演化态势又能综合考虑与微观个体行为的相互作用,能有效支撑科学、灵活、精准的城市治理。
此外,集体移动模型不仅能为城市规划、资源配置和交通治理等实践领域提供理论参考,有效支撑数据和智能时代的智慧城市应用;还为将来基于该模型在不同领域的通用性开发和适配以及基于多元大数据的实证分析提供了重要参考。
1.Batty, M. (2008). The size, scale, and shape of cities. science, 319(5864), 769-771.
2.Bettencourt, L. M. (2013). The origins of scaling in cities. science, 340(6139), 1438-1441.
3.Dong, L., Huang, Z., Zhang, J., & Liu, Y. (2020). Understanding the mesoscopic scaling patterns within cities. Scientific reports, 10(1), 1-11.
4.Makse, H. A., Havlin, S., & Stanley, H. E. (1995). Modelling urban growth patterns. Nature, 377(6550), 608-612.
5.Makse, H. A., Andrade, J. S., Batty, M., Havlin, S., & Stanley, H. E. (1998). Modeling urban growth patterns with correlated percolation. Physical Review E, 58(6), 7054.
6.Gonzalez, M. C., Hidalgo, C. A., & Barabasi, A. L. (2008). Understanding individual human mobility patterns. nature, 453(7196), 779-782.
7.Brockmann, D., Hufnagel, L., & Geisel, T. (2006). The scaling laws of human travel. Nature, 439(7075), 462-465.
8.Simini, F., González, M. C., Maritan, A., & Barabási, A. L. (2012). A universal model for mobility and migration patterns. Nature, 484(7392), 96-100.
集智斑图顶刊论文速递栏目上线以来,持续收录来自Nature、Science等顶刊的最新论文,追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能,每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅:

点击“阅读原文”,追踪复杂科学顶刊论文


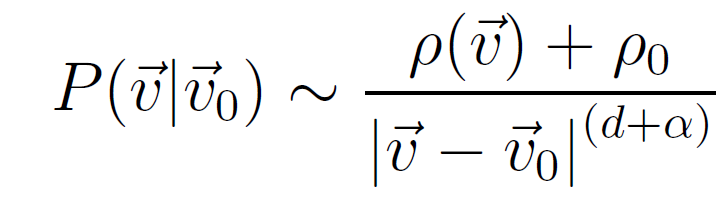
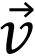 到
到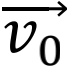 移动的概率,ρ0是(逆)耦合常数,
移动的概率,ρ0是(逆)耦合常数,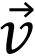 的人口密度。
的人口密度。