-
Anderson, P.W.: More if different: Broken Symmetry and the nature of hierarchical structure in sci- ence. Science 177, 393–396 (1972)
-
Laughlin, R.B., Pines, D., Schmalian, J., Stojkovic, B.P., Wolynes, P.: The middle way. Proc. Natl. Acad. Sci. USA 97, 32–37 (2000)
-
Qian, H., Ao, P., Tu, Y.H., Wang, J.: A framework towards understanding mesoscopic phenomena: emesrgent unpredictability, symmetry breaking and dynamics across scales. Chem. Phys. Lett. 665, 153–161 (2016)
-
Hopfield, J.J.: Physics, computation, and why biology looks so different. J. Theor. Biol. 171, 53–60 (1994)
-
Fang, X., Kruse, K., Lu, T., Wang, J.: Nonequilibrium physics in biology. Rev. Mod. Phys. 91, 045004 (2019)
-
Wang, J.: Landscape and flux theory of non-equilibrium dynamical systems with application to biol- ogy. Adv. Phys. 64, 1–137 (2015)
-
Frauenfelder, H., Parak, F., Young, R.D.: Conformational substates in proteins. Annu. Rev. Biophys Biophy. Chem. 17, 451 (1988)
-
Frauenfelder, H., Sligar, S., Wolynes, P.: The energy landscapes and motions of proteins. Science 254, 1598–1603 (1991)
-
Frauenfelder, H., Wolynes, P.G.: Biomolecules: where the physics of complexity and simplicity meet. Phys. Today. 47, 58–64 (1994)
-
Austin, R.H., Beeson, K.W., Eisenstein, L., Frauenfelder, H., Gunsalus, I.C.: Dynamics of ligand binding to myoglobin. Biochemistry 14, 5355–5373 (1975)
-
Chu, X., Wang, J.: Specificity and affinity quantification of flexible recognition from underlying energy landscape topography. PLOS Comp. Biol. 10, e1003782 (2014)
-
Chu, X., Wang, J.: Microscopic chromosomal structural and dynamical origin of cell differentiation and reprogramming. Adv. Sci. 7, 2001572 (2020)
-
Frauenfelder, H., Petsko, G.A., Tsernoglou, D.: Temperature-dependent X-ray diffraction as a probe of protein structural dynamics. Nature 280, 558–563 (1979)
-
Levinthal, C.: Mossbauer Spectroscopy in Biological Systems: Proceedings of a Meeting Held at Allerton House, Monticello, Illinois. Debrunner P., Tsibris J., Munck E, Proceedings of a meeting held at Allerton House, pp. 22–24 (1969)
-
Wang, J., Verkhivker, G.M.: Energy landscape theory, funnels, specificity, and optimal criterion of biomolecular binding. Phys. Rev. Lett. 90, 188101 (2003)
-
Bryngelson, J.D., Onuchic, J.N., Socci, N.D., Wolynes, P.G.: Funnels, pathways, and the energy land- scape of protein folding: a synthesis. Proteins Struct. Funct. Bioinform. 21, 167–195 (1995)
-
Onuchic, J.N., Luthey-Schulten, Z., Wolynes, P.G.: Theory of protein folding: the energy landscape perspective. Annu. Rev. Phys. Chem. 48, 545–600 (1997)
-
Dill, K.A., Chan, H.S.: From Levinthal to pathways to funnels. Nat. Struct. Biol. 4, 10–19 (1997)
-
Wang, J., Oliveira, R.J., Chu, X.K., Whitford, P.C., Chahine, J., Han, W., Wang, E.K., Onuchic, J.N., Leite, V.B.P.: Topography of funneled landscapes determines the thermodynamics and kinetics of protein folding. Proc. Natl. Acad. Sci. USA 109, 15763–15768 (2012)
-
Chu, X.K., Gan, L.F., Wang, E.K., Wang, J.: Quantifying the topography of the intrinsic energy land- scape of flexible biomolecular recognition. Proc. Natl. Acad. Sci. USA 110, E2342–E2351 (2013)
-
Wang, J., Zheng, X., Yang, Y., Drueckhammer, D., Wei, Y., Verkhivker, G., Wang, E.: Quantifying intrinsic specificity: a potential complement to affinity in drug screening. Phys. Rev. Lett. 99, 198101 (2007)
-
Yan, Z., Zheng, X., Wang, E., Wang, J.: Thermodynamic and kinetic specificities of ligand binding. Chem. Sci. 4, 2387–2395 (2013)
-
Zheng, X.L., Liu, Z.J., Li, D., Wang, E.K., Wang, J.: Rational drug design: the search for ras protein hydrolysis intermediate conformation inhibitors with both affinity and specificity. Curr. Pharm. Des. 19, 2246–2258 (2013)
-
Yan, Z.Q., Wang, J.: Quantifying the kinetic residence time as a potential complement to affinity for the aptamer selection. J. Phys. Chem. B 122, 8380–8385 (2018)
-
Yan, Z., Wang, J.: Incorporating specificity into optimization: evaluation of SPA using CSAR 2014 and CASF 2013 benchmarks. J. Comput. Aid. Mol. Des. 30, 219–227 (2016)
-
Yan, Z., Wang, J.: Specificity quantification of biomolecular recognition and its implication for drug discovery. Sci. Rep. 2, 309 (2012)
-
Zheng, X.L., Gan, L.F., Wang, E.K., Wang, J.: Pocket-based drug design: exploring pocket space. Aaps J. 15, 228–241 (2013)
-
Zheng, X.L., Wang, J.: The universal statistical distributions of the affinity, equilibrium constants, kinetics and specificity in biomolecular recognition. PLOS Comput. Biol. 11, 24 (2015)
-
Zheng, X.L., Wang, J.: Universal statistical fluctuations in thermodynamics and kinetics of single molecular recognition. Phys. Chem. Chem. Phys. 18, 8570–8578 (2016)
-
Yan, Z., Guo, L., Hu, L., Wang, J.: Specificity and affinity quantification of protein-protein interac- tions. Bioinformatics 29, 1127–1133 (2013)
-
Yan, Z., Wang, J.: Optimizing scoring function of protein-nucleic acid interactions with both affinity and specificity. PLoS ONE 8, e74443 (2012)
-
Yan, Z., Wang, J.: Optimizing the affinity and specificity of ligand binding with the inclusion of sol- vation effect. Proteins Struct. Funct. Bioinform. 83, 1632–1642 (2015)
-
Yang, Y.L., Li, G.H., Zhao, D.Y., Yu, H.Y., Zheng, X.L., Peng, X.D., Zhang, X., Fu, T., Hu, X.Q., Niu, M.S., Ji, X.F., Zou, L.B., Wang, J.: Computational discovery and experimental verification of tyrosine kinase inhibitor pazopanib for the reversal of memory and cognitive deficits in rat model neurodegeneration. Chem. Sci. 6, 2812–2821 (2015)
-
Zhao, W.J., Li, D., Liu, Z.J., Zheng, X.L., Wang, J., Wang, E.K.: Spiclomazine induces apoptosis associated with the suppression of cell viability, migration and invasion in pancreatic carcinoma cells. PLoS ONE 8, 10 (2013)
-
Liu, Z., Li, D., Zhao, W., Zheng, X., Wang, E.: A potent lead induces apoptosis in pancreatic cancer cells. PLoS ONE 7, e37841 (2012)
-
Liu, Z., Zheng, X., Yang, X., Wang, E., Wang, J.: Affinity and specificity of levamlodipine-human serum albumin interactions: insights into its carrier function. Biophys. J. 96, 3917–3925 (2009)
-
Liu, Z.J., Li, D., Zheng, X.L., Wang, E.K., Wang, J.: Selective induction of apoptosis: promising therapy in pancreatic cancer. Curr. Pharm. Des. 19, 2259–2268 (2013)
-
Liu, Z.J., Zheng, X.L., Wang, J., Wang, E.K.: Molecular analysis of thymopentin binding to HLA-DR molecules. PLoS ONE 2, 8 (2007)
-
Li, D., Liu, Z.J., Zhao, W.J., Zheng, X.L., Wang, J., Wang, E.K.: A small-molecule induces apoptosis and suppresses metastasis in pancreatic cancer cells. Eur. J. Pharm. Sci. 48, 658–667 (2013)
-
Liu, F., Chu, X., Lu, H.P., Wang, J.: Molecular mechanism of multispecific recognition of Calmodulin through conformational changes. Proc. Natl. Acad. Sci. USA 114, E3927–E3934 (2017)
-
Liu, F., Qing, H., Wang, J.: Mechanochemical model of the power stroke of the single-headed motor protein KIF1A. J. Phys. Chem. B 122, 11002–11013 (2018)
-
Wang, Y., Chu, X.K., Longhi, S., Roche, P., Han, W., Wang, E.K., Wang, J.: Multiscaled exploration of coupled folding and binding of an intrinsically disordered molecular recognition element in mea- sles virus nucleoprotein. Proc. Natl. Acad. Sci. USA 110, E3743–E3752 (2013)
-
Wang, Y., Chu, X.K., Suo, Z.C., Wang, E.K., Wang, J.: Multidomain protein solves the folding prob- lem by multifunnel combined landscape: theoretical investigation of a Y-family DNA polymerase. J. Am. Chem. Soc. 134, 13755–13764 (2012)
-
Chu, X., Liu, F., Maxwell, B.A., Wang, Y., Suo, Z., Wang, H., Han, W., Wang, J.: Dynamic confor- mational change regulates the protein-DNA recognition: an investigation on binding of a Y-family polymerase to its target DNA. PLoS Comput. Biol. 10, e1003804 (2014)
-
Yan, Z., Wang, J.: Funneled energy landscape unifies principles of protein binding and evolution. Proc. Natl. Acad. Sci. USA 117, 27218–27223 (2020)
-
Yan, Z., Wang, J.: Superfunneled energy landscape of protein evolution unifies the principles of pro- tein evolution, folding, and design. Phys. Rev. Lett. 122, 018103 (2019)
-
Yan, Z., Wang, J.: SPA-LN: a scoring function of ligand–nucleic acid interactions via optimizing both specificity and affinity. Nucleic Acids Res. 45, e110 (2017)
-
Kar, G., Keskin, O., Gursoy, A., Nussinov, R.: Allostery and population shift in drug discovery. Curr. Opin. Pharmacol. 10, 715–722 (2010)
-
Dunker, A.K., Lawson, J.D., Brown, C.J., Williams, R.M., Romero, P., Oh, J.S., Oldfield, C.J., Campen, A.M., Ratliff, C.M., Hipps, K.W.: Intrinsically disordered protein. J. Mol. Graph. Model. 19, 26–59 (2001)
-
Onuchic, J.N., Levy, Y., Wolynes, P.G.: Fly-casting in protein? DNA binding:? Frustration between protein folding and electrostatics facilitates target recognition. J. Am. Chem. Soc. 129, 738–739 (2007)
-
Levy, Y., Wolynes, P.G., Onuchic, J.N.: Protein topology determines binding mechanism. Proc. Natl. Acad. Sci. USA 101, 511–516 (2004)
-
Wang, J., Xu, L., Wang, E.: Optimal specificity and function for flexible biomolecular recognition. Biophys. J. 92, L109–L111 (2007)
-
Zhao, L.C., Lu, H.P., Wang, J.: Exploration of multistate conformational dynamics upon ligand bind- ing of a monomeric enzyme involved in pyrophosphoryl transfer. J. Phys. Chem. B 122, 1885–1897 (2018)
-
Zhao, L.C., Suarez, I.P., Gauto, D.F., Rasia, R.M., Wang, J.: The key role of electrostatic interactions in the induced folding in RNA recognition by DCL1-A. Phys. Chem. Chem. Phys. 20, 9376–9388 (2018)
-
Chu, X.K., Suo, Z.C., Wang, J.: Investigating the trade-off between folding and function in a multid- omain Y-family DNA polymerase. Elife 9, 40 (2020)
-
Chu, X.K., Suo, Z.C., Wang, J.: Confinement and crowding effects on folding of a multidomain Y-family DNA polymerase. J. Chem. Theory. Comput. 16, 1319–1332 (2020)
-
Chu, X.K., Wang, J.: Position-, disorder-, and salt-dependent diffusion in binding-coupled-folding of intrinsically disordered proteins. Phys. Chem. Chem. Phys. 21, 5634–5645 (2019)
-
Chu, X.K., Wang, Y., Gan, L.F., Bai, Y.W., Han, W., Wang, E.K., Wang, J.: Importance of electro- static interactions in the association of intrinsically disordered histone chaperone Chz1 and histone H2A.Z-H2B. PLOS Comput. Biol. 8, 11 (2012)
-
Chu, W.T., Chu, X., Wang, J.: Investigations of the underlying mechanisms of HIF-1α and CITED2 binding to TAZ1. Proc. Natl. Acad. Sci. USA 117, 201915333 (2020)
-
Chu, W.T., Chu, X.K., Wang, J.: Binding mechanism and dynamic conformational change of C subu- nit of PKA with different pathways. Proc. Natl. Acad. Sci. USA 114, E7959–E7968 (2017)
-
Chu, W.T., Clarke, J., Shammas, S.L., Wang, J.: Role of non-native electrostatic interactions in the coupled folding and binding of PUMA with Mcl-1. PLOS Comput. Biol. 13, 20 (2017)
-
Chu, W.T., Nesbitt, N.M., Gnatenko, D.V., Li, Z., Zhang, B., Seeliger, M.A., Browne, S., Mantle, T.J., Bahou, W.F., Wang, J.: Enzymatic activity and thermodynamic stability of biliverdin IXβ reductase are maintained by an active site serine. Chem. Eur. J. 23, 1891–1900 (2017)
-
Chu, W.T., Shammas, S.L., Wang, J.: Charge interactions modulate the encounter complex ensemble of two differently charged disordered protein partners of KIX. J. Chem. Theory. Comput. 16, 3856– 3868 (2020)
-
Chu, W.T., Suo, Z.C., Wang, J.: Binding-induced conformational changes involved in sliding clamp PCNA and DNA polymerase DPO4. Iscience 23, 24 (2020)
-
Chu, W.T., Wang, J.: Energy landscape topography reveals the underlying link between binding speci- ficity and activity of enzymes. Sci. Rep. 6, 9 (2016)
-
Chu, W.T., Wang, J.: Quantifying the intrinsic conformation energy landscape topography of proteins with large-scale open-closed transition. ACS Cent. Sci. 4, 1015–1022 (2018)
-
Chu, W.T., Wang, J.: Thermodynamic and sequential characteristics of phase separation and droplet formation for an intrinsically disordered region/protein ensemble. PLOS Comput. Biol. 17, 20 (2021)
-
Chu, W.T., Wang, J.: Influence of sequence length and charged residues on Swc5 binding with histone H2A–H2B. Proteins Struct. Funct. Bioinform. 89, 512–520 (2021)
-
Van Kampen, N.G.: Stochastic Processes in Physics and Chemistry, 3rd edn. Elsevier, Amsterdam (2007)
-
Reichl, L.E.: A Modern Course in Statistical Physics, 3rd Revised and Updated Edition. University of Texas Press, Texas (1984)
-
Swain, P.S., Elowitz, M.B., Siggia, E.D.: Intrinsic and extrinsic contributions to stochasticity in gene expression. Proc. Natl. Acad. Sci. USA 99, 12795–12795 (2002)
-
Hu, G.: Stochastic Force and Nonlinear Systems. Shanghai Science Education, Shanghai (1995)
-
Gillespie, D.T.: A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Computat. Phys. 22, 403–434 (1976)
-
Haken, H.: Advanced Synergetics: Instability Hierarchies of Self-Organizing Systems and Devices. Springer, Berlin (1983)
-
Wang, J., Xu, L., Wang, E.K.: Potential landscape and flux framework of nonequilibrium networks: Robustness, dissipation, and coherence of biochemical oscillations. Proc. Natl. Acad. Sci. USA 105, 12271–12276 (2008)
-
Xu, L., Wang, J.: Quantifying the potential and flux landscapes of multi-locus evolution. J. Theor. Biol. 422, 31–49 (2017)
-
Xu, L., Wang, J.: Landscape and flux for quantifying global stability and dynamics of game theory. PLoS ONE 13, e0201130 (2018)
-
Xu, L., Wang, J.: Curl flux as a dynamical origin of the bifurcations/phase transitions of nonequilib- rium systems: cell fate decision making. J. Phys. Chem. B 124, 2549–2559 (2020)
-
Xu, L., Zhang, F., Wang, E.K., Wang, J.: The potential and flux landscape, Lyapunov function and non-equilibrium thermodynamics for dynamic systems and networks with an application to signal- induced Ca2+ oscillation. Nonlinearity 26, R69–R84 (2013)
-
Xu, L., Zhang, F., Zhang, K., Wang, E.K., Wang, J.: The potential and flux landscape theory of ecol- ogy. PLoS ONE 9, e86746 (2014)
-
Xu, L., Zhang, K., Wang, J.: Exploring the mechanisms of differentiation, dedifferentiation, repro- gramming and transdifferentiation. PLoS ONE 9, e105216 (2014)
-
Zhang, F., Xu, L., Zhang, K., Wang, E.K., Wang, J.: The potential and flux landscape theory of evolu- tion. J. Chem. Phys. 137, 065102 (2012)
-
Gardiner, C.W.: Handbook of Stochastic Methods, Stochastic Processes in Physics & Chemistry. Elsevier, New York (1985)
-
Haken, H.: Advanced Synergetics: Instability Hierarchies of Self-Organizing Systems and Devices. Springer, Berlin (1987)
-
Wang, J., Zhang, K., Lu, H.Y., Wang, E.K.: Dominant Kinetic Paths on Biomolecular Binding- Folding Energy Landscape. Phys. Rev. Lett. 96, 168101 (2006)
-
Wang, J., Zhang, K., Wang, E.: Kinetic paths, time scale, and underlying landscapes: a path inte- gral framework to study global natures of nonequilibrium systems and networks. J. Chem. Phys. 133, 125103 (2010)
-
Feng, H.D., Han, B., Wang, J.: Dominant kinetic paths of complex systems: gene networks. J Phys. Chem. Lett. 1, 1836–1840 (2010)
-
Feng, H.D., Zhang, K., Wang, J.: Non-equilibrium transition state rate theory. Chem. Sci. 5, 3761– 3769 (2014)
-
Wang, J., Xu, L., Wang, E.K., Huang, S.: The potential landscape of genetic circuits imposes the arrow of time in stem cell differentiation. Biophys. J. 99, 29–39 (2010)
-
Wang, J., Zhang, K., Lu, H.Y., Wang, E.K.: Quantifying kinetic paths of protein folding. Biophys. J. 89, 1612–1620 (2005)
-
Yan, H., Wang, J.: Quantification of motor network dynamics in Parkinson’s disease by means of landscape and flux theory. PLoS ONE 12, e0174364 (2017)
-
Yan, H., Zhang, K., Wang, J.: Physical mechanism of mind changes and tradeoffs among speed, accuracy, and energy cost in brain decision making: landscape, flux, and path perspectives. Chi- nese Phys B. 25, 078702 (2016)
-
Yan, H., Zhao, L., Hu, L., Wang, X., Wang, E., Wang, J.: Nonequilibrium landscape theory of neu- ral networks. Proc. Natl. Acad. Sci. USA 110, E4185–E4194 (2013)
-
Wang, J., Huang, B., Xia, X., Sun, Z.: Funneled landscape leads to robustness of cell networks: yeast cell cycle. PLOS Comput. Biol. 2, e147 (2006)
-
Xu, L.F., Shi, H.L., Feng, H.D., Wang, J.: The energy pump and the origin of the non-equilibrium flux of the dynamical systems and the networks. J. Chem. Phys. 136, 165102 (2012)
-
Gérard, C., Goldbeter, A.: Temporal self-organization of the cyclin/Cdk network driving the mam- malian cell cycle. Proc. Natl. Acad. Sci. USA 106, 21643–21648 (2009)
-
Lv, C., Li, X., Li, F., Li, T.: Energy landscape reveals that the budding yeast cell cycle is a robust and adaptive multi-stage process. PLoS Comput. Biol. 11, e1004156 (2015)
-
Ferrell, J., Tsai, T.C., Yang, Q.: Modeling the cell cycle: why do certain circuits oscillate? Cell
-
144, 874–885 (2011)
-
Bo, H., Jin, W.: Quantifying robustness and dissipation cost of yeast cell cycle network: the fun- neled energy landscape perspectives. Biophys. J. 92, 3755–3763 (2007)
-
Yang, Q., Ferrell, J.E., Jr.: The Cdkl-APC/C cell cycle oscillator circuit functions as a time delayed, ultra sensitive switch. Nat. Cell Biol. 15, 519 (2013)
-
Tsai, Y.C., Theriot, J.A., Ferrell, J.E.: Changes in oscillatory dynamics in the cell cycle of early
-
Xenopus laevis embryos. PLoS Biol. 12, e1001788 (2014)
-
Li, F., Long, T., Lu, Y., Ouyang, Q., Tang, C.: The yeast cell-cycle is robustly designed. Proc. Natl. Acad. Sci. USA 101, 4781–4786 (2004)
-
Li, C.H., Wang, J.: Landscape and flux reveal a new global view and physical quantification of mammalian cell cycle. Proc. Natl. Acad. Sci. USA 111, 14130–14135 (2014)
-
Han, B., Wang, J.: Quantifying robustness and dissipation cost of yeast cell cycle network: The funneled energy landscape perspectives. Biophys. J. 92, 3755–3763 (2007)
-
Wang, J., Li, C.H., Wang, E.K.: Potential and flux landscapes quantify the stability and robustness of budding yeast cell cycle network. Proc. Natl. Acad. Sci. USA 107, 8195–8200 (2010)
-
Zhang, K., Wang, J.: Exploring the underlying mechanisms of the Xenopus laevis embryonic cell cycle. J. Phys. Chem. B 122, 5487–5499 (2018)
-
Kauffman, S.: Homeostasis and differentiation in random genetic control networks. Nature 224, 177–178 (1969)
-
Kauffman, S.: Differentiation of malignant to benign cells. J. Theor. Biol. 31, 429–451 (1971)
-
-
Zhang, B., Wolynes, P.G.: Stem cell differentiation as a many-body problem. Proc. Natl. Acad. Sci. USA 111, 10185–10190 (2014)
-
Waddington, C.H.: The strategy of the genes. A discussion of some aspects of theoretical biology. With an appendix by H. Kacser (1957)
-
Chickarmane, V., Peterson, C.: A computational model for understanding stem cell, trophectoderm and endoderm lineage determination. PLoS ONE 3, e3478 (2008)
-
Jiang, J.M., Chan, Y.S., Loh, Y.H., Cai, J., Tong, G.Q., Lim, C.A., Robson, P., Zhong, S., Ng, H.H.: A core Klf circuitry regulates self-renewal of embryonic stem cells. Nat. Cell Biol. 10, 353–360 (2008)
-
Sui, H., Ernberg, I., Kauffman, S.: Cancer attractors: a systems view of tumors from a gene network dynamics and developmental perspective. Semin. Cell Dev. Biol. 20, 869–876 (2009)
-
Li, C.H., Wang, J.: Quantifying cell fate decisions for differentiation and reprogramming of a human stem cell network: landscape and biological paths. PLOS Comput. Biol. 9, e1003165 (2013)
-
Wang, J., Zhang, K., Xu, L., Wang, E.: Quantifying the Waddington landscape and biological paths for development and differentiation. Proc. Natl. Acad. Sci. USA 108, 8257–8262 (2011)
-
Zhang, K., Wang, J.: Exploring the underlying mechanisms of the coupling between cell differentia- tion and cell cycle. J. Phys. Chem. B 123, 3490–3498 (2019)
-
Li, C.H., Wang, J.: Quantifying Waddington landscapes and paths of non-adiabatic cell fate decisions for differentiation, reprogramming and transdifferentiation. J. R. Soc. Interface 10, 20130787 (2013)
-
Feng, H.D., Wang, J.: A new mechanism of stem cell differentiation through slow binding/unbinding of regulators to genes. Sci. Rep. 2, 550 (2012)
-
Weinberg, H.: Hallmarks of cancer: the next generation. Cell 144, 646–674 (2011)
-
Hanahan, D., Weinberg, R.A.: The hallmarks of cancer. Cell 100, 57–70 (2000)
-
Gatenby, R.A., Vincent, T.L.: An evolutionary model of carcinogenesis. Cancer Res. 63, 6212–6220 (2003)
-
Wang, E., Lenferink, A., Connor-McCourt, M.O.: Cancer systems biology: exploring cancer-associated genes on cellular networks. Cell Mol. Life Sci. 64, 1752–1762 (2007)
-
Ao, P., Galas, D., Hood, L., Zhu, X.M.: Cancer as robust intrinsic state of endogenous molecular- cellular network shaped by evolution. Med Hypotheses. 70, 678–684 (2008)
-
Bar-Yam, Y., Harmon, D., Bivort, B.D.: Systems biology. Attractors and democratic dynamics. Sci- ence 323, 1016 (2009)
-
Basan, M., Risler, T., Joanny, J., Sastre Garau, X., Prost, J.: Homeostatic competition drives tumor growth and metastasis nucleation. Hfsp J. 3, 265–272 (2009)
-
Creixell, P., Schoof, E.M., Erler, J.T., Linding, R.: Navigating cancer network attractors for tumor- specific therapy. Nat. Biotechnol. 30, 842–848 (2012)
-
Lu, M., Jolly, M.K., Levine, H., Onuchic, J.N., Ben-Jacob, E.: MicroRNA-based regulation of epithe- lial-hybrid-mesenchymal fate determination. Proc. Natl. Acad. Sci. USA 110, 18144–18149 (2013)
-
Yu, C., Liu, Q., Chen, C., Yu, J., Wang, J.: Landscape perspectives of tumor, EMT, and development. Phys. Biol. 16, 051003 (2019)
-
Yu, C., Wang, J.: A physical mechanism and global quantification of breast cancer. PLoS ONE 11, e0157422 (2016)
-
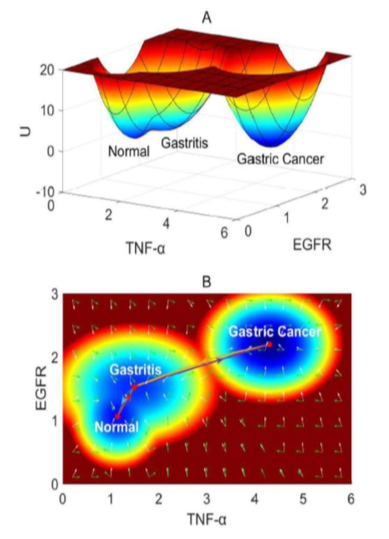
Yu, C., Xu, H., Wang, J.: A global and physical mechanism of gastric cancer formation and progres- sion. J. Theor. Biol 520, 110643 (2021)
-
Li, C.H., Wang, J.: Quantifying the landscape for development and cancer from a core cancer stem cell circuit. Cancer Res. 75, 2607–2618 (2015)
-
Li, W.B., Wang, J.: Uncovering the underlying mechanism of cancer tumorigenesis and development under an immune microenvironment from global quantification of the landscape. J. R. Soc. Interface. 14, 20170105 (2017)
-
Chen, C., Wang, J.: A physical mechanism of cancer heterogeneity. Sci. Rep. 6, 20679 (2015)
-
Li, C., Wang, J.: Quantifying the underlying landscape and paths of cancer. J. R. Soc. Interface. 11, 20140774 (2014)
-
Kang, X., Li, C.: A dimension reduction approach for energy landscape: identifying intermediate states in metabolism-MT network. Adv. Sci. 8, 2003133 (2021)
-
Hopfield, J.J.: Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 79, 2554–2558 (1982)
-
Shadlen, M.N., Newsome, W.T.: Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. J. Neurophysiol. 86, 1916 (2001)
-
Roitman, J.D., Shadlen, M.N.: Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. J. Neurosci. 22, 9475–9489 (2002)
-
Abbott, L.F.: Theoretical neuroscience rising. Neuron 60, 489–495 (2008)
-
-
Yan, H., Wang, J.: Non-equilibrium landscape and flux reveal the stability-flexibility-energy tradeoff in working memory. PLOS Comp. Biol. 16, e1008209 (2020)
-
Han, Y., Wang, J.: Non-equilibrium landscape and flux reveal how the central amygdala circuit gates passive and active defensive responses. J. R. Soc. Interface. 16, 20180756 (2019)
-
Fisher, R.A.: The Genetical Theory of Natural Selection. Oxford University Press, Oxford (1930)
-
Rice, S.H.: Evolutionary Theory: Mathematical and Conceptual Foundations. Sinauer Associates, Massachusetts (2004)
-
Wright, S.: Statistical genetics and evolution. B. Am. Math. Soc. 48, 223–246 (1941)
-
Shraiman, R.A.N., Boris, I.: Statistical genetics and evolution of quantitative traits. Rev. Mod. Phys.
-
83, 1283–1300 (2011)
-
Valen, L.V.: A new evolutionary law. Evolut. Theory 1, 1–30 (1973)
-
Tokuda, N., Terada, T.P., Sasai, M.: Dynamical modeling of three-dimensional genome organization in interphase budding yeast. Biophys. J. 102, 296–304 (2012)
-
others, E. P. C. a.: An integrated encyclopedia of DNA elements in the human genome OPEN. Nature
-
489, 57–74 (2012)
-
Pruitt, K.D., Tatusova, T., Maglott, D.R.: NCBI Reference Sequences (RefSeq): a curated non-redundant sequence database of genomes, transcripts and proteins. Nucleic Acids Res. 33, D501–D504 (2005)
-
Lieberman-Aiden, E., Berkum, N.V., Williams, L., Imakaev, M., Ragoczy, T., Telling, A., Amit, I., Lajoie, B.R., Sabo, P.J., Dorschner, M.O.: Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science 326, 289 (2009)
-
Pierro, M., Cheng, R.R., Aiden, E.L., Wolynes, P.G., Onuchic, J.N.: De novo prediction of human chromosome structures: epigenetic marking patterns encode genome architecture. Proc. Natl. Acad. Sci. USA 114, 201714980 (2017)
-
Yang, H., Luan, Y., Liu, T., Lee, H.J., Yue, F.: A map of cis-regulatory elements and 3D genome structures in zebrafish. Nature 588, 337–343 (2020)
-
Chu, X., Wang, J.: Conformational state switching and pathways of chromosome dynamics in cell cycle. Appl. Phys. Rev. 7, 031403 (2020)
-
Chu, X., Wang, J.: Insights into the molecular mechanisms of cell fate decision making processes from chromosome structural dynamics. bioRxiv, 2021.05.09.443292 (2021)
-
Chu, X., Wang, J.: Deciphering the molecular mechanism of the cancer formation by chromosome structural dynamics. bioRxiv, 2021.02.15.431330 (2021)
-
Nicolis, G., Prigogine, I.: Self-Organization in Nonequilibrium Systems. Wiley, New York (1977)
-
Fang, X., Liu, Q., Christopher, B., Zach, H., Han, W., Jin, W., Jie, X.: Cell fate potentials and switch- ing kinetics uncovered in a classic bistable genetic switch. Nat. Commun. 9, 2787 (2018)
-
Jiang, Z., Tian, L., Fang, X., Zhang, K., Liu, Q., Dong, Q., Wang, E., Wang, J.: The emergence of the two cell fates and their associated switching for a negative auto-regulating gene. BMC Biol. 17, 49 (2019)
-
Ptashne, M.: A Genetic Switch: Phage Lambda Revisited. Cold Spring Harbor Laboratory Press, Cold Spring Harbor (2004)
-
Liu, Q., Wang, J.: Quantifying the flux as the driving force for nonequilibrium dynamics and ther- modynamics in non-Michaelis–Menten enzyme kinetics. Proc. Natl. Acad. Sci. USA 117, 923–930 (2019)
-
Nussinov, R., Wolynes, P.G.: A second molecular biology revolution? The energy landscapes of bio- molecular function. Phys. Chem. Chem. Phys. 16, 6321–6322 (2014)
-
Lapidus, S., Han, B., Wang, J.: Intrinsic noise, dissipation cost, and robustness of cellular networks: The underlying energy landscape of MAPK signal transduction. Proc. Natl. Acad. Sci. USA 105, 6039–6044 (2008)
-
Wang, J., Zhang, K., Wang, E.: Robustness and dissipation of mitogen-activated protein kinases sig- nal transduction network: Underlying funneled landscape against stochastic fluctuations. J. Chem. Phys. 129, 10B602-109 (2008)
-
Li, W., Wang, J.: Uncovering the underlying mechanisms of cancer metabolism through the land- scapes and probability flux quantifications. iScience 23, 101 (2020)
-
Luo, X., Xu, L., Han, B., Wang, J., Morozov, A.V.: Funneled potential and flux landscapes dictate the stabilities of both the states and the flow: Fission yeast cell cycle. PLOS Comput. Biol. 13, e1005710 (2017)
-
Li, W., Wang, J.: Uncovering the underlying physical mechanism for cancer-immunity of MHC class I diversity. Biochem. Biophys. Res. Commun. 504, 532–537 (2018)
-
Zhao, L., Wang, J.: Uncovering the mechanisms of Caenorhabditis elegans ageing from global quanti- fication of the underlying landscape. J. R. Soc. Interface. 13, 20160421 (2016)
-
Li, W., Zhao, L., Wang, J.: Searching for the mechanisms of mammalian cellular aging through underlying gene regulatory networks. Front. Genet. 11, 593 (2020)
-
Li, C., Wang, E., Wang, J., Sui, H.: Potential landscape and probabilistic flux of a predator prey net- work. PLoS ONE 6, e17888 (2011)
-
Xu, L., Patterson, D., Staver, A.C., Levine, S.A., Wang, J.: Unifying deterministic and stochastic ecological dynamics via a landscape-flux approach. Proc. Natl. Acad. Sci. USA 118, e2103779118 (2021)
-
Zhang, K., Wang, J.: Landscape and flux theory of non-equilibrium open economy. Physica A 482, 189–208 (2017)
-
Zhang, K., Liu, J., Wang, E.K., Wang, J.: Quantifying risks with exact analytical solutions of deriva- tive pricing distribution. Physica A 471, 757–766 (2017)
-
Zhang, F., Xu, L., Wang, J.: The dynamic and thermodynamic origin of dissipative chaos: chemical Lorenz system. Phys. Chem. Chem. Phys. 22, 27896–27902 (2020)
-
Li, C., Wang, E., Wang, J.: Potential flux landscapes determine the global stability of a Lorenz chaotic attractor under intrinsic fluctuations. J. Chem. Phys. 136, 6681–7127 (2012)
-
Wu, W., Wang, J.: Nonequilibrium thermodynamics of turbulence and stochastic fluid systems. New J. Phys. 22, 113017 (2020)
-
Wu, W., Zhang, F., Wang, J.: Potential landscape and flux field theory for turbulence and nonequilib- rium fluid systems. Ann Phys-New York. 389, 63–101 (2018)
-
Zhang, Z., Wang, J.: Curl flux, coherence, and population landscape of molecular systems: Nonequi- librium quantum steady state, energy (charge) transport, and thermodynamics. J. Chem. Phys. 140, 245101 (2014)
-
Zhang, Z., Wang, J.: Origin of long-lived coherence and excitation dynamics in pigment-protein com- plexes. Sci. Rep. 6, 37629 (2015)
-
Zhang, Z., Wang, J.: Vibrational and coherence dynamics of molecules. Phys. Chem. Chem. Phys. 17, 23754–23760 (2015)
-
Zhang, Z., Wang, J.: Shape, orientation and magnitude of the curl quantum flux, the coherence and the statistical correlations in energy transport at nonequilibrium steady state. New J. Phys. 17, 093021 (2015)
-
Zhang, Z., Wang, J.: The assistance of molecular vibrations on coherent energy transfer in photosyn- thesis from the view of quantum heat engine. J. Phys. Chem. B 119, 4662–4667 (2015)
-
Zhang, Z., Wang, J.: Landscape, kinetics, paths and statistics of curl flux, coherence, entanglement and energy transfer in non-equilibrium quantum systems. New J. Phys. 17, 043053 (2015)
-
Wang, Z.H., Wu, W., Cui, G., Wang, J.: Coherence enhanced quantum metrology in a nonequilibrium optical molecule. New J. Phys. 20, 033034 (2018)
-
Wang, X., Zhang, Z., Wang, J.: Excitation energy transfer under strong laser drive. Phys. Rev. A. 103, 013516 (2021)
-
Zhang, K., Wu, W., Wang, J.: The influence of equilibrium and nonequilibrium environments on the macroscopic realism through Leggett-Garg inequality. Phys. Rev. A. 101, 052334 (2020)
-
Zhang, K., Wang, J.: Entanglement versus Bell nonlocality of quantum nonequilibrium steady states. Quantum Inf. Process. 20, 1–32 (2021)
-
Wang, Z.H., Wu, W., Wang, J.: Steady-state entanglement and coherence of two coupled qubits in equilibrium and nonequilibrium environments. Phys. Rev. A. 99, 042320 (2019)
-
Li, R., Wang, J.: Thermodynamics and kinetics of Hawking-Page phase transition. Phys. Rev. D. 102, 024085 (2020)
-
Li, R., Wang, J.: Hawking radiation and P v criticality of charged dynamical (Vaidya) black hole in anti-de Sitter space. Phys. Lett. B. 813, 136035 (2021)
-
Li, R., Wang, J., Wang, Y. Q., Zhang, H.: Nonequilibrium dynamical transition process between excited states of holographic superconductors. J. High Energ. Phys. 59 (2020)
-
Li, R., Zhang, K., Wang, J.: Thermal dynamic phase transition of Reissner-Nordström Anti-de Sitter Black Holes on free energy landscape. J High Energ Phys. 90 (2020)
-
Wang, H., Wang, J.: The Nonequilibrium Back Reaction of Hawking Radiation to a Schwarzschild Black Hole. Adv. High Energy Phys. 9102461 (2020)
-
Wang, H., Li, X., Wang, J.: Quantifying the potential and flux landscapes for nonequilibrium multi- verse, a new scenario for time arrow. J. High Energ. Phys. 2021, 105 (2021)
-
Whitehead, A.N.: Process and Reality. Cambridge University Press, Cambridge (1929)
-
Kaipayil, J.: Relationalism: A Theory of Being. JIP Publications, Bangalore (2009)
-
Pamanabhan, T.: Gravitation, Foundations and Frontiers. Cambridge University Press, Cambridge (2012)
-
Jacobson, T.: Thermodynamics of spacetime: the Einstein equation of state. Phys. Rev. Lett. 75, 1260–1263 (1995)
-
Verlinde, E.: On the origin of gravity and the laws of Newton. J. High Energ. Phys. 2011, 029 (2011)
-
Zeng, Q., Wang, J.: Information landscape and flux, mutual information rate decomposition and con- nections to entropy production. Entropy-Switz 19, 678 (2017)
-
Zeng, Q., Wang, J.: Non-Markovian nonequilibrium information dynamics. Phys. Rev. E 98, 032123 (2018)
-
Zeng, Q., Wang, J. : New fluctuation theorems on Maxwell’s demon. Sci. Adv. eabf1807 (2021)
-
Maldacena, J., Susskind, L.: Cool horizons for entangled black holes. Fortschr. Phys. 61, 781–811 (2013)
-
Feng, H., Wang, J.: Potential and flux decomposition for dynamical systems and nonequilibrium ther- modynamics: Curvature, gauge field, and generalized fluctuation-dissipation theorem. J. Chem. Phys. 135, 234511 (2011)
-
Gardiner, C.W.: Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences, 3rd edn. Springer, Berlin (2004)
-
Bialek, W.: Biophysics: Searching for Principles. Princeton University Press, Princeton (2012)
-
Wu, W., Wang, J.: Landscape framework and global stability for stochastic reaction diffusion and general spatially extended systems with intrinsic fluctuations. J. Phys. Chem. B 117, 12908–12934 (2013)
-
Wu, W., Wang, J.: Potential and flux field landscape theory. I. Global stability and dynamics of spa- tially dependent non-equilibrium systems. J. Chem. Phys. 139, 121920 (2013)
-
Wu, W., Wang, J.: Potential and flux field landscape theory. II. Non-equilibrium thermodynamics of spatially inhomogeneous stochastic dynamical systems. J. Chem. Phys. 141, 105 (2014)
-
Zhang, B., Wolynes, P.: Topology, structures, and energy landscapes of human chromosomes. Proc. Natl. Acad. Sci. USA 112, 6062–6067 (2015)
-
Publisher’s Note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.



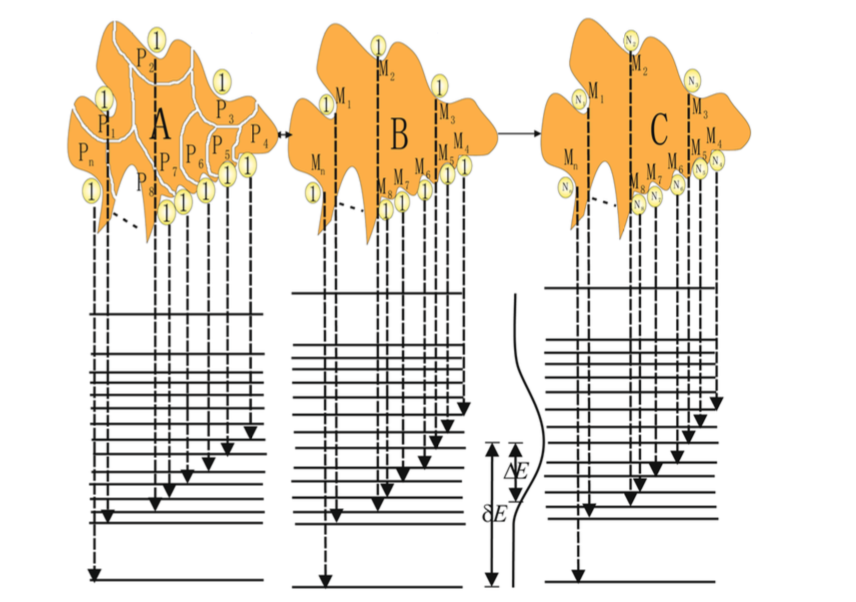
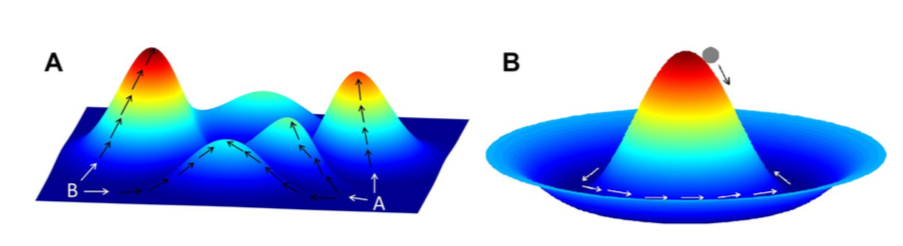
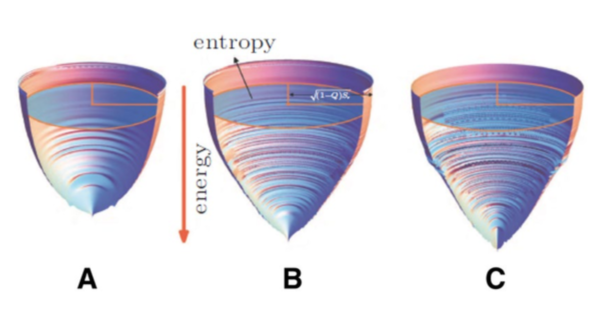 图1. 蛋白质折叠的能量漏斗景观。漏斗深度对应于能量,垂直于能量轴的截面面积等于构型熵。能量和构型熵都根据蛋白质尺寸做了归一化[19]。根据能量景观理论,由于自然进化选择,折叠景观总体偏向于自然折叠状态。
图1. 蛋白质折叠的能量漏斗景观。漏斗深度对应于能量,垂直于能量轴的截面面积等于构型熵。能量和构型熵都根据蛋白质尺寸做了归一化[19]。根据能量景观理论,由于自然进化选择,折叠景观总体偏向于自然折叠状态。