临界的鸟群如何灵活飞舞？统计场论方法研究鸟群集体行为

摘要

鸟类的飞行受空气动力学和生物力学约束，因此鸟群中个体的速度涨落是有限的。然而速度涨落的空间相关性是无标度的，即作用范围涉及整个鸟群，这一性质与系统对外界扰动的集体响应能力有关。无标度相关性和有限的速度涨落，为控制个体速度的机制施加了相矛盾的约束：如果提升相关性的因素会放大速度涨落，反之亦然。近日发表于 Nature Communications 一项最新研究采用统计场论方法，提出忽略小涨落且强烈抑制大涨落的边际速度约束，能够调和无标度相关性和符合生理的群体速度。本文将这些理论预测与规模跨越两个以上数量级的椋鸟群实地实验数据对比，证实了边际速度约束的有效性。

研究领域：集体行为，临界，无标度相关性，统计场论

张澳 | 作者

梁金 | 审校

邓一雪 | 编辑

论文题目：

Marginal speed confinement resolves the conflict between correlation and control in collective behaviour

论文地址：

https://www.nature.com/articles/s41467-022-29883-4

椋鸟群是集体行为研究的典型对象。Cavagna与Parisi于2010年的研究发现了椋鸟群速度涨落的相关性具有无标度的特点，即速度关联长度随鸟群规模线性增长，详见往期推文《临界的鸟群与复杂系统——2021年诺奖得主Giorgio Parisi的集体行为研究》。近日，Cavagna再次发文，指出线性速度约束会使无标度相关性和有限的速度涨落出现矛盾，而边际速度约束（marginal speed confinement）可以解决这一矛盾。该结果增加了对椋鸟群集体行为动力学的认识，对集群机器人的控制有参考价值。

1. 临界的鸟群：速度关联具有无标度特性

成千上万的椋鸟聚集在天空中，灵动地变换形状，好似组成了一个更大的生命体。这种感觉在椋鸟遇到攻击或障碍时变得更加强烈。不管鸟群中的个体距离攻击者远或近，它们都能如一个整体般快速响应。这种现象的根源是什么？答案是鸟群速度涨落的无标度相关性，即鸟群中个体速度的变化统计上与所有其余个体均相关，可用如下所述的关联函数来描述。

整个鸟群朝着某个共同方向以平均速度 v 运动⁠，鸟群中诸多个体的运动速度会与这个平均速度的方向或大小有所偏离，可以计算个体速度相对平均速度的偏离之间的关联——即鸟群的速度关联函数。考虑鸟群中距离为 r 的任意两只鸟（i, j），以它们各自的运动速度分别减去平均速度，然后计算这两个相对速度的内积，并对所有距离为 r 的鸟进行平均，这一内积的平均值即为速度关联函数 C(r)。

根据鸟群规模对距离 r 进行无标度处理后，各鸟群关联函数随重标度距离 r/L 的变化落在同一直线上（图1a）。这表明对于不同大小的鸟群，关联长度（关联函数为 0 时对应的距离 r ）与鸟群的规模成正比，因而关联可以遍及整个鸟群。

图1.Cavagna团队汇总了规模从 N=10 至 N=3000 的鸟群数据，分析结果为（a）椋鸟速度涨落的相关性随距离变化在根据鸟群规模无标度处理后，落在同一条直线上；（b）（c）Φ为极化值，刻画了椋鸟个体运动方向的统一性，值为1时表示所有个体运动方向一致；（d）椋鸟个体速度的概率分布，以其均值12m/s 作为鸟群基准速度 v₀，上下波动值约为2m/s。

2. 失效的线性约束

由图1的分析结果可以看到椋鸟群行为有两个特征：即速度涨落具有无标度相关性（图1a），以及个体速度围绕鸟群基准速度有限波动（图2）。其中，鸟群基准速度受空气动力学和生物力学约束，对特定物种而言可取其平均速度作为基准速度。当以动力学规则模拟鸟群行为时，成功的模拟结果需要能同时呈现出这两个特征。

Cavagna 所用模型的动力学规则包含三部分，分别为模仿力、速度约束力与熵力。

模仿力代表了鸟群中邻近个体间速度方向及大小的相互模仿；
速度约束力代表个体速度偏离基准速度时将其回复至基准速度的约束（图2）；
熵力则代表了个体速度的随机波动，表示为正比于温度 T 的白噪声。

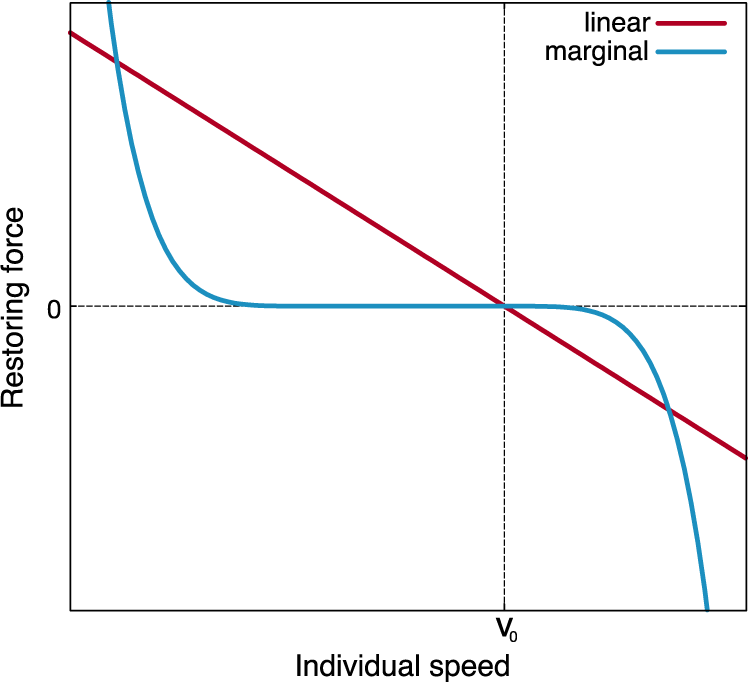
图2. 线性速度约束以与速度偏差成正比的回复力将个体速度拉回基准速度 v₀，边际速度约束忽略较小的速度偏差，强烈抑制较大的速度偏差。

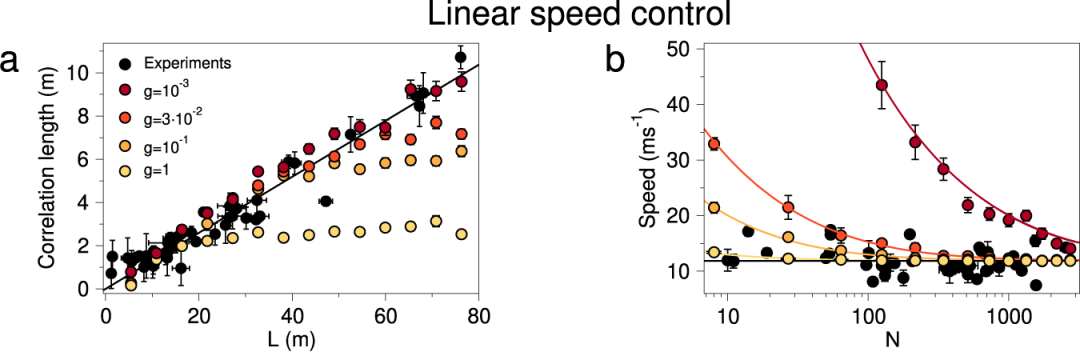
线性约束是各模型使用最多的速度约束力。若将集体行为中个体的基准速度 v₀ 比作弹簧的原长，个体的速度波动比作弹簧的压缩或拉长，则个体速度在线性约束下相对于基准速度 v₀ 的波动，与弹簧被压缩或拉长后回复至原长的方式一致，即每当个体速度 v_i 偏离基准速度 v₀ 时，个体会受到与偏离值成正比的回复力，以缓和个体速度的波动。然而，将线性约束下的模拟结果与椋鸟群的数据对比，发现线性约束无法同时产生合理的群体速度和无标度相关性，两者存在内在矛盾（见图3）。

图3. 线性速度约束的模拟结果，其中参数g为线性约束的刚度，在上述弹簧的类比中可将其理解为弹簧的弹性系数。（a）（b）两图中的现场数据（黑点）分别展示了椋鸟群的无标度相关性和有限的速度涨落。线性速度约束的模拟结果不能同时满足这两个特性。当g较小时，模拟结果能满足无标度的相关性而不能满足有限的速度涨落；当g较大时，模拟结果能满足有限的速度涨落而不能满足无标度的相关性。

3. 边际约束解决矛盾

无标度相关性和有限的速度涨落两者产生矛盾的核心在于，速度涨落的长程关联需要较弱的速度约束力，使个体速度在基准速度周围受到的约束较小，但此时熵力会推动群体速度大大超过基准速度。而边际速度约束对较小的速度涨落约束小，能够产生长程关联，对较大的速度涨落约束大，能将群体速度限制在合理的范围内，从而解决了两者的矛盾。

图4. 边际速度约束的模拟结果。（c）鸟群关联长度与鸟群规模成正比，模拟结果表现出了与真实数据一致的无标度相关性。其中，衡量噪声水平的 T 取值按模拟能产生与真实数据一致的极化值 Φ 为标准。（d）各规模鸟群的平均速度与基准速度皆一致，鸟群中个体的速度分布或涨落可见图5。

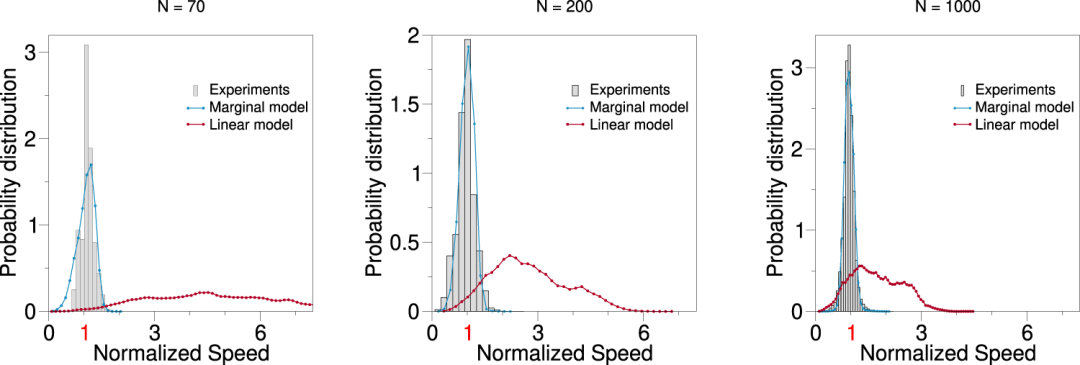
图5. 鸟群规模 N=70，200，1000 时，真实情况与边际/线性约束模拟结果中鸟群个体的速度分布。其中，边际约束参数的取值与图4一致，线性约束的参数 g 取值为 10^-3，该取值是仅有能产生无标度相关性的取值。结果显示，线性约束下的模拟结果即使在鸟群规模较大时，仍不能与真实数据较好拟合，而边际约束的模拟结果与真实数据拟合良好。

4. 生物意义与工程价值

边际速度约束除了能产生与椋鸟群现场数据相符合的数值结果外，在生物上也具有合理性。椋鸟飞行时的新陈代谢率远高于休息时，并且每日的飞行集中于半小时内，这段时间的能量消耗极大。因此，对微小速度波动产生的额外能量消耗的约束理应弱于线性约束。而速度的大幅波动则由解剖学、生理学和物理学严格限制，对其约束应该更严格。但严谨看来，边际速度约束也仅是可能的速度约束中一种较为简单的方法，后续需要收集不同物种的轨迹数据以进一步研究。

除了将研究对象扩展到除椋鸟外的其它物种，也可考虑将其延伸至人工集群系统，理论验证与技术应用相互促进。一方面，人工集群系统可以评估群体响应在多大程度上依赖无标度相关性，并可适度调整基准速度 v₀ 及个体速度相对于基准速度的波动方式，观察结果以供研究。另一方面，该研究结果指出了同时实现集群中个体长程关联与速度控制的方法，对自组织集群行为的技术实现有重大意义。

复杂科学最新论文

集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。扫描下方二维码即可一键订阅：