从国内外网络科学研究的发展趋势来看,各种各样的更复杂的网络模型和结构以及高阶相互作用动力学引起了研究者的极大兴趣,希望打破只考虑二元交互作用的局限,利用高阶网络的拓扑和几何结构来研究高阶动态过程。
在6月28日的高阶网络读书会第一期,英国玛丽女王大学应用数学教授 Ginestra Bianconi 系统性介绍了高阶网络的主要结构组合、拓扑和几何结构,以及高阶网络拓扑和动力学之间的相互作用。本文是此次报告的整理。高阶网络读书会由电子科技大学吕琳媛老师等发起,围绕高阶交互网络的基本概念、模型、方法与应用等研究进行研讨,详情见文末,欢迎感兴趣的朋友参与。
研究领域:高阶网络,单纯复形,单纯网络拓扑与几何,拓扑数据分析
Ginestra Bianconi | 讲者
高爽 | 整理
刘波、任晓龙 | 校审
邓一雪 | 编辑

个人主页:https://www.qmul.ac.uk/maths/profiles/bianconig.html
参考书籍:Higher order network: An Introduction to Simplicial Complexes
论文链接:https://pattern.swarma.org/outlink?target=http://www.cambridge.org/core_title/gb/546920
网络科学可以理解为利用关系网络来抽象表示相互作用系统,进一步用来研究系统中的复杂性。这个非常强大的框架使科学界在理解从大脑到社会的复杂系统方面取得了前所未有的进展。在过去的20年里,网络理论揭示了网络拓扑结构和动力学之间的丰富的相互作用。研究表明,复杂网络的无标度分布和小世界性质等统计特性是网络中渗流(percolation)、流行病传播(epidemic spreading)、伊辛模型(Ising model)和同步(synchronization)等过程所表现出的惊人动力学特性的主要原因。
对复杂网络的行为进行更好的理解和预测,需要更好进一步地捕捉真实数据中广泛存在的广义网络结构。高阶网络充分捕捉了两个或多个节点之间的相互作用,为描述依赖于多体相互作用的动力学过程奠定了结构基础。
高阶网络(Higher-order network)是描述两个或多个节点之间相互作用的网络结构,与网络几何、组合与统计性质、网络拓扑紧密关联,常用超图(hypergraph)和单纯复形(simplicial complex)来表示。接下来从概念入手,了解高阶网络结构。
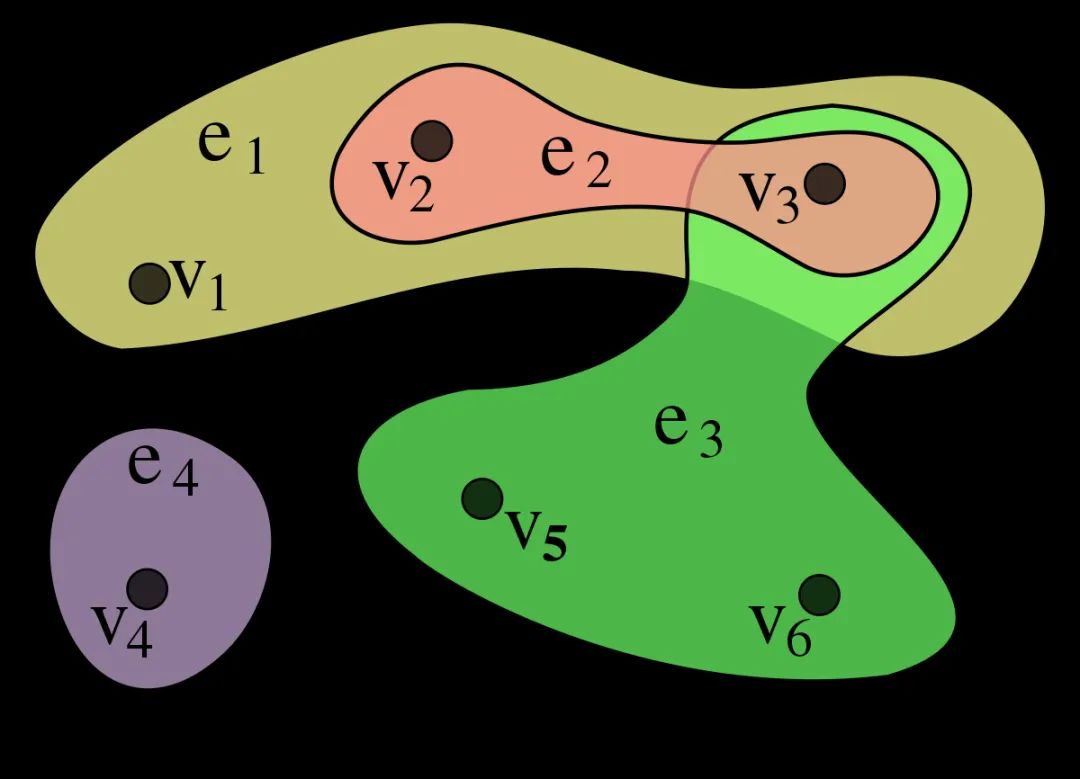
· 超边(Hyperedges):是具有相互作用的节点集合。如图1,两个节点连接一条连边,形成2-超边,以此类推,m个节点可以得到m-超边,表示m个节点之间的交互。
· 超图(Hypergraphs):超图G是由n个节点的集合V和超边的集合E定义,其中(m+1)-超边表示m+1个节点的集合,利用超边来描述节点间的多体交互。所以,每个由节点子集形成的超边可以属于也可以不属于超图。
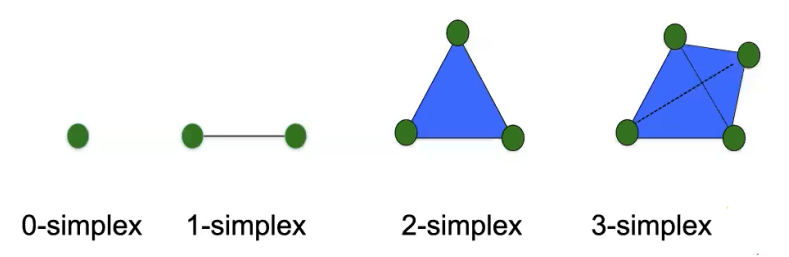
· 单纯形(Simplex):也可称为单形,一个d维单纯形(也表示为d-单形)是由一组(d+1)相互作用的节点形成的。它描述了节点间的多体交互,并允许单形的拓扑和几何解释。例如,节点是0-单纯形,链接是1-单纯形,三角形是2-单纯形,四面体是3-单纯形,以此类推。
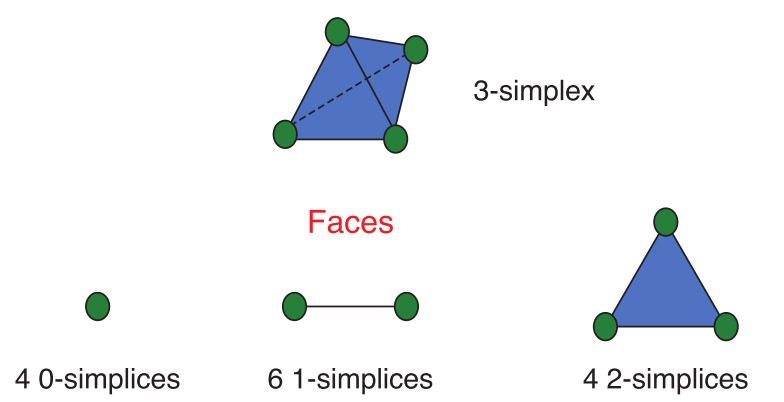
· 单形的面(Faces):d维单形的面是由单形的节点的适当子集构成的单形。在图3中,刻画了四面体的面。3维单纯形的面包含:4个 0-单纯形,6个 1-单纯形,4个 2-单纯形。
· 单纯复形(Simplicial complex):又称复形,是一个由单纯形组成的集合,每个单纯形的面都是此集合中的元素,其维度为该集合中最大维度单纯形的维度。
用更严格的数学术语来说,单纯形K是满足以下两个条件的单纯形集:(a)如果单纯形属于单纯复形,则单纯形的任意面也包含在单纯复形中;(b)给定一个单纯复形中的两个单纯形,则它们的交点属于单纯复形,或者它们的交点为零。
值得注意的是,单纯复形与超图的区别在于单纯复形包含给定单纯形的所有子集。
· 维面(Facets):维面是单纯复形中的单形,它不是任何其他单纯形的面。因此,单纯复形完全由它的维面的序列决定。
· 纯单纯复形(Pure simplicial complex):一个纯d维单纯复形是由一组d维单形及其面构成的。因此,纯d维单纯复形只允许d维单形作为面。这意味着纯d维单纯形复形是由d维单纯形沿着它们的表面粘接而形成的。
· 单元复形(Cell complex):其具有两个性质:(a) 它由一组闭包单元组成,这意味着每个单元都被一个有限的开放单元联合覆盖;(b) 给定单元复形的两个单元,它们的交集属于单元复形,或者它们的交集是空集。
· 单纯复形骨架(Simplicial complex skeleton):d维单纯复形K中所有小于等于维度r的单纯性的集合,称为单纯复形K的r维骨架,记为Kr。如果只考虑一个单纯复形网络中的节点和连边,即为该单纯复形网络的1维骨架。
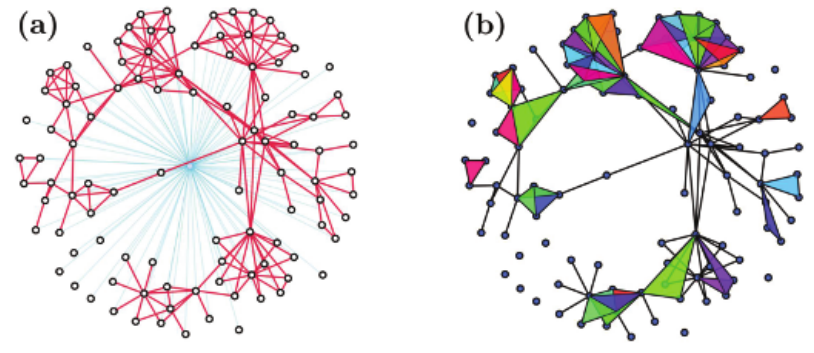
· 团复形(Clique complex):假定二元网络中的每个团都是单纯形,就可以从二元网络中生成单纯复形网络。如果给出一个只有节点和连边组成的二元网络,可以通过计算其中的所有团,把每个团作为单纯形使网络转换为一个团复形网络。
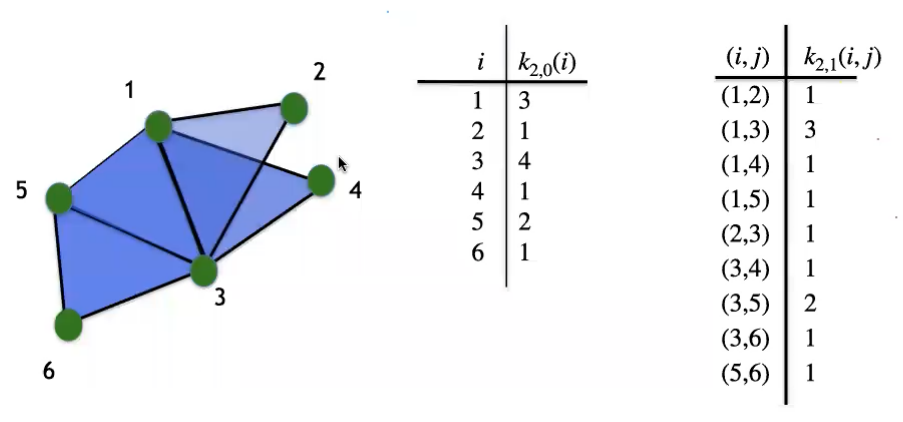
· 广义度(Generalized degrees):一个m维单纯形α的广义度kd, m(α)表示关联到该单纯形α的d维单纯形的数量。
复杂系统的网络几何是网络演化的先验前提还是网络动力学的涌现现象?在涌现几何的框架下,具有几何结构的网络是由纯粹组合的非平衡动力学生成的,即独立于网络几何结构的非平衡动力学。
具有偏好的网络几何(Network Geometry with Flavor ,NGF):是一个通用的数学框架,用于增长显示涌现的双曲网络几何的简单复合体。反映了涌现双曲几何中可直接描述的丰富的相互作用。
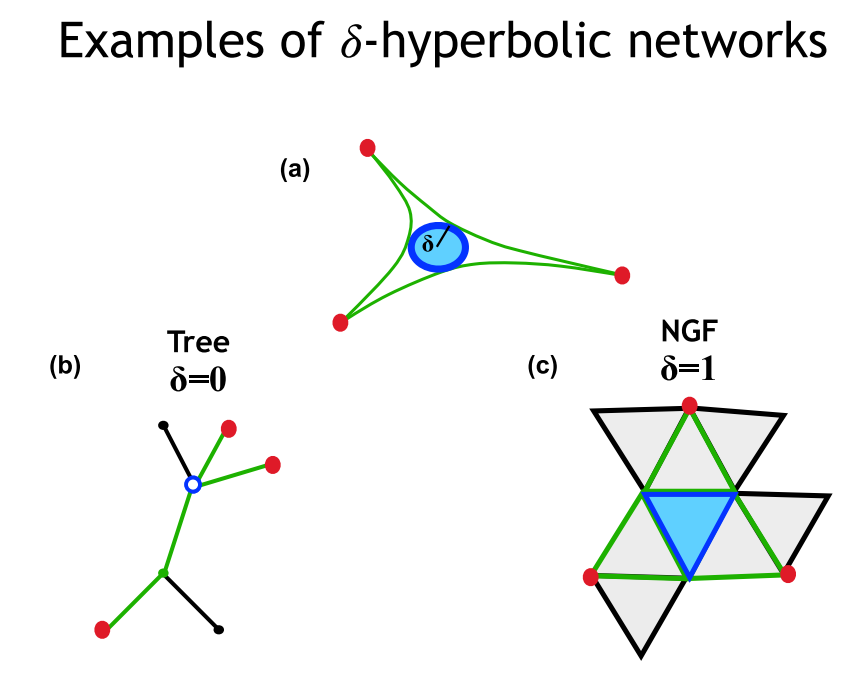
Slim Triangle Conditiond(δ–slim 三角形性质) :如果存在一个δ>0,使得对于任意的三个节点r,s,q,两两之间的最短路径为Prs,Psq,Prq,任意两个最短路径δ-邻域的并集(例如,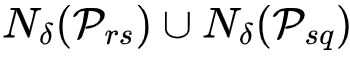 )都包括另一条路径中的节点(Prq )。δ-邻域是指到一条路径中所有节点的距离都小于等于δ的节点和连边组成的集合。
)都包括另一条路径中的节点(Prq )。δ-邻域是指到一条路径中所有节点的距离都小于等于δ的节点和连边组成的集合。
· 格罗莫夫双曲性(Gromov δ-hyperbolicity):如果一个网络服从δ-slim 三角形性质,则称这个网络是δ-双曲网络。
图5(a)是一个简单的三节点网络示意图,这三个节点组成的三角形满足δ-slim 三角形性质,因此这个网络可以被称作为δ-双曲网络。图5(b)是一个树状网络,在图中三个橙色节点满足δ-slim 三角形性质,并且三条最短路径交于蓝色节点,所以δ=0;图5(c)是一个NGF网络,其中的三个橙色节点满足δ-slim 三角形性质,并且三条最短路径之间的距离最多为1,因此此δ=1。
1. 代数拓扑
贝蒂数表示单纯复形的m维洞的数量,也等于同调群的秩。其中同调群是空间表示中的m-循环链的同调类,它们与不是(m+1)-链边界的循环链有关。
图6 贝蒂数示例图
(图中表示一个点、一个圆、一个球和一个环面及其对应的Betti数)
· 单形方向(Orientation of the simplex)
一个m维定向单纯形是一个m+1个节点的集合,它与一个方向相关联,其中δ(π)表示置换的奇偶性。
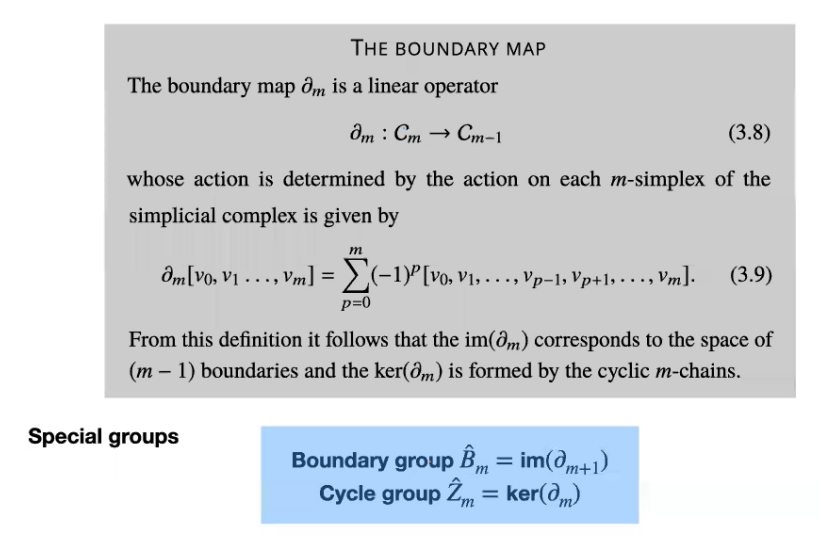
· 边界算子(Boundary operator)
边界映射是一个线性算子, 由下式给出,是由单纯复形的每个m-单形上的作用决定的。
边界算子具有边界的边界为空的性质, 这个性质直接来自边界的定义。
· 拓扑聚类(Topological clustering)
· 拓扑信号(Topological signals)
单纯复形和网络不仅可以支持定义在节点上的动态变量(信号),而且可以支持定义在高阶单纯形上的动态变量(信号),这些信号称为拓扑信号。拓扑信号包括:协作网络中的引文;给定位置的风速;海洋给定位置的海流;生物运输网络中的流量;突触信号;大脑中的边缘信号等。
关联矩阵的拉普拉斯矩阵(Graph Laplacian in terms of the incidence matrix)表示为:
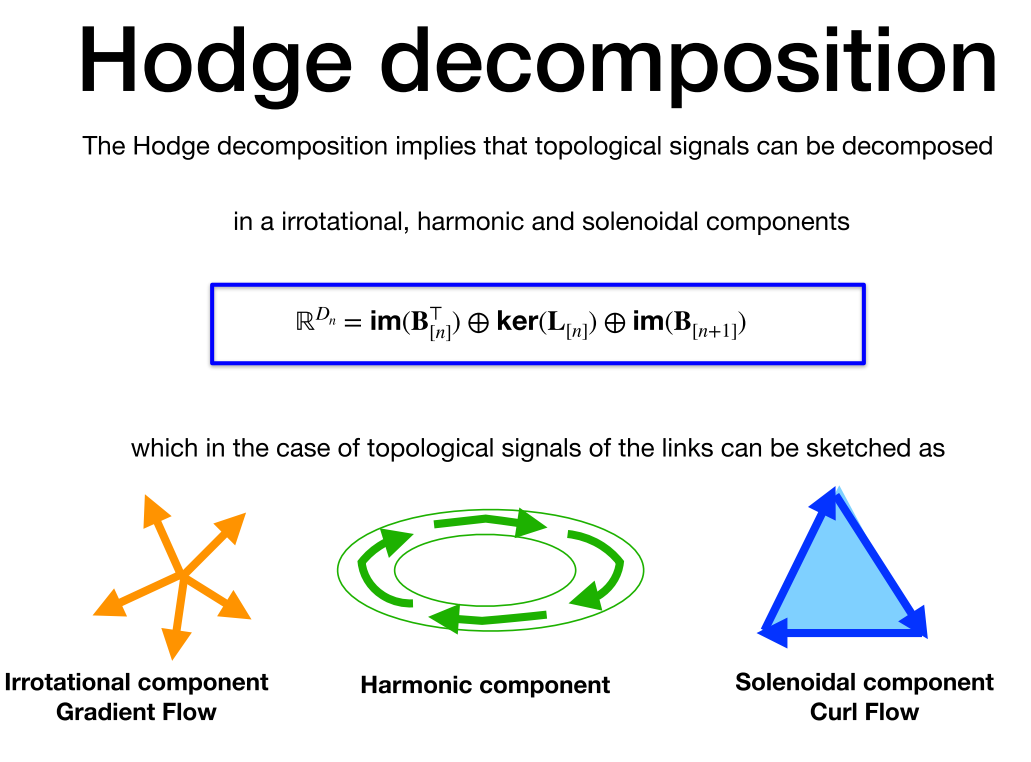
霍奇分解(Hodge decomposition):定理表示为曲面上任意一个光滑切向量场,可以被唯一地分解为三个向量场:梯度场、散度场和调和场。霍奇分解经常被用于光滑化一个矢量场,将一个不可积矢量场变得可积。
在网络中,用拓扑旋量(Topological spinor)描述网络拓扑信号的动态状态,是一个由0-协链和1-协链构成的块结构向量。
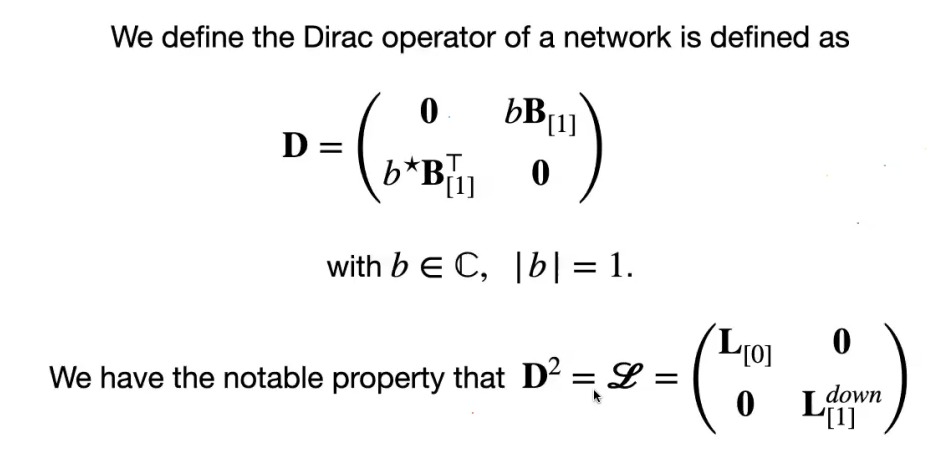
网络上的Dirac算子(Topological Dirac operator on a network)定义:
不同频率的振荡器耦合强度足够大时,会出现同步现象。在生活中的同步现象有大脑动力学,萤火虫的同时闪烁等现象。
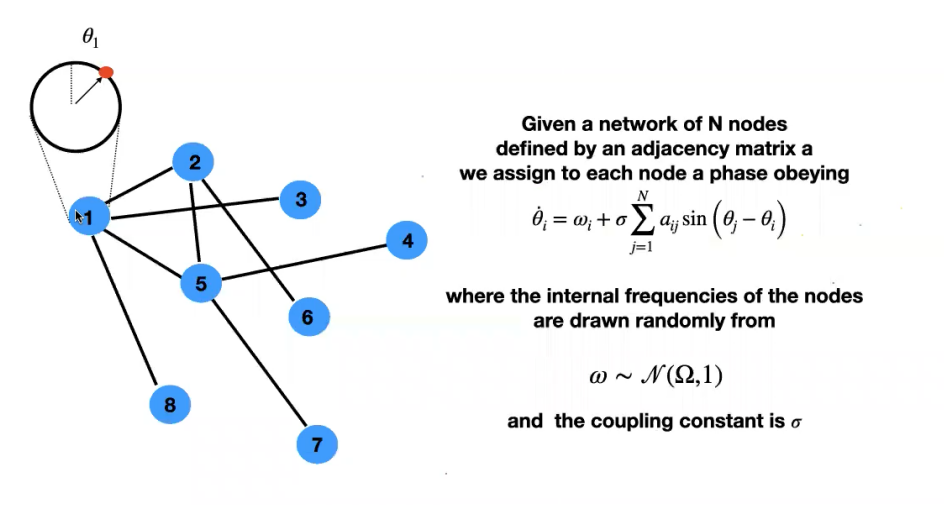
1975 年 Yoshiki Kuramoto 提出的Kuramoto模型是研究同步的一个重要参考模型. 如下经典的Kuramoto模型描述了与节点,即0-单纯形,相关的相位的同步变化。
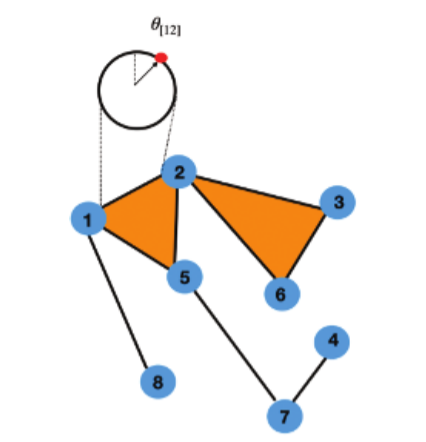
同步相变由全局序参量R刻画,当耦合常数σ较小时,相位动力学不相干;当耦合常数σ大于同步阈值σc时,发生相变。下图是由节点 (0-单纯形)、链 (1-单纯形) 和三角形 (2-单纯形,橙色阴影部分) 组成的单纯复形。
单纯复形不仅可以刻画节点 (0-单纯形) 的动力学,也可以刻画高阶单纯形的动力学。
在一个网络或单复形骨架中,与节点相关的相位θ满足如下方程,相位θ和自然频率ω如下:
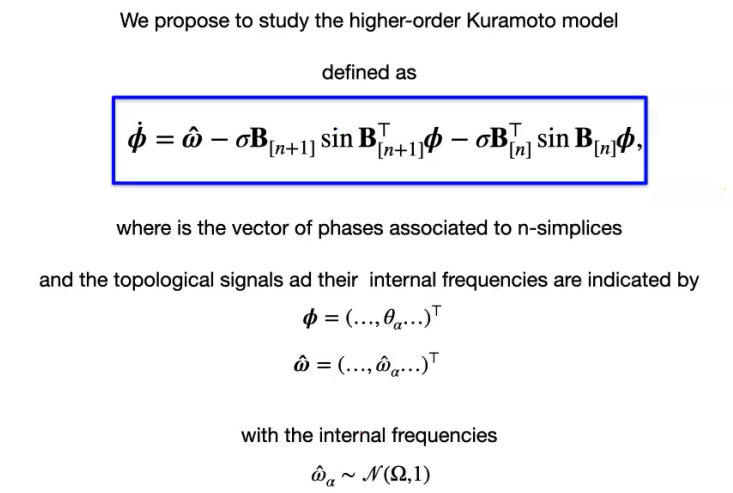
对于高阶Kuramoto模型,可以将一个振荡通量关联到每一个链路,即将相位关联到每个m维单纯形上。
所以用用关联矩阵表示高阶 Kuramoto 模型来表示单纯的同步:
非自适应耦合序参量下,拓扑同步是连续的,且σc=0。
Dirac同步利用Dirac算子在局部和拓扑上耦合不同维度的拓扑信号。Dirac同步具有热力学时滞环。其序参量包括节点信号和链路信号(投影在节点上)的线性组合。
Dirac同步导致节律相位的出现,在旋转框架中序参量自发地获得一个动力学相位,即在本征相位平均为零的框架中。其节律阶段揭示了大脑节律出现的拓扑机制。
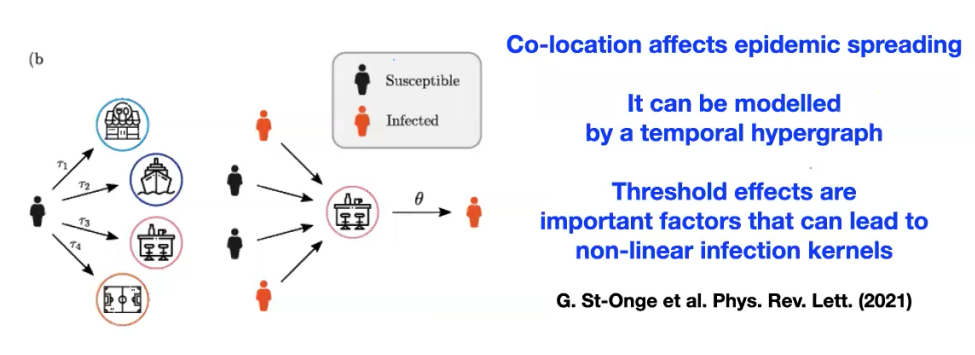
局部流行病的传播影响,可以用时间超图来模拟,阈值效应是导致非线性传染核的重要因素。
多重超图由层构成,每个层捕捉给定阶的相互作用,其中包含合作效应的高阶渗流问题是不连续的。
在本次讲座中,主讲人对高阶网络的基本概念进行了详细的讲解,并指出单纯复形是一个非常一般的数学框架。单纯复形除了可以对高阶网络进行完整的拓扑分析外,还有捕捉复杂系统的多体相互作用,揭示单纯拓扑和单纯几何在动力学重要作用的优点,为听者展示了高阶网络的整体视图。从社会过程到神经科学的众多复杂系统实例上,高阶拓扑分析具有很大潜力,高阶网络动力学已经成为目前快速发展的研究方向。
Ginestra Bianconi,英国伦敦玛丽女王大学应用数学教授,艾伦·图灵研究所的艾伦·图灵研究员。她的研究领域是统计力学和网络科学,具体包括网络理论及其跨学科应用。她是网络建模的专家,包括增长网络模型和均衡网络系综。同时也出版了关于网络动态过程的重要著作,特别是渗流研究。最近几年,她一直专注于多层网络、单纯复形、网络几何和拓扑。她是 Multilayer Networks: Structure and Function(牛津大学出版社出版) 和 Higher-order networks: An introduction to simplicial complexes (剑桥大学出版社出版) 两本书的作者。
目前,她是 JPhys Complex 期刊的主编,PlosOne 和 Scientific Reports 的编辑。2020年,她被 NetSci 学会授予 Network Scientific Fellowships,以表彰对网络科学的基础性贡献,特别是在复杂网络中玻色-爱因斯坦凝聚的提出,以及在多层网络结构和动力学方面的进展。
随着对现实世界的探索不断深入,人们发现在许多真实的复杂系统中,组成系统的个体之间不仅存在二元交互关系,也广泛存在多个体同时(或以特定顺序)进行交互,即高阶交互现象。为此,研究人员分别发展出了基于超图、单纯复形、依赖关系等的网络高阶表示模型,为复杂网络分析和研究提供了新的思路。为了促进此领域的交流与合作,我们发起了【高阶网络读书会】。
集智俱乐部读书会是面向广大科研工作者的系列论文研读活动,其目的是共同深入学习探讨某个科学议题,激发科研灵感,促进科研合作。【高阶网络读书会】由电子科技大学吕琳媛老师、任晓龙老师及中国地质大学(北京)管青老师联合发起,每周分享时间为每周四 19:30-21:30 进行,预计持续 10-12 周。这其间,我们将围绕高阶交互网络的基本概念、模型、方法与应用等研究进行研讨,本次读书会分享会按照「基础理论」+「深入理论」+「案例研讨」的模式展开。



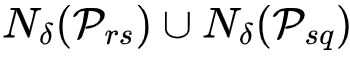 )都包括另一条路径中的节点(Prq )。δ-邻域是指到一条路径中所有节点的距离都小于等于δ的节点和连边组成的集合。
)都包括另一条路径中的节点(Prq )。δ-邻域是指到一条路径中所有节点的距离都小于等于δ的节点和连边组成的集合。