导语


高阶网络读书会由电子科技大学吕琳媛老师、任晓龙老师及中国地质大学（北京）管青老师联合发起，自2022年6月28日开始，每周四晚上19:30-21:30举办，持续时间预计 10-12周。期间，我们将围绕高阶交互网络的基本概念、模型、方法与应用等研究进行研讨，本季读书会分享会按照「基础理论」+「深入理论」+「案例研讨」的模式展开。欢迎对本话题感兴趣的朋友报名参加！详情见文末。


在高阶网络读书会第二期分享中杨荣湄和周方分别从高阶生成模型和高阶随机化模型介绍了基于结构的高阶交互网络建模，李佳旭和管炜则在第三期分享中介绍了基于依赖关系的高阶网络建模。在了解高阶网络的建模方式后，王欢将详细介绍高阶网络的重构过程。目前，高阶网络重构这一主题的相关研究还不多，如何从观测数据中重构出具有高阶关系的网络？安徽大学张海峰团队从一种最简单的单纯复形网络出发（2-单纯复形），借助由社会传染动力学和单纯形Ising动力学两种模型生成的二元时间序列数据，基于统计推断框架设计了一种纯数据驱动的方法用于重构2-单纯复形网络。王欢作为文章一作在集智俱乐部公众号上进行了文章解读，详见：单纯复形重构：如何从数据中发现复杂网络潜在高阶关系？本次分享是继论文解读后对高阶网络重构相关研究的详细汇报，将于2022年8月11日晚19:30开始，欢迎感兴趣的探索者报名直播参与进来，与社区成员共同学习！




本期分享将聚焦于高阶网络重构这一课题，围绕如下要点进行：
1. 基于二元时间序列数据的单纯复形重构

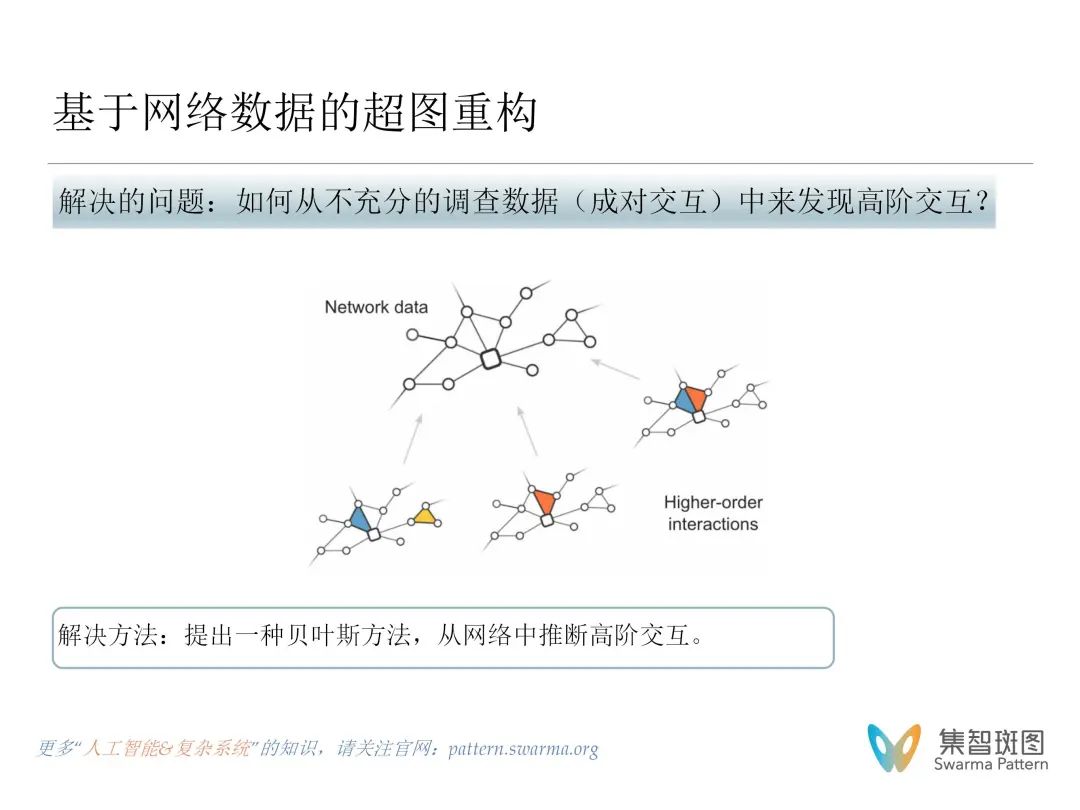
2. 基于网络数据的超图重构

基于二元时间序列数据的单纯复形重构


两走步重构法示意图


基于网络数据的超图重构


贝叶斯生成模型





跟读书会主题之间的关系




高阶网络建模，结构性质及动力学行为分析等，这些都有一个假设前提，即高阶网络的结构已知，然而在许多真实系统中，网络的高阶结构往往很难获取。高阶网络重构是指利用可观测信息推断出网络中的高阶交互关系，它能够更好地捕捉复杂系统的底层结构信息，揭示出系统中的详细拓扑连接，并提供了经验网络中局部稠密和全局稀疏性的可能解释。





报告内容简介




在社会、生物、信息等一些复杂系统中，我们往往仅能观测到状态数据或者简单结构信息，很难获得高阶交互关系，因此基于可获得信息重构网络中的高阶结构是研究复杂系统的重要途径，它能够揭示出系统中的详细拓扑连接，有助于探索复杂系统中存在的一些潜在机理。如何从这些可获取信息中推断出复杂系统中的潜在高阶结构？


为此，本期分享将聚焦于高阶网络重构这一课题，围绕如下要点进行：
1. 基于二元时间序列数据的单纯复形重构

2. 基于网络数据的超图重构


本次分享是论文解读。主要讲解两篇文章，首先介绍基于二元时间序列数据的单纯复形重构，接下来介绍基于网络数据的超图重构。



【 分享大纲】
  • 高阶网络重构问题的背景介绍
    • 高阶网络简介
    • 高阶网络上的动力学
    • 以往对网络重构问题的研究
  • 基于二元时间时间序列数据的单纯复形重构
    • 总体解决思路
    • 数据的生成
    • 概率统计方法
    • 两步走重构法
  • 基于网络数据的超图重构
    • 主要解决的问题
    • 贝叶斯生成模型
    • 后验估计


【主要涉及到的知识概念】
2-单纯复形 2-simplicial complexes
投影分量 Projection component
先验超图 Hypergraph prior
泊松随机超图模型 Poisson Random Hypergraphs Model (PRHM)
马尔可夫链蒙特卡洛 Markov Chain Monte Carlo (MCMC)

最小描述长度 Minimum description length (MDL)


【主要用的数学工具与方法】
统计推断方法
EM (Expectation-Maximization) 算法
贝叶斯方法
因子图
马尔可夫链蒙特卡洛 (MCMC) 算法

Metropolis-Hastings  (MH) 算法





主持人




任晓龙，电子科技大学长三角研究院（湖州），苏黎世联邦理工学院博士，专注于复杂系统与网络中信息挖掘的研究，利用统计物理和复杂网络的理论和方法来解决信息领域中的若干重要问题，包括系统鲁棒性、网络拆解问题，重要节点（群）挖掘，链路预测等。

实验室网站：https://linyuanlab.com/

个人主页：http://networkscience.cn/





主讲人



王欢，安徽大学数学科学学院2020级博士生，师从张海峰教授。主要研究兴趣为复杂网络上的传播动力学，网络重构，高阶网络建模与应用。

解读文献

  • Wang, Huan, et al. “Full reconstruction of simplicial complexes from binary contagion and Ising data.” Nature Communications 13.3043 (2022): 1-10.

  • Young, Jean-Gabriel, et al. “Hypergraph reconstruction from network data.” Communications Physics 4.135 (2021): 1-11.




参考文献




[1] Carletti, T., Battiston, F., Cencetti, G. & Fanelli, D. Random walks on hypergraphs. Phys. Rev. E 101, 022308 (2020). 
文章在超图中研究了随机游走，通过定义一个点选择下一步走的点主要依赖于他们共享超边的数量和大小，得到了任意两点间的转移概率及稳态时游走到每个点的概率，此外还介绍了在科学合作网中节点排序，动物分类等方面的应用。
[2]Ma, Tao, and Jinli Guo. “Study on information transmission model of enterprise informal organizations based on the hypernetwork.” Chinese journal of physics 56.5 (2018): 2424-2438.
在超图中，通过SIR模型研究了信息传播过程。
[3] Iacopini, I., Petri, G., Barrat, A. & Latora, V. Simplicial models of social contagion. Nat. Commun. 10, 1–9 (2019). 
文章在单纯复形中研究了社会传染过程，通过引入一种传染强化机制，即传染可以通过不同规模的群体之间的相互作用发生，发现了不连续相变现象，并通过平均场方法给出了理论分析及详细的稳定性分析。
[4] Dempster, Arthur P., Nan M. Laird, and Donald B. Rubin. “Maximum likelihood from incomplete data via the EM algorithm.” Journal of the Royal Statistical Society: Series B (Methodological) 39.1 (1977): 1-22. 
文章介绍了一种从不完全数据计算最大似然估计的EM算法，推导了该算法的收敛性，并给出了许多示例。
[5] Wang, Huan, et al. “Full reconstruction of simplicial complexes from binary contagion and Ising data.” Nature Communications 13.3043 (2022): 1-10. 
文章介绍了基于二元时间序列数据的单纯复形重构。
[6] Young, Jean-Gabriel, et al. “Hypergraph reconstruction from network data.” Communications Physics 4.135 (2021): 1-11. 
文章研究了如何从不充分的调查数据中来发现高阶交互的问题，作者提出了一种贝叶斯的方法，用于从网络中推断高阶交互，并分别在合成网络和经验网络中证明了所提方法对于恢复高阶相互作用的有效性。
[7] Darling, Richard WR, and James R. Norris. “Structure of large random hypergraphs.” The Annals of Applied Probability 15.1A (2005): 125-152. 
文章介绍了泊松随机超图模型。
[8] Andrieu, Christophe, et al. “An introduction to MCMC for machine learning.” Machine learning 50.1 (2003): 5-43. 
文章介绍了Metropolis-Hastings(MH)算法。
[9] MacKay, David JC, and David JC Mac Kay. Information theory, inference and learning algorithms. Cambridge university press, 2003.
这本书将通信、信号处理、数据挖掘、机器学习、模式识别、计算神经科学、生物信息学和密码学等多个领域的知识熔于一炉，内容相当广泛，包括信息传递算法、蒙特卡罗方法和变分近似，与聚类、卷积码、独立元素分析和神经网络的应用，是一本理想的自学书。
[10] Grünwald, Peter D. The minimum description length principle. MIT press, 2007.
提出最小描述长度准则—Minimum Description Length（MDL准则），目的是为了根据信息论中的基本概念来解释极大后验假设(MAP)，可以用于处理数据过拟合的问题。




直播信息




时间：

2022年8月11日（周四）晚上19:30-21:30

参与方式：

  • 集智俱乐部 B 站免费直播，扫码可预约：

扫码报名
  • 文末扫码付费参加高阶网络读书会可加入腾讯会议，可提问交流，加入群聊，获取回看地址及更多学习资料，成为集智网络科学社区种子用户，与网络科学社区的一线科研工作者沟通交流，共同推动网络科学社区的发展。


  • 视频回放地址：
    https://campus.swarma.org/course/4720
  • 前几期主题
基于依赖关系的高阶网络建模丨第三期
高阶交互网络建模 | 第二期
玛丽女王大学Ginestra Bianconi：高阶网络与动力学 | 第一期
读书会下期预告，刘波：团与洞结构及其计算，该分享仅面向读书会社区成员。


高阶网络读书会招募中


随着对现实世界探索的不断深入，人们发现在许多真实的复杂系统中，组成系统的个体之间不仅存在二元交互关系，也广泛存在多个体同时（或以特定顺序）进行交互，即高阶交互现象。为此，研究人员分别发展出了基于超图、单纯复形、依赖关系等的网络高阶表示模型，为复杂网络分析和研究提供了新的思路。为了促进此领域的交流与合作，我们发起了高阶网络读书会。

高阶网络读书会由电子科技大学吕琳媛老师、任晓龙老师及中国地质大学（北京）管青老师联合发起，第一期分享从 6月 28日（周二）20:00 开始，后续每周分享时间为每周四 19:30-21:30 进行，预计持续 10-12 周。这期间，我们将围绕高阶交互网络的基本概念、模型、方法与应用等研究进行研讨，本次读书会分享会按照「基础理论」+「深入理论」+「案例研讨」的模式展开。欢迎感兴趣的朋友参与。


本季读书会详情与报名方式请参考：
探索复杂系统高阶交互的奥秘 | 高阶网络读书会启动


点击“阅读原文”，报名直播