我们可以在没有因果关系的情况下理解耗散吗？ | 复杂性科学顶刊精选6篇

集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「集智斑图」推送论文信息。

扫描下方二维码，关注“集智斑图”服务号，即可订阅Complexity Express：

Complexity Express 一周论文精选

以下是2022年10月3日-10月9日来自Complexity Express的复杂性科学论文精选。如果Complexity Express列表中有你感兴趣的论文，欢迎点赞推荐，我们会优先组织解读~

目录：

1. 我们可以在没有因果关系的情况下理解耗散吗？

2. DeepMind 提出 AlphaTensor 加速矩阵乘法算法

3. 微生态系统中多样性与动力学相变的涌现

4. 随机游走量化城市种族隔离

5. 大脑奖励回路的神经元前景理论模型

6. 注入噪声的模拟 Ising 机实现超快统计采样与机器学习

1.我们可以在没有因果关系的情况下

理解耗散吗？

论文题目：Can We Make Sense of Dissipation without Causality?

期刊名称：Physical Review X

论文地址：https://journals.aps.org/prx/abstract/10.1103/PhysRevX.12.041001

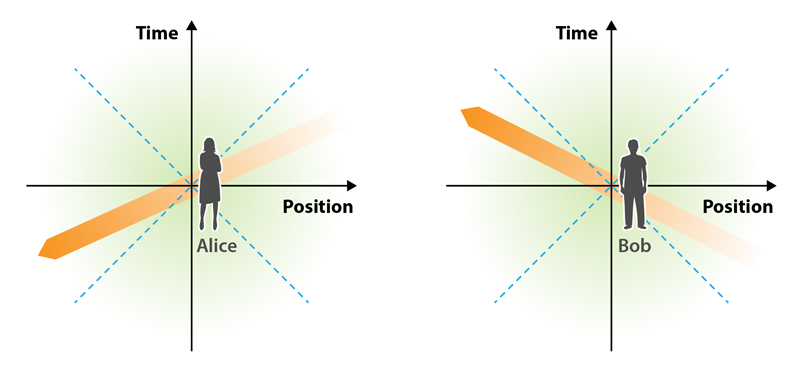
相对论使得一种反直觉事实成为可能：一个状态可以在一个参照系中是稳定的，而在另一个参照系中不稳定。因此，测试不满足洛伦兹不变性的状态的稳定性是非常麻烦的工作。

我们证明，只有当扰动能够离开光锥，两个观察者才会对一个状态是稳定还是不稳定的产生分歧。此外我们还证明，如果一个扰动离开光锥，并且其强度由于耗散而随时间变化，那么总会有两个观察者对状态的稳定性有不同看法。因此，“稳定性”是耗散理论的洛伦兹不变特性，当且仅当遵循因果关系这一原理。我们提出了针对相对论物理所有领域的物理问题的14个应用，从理论到模拟。

图：在 Alice 的参考系中（左），扰动从左向右以超光速运动，扰动强度（橙色）由于耗散而随着时间推移减小。Bob（右）相对于 Alice 处于运动中，扰动从右向左运动，其强度随时间而增加。对 Bob 和 Alice 来说，超光速扰动都落在光锥（蓝色虚线）之外，违反因果关系。这种简单的观点分析为任何相对论流体动力学理论提供了一个稳定性准则：一个理论在一个参照系中是稳定和因果的，那么在所有参照系中也是稳定的。

2.DeepMind提出

AlphaTensor加速矩阵乘法算法

论文题目：Discovering faster matrix multiplication algorithms with reinforcement learning

期刊名称：Nature

论文地址：https://www.nature.com/articles/s41586-022-05172-4#Fig2

提高基础计算算法的效率可以影响大量计算的总体速度，因而会产生广泛的影响。矩阵乘法就是这样一项基础任务，它出现在许多系统中——从神经网络到科学计算程序。使用机器学习自动发现算法提供了超越人类直觉的前景，并超越目前最好的人类设计算法。然而，自动化算法发现过程是复杂的，因为可能的算法空间无比广阔。

本文报告了一种基于 AlphaZero 的深度强化学习方法，用于发现高效且可证明正确的任意矩阵乘法算法。我们的智能体 AlphaTensor 被训练来玩一个单人游戏，目标是在有限的因子空间内找到张量分解。AlphaTensor 发现的算法性能对于许多不同大小的矩阵都超过了最先进的复杂性。特别是有限域中 4×4 矩阵的情况，其中 AlphaTensor 发现的算法在 Strassen 两层算法（Strassen’s two-level algorithm）的基础上进行了改进，据我们所知，这是自50年前发现该算法以来的第一次。

我们通过不同的用例进一步展示了 AlphaTensor 的灵活性：具有最先进复杂性的结构化矩阵乘法算法，以及通过优化特定硬件上的运行时矩阵乘法来提高实际效率。我们的结果突出了 AlphaTensor 在加速一系列问题的算法发现过程，和针对不同标准进行优化的能力。

图：AlphaTensor 框架图。

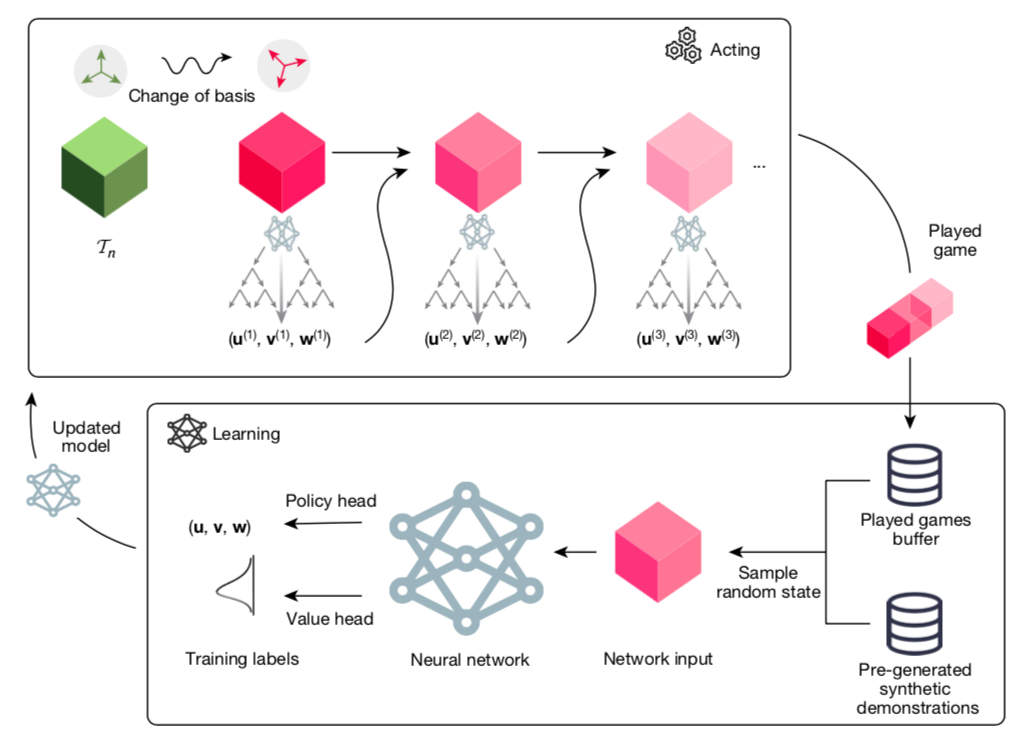
3.微生态系统中多样性

与动力学相变的涌现

论文题目：Emergent phases of ecological diversity and dynamics mapped in microcosms

期刊名称：Science

论文地址：https://www.science.org/doi/10.1126/science.abm7841

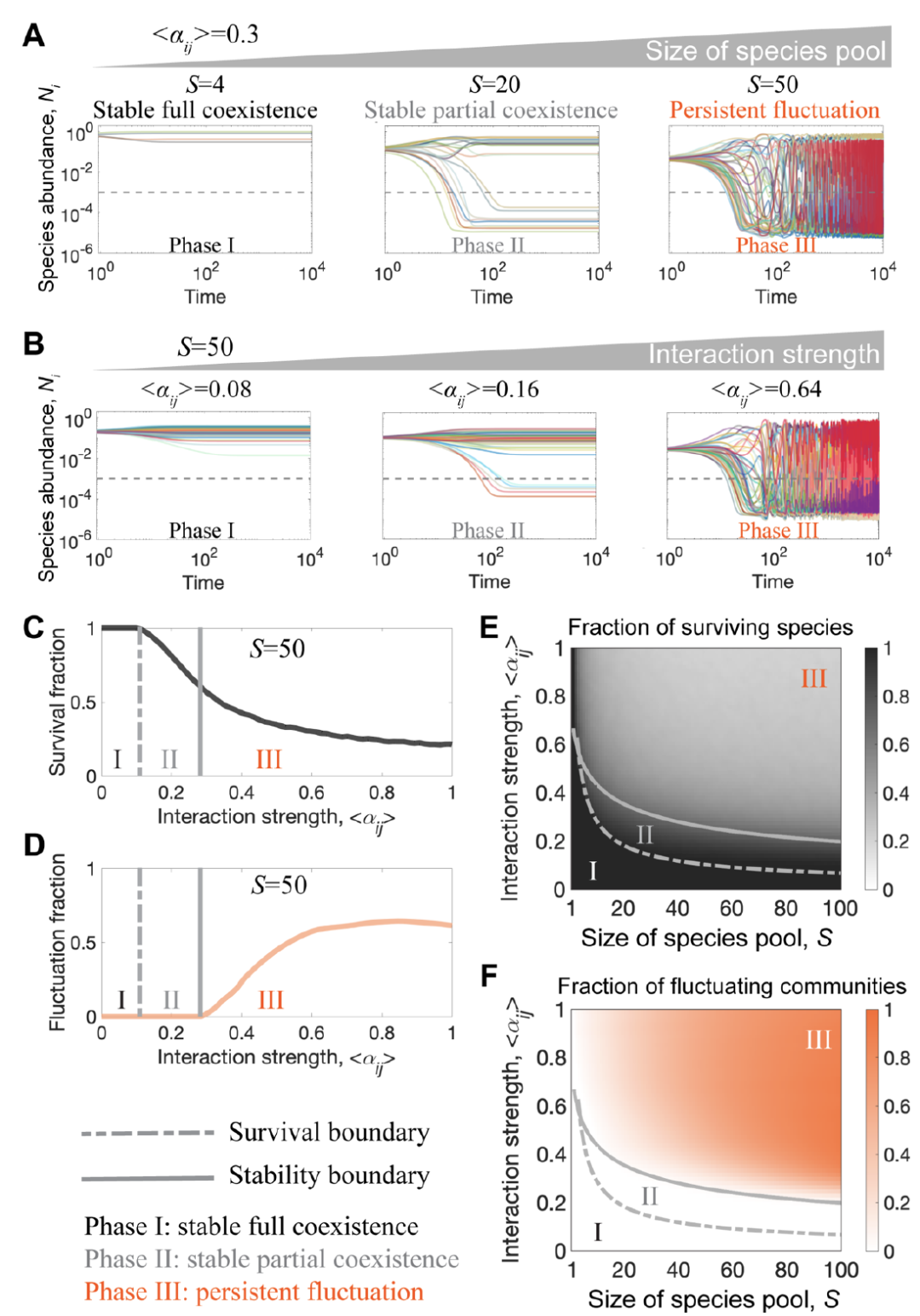
从热带雨林到肠道微生物群，生态群落承载着大量共存物种。除了高度的生物多样性，群落还表现出一系列复杂的动力学，难以在统一的框架下解释。本文利用微生物群落实验对理论预测进行了直接测试，表明一些简单的群落特征决定了群落的涌现行为。

研究表明，随着物种数量或物种间相互作用强度增加，微生物生态系统会在三个不同的动力学相之间转变，从所有物种稳定共存的平衡态，转变到部分物种稳定共存相，最终转变到物种数量随时间持续振荡相，三种相出现的顺序与理论预测一致。在固定条件下，高物种多样性和群落持续振荡之间存在正反馈。该研究结果显示了生态群落多样性和动力学的可预测的涌现模式。

图：理论预测物种数量和种间相互作用强度塑造了群落的相图。随着物种数量和种间相互作用强度增加，群落在三个涌现的动力学相之间发生相变，从所有物种稳定共存相，转变到部分物种稳定共存相，最终转变到物种数量随时间持续振荡相。

4.随机游走量化城市种族隔离

论文题目：Quantifying ethnic segregation in cities through random walks

期刊名称：Nature Communications

论文地址： https://www.nature.com/articles/s41467-022-33344-3

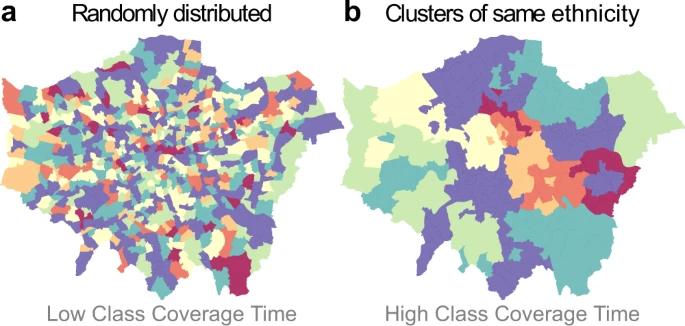
社会经济隔离对城市地区出现大规模不平等现象起着重要作用。现有的空间隔离测度大多依赖于被研究系统的规模和尺度，或者忽视大尺度的空间相关性，或者依赖特定的参数，这使得在平等的基础上比较不同系统变得困难。

基于与空间系统相关的图上随机游走轨迹的统计，本文提出一族空间分布的非参数度量。这些数据为综合空间模式中的隔离提供了一致的估计，我们使用它们来分析美国和英国大都市地区的种族隔离。研究结果表明，通过图上的扩散来度量的种族分布的空间多样性，使我们能够比较具有不同尺度、形状或特殊微观特征的城市地区的种族隔离，并显示出与社会经济匮乏的强烈关联。

图：大伦敦地区七个种族关联的虚构地图。（a）种族在全市范围内随机均匀分布，以模拟“最大”同质且不隔离的模式。（b）同样的地图，人为对种族进行聚类。在这种情况下，从集群中间开始的游走者将需要更多的时间来访问所有其他种族。这一观察导致了使用类别覆盖时间的统计数据，以量化城市地区相对于给定的感兴趣变量的隔离程度和异质性。

5.大脑奖励回路的

神经元前景理论模型

论文题目：A neuronal prospect theory model in the brain reward circuitry

期刊名称：Nature Communications

论文地址：https://www.nature.com/articles/s41467-022-33579-0

前景理论可以说是最著名的选择理论，该理论提出，人们通过两个量的乘积来计算风险前景的主观估值：一个是描述奖励主观价值的价值函数（即效用），另一个是描述人在计算期望效用时对奖励概率的主观扭曲的反S型概率权重函数（即概率权重）。前景理论是神经估值模型（neural valuation model）的明显候选。然而，尽管神经经济学（neuroeconomics）这一新兴领域在理解大脑如何做出经济决策方面取得了重大进展，但一个基本问题仍然没有得到回答，即单个神经元的放电是否真的遵循前景理论模型。神经元活动是否表征主观价值和概率权重函数的乘积？

本文以等同于人类神经成像研究的理论准确性表明，猴子在四个核心奖励相关皮层和皮层下区域的单个神经元活动表征对风险赌博的主观评价。被动观看彩票的猴子的个体神经元活动反映了对概率奖励的渴望，如同在前景理论框架中，这被参数化为效用和概率权重函数的乘积。不同的估值信号模式并不是局部的，而是分布在奖励回路的大多数部分。将这些信号聚合在一起的网络模型重构了动物选择所揭示的风险偏好和主观概率权重。因此，分布式神经编码解释了风险下主观估值的计算。

图. 简单网络模型重构猴子的主观决策统计。

6.注入噪声的模拟Ising机

实现超快统计采样与机器学习

论文题目：Noise-injected analog Ising machines enable ultrafast statistical sampling and machine learning

期刊名称：Nature Communications

论文地址：https://www.nature.com/articles/s41467-022-33441-3

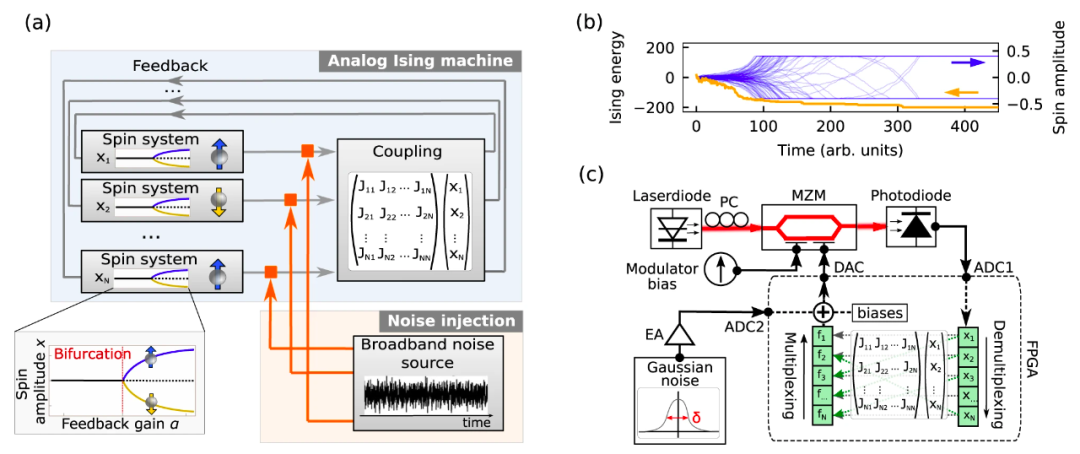
Ising 机是一种很有前景的非冯·诺伊曼计算概念，其工作原理基于这样一种认识——各种复杂的计算问题可以映射到一个简单的自旋系统，即所谓的 Ising 模型，并通过基于模拟物理系统的人工自旋网络实现。模拟 Ising 机自然倾向于演化到其最低能量构型，通过这个过程就能够找到问题的解，并突破基于冯·诺伊曼计算平台的许多限制，加速神经网络训练和组合优化问题的计算。然而，尽管各种神经网络可以用 Ising 机实现，但它们不能执行快速统计采样，这使得它们在训练神经网络方面比数字计算机效率低。

为了使用模拟 Ising 机实现高效的统计采样，并利用其固有速度加速机器学习，本文提出了一种使用模拟 Ising 机执行统计采样的通用方法，其中来自模拟噪声源的噪声被注入，驱动 Ising 机进入热平衡态。研究利用光电 Ising 机实验证明，它可以用于波尔兹曼分布的精确采样和神经网络的无监督训练，与基于软件的训练具有相同的准确性。研究通过模拟发现，Ising 机执行统计采样的速度比基于软件的方法快几个数量级。这使得可以将 Ising 机应用到超越组合优化的场景，使它们成为机器学习和其他应用的高效工具。

图：（a）模拟 Ising 机通过注入噪声，实现超快速的统计采样；（b）自旋振幅和 Ising 能量的演化；（c）实验设置。

关于Complexity Express

Complex World, Simple Rules.

复杂世界，简单规则。

由于学科交叉融合，大量针对复杂系统的研究成果散落在人工智能、统计物理、网络科学、数据科学、计算社会科学、生命科学、认知科学等等不同领域的期刊会议中，缺乏整合。

为了让大家能及时把握复杂系统领域重要的研究进展，我们隆重推出「Complexity Express」服务，汇总复杂系统相关的最新顶刊论文。

Complexity Express 是什么？

Complexity Express 每天爬取复杂系统领域最新发表的顶刊论文，每周通过“集智斑图”服务号汇总推送。

进入 Complexity Express 页面即可随时查看顶刊论文更新，你也可以通过微信接收研究更新推送和一周汇总。

Complexity Express 为谁服务？

如果你是复杂系统领域的研究者，可获得重要论文上线通知，每周获取最新顶刊论文汇总。
如果你是复杂系统领域的学习者，可了解学界关注的前沿问题，把握专业发展脉络。
如果你是传统的生命科学、社会科学等学科中的研究者/学习者，可以从复杂科学和跨学科研究中获得灵感启发。
如果你是关注前沿研究发现的知识猎手，可获得复杂系统研究对自然和人类世界的最新洞见。

Complexity Express 栏目也是集智俱乐部公众号的主要选题来源，诚挚邀请你订阅，与我们信息同步。

Complexity Express 论文从哪里来？

考虑复杂系统研究往往属于跨学科工作，我们主要抓取综合类和泛物理类/计算机类的顶级期刊，从每周新发表的数百篇论文中精选出与复杂系统相关的论文。

Complexity Express 参考影响因子和学者口碑，选择了如下期刊，每日爬取其论文更新：

Nature
Science
PNAS
Nature Communications
Science Advances
Physics Reports
Physical Review Letters
Physical Review X
Nature Physics
Nature Human Behaviour
Nature Machine Intelligence
Review of Modern Physics
Nature Review Physics
Nature Computational Science
National Science Review
更多期刊持续增补中，欢迎推荐你认为重要的期刊！

如果你在 Complexity Express 中发现了感兴趣的论文，请立刻“点赞”！每周最高赞的论文，集智编辑部将组织专业解读~

Complexity Express 追踪哪些领域？

我们力求兼顾热点追踪与领域覆盖，目前筛选的论文主要集中在如下与复杂性关系密切的领域：

复杂系统基本理论
复杂网络方法及应用
图网络与深度学习
计算机建模与仿真
统计物理与复杂系统
量子计算与量子信息
生态系统、进化、生物物理等
系统生物学与合成生物学
计算神经科学与认知神经科学
计算社会科学与社会经济复杂系统
城市科学与人类行为
科学学
计算流行病学
以及一些领域小众，但有趣的工作

由于复杂性研究领域横跨多个学科，研究论文散落在不同的期刊上，很难不重不漏地把握最新工作。针对复杂性领域的论文筛选，我们专门设计了算法。经过数月的训练迭代优化，目前对上述领域爬取准确率达到90%以上。

将来我们还会根据你的具体研究领域，推出研究分类与个性化的订阅服务，敬请期待！

由于复杂性领域涉及的论文关键词和研究问题纷繁复杂，所以算法难免有不成熟的地方，如果你发现我们有漏掉的重要论文，或者爬到了领域有偏差的论文，欢迎联系我们（小助手微信：swarmaAI），帮助我们持续优化算法。

如果你对科学学、计算术语学等感兴趣并有代码能力，欢迎报名成为集智算法志愿者/实习生（具体请邮件联系算法组负责人huqiao@swarma.org）。

如果你对复杂科学及相关跨学科研究有长期兴趣，并乐于解读分享，欢迎加入集智作者团队（具体请邮件联系编辑部负责人liupeiyuan@swarma.org）。

更多论文

更多复杂性顶刊论文，请到Complexity Express页面查看。订阅即可每周获取更新提醒。

点击“阅读原文”，追踪复杂科学顶刊论文