motif局部社区发现——MAPPR算法

导语

局部图聚类方法旨在通过探索图的小区域来找到节点集群，优于传统的全局图聚类方法，但当前的局部图聚类方法无法解释高阶结构，也不能有效地处理有向网络。本文介绍了一类基于网络模体（motif）捕获高阶网络信息的局部图聚类方法：近似个性化PageRank (MAPPR) 算法，该算法能找到包含具有最小模体电导（motif conductance）的种子节点集。在合成网络和真实网络中对社区检测任务进行的实验验证表明，近似个性化PageRank算法优于当前基于边缘的个性化PageRank算法。

无知影 | 作者

邓一雪 | 编辑

社区发现一直是图数据挖掘的重要阵地之一，然而现有算法大多是将全图为输入，这对处理超大型网络而言十分不利。事实上，在相当多的场景下，例如非法团伙检测任务，我们只需要对非法节点所在社区进行检测即可，而局部社区发现正是通过探索图的一个小区域来发现社区，这种方法能极大提高计算速度。本文介绍一篇来自斯坦福大牛Jure Leskovec团队发表于2017年KDD上的论文，文中提出的方法能够融入更高阶的网络信息来解决局部社区发现问题：

论文题目：

Local Higher-Order Graph Clustering

论文地址：

https://dl.acm.org/doi/10.1145/3097983.3098069

（论文的相关代码可以在斯坦福的SNAP中找到）

论文贡献

使用motif计算近似PPR向量即MAPPR，改进了局部社区发现算法
提出了局部社区发现的选种策略
在实验中对比了其他算法，证明了MAPPR局部社区发现的有效性

相关背景知识

cut、volume和conductance

cut：对于某个节点集合S而言，仅有一个端点S内的边的数量称为S的cut (译为“割”)，可以表示为cut(S)
volume：对于某个节点集合S而言，有端点在S内的边的数量称为S的volume (译为“容量“)，可以表示为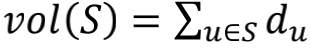， d_u 指的是节点u的度
conductance：对于某个节点集合S而言，它的conductance (译作“电导率”) 可以表示为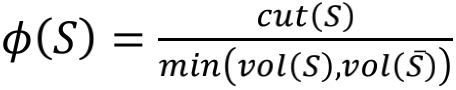：；在局部社区发现算法中，我们通常要求局部社区需要有比较小的conductance

举个栗子：对于下图中红色圈起来节点集合S，cut(S)=4, volume(S)=20, conductance(S)=4/20

motif、motif cut、motif volume和motif conductance

motif：在图中重复出现的，具有显著意义的连接模式（其实就是图中反复出现的小型子图，类似DNA的某些基因片段），比如下面这三种：

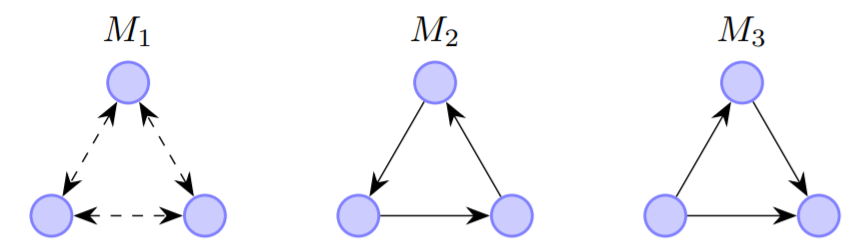
这些都叫三角模体 (motif)

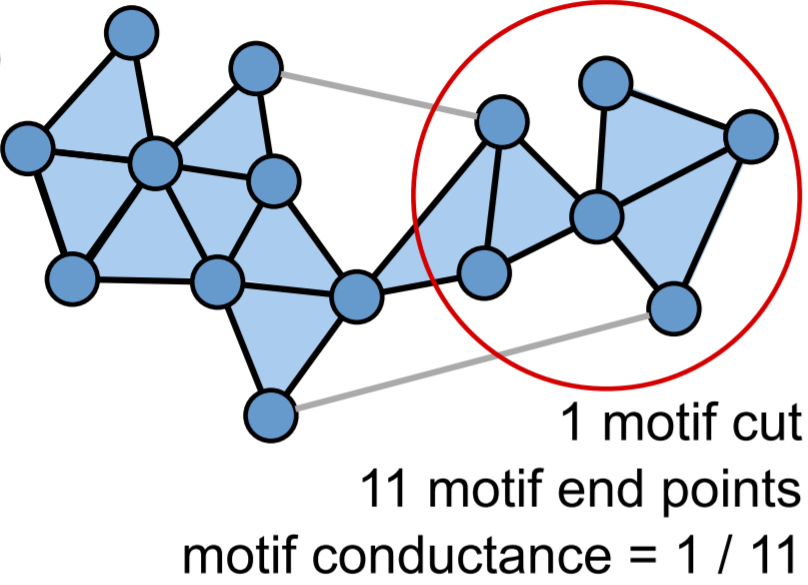
motif cut：对于某个节点集合S而言，motif cut指仅有部分端点在S中的motif的数量，可以表示为cut_M(S)
motif volume：对于某个节点集合S而言，motif volume指S中所占的motif端点数量，可以表示为vol_M(S)
motif conductance：对于某个节点集合S而言，它的conductance (译作“电导率”) 可以表示为：

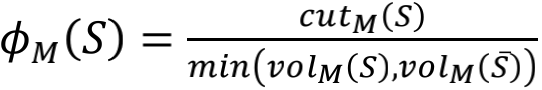
举个栗子：对于下图中红色圈起来节点集合S，cut_M(S)=1, volume_M(S)=11, conductance_M(S)=1/11

局部社区发现：MAPPR算法

在之前的ACL算法中我们曾介绍过Personalized PageRank和PPR向量，简单来说PPR向量是对于网络中某个节点而言，其他节点的重要性，想要利用PPR向量进行局部社区发现只需sweep过程 (sweep procedure)，该过程有以下三个步骤：

1. 既然PPR能够表示网络中的其他节点对某个节点n的重要性，那么我们就可以按照重要性从高到低的顺序，依次尝试将其他节点拉入n所在的局部社区。

2. 在此过程中如果某个节点的加入使得局部社区conductance减小，我们就将它正式拉进这个局部社区。

3. 达到收敛条件后，局部社区将划分完成。

在本文中，我们只需要对上述过程进行简单的改进即可：

1. 构建一个加权图W，其邻接矩阵元素W_ij表示为节点i和j共同作为motif端点的次数

2. 在这个加权图上计算MAPPR向量

3. 将第2步得到的PPR向量用于sweep过程进行局部社区发现

改进后的算法框架伪代码可以表示为：

改进后的sweep过程

α是一个超参数，文中建议设置为0.98
ε是一个阈值，文中建议，其中

MAPPR向量的计算可以表示如下，相对于ACL算法而言，本文仅仅是在push部分做了修改：

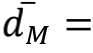
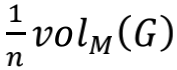
如何找到适合局部社区发现的种子节点：Local minima

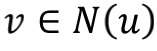本文的另一个亮点是提出了局部社区发现的选种策略，事实上，选择一系列“好种子”能大大增强算法的效果。作者采用了一系列定理和推导来证明选种策略（证明过程太长这里我们直接看结论，有兴趣的朋友可以看原文）：

“好种子”一定是图中的Local minima

注：对于某个节点u和u的邻居节点而言，若，则称节点u是Local minima

实验

Planted partition model和LFR model是图的生成模型，该类模型可以生成具有社区结构的网络，其参数μ控制了社区的重叠程度，μ越大，图中的社区重叠程度越高，进而社区越难被检测出来。下图中蓝色曲线表示MAPPR局部社区发现，红色曲线表示ACL局部社区发现算法，对比可以看出MAPPR局部社区发现能够在更复杂的图中发掘出社区结构。

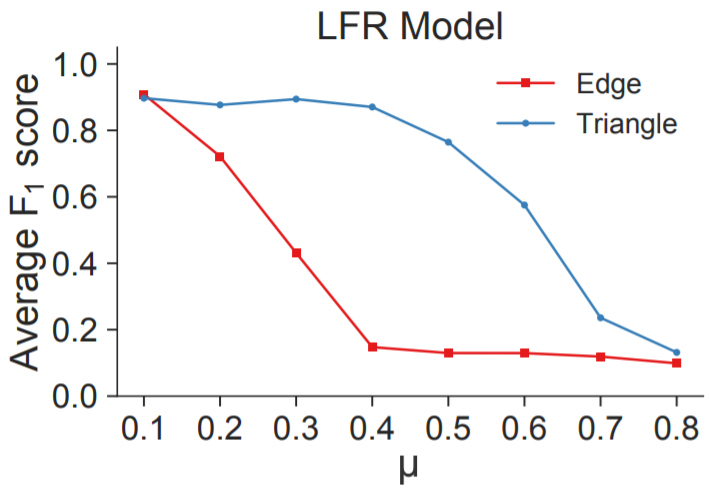
接下来的实验在几个真实的数据集上进行，作者首先使用无向motif的MAPPR局部社区发现进行对比实验，可以看到算法在绝大多数数据集上都取得了提升

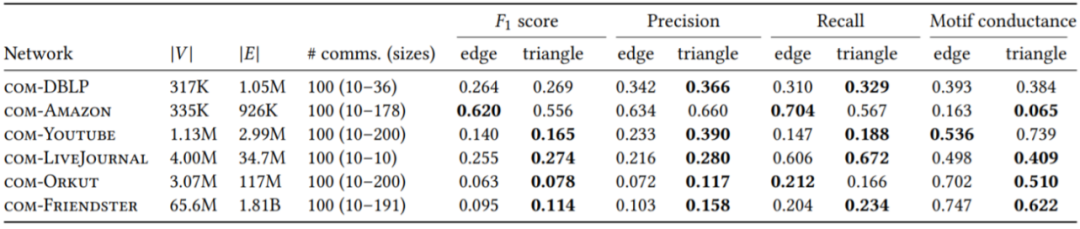
随后作者也使用了有向motif的MAPPR局部社区发现进行对比实验 (即三种不同的三角有向motif: M₁, M₂, M₃)，可以看到该算法有比较显著的优势

作者也绘制了使用不同方法得到局部社区的motif conductance，可以看到使用了MAPPR局部社区发现得到的局部社区的conductance都比较小（尤其是M₃即紫色conductance分布）

以上就是本文的所有内容啦~

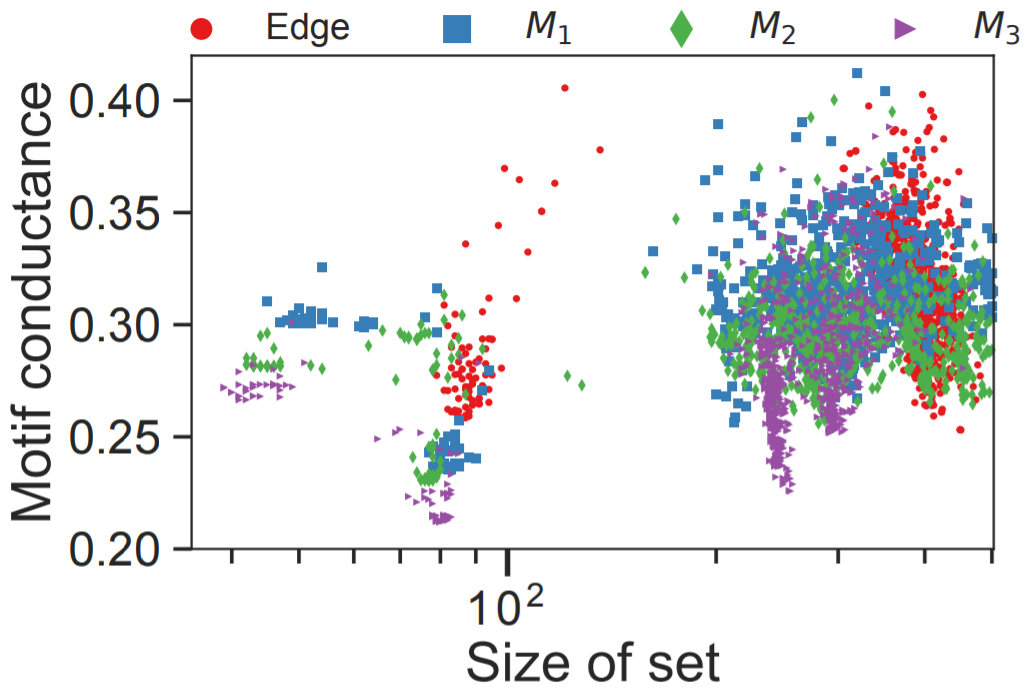
高阶网络读书会启动

随着对现实世界探索的不断深入，人们发现在许多真实的复杂系统中，组成系统的个体之间不仅存在二元交互关系，也广泛存在多个体同时（或以特定顺序）进行交互，即高阶交互现象。为此，研究人员分别发展出了基于超图、单纯复形、依赖关系等的网络高阶表示模型，为复杂网络分析和研究提供了新的思路。为了促进此领域的交流与合作，我们发起了【高阶网络读书会】。

集智俱乐部读书会是面向广大科研工作者的系列论文研读活动，其目的是共同深入学习探讨某个科学议题，激发科研灵感，促进科研合作。【高阶网络读书会】由电子科技大学吕琳媛老师、任晓龙老师及中国地质大学（北京）管青老师联合发起，每周分享时间为每周四 19:30-21:30 进行，预计持续 10-12 周。这其间，我们将围绕高阶交互网络的基本概念、模型、方法与应用等研究进行研讨，本次读书会分享会按照「基础理论」+「深入理论」+「案例研讨」的模式展开。