1. T. Vicsek and A. Zafeiris, “Collective motion,” Phys. Rep. 517, 71–140 (2012). https://doi.org/10.1016/j.physrep.2012.03.004,
2. P. A. Westley, A. M. Berdahl, C. J. Torney, and D. Biro, Collective movement in ecology: From emerging technologies to conservation and management,” Phil. Trans. R. Soc. B 373, 20170004 (2018). https://doi.org/10.1098/rstb.2017.0004,
3. P. W. Anderson, “More is different,” Science 177, 393–396 (1972). https://doi.org/10.1126/science.177.4047.393,
4. L. Conradt and T. J. Roper, “Consensus decision making in animals,” Trends. Ecol. Evol. (Amst.) 20, 449–456 (2005). https://doi.org/10.1016/j.tree.2005.05.008,
5. A. M. Berdahl, A. B. Kao, A. Flack, P. A. Westley, E. A. Codling, I. D. Couzin, A. I. Dell, and D. Biro, “Collective animal navigation and migratory culture: From theoretical models to empirical evidence,” Philos. Trans. R. Soc. B 373, 20170009 (2018). https://doi.org/10.1098/rstb.2017.0009,
6. B. Helm, T. Piersma, and H. Van der Jeugd, “Sociable schedules: Interplay between avian seasonal and social behaviour,” Anim. Behav. 72, 245–262 (2006). https://doi.org/10.1016/j.anbehav.2005.12.007,
7. A. Berdahl, P. A. Westley, and T. P. Quinn, “Social interactions shape the timing of spawning migrations in an anadromous fish,” Anim. Behav. 126, 221–229 (2017). https://doi.org/10.1016/j.anbehav.2017.01.020,
8. L. Conradt and T. J. Roper, “Group decision-making in animals,” Nature 421, 155 (2003). https://doi.org/10.1038/nature01294,
9. I. D. Couzin, J. Krause, N. R. Franks, and S. A. Levin, “Effective leadership and decision-making in animal groups on the move,” Nature 433, 513–516 (2005). https://doi.org/10.1038/nature03236,
10. M. d. M. Delgado, M. Miranda, S. J. Alvarez, E. Gurarie, W. F. Fagan, V. Penteriani, A. di Virgilio, and J. M. Morales, “The importance of individual variation in the dynamics of animal collective movements,” Philos. Trans. R. Soc. B 373, 20170008 (2018). https://doi.org/10.1098/rstb.2017.0008,
11. L. F. Hughey, A. M. Hein, A. Strandburg-Peshkin, and F. H. Jensen, “Challenges and solutions for studying collective animal behaviour in the wild,” Philos. Trans. R. Soc. B 373, 20170005 (2018). https://doi.org/10.1098/rstb.2017.0005,
12. A. Strandburg-Peshkin, D. Papageorgiou, M. C. Crofoot, and D. R. Farine, “Inferring influence and leadership in moving animal groups,” Philos. Trans. R. Soc. B 373, 20170006 (2018). https://doi.org/10.1098/rstb.2017.0006,
13. J. E. Smith, S. Gavrilets, M. B. Mulder, P. L. Hooper, C. El Mouden, D. Nettle, C. Hauert, K. Hill, S. Perry, A. E. Pusey, M. van Vugt, and E. A. Smith, “Leadership in mammalian societies: Emergence, distribution, power, and payoff,” Trends Ecol. Evol. (Amst.) 31, 54–66 (2016). https://doi.org/10.1016/j.tree.2015.09.013,
14. J. S. Lewis, D. Wartzok, and M. R. Heithaus, “Highly dynamic fission–fusion species can exhibit leadership when traveling,” Behav. Ecol. Sociobiol. 65, 1061–1069 (2011). https://doi.org/10.1007/s00265-010-1113-y,
15. L. J. Brent, D. W. Franks, E. A. Foster, K. C. Balcomb, M. A. Cant, and D. P. Croft, “Ecological knowledge, leadership, and the evolution of menopause in killer whales,” Curr. Biol. 25, 746–750 (2015). https://doi.org/10.1016/j.cub.2015.01.037,
16. D. M. Jacoby, Y. P. Papastamatiou, and R. Freeman, “Inferring animal social networks and leadership: Applications for passive monitoring arrays,” J. R. Soc. Interface 13, 20160676 (2016). https://doi.org/10.1098/rsif.2016.0676,
17. A. Strandburg-Peshkin, D. R. Farine, I. D. Couzin, and M. C. Crofoot, “Shared decision-making drives collective movement in wild baboons,” Science 348, 1358–1361 (2015). https://doi.org/10.1126/science.aaa5099,
18. J.-B. Leca, N. Gunst, B. Thierry, and O. Petit, “Distributed leadership in semifree-ranging white-faced capuchin monkeys,” Anim. Behav. 66, 1045–1052 (2003). https://doi.org/10.1006/anbe.2003.2276,
19. M. Nagy, Z. Akos, D. Biro, and T. Vicsek, “Hierarchical group dynamics in pigeon flocks,” Nature 464, 890–893 (2010). https://doi.org/10.1038/nature08891,
20. Z. Ákos, R. Beck, M. Nagy, T. Vicsek, and E. Kubinyi, “Leadership and path characteristics during walks are linked to dominance order and individual traits in dogs,” PLoS Comput. Biol. 10, e1003446 (2014). https://doi.org/10.1371/journal.pcbi.1003446,
21. L. Jiang, L. Giuggioli, A. Perna, R. Escobedo, V. Lecheval, C. Sire, Z. Han, and G. Theraulaz, “Identifying influential neighbors in animal flocking,” PLoS Comput. Biol. 13, e1005902 (2017). https://doi.org/10.1371/journal.pcbi.1005822,
22. I. Watts, M. Nagy, R. I. Holbrook, D. Biro, and T. B. de Perera, “Validating two-dimensional leadership models on three-dimensionally structured fish schools,” R. Soc. Open. Sci. 4, 160804 (2017). https://doi.org/10.1098/rsos.160804,
23. H. Ye, E. R. Deyle, L. J. Gilarranz, and G. Sugihara, “Distinguishing time-delayed causal interactions using convergent cross mapping,” Sci. Rep. 5 (2015). https://doi.org/10.1038/srep14750,
24. W. M. Lord, J. Sun, N. T. Ouellette, and E. M. Bollt, “Inference of causal information flow in collective animal behavior,” IEEE Trans. Mol. Biol. Multi-Scale Commun. 2, 107–116 (2016). https://doi.org/10.1109/TMBMC.2016.2632099,
25. S. Butail, V. Mwaffo, and M. Porfiri, “Model-free information-theoretic approach to infer leadership in pairs of zebrafish,” Phys. Rev. E 93, 042411 (2016). https://doi.org/10.1103/PhysRevE.93.042411,
26. J. Sun, D. Taylor, and E. M. Bollt, “Causal network inference by optimal causation entropy,” SIAM. J. Appl. Dyn. Syst. 14, 73–106 (2015). https://doi.org/10.1137/140956166,
27. N. Thorpe, N. Hakongak, S. Eyegetok, and the Kitikmeot Elders, Thunder on the Tundra: Inuit Qaujimajatuqangit of the Bathurst Caribou (Generation Printing, Vancouver, 2001).
28. P. S. Barboza and K. L. Parker, “Allocating protein to reproduction in arctic reindeer and caribou,” Physiol. Biochem. Zool. 81, 835–855 (2008). https://doi.org/10.1086/590414,
29. L. Conradt, J. Krause, I. D. Couzin, and T. J. Roper, “Leading according to need in self-organizing groups,” Am. Nat. 173, 304–312 (2009). https://doi.org/10.1086/596532,
30. C. J. Torney, M. Lamont, L. Debell, R. J. Angohiatok, L.-M. Leclerc, and A. M. Berdahl, “Inferring the rules of social interaction in migrating caribou,” Philos. Trans. R. Soc. B 373, 20170385 (2018). https://doi.org/10.1098/rstb.2017.0385,
31. T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen, and O. Shochet, “Novel type of phase transition in a system of self-driven particles,” Phys. Rev. Lett. 75, 1226 (1995). https://doi.org/10.1103/PhysRevLett.75.1226,
32. E. M. Bollt and N. Santitissadeekorn, Applied and Computational Measurable Dynamics (SIAM, 2013).
33. R. G. James, N. Barnett, and J. P. Crutchfield, “Information flows? A critique of transfer entropies,” Phys. Rev. Lett. 116, 238701 (2016). https://doi.org/10.1103/PhysRevLett.116.238701,
34. J. C. Flack and D. C. Krakauer, “Encoding power in communication networks,” Am. Nat. 168, E87–E102 (2006). https://doi.org/10.1086/506526,
35. E. R. Brush, D. C. Krakauer, and J. C. Flack, “A family of algorithms for computing consensus about node state from network data,” PLoS Comput. Biol. 9, e1003109 (2013). https://doi.org/10.1371/journal.pcbi.1003109,
36. C. De Bacco, D. B. Larremore, and C. Moore, “A physical model for efficient ranking in networks,” arXiv preprint arXiv:1709.09002 (2017).
37. A. Strandburg-Peshkin, C. R. Twomey, N. W. Bode, A. B. Kao, Y. Katz, C. C. Ioannou, S. B. Rosenthal, C. J. Torney, H. S. Wu, S. A. Levin, and I. Couzin, “Visual sensory networks and effective information transfer in animal groups,” Curr. Biol. 23, R709–R711 (2013). https://doi.org/10.1016/j.cub.2013.07.059,
38. S. G. Reebs, “Can a minority of informed leaders determine the foraging movements of a fish shoal?” Anim. Behav. 59, 403–409 (2000). https://doi.org/10.1006/anbe.1999.1314,
39. T. Mueller, R. B. O’Hara, S. J. Converse, R. P. Urbanek, and W. F. Fagan, “Social learning of migratory performance,” Science 341, 999–1002 (2013). https://doi.org/10.1126/science.1237139,
40. K. M. Schultz, K. M. Passino, and T. D. Seeley, “The mechanism of flight guidance in honeybee swarms: Subtle guides or streaker bees?” J. Exp. Biol. 211, 3287–3295 (2008). https://doi.org/10.1242/jeb.018994,
41. C. J. Torney, A. Berdahl, and I. D. Couzin, “Signalling and the evolution of cooperative foraging in dynamic environments,” PLoS Comput. Biol. 7, e1002194 (2011). https://doi.org/10.1371/journal.pcbi.1002194,
42. B. Pettit, Z. Ákos, T. Vicsek, and D. Biro, “Speed determines leadership and leadership determines learning during pigeon flocking,” Curr. Biol. 25, 3132–3137 (2015). https://doi.org/10.1016/j.cub.2015.10.044,
43. K. J. Stewart and A. H. Harcourt, “Gorillas’ vocalizations during rest periods: Signals of impending departure? ”Behaviour 130, 29–40 (1994). https://doi.org/10.1163/156853994X00127,
44. D. Fossey, “Vocalizations of the mountain gorilla (Gorilla gorilla beringei),” Anim. Behav. 20, 36–53 (1972). https://doi.org/10.1016/S0003-3472(72)80171-4,
45. J. M. Smith and D. Harper, Animal Signals (Oxford University Press, 2003).
46. J. M. Black, “Preflight signalling in swans: A mechanism for group cohesion and flock formation,” Ethology 79, 143–157 (1988). https://doi.org/10.1111/j.1439-0310.1988.tb00707.x,
47. A. J. King, C. M. Douglas, E. Huchard, N. J. Isaac, and G. Cowlishaw, “Dominance and affiliation mediate despotism in a social primate,” Curr. Biol. 18, 1833–1838 (2008). https://doi.org/10.1016/j.cub.2008.10.048,
48. K. Payne, Sources of Social Complexity in the Three Elephant Species (Harvard University Press, 2003).
49. R. O. Peterson, A. K. Jacobs, T. D. Drummer, L. D. Mech, and D. W. Smith, “Leadership behavior in relation to dominance and reproductive status in gray wolves, canis lupus,” Can. J. Zool. 80, 1405–1412 (2002). https://doi.org/10.1139/z02-124,
50. D. Lusseau and L. Conradt, “The emergence of unshared consensus decisions in bottlenose dolphins,” Behav. Ecol. Sociobiol. 63, 1067–1077 (2009). https://doi.org/10.1007/s00265-009-0740-7,
51. J. C. Flack, M. Girvan, F. B. De Waal, and D. C. Krakauer, “Policing stabilizes construction of social niches in primates,” Nature 439, 426 (2006). https://doi.org/10.1038/nature04326,
52. S. B. Rosenthal, C. R. Twomey, A. T. Hartnett, H. S. Wu, and I. D. Couzin, “Revealing the hidden networks of interaction in mobile animal groups allows prediction of complex behavioral contagion,” Proc. Natl. Acad. Sci. 112, 4690–4695 (2015). https://doi.org/10.1073/pnas.1420068112,
53. K. N. Laland and K. Williams, “Shoaling generates social learning of foraging information in guppies,” Anim. Behav. 53, 1161–1169 (1997). https://doi.org/10.1006/anbe.1996.0318,
54. A. Flack, B. Pettit, R. Freeman, T. Guilford, and D. Biro, “What are leaders made of? The role of individual experience in determining leader–follower relations in homing pigeons,” Anim. Behav. 83, 703–709 (2012). https://doi.org/10.1016/j.anbehav.2011.12.018,
55. M. Nagy, I. D. Couzin, W. Fiedler, M. Wikelski, and A. Flack, “Synchronization, coordination and collective sensing during thermalling flight of freely migrating white storks,” Philos. Trans. R. Soc. B 373, 20170011 (2018). https://doi.org/10.1098/rstb.2017.0011,
56. A. Berdahl, C. J. Torney, C. C. Ioannou, J. J. Faria, and I. D. Couzin, “Emergent sensing of complex environments by mobile animal groups,” Science 339, 574–576 (2013). https://doi.org/10.1126/science.1225883,
57. C. W. Reynolds, “Flocks, herds and schools: A distributed behavioral model,” in ACM SIGGRAPH Computer Graphics (ACM, 1987), 21, pp. 25–34.
58. I. D. Couzin, J. Krause, R. James, G. D. Ruxton, and N. R. Franks, “Collective memory and spatial sorting in animal groups,” J. Theor. Biol. 218, 1–11 (2002). https://doi.org/10.1006/jtbi.2002.3065,
59. N. W. Bode, A. J. Wood, and D. W. Franks, “The impact of social networks on animal collective motion,” Anim. Behav. 82, 29–38 (2011). https://doi.org/10.1016/j.anbehav.2011.04.011,
60. C. R. Brown, M. B. Brown, and M. L. Shaffer, “Food-sharing signals among socially foraging cliff swallows,” Anim. Behav. 42, 551–564 (1991). https://doi.org/10.1016/S0003-3472(05)80239-8,
61. T. Schreiber, “Measuring information transfer,” Phys. Rev. Lett. 85, 461–4 (2000). https://doi.org/10.1103/PhysRevLett.85.461,
62. D. Darmon, E. Omodei, and J. Garland, “Followers are not enough: A multifaceted approach to community detection in online social networks,” PLoS ONE 10, e0134860 (2015). https://doi.org/10.1371/journal.pone.0134860,
63. E. M. Bollt, “Synchronization as a process of sharing and transferring information,” Int. J. Bifurcat. Chaos 22, 1250261 (2012). https://doi.org/10.1142/S0218127412502616,
64. J. Sun and E. M. Bollt, “Causation entropy identifies indirect influences, dominance of neighbors and anticipatory couplings,” Phys. D: Nonlin. Phenom. 267, 49–57 (2014). https://doi.org/10.1016/j.physd.2013.07.001,
65. C. Cafaro, W. M. Lord, J. Sun, and E. M. Bollt, “Causation entropy from symbolic representations of dynamical systems,” Chaos: Interdiscip. J. Nonlin. Sci. 25, 043106 (2015). https://doi.org/10.1063/1.4916902, Scitation, ISI
66. C. W. Granger, “Testing for causality: A personal viewpoint,” J. Econ. Dyn. Control 2, 329–352 (1980). https://doi.org/10.1016/0165-1889(80)90069-X,
67. J. Sun, C. Cafaro, and E. M. Bollt, “Identifying the coupling structure in complex systems through the optimal causation entropy principle,” Entropy 16, 3416–3433 (2014). https://doi.org/10.3390/e16063416,
68. B. Russell, Mysticism and Logic (New Statesman, 1913).
69. B. Russell, Human Knowledge: Its Scope and Its Limits (Simon & Schuster, New York, 1948).
70. J. Bigelow and R. Pargetter, “Metaphysics of causation,” Erkenntnis 33, 89–119 (1990). https://doi.org/10.1007/BF00634553,
71. J. Pearl and T. S. Verma, “A theory of inferred causation,” in Studies in Logic and the Foundations of Mathematics (Elsevier, 1995), Vol. 134, pp. 789–811.
72. J. Pearl, “Bayesian networks” (2011), available at https://escholarship.org/uc/item/53n4f34m.
73. J. Pearl, “The structural theory of causation,” in Causality in the Sciences (Clarendon Press, Oxford, 2011), pp. 697–727.
74. B. Skyrms and W. L. Harper, Causation, Chance and Credence: Proceedings of the Irvine Conference on Probability and Causation (Springer Science & Business Media, 2012), Vol. 1.
75. D. A. Freedman, “Linear statistical models for causation: A critical review,” Encyclopedia Stat. Behav. Sci. (2005). https://doi.org/10.1002/0470013192.bsa598,
76. L. Barnett, A. B. Barrett, and A. K. Seth, “Granger causality and transfer entropy are equivalent for gaussian variables,” Phys. Rev. Lett. 103, 238701 (2009). https://doi.org/10.1103/PhysRevLett.103.238701,



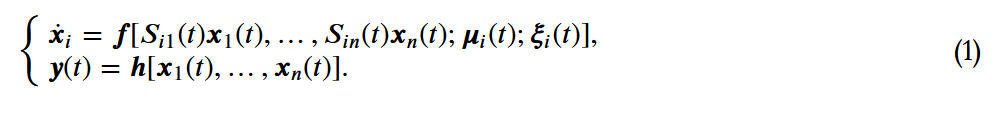
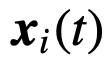 代表第i个个体在时间
代表第i个个体在时间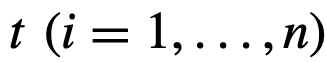 的状态。
的状态。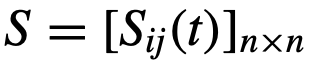 是编码交互结构的网络的(与时间相关的)邻接矩阵(也称为社会性矩阵),其中如果j有可能(直接)影响i的状态,则
是编码交互结构的网络的(与时间相关的)邻接矩阵(也称为社会性矩阵),其中如果j有可能(直接)影响i的状态,则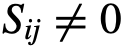 。此外,
。此外, 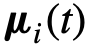 表示与i相关的参数(向量),
表示与i相关的参数(向量),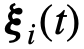 是噪声。这里的参数可以是描述群体中个体异质性的任何东西。例如,在Viscek模型中[31],参数
是噪声。这里的参数可以是描述群体中个体异质性的任何东西。例如,在Viscek模型中[31],参数 可以表示个体的偏好方向,也可以用来表示个体之间可能存在的速度差异,或者通过给每个个体关联一个参数向量来表示两者。函数f模拟每个个体的动力学如何取决于他们自己的状态和参数、网络中其他个体的状态以及噪声。最后,群体的状态
可以表示个体的偏好方向,也可以用来表示个体之间可能存在的速度差异,或者通过给每个个体关联一个参数向量来表示两者。函数f模拟每个个体的动力学如何取决于他们自己的状态和参数、网络中其他个体的状态以及噪声。最后,群体的状态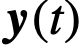 是由个体的状态通过函数h决定的;例如,取
是由个体的状态通过函数h决定的;例如,取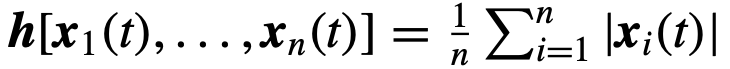 将群体状态定义为个体状态的平均值。
将群体状态定义为个体状态的平均值。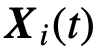 和
和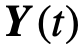 。从这个角度来看,群体变量和变量之间的关系被编码为条件分布函数 :
。从这个角度来看,群体变量和变量之间的关系被编码为条件分布函数 :
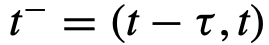 表示系统的时间历史,考虑到
表示系统的时间历史,考虑到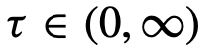 的时滞。
的时滞。

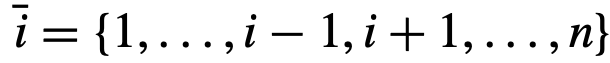 。正如James等人最近建议的那样[33],公式(4)可能无法完全反映影响;因此,在以这种方式量化净影响时,应该注意。
。正如James等人最近建议的那样[33],公式(4)可能无法完全反映影响;因此,在以这种方式量化净影响时,应该注意。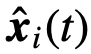 来表示关于
来表示关于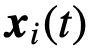 的观察状态,同样地,
的观察状态,同样地,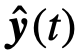 表示关于
表示关于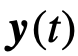 的观察状态。我们在一个有限的时间窗口上表示观察结果,产生观察数据:
的观察状态。我们在一个有限的时间窗口上表示观察结果,产生观察数据:
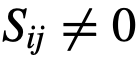 ,其中“领导能力”由特定的社会来定义。
,其中“领导能力”由特定的社会来定义。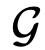 是与社会性矩阵S相关的有向图,其中如果
是与社会性矩阵S相关的有向图,其中如果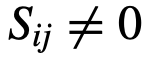 ,则存在一条从j到i的边。对于每个节点
,则存在一条从j到i的边。对于每个节点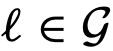 ,将节点
,将节点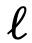 的可达性集合表示为
的可达性集合表示为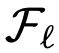 。特别是,如果在
。特别是,如果在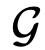 中存在一条从
中存在一条从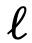 到k的有向路径,则节点k就是
到k的有向路径,则节点k就是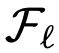 的成员。如果
的成员。如果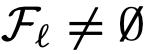 ,那么
,那么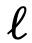 就被定义为具有结构领导能力。我们将具有非零的结构性领导能力(在社会性矩阵上有一个非空的可达性集合)的个体集合定义为L。当然,一个个体作为结构性领导的程度存在于一个连续体上。量化这种领导力的强度是一项高度非琐碎的、可能是特定系统的任务(例如,参考文献[34-36])。然而,首先,在社会性矩阵中,下游个体多而上游个体少的个体将倾向于发挥更强的领导作用,或者至少有潜力这样做。
就被定义为具有结构领导能力。我们将具有非零的结构性领导能力(在社会性矩阵上有一个非空的可达性集合)的个体集合定义为L。当然,一个个体作为结构性领导的程度存在于一个连续体上。量化这种领导力的强度是一项高度非琐碎的、可能是特定系统的任务(例如,参考文献[34-36])。然而,首先,在社会性矩阵中,下游个体多而上游个体少的个体将倾向于发挥更强的领导作用,或者至少有潜力这样做。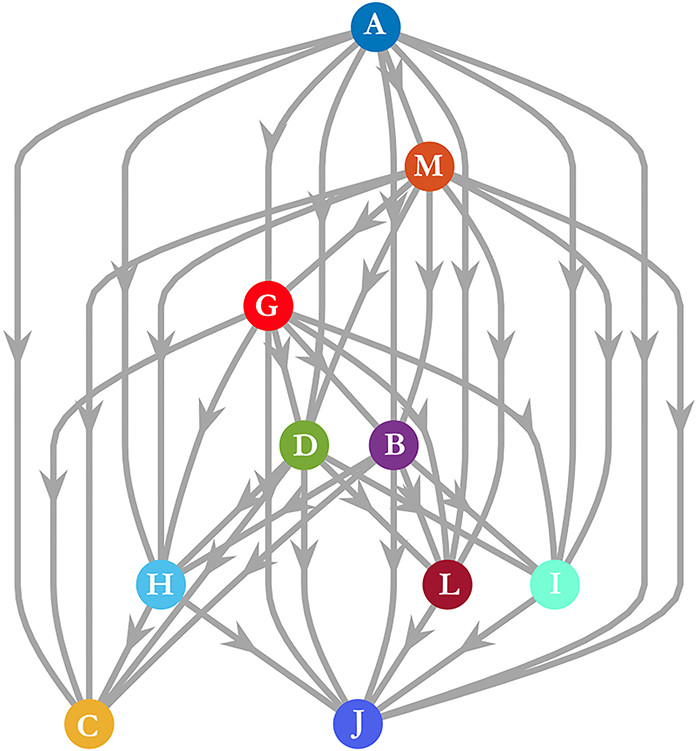
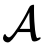 是一组目标状态,那么,如果i对群体的净影响[见公式(4)]非零,则个体i是一个目标驱动的领导者(就
是一组目标状态,那么,如果i对群体的净影响[见公式(4)]非零,则个体i是一个目标驱动的领导者(就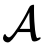 而言)。
而言)。
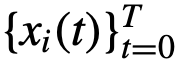 表示。
表示。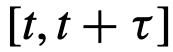 内被确定为领导者,我们就把它归为短暂的,其中
内被确定为领导者,我们就把它归为短暂的,其中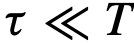 。参考文献[12]中提出了一个类似的时间领导力量表,其范围从可变到一致,但试图捕捉相同的概念。
。参考文献[12]中提出了一个类似的时间领导力量表,其范围从可变到一致,但试图捕捉相同的概念。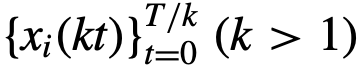 (k>1)来量化领导力。如果一个领导者只在粗粒度的基础上行动,那么他们可能不会在小的𝑘时作为领导者,但随后可能在一些较大的k时作为领导者。与此相反,细粒度的领导者可能在小的k时为领导者。
(k>1)来量化领导力。如果一个领导者只在粗粒度的基础上行动,那么他们可能不会在小的𝑘时作为领导者,但随后可能在一些较大的k时作为领导者。与此相反,细粒度的领导者可能在小的k时为领导者。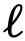 ,其属性为
,其属性为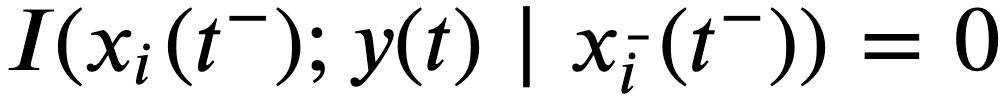 ,即一个不直接影响群体的结构性领导——尽管它有可能。无论采用何种推理方法,这样的潜在领导者总是会被错误地分类。同样地,考虑一个知情型的领导者,只有当他们在已知资源的某个半径范围内时才会领导。假设这个事件只发生在一个很短的时间窗口
,即一个不直接影响群体的结构性领导——尽管它有可能。无论采用何种推理方法,这样的潜在领导者总是会被错误地分类。同样地,考虑一个知情型的领导者,只有当他们在已知资源的某个半径范围内时才会领导。假设这个事件只发生在一个很短的时间窗口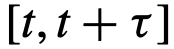 ,其中
,其中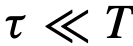 。如果我们只考虑在整个观察窗口中领导的领导者,那么大多数的综合衡量标准将掩盖掉这样一个短暂的领导事件。由于这些原因,通过研究数据集的子样本,仔细考虑一致性,以及通过对数据进行向下取样和重新测试的粒度,人们可能会得到一个更清晰的关于移动的动动物群体中存在的领导的图景。
。如果我们只考虑在整个观察窗口中领导的领导者,那么大多数的综合衡量标准将掩盖掉这样一个短暂的领导事件。由于这些原因,通过研究数据集的子样本,仔细考虑一致性,以及通过对数据进行向下取样和重新测试的粒度,人们可能会得到一个更清晰的关于移动的动动物群体中存在的领导的图景。 是一个网络,如果j有能力领导i,则存在一条从节点j到节点𝑖的有向边,其中领导力可以是结构性的、涌现型或知情型的领导。那么,个体𝑖的可达性就是i在
是一个网络,如果j有能力领导i,则存在一条从节点j到节点𝑖的有向边,其中领导力可以是结构性的、涌现型或知情型的领导。那么,个体𝑖的可达性就是i在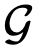 上的可达性集合。
上的可达性集合。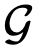 有一个
有一个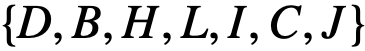 的可达性集合,因此这7个个体都在结构领导者
的可达性集合,因此这7个个体都在结构领导者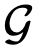 的范围之内。影响力自然是在局部和全局之间的一个连续体。如果一个个体对所有的个体都体现了某种形式的领导力,这将是全局性的影响;如果一个人只领导群体中的一些小子集,那么这个领导者就被认为是局部的。在图2中,个体𝐴具有全局影响力,个体I具有局部影响力。
的范围之内。影响力自然是在局部和全局之间的一个连续体。如果一个个体对所有的个体都体现了某种形式的领导力,这将是全局性的影响;如果一个人只领导群体中的一些小子集,那么这个领导者就被认为是局部的。在图2中,个体𝐴具有全局影响力,个体I具有局部影响力。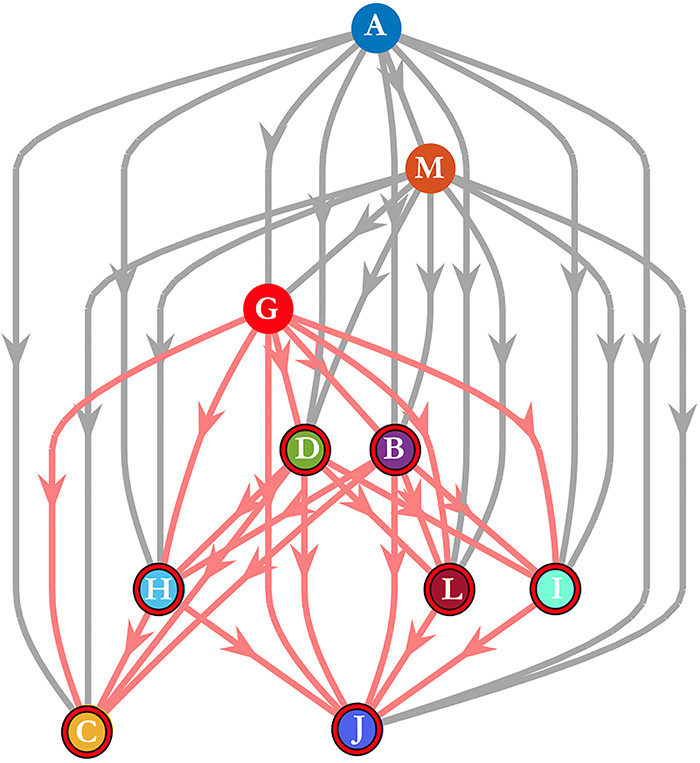
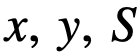 (或是这些的一些混合)定义整个系统的动力学。当系统被观察时,观察到的变量,即
(或是这些的一些混合)定义整个系统的动力学。当系统被观察时,观察到的变量,即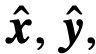 和
和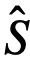 ,可能与真实变量不同。如果一个个体表现出内在变量
,可能与真实变量不同。如果一个个体表现出内在变量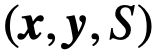 所定义的领导力,但在观察变量
所定义的领导力,但在观察变量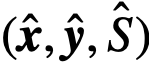 下似乎没有这样做,我们称之为“隐藏的”领导角色。一个没有被隐藏的领导者就被称为可观察的领导者。
下似乎没有这样做,我们称之为“隐藏的”领导角色。一个没有被隐藏的领导者就被称为可观察的领导者。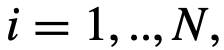 每个时间t,都有一个“集体运动”模型,由向量
每个时间t,都有一个“集体运动”模型,由向量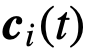 、方向向量
、方向向量 和速度
和速度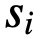 被保持。在每个时间步上,个体𝑖根据三个不同区域的邻居计算出一个期望的方向
被保持。在每个时间步上,个体𝑖根据三个不同区域的邻居计算出一个期望的方向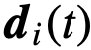 ,如图3所示:
,如图3所示: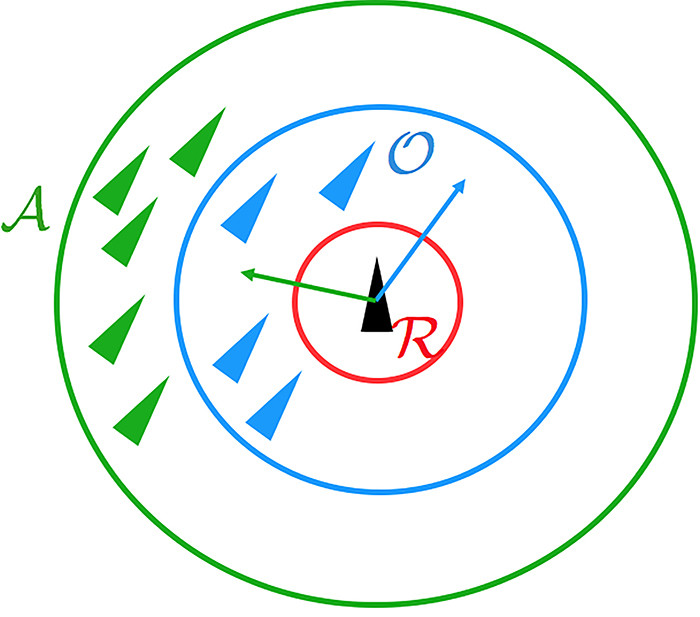
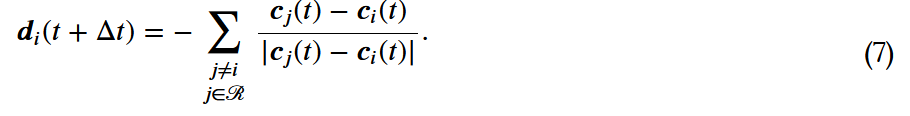
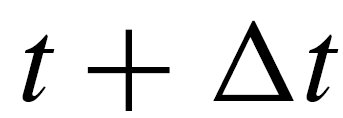 时不会发生碰撞。然而,如果对焦点个体来说,
时不会发生碰撞。然而,如果对焦点个体来说,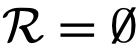 ,那么焦点个体就会试图接近其吸引区的个体,并与它们定向区的个体一起定向。这是通过在时间
,那么焦点个体就会试图接近其吸引区的个体,并与它们定向区的个体一起定向。这是通过在时间 选择一个期望的方向来实现的,方法如下:
选择一个期望的方向来实现的,方法如下: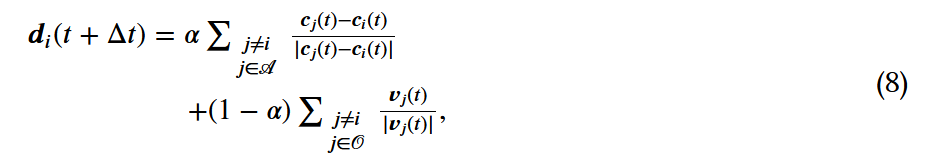
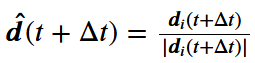
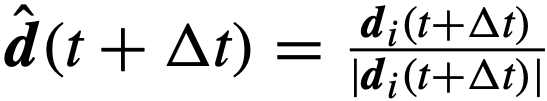 ,将其旋转一个小角度,从以零为中心的圆形包裹的高斯分布中抽取。最后,假设个体在单位时间内的最大转弯速度为θ弧度。因此,如果一个个体的当前方向
,将其旋转一个小角度,从以零为中心的圆形包裹的高斯分布中抽取。最后,假设个体在单位时间内的最大转弯速度为θ弧度。因此,如果一个个体的当前方向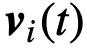 与它在下一时间步长的期望方向之间的差异
与它在下一时间步长的期望方向之间的差异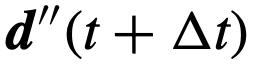 ,小于
,小于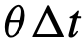 ,那么就达到了期望方向,
,那么就达到了期望方向,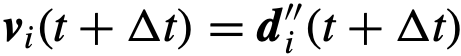 。否则,该个体的方向
。否则,该个体的方向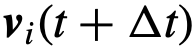 是将
是将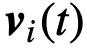 旋转
旋转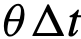 向其期望的方向
向其期望的方向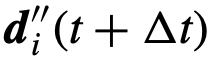 的结果。
的结果。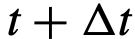 的位置可以通过以下方式计算出来:
的位置可以通过以下方式计算出来: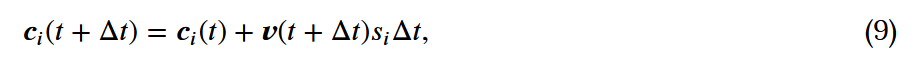
 ,是个体i的速度。
,是个体i的速度。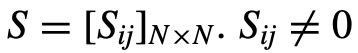 ,如果个体i能被个体j影响。更一般地说,
,如果个体i能被个体j影响。更一般地说,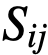 是一个连续值,给出了个体j对个体j的相对影响。为了考虑到这一点,理想方向的计算被修改为对每个邻居相对于
是一个连续值,给出了个体j对个体j的相对影响。为了考虑到这一点,理想方向的计算被修改为对每个邻居相对于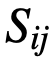 的影响进行加权,而不是对
的影响进行加权,而不是对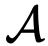 和
和 中的每个人进行等额加权),即:
中的每个人进行等额加权),即: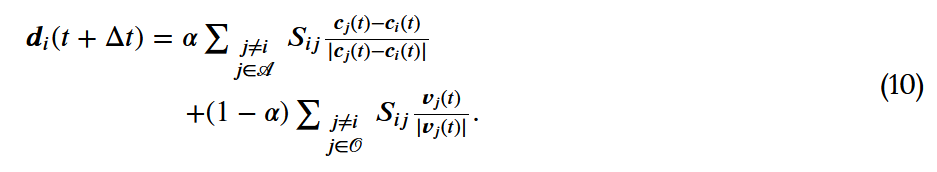
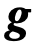 (例如,这个首选方向可以代表一条迁徙路线或一个猎物或已知资源的方向
(例如,这个首选方向可以代表一条迁徙路线或一个猎物或已知资源的方向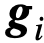 )[9]。不知情的群体成员对
)[9]。不知情的群体成员对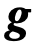 没有了解,可能知道也可能不知道哪些个体是知情的。按照Couzin等人的观点[9],为了将其纳入模型,知情个体在社会互动和他们的首选方向之间用一个加权项𝜔进行平衡。特别是,知情的个体有一个期望的方向
没有了解,可能知道也可能不知道哪些个体是知情的。按照Couzin等人的观点[9],为了将其纳入模型,知情个体在社会互动和他们的首选方向之间用一个加权项𝜔进行平衡。特别是,知情的个体有一个期望的方向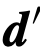 ,由以下公式给出:
,由以下公式给出: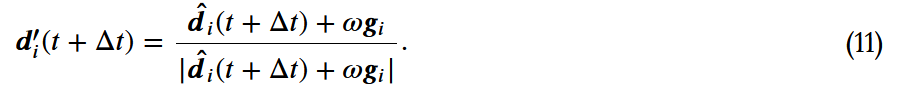
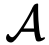 和
和 会有部分盲区,这些盲区中的个体被忽略了。如果这些盲区足够大,个体就会更多地受到他们前面的个体的影响[30]。
会有部分盲区,这些盲区中的个体被忽略了。如果这些盲区足够大,个体就会更多地受到他们前面的个体的影响[30]。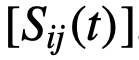 ,
,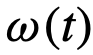 ,以及
,以及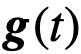 。例如,我们可以通过定义时变的
。例如,我们可以通过定义时变的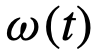 ,在固定的时间间隔内移除或改变首选方向,然后再看推断算法是否能检测到这种变化。
,在固定的时间间隔内移除或改变首选方向,然后再看推断算法是否能检测到这种变化。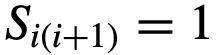 否则为0,
否则为0,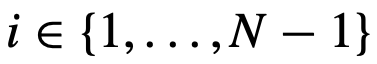 ,并让
,并让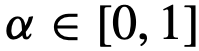 。这描述了一个简单的链式拓扑结构,其中每个个体都有能力对最多一个其它个体进行结构性领导。特别是,每个个体直接定向并吸引到(跟随)群体中最多一个其它个体。然而,需要注意的是,每个个体都要避免与所有其他个体发生碰撞[社会性矩阵适用于公式(10),但不适用于公式(7)]。
。这描述了一个简单的链式拓扑结构,其中每个个体都有能力对最多一个其它个体进行结构性领导。特别是,每个个体直接定向并吸引到(跟随)群体中最多一个其它个体。然而,需要注意的是,每个个体都要避免与所有其他个体发生碰撞[社会性矩阵适用于公式(10),但不适用于公式(7)]。










