复杂系统研究关注简单的部分如何相互作用,在整体层面涌现出复杂现象。这和统计物理通过研究微观粒子的统计行为来解释宏观状态变化具有根本一致性。2021年,Entropy 杂志推出“相变与涌现现象特刊”,聚焦复杂系统的统计物理。特刊共收录6篇相关主题论文,包括2021年诺贝尔物理学奖得主 Giorgio Parisi 关于自旋玻璃相变的工作,以及其他相变与临界现象、伊辛模型、复杂网络等交叉领域研究。
关键词:相变与临界现象,普适性,标度律,伊辛模型,自旋玻璃,统计物理,复杂网络
特刊主题:
Phase Transitions and Emergent Phenomena: How Change Emerges through Basic Probability Models
特刊链接:
https://www.mdpi.com/journal/entropy/special_issues/Probability_Models
特刊信息
特刊论文介绍
1. 真实副本之间的距离变化导致自旋玻璃相变
2. 伊辛自旋玻璃的超标度违反
3. (四)双元格三维伊辛模型
4. 基于伊辛模型的随机块模型的精确恢复
5. 有向 BA 网络上的离散意见动力学模型
6. 网络生成树的普适性和有限尺寸修正
19世纪末,玻尔兹曼(Ludwig Boltzmann)和同时代人开创了统计物理学。该学科的支柱包括“自下而上”的相变理论和临界现象,它建立在如楞次(Wilhelm Lenz)和伊辛(Ernst Ising)在20世纪初的想法和工作的基础上。用霍金的话来说,我们正处于“复杂性的世纪”,关注的问题从支配物质的基本法则,转向一切事物如何相互联系。
尽管伊辛最初的研究并没有得到期望的相变结果,但是随机性加上微观层面的总体简化可以解释宏观层面的状态变化这一想法是开创性的。现在我们知道了维度、相互作用范围、对称性、模型为经典或量子、平衡或非平衡等在理解物理变化中的重要性。
大量的研究涵盖了这类系统的各种变量如何描述日益复杂的系统,但是将概率应用于简化多体系统的基本思想是从社会系统中借鉴来的。近年来,随着“涌现”概念的出现,复杂系统的统计物理重新拥抱了它的跨学科诞生处,补充且拓展了物理学,并为我们对世界的理解做出了贡献。
本期特刊聚焦在微观层面上简单但在宏观层面上复杂的模型。特刊对正面结果和像伊辛这样的负面结果都感兴趣,反思统计物理的发源,同时也欢迎跨学科研究和传统物理学。本刊关注变化这一概念——无论变化发生在何处,简单的事物如何通过非平凡的机制涌现复杂的事物。
Spin Glasses in a Field Show a Phase Transition Varying the Distance among Real Replicas (And How to Exploit It to Find the Critical Line in a Field)
https://www.mdpi.com/1099-4300/22/2/250
这篇论文的作者之一是2021年诺贝尔物理学奖得主 Giorgio Parisi。在物理学中,Parisi 的一项著名工作是自旋玻璃理论中的复本方法(replica method)。复本方法是处理随机相互作用的一个标准技巧。
自旋玻璃理论深刻地揭示了无序体系中的隐藏对称性,Parisi 等人提出了复本间的交叠序参量来表征自旋玻璃的相变。这篇论文讨论了一种过去很少考虑的自旋玻璃模型中的相变,即当两个真实副本(replica)的距离被强迫扩大到比正常情况大(重叠较小)时可能发生的相变。
在工作的第一部分,作者们通过解析地求解接近临界点的场中的 Sherrington-Kirkpatrick 模型,发现即使在顺磁相,强迫两个真实副本的重叠足够小会导致模型发生相变,副本之间的对称性自发破缺。更重要的是,这种相变与de Almeida-Thouless (dAT) 临界线有关。在工作的第二部分,作者们利用两个真实副本之间重叠的相变,来识别有限维自旋玻璃中场中的临界线。因为需要进行大量的有限尺寸修正,这个计算问题的困难众所周知。
作者们为无序系统引入了一种分析蒙特卡罗数据的新方法,其中两个真实副本之间的重叠被作为一个条件变量。然后这种分析被应用于 d =1 自旋玻璃模型场中顺磁相的平衡测量, 这里自旋玻璃模型具有长程相互作用,衰减得足够快,超出了平均场理论的有效范围。这项工作对场中的热力学临界温度提供了非常可靠的估计。
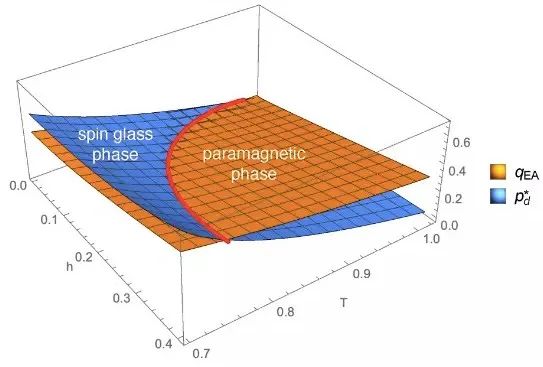
图1. 红色曲线是 dAT 临界线,分隔了顺磁相和玻璃相。在顺磁相的蓝色曲面以下,副本对称性被打破。
论文题目:Hyperscaling Violation in Ising Spin Glasses
论文地址:https://www.mdpi.com/1099-4300/21/10/978
物理系统的微观结构和宏观现象可能不尽相同,但在临界点附近,却可能表现出类似的相变行为,遵循显著的幂律关系,具有相同的临界指数。而且这些临界指数并非彼此独立,而是通过标度律(scaling rule)联系起来。如果再引入系统的空间维数,则得到超标度律(hyperscaling rule)。对于朗道相变理论,超标度关系通常并不成立,当且仅当空间维度 d=4 时,超标度关系才成立。
Edwards–Anderson 伊辛自旋玻璃(Ising Spin Glass)的淬火相互作用被明确假设为是随机的,遵循与标准伊辛模型相同的基本标度律和普适性。至于超标度关系,众所周知,在标准伊辛模型中,当维度超过上临界维数 d=4 时,超标度律坍塌 ;M. Schwartz 在1991年指出,超标度也可以在具有淬火随机相互作用的伊辛系统中被破坏,属于这类系统的随机场伊辛模型已经被深入研究。本文主要研究伊辛自旋玻璃中超标度违反的证据。
文章给出了3、4、5、7维情况下,将归一化 Binder 累积量与约化关联长度联系起来的数值伊辛自旋玻璃数据。在3、4维以及超过上临界维数时,超标度明显被违反。研究得到了各种模型中违反超标度指数数值的估计。
(Four) Dual Plaquette 3D Ising Models
https://www.mdpi.com/1099-4300/22/6/633
三维元格(Plaquette)伊辛模型的一个特征是其平面子系统的对称性。已证明该模型的量子版本通过对偶性与 X-Cube 模型相关联,X-Cube 模型是快速发展的分形子(fracton)领域的一个范例。三维元格伊辛模型与 X-Cube 模型之间的关系,类似于二维量子横向自旋伊辛模型与 Toric 编码之间的关系。计算二维伊辛模型的全局对称性并考虑高温相的规范不变区产生了 Toric 编码,而计算三维量子横向自旋元格伊辛模型的子系统对称性则产生了 X-Cube 模型。
在对偶化 X-cube 模型无分形子部分的语境下,一个利用三种自旋的非标准对偶形式的三维元格伊辛模型最近引发讨论。本文研究了这种非标准对偶哈密顿量的经典自旋版本,并讨论了它与更为熟悉的类 Ashkin-Teller 对偶及其相关对偶公式的关系,以及更远的包括边和顶点自旋与非伊辛自旋的对偶形式的关系。
图2. 在三维元格伊辛模型的一个立方体的一个面上,翻转自旋并不会改变能量。图中第一个立方体是反铁磁态,所有自旋为+;其他三个立方体的阴影面的角上的自旋为−,其他自旋为+。所有四种自旋构型有相同能量。
Exact Recovery of Stochastic Block Model by Ising Model
https://www.mdpi.com/1099-4300/23/1/65
在网络分析中,社团检测(community detection)是指推断图中连接更密集的顶点集合。社团检测已被应用于许多领域,包括推荐系统、分布式计算中的任务分配、基因表达等。随机块模型(Stochastic Block Model)是社团检测问题中最常用的统计模型之一。
随机块模型是随机图的生成模型,它倾向于生成包含社团的图,常作为恢复图数据中社团结构的基准。恢复社团的任务分为精确恢复(exact recovery)与部分恢复(partial recovery),前者要求算法估计的社团与随机块模型的社团结构完全相同,后者要求算法尽可能减小错误分类的节点比例。通常会分析当图的规模趋于无穷大时,检测误差的渐近特性。
本文研究定义在随机块模型上的伊辛模型的相变特性。在伊辛模型(节点状态的概率分布)的基础上,文章提出了一种随机估计方法来实现随机块模型的精确恢复。随机算法可以转化为一个优化问题,其中包括最大似然和最大模块化的特殊情况。此外,本文给出了随机块模型参数的无偏收敛估计,该估计可以在恒定时间内计算。最后,利用 metropolis 采样实现了随机估计,并通过实验验证了相变现象。
Kinetic Models of Discrete Opinion Dynamics on Directed Barabási–Albert Networks
https://www.mdpi.com/1099-4300/21/10/942
复杂网络广泛应用于自然中的网络和人的网络,除此之外,复杂网络上的自旋系统也可用于研究相变特征,以及临界行为对应的普适性类。在有向 Barabási-Albert(BA)网络中,已经证明最近邻自旋 1/2 伊辛模型没有相变,但非平衡多数投票模型(majority-vote model)表现出有序-无序动态相变。2012年,Biswas、Chatterjee、Sen 引入了连续(或离散)意见动力学模型,BCS 模型可以具有正的或负的相互作用,连续 BCS 模型的数值模拟表明存在普遍的连续相变。
本文利用 Monte Carlo 模拟方法,研究了有向 BA 网络上的离散意见动力学模型,即 BCS 模型的离散版本,发现该体系存在连续相变。研究得到了这些有向网络的几个连通度值的噪声参数临界值。此外还计算了序参数的临界指数之比与关联长度的感应强度。作者们注意到,临界指数之比随着网络连通性的变化而变化,这些有向 BA 网络上的动力学模型和多数投票模型属于同一普适性类。
Universality and Exact Finite-Size Corrections for Spanning Trees on Cobweb and Fan Networks
https://www.mdpi.com/1099-4300/21/9/895
普适性的概念是临界现象理论的基石。对于大多数系统,特别是在热力学极限下,普适性都得到了很好的理解。然而,在有限系统的修正项中,边界特征是明显的。对有限尺寸标度和标度修正的理论研究,包括外推有限或部分有限系统,以确定它们对应的无限系统的临界和非临界性质。
有限尺寸系统带来了挑战。即使在低维,边和角对自由能和响应函数的贡献的普适性也很少被研究和理解。特别是有一个问题,属于同一普适性类、但具有非常不同角几何的系统,在标度修正中如何保持普适性。
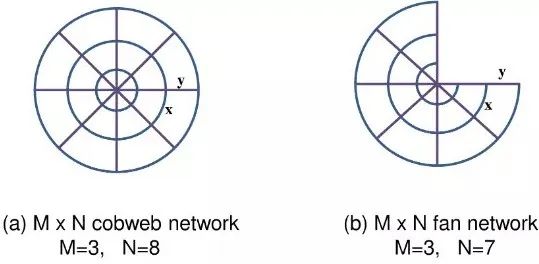
二维几何提供了最简单的例子,可以构造有角和没有角的图形。为了研究角的存在和不存在如何体现普适性,本文分析了两种不同的有限系统,即蛛网(cobweb)和扇形网络(fan network)上的生成树(Spanning Tree)生成函数。生成树是一个连通图的子图,表示将结构中每个节点链接起来的最有效方式。有限尺寸的蛛网没有角,而扇形网络有四个角。因为期待了解它们的普适特性,这些构型的角自由能激发了人们极大的兴趣。
2002年,Ivashkevich、Izmailian、Hu 开发了一种方法,可以为各种基本函数,比如配分函数及其导数,提供精确的有限尺寸修正。该方法被应用于多种统计物理模型中,如伊辛模型、二聚体模型和高斯模型,结果表明,每个模型的配分函数都可以写成具有扭曲边界条件(twisted boundary condition)的一般配分函数。
这项研究使用 Ivashkevich-Izmailian-Hu 方法,将不同网络的生成函数统一为具有扭曲边界条件的单个配分函数。这种统一方法表明,扇形网络四个角的自由能相互抵消,贡献之和为零,因此与没有角的蛛网网络的贡献一致。因此,它也符合共形理论(其中心电荷为 c=−2)和有限尺寸标度预测。
该研究验证了 Ivashkevich-Izmailian-Hu 算法的稳健性。其广泛的有用性体现在可以应用到迄今为止尚未解决的问题——即生成函数对数的精确渐近展开,以及扇形和蛛网几何的共形配分函数。作者们还研究了带状几何(strip geometry),再次证实了共形场论的预测。因此,普适性难题的解决证明了算法的强大,并开辟了未来的新应用。
图3. (a) M=3, N=8 的 M×N 蛛网网络。(b) M=3, N=7 的 M×N 扇形网络。
跨尺度、跨层次的涌现是复杂系统研究的关键问题,生命起源和意识起源这两座仰之弥高的大山是其代表。而因果涌现理论、机器学习重整化技术、自指动力学等近年来新兴的理论与工具,有望破解复杂系统的涌现规律。同时,新兴的因果表示学习、量子因果等领域也将为因果涌现研究注入新鲜血液。
集智俱乐部特别组织「因果涌现」系列读书会,深入研读相关文献,激发科研灵感。目前已经进行了两季,聚集了500+成员,积累了大量论文解读资料。欢迎感兴趣的朋友报名,加入因果涌现社区,并解锁对应录播权限。
读书会详情与报名方式请参考:
因果涌现读书会启动:连接因果、涌现与自指——跨尺度动力学与因果规律的探索
因果、涌现与机器学习:因果涌现读书会第二季启动