本文简要介绍了幂律函数 (power laws) 和关联函数 (correlation functions) 是如何度量临界性 (criticality) 的及它们之间的关系。通过比较降雨、大脑和森林火灾模型的现象学 (phenomenology),我们讨论了临界状态附近自组织的相关特征。得到结论:系统(自)组织到一个具有广义相关性和近似幂律的区间,是上述三种系统可能共有的演化特征。
关键词:自组织临界,混沌边缘,幂律,关联函数,长程相关
Henrik Jeldtoft Jensen | 作者
朱欣怡 | 译者
刘培源 | 作者
邓一雪 | 编辑
论文标题:
What is critical about criticality: in praise of the correlation function
https://iopscience.iop.org/article/10.1088/2632-072X/ac24f2
研究人员对临界点及其附近状态的研究兴趣从20世纪研究物理学中的二阶相变开始,在重整化群论 (renormalisation group theory) 中达到顶峰[1]。20世纪80年代“混沌边缘”[2]和“自组织临界性”(SOC)[3]等概念在不同的领域中被创造,动力系统理论和高维非平衡统计力学的方法受到超敏感临界状态的特殊性质的启发,并被寄予希望能找到一种机制解释这种似乎无处不在的非凡现象。
虽然混沌边缘和临界性有时以一种有点松散的描述方式同义使用[4,5],但这两个概念都有精确的数学定义,并且只有当系统的控制参数被调整到一定值时才发生。
如果李亚普诺夫输出为正,那么动力系统就是混沌的。[6]。即使只涉及一些参数(通常表示为自由度)也可能发生混沌行为。如果可以通过迭代映射来表示时间演化,例如具有非重叠世代的物种(例如一年生昆虫)的种群大小,则即使对于一维自由度xn也可能出现混沌现象。最著名的可能是由下述方程给出的logistic映射[7]
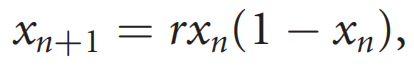 (1)
当参数r大于r∞≈3.57时,上述系统出现混沌现象。
相比之下,严格来讲,平衡统计力学的临界状态只能发生在无限多自由度的极限中。临界状态的标志是长程相关[1]。Ising 模型是支持临界状态的原型系统。基础的模型由自旋变量Si±1,i=1, 2,…,N组成,i 标记线性扩张 L 的 d 维超立方体上的位置,因此N=Ld。方差系数:
(1)
当参数r大于r∞≈3.57时,上述系统出现混沌现象。
相比之下,严格来讲,平衡统计力学的临界状态只能发生在无限多自由度的极限中。临界状态的标志是长程相关[1]。Ising 模型是支持临界状态的原型系统。基础的模型由自旋变量Si±1,i=1, 2,…,N组成,i 标记线性扩张 L 的 d 维超立方体上的位置,因此N=Ld。方差系数:
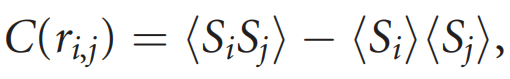 (2)。
其中rij是位置 i 和位置 j 之间的距离,用来衡量不同位置之间的相互依赖性。C(rij)在统计学中表示方差,但在统计力学文献中,它总是作为关联函数出现。我们将坚持这一传统。相关性C与相互依赖性r=rij的依赖关系能用如下数学形式表示:
(2)。
其中rij是位置 i 和位置 j 之间的距离,用来衡量不同位置之间的相互依赖性。C(rij)在统计学中表示方差,但在统计力学文献中,它总是作为关联函数出现。我们将坚持这一传统。相关性C与相互依赖性r=rij的依赖关系能用如下数学形式表示:
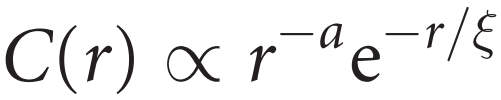 (3)
(3)
这里ξ被称为关联长度,在非临界状态长度尺度有限。调整温度T到临界温度Tc可以达到临界状态。当T接近Tc时,关联长度ξ趋于无穷大。ξ(T)→∞。
T≠Tc时,距离r小于ξ,如r<<ξ时,关联函数将代数衰减,呈幂律分布C(r)~r-a。距离r大于ξ,如r>>ξ时,关联函数指数衰减,C(r)~e-r/ξ。
只有在临界状态T=Tc时,无论距离r有多大,相关性都将按照幂律C(r)∝r-a缓慢衰减,而且由于ξ →∞,故不存在单一的特征尺度区分空间和时间。我们说这个状态就具有尺度不变性,是因为不考虑放大因子时,它在所有的空间和时间尺度上的表现都一致。因此,空间结构应为分形结构。概率分布,比如那些描述对外部扰动的响应,应遵循幂律分布。
自组织临界性[3,8,9]给出:许多不平衡的系统,在动力的缓慢驱动下,会自组织到刚刚描述的临界状态。原始论文[3]的基本原理是,由于临界状态是标度不变的,因此可以通过研究自组织系统发生能量耗散爆发(传统上称为雪崩)的概率分布来研究临界性,雪崩是逐渐增加应力的结果。如果这样的分布服从幂律分布,我们就能研究临界状态,尽管不能直接检验方程(2)中的关联函数代数上依赖分离。这是一个明智的研究起点,但它并不总是正确。
事件大小的分布服从幂律分布,即使各个弛豫事件发生雪崩完全独立。典型的例子有不相关分支过程和独立随机游走。
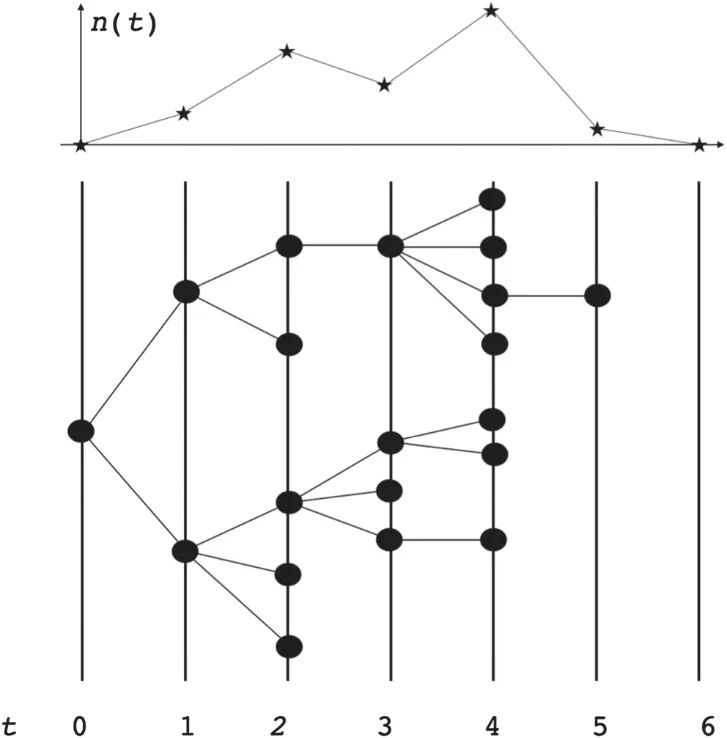
简单回顾一下,不相关分支过程由可以产生子代的“节点”组成。把每个节点看作一个神经元,它的子代就是从第一个节点接收电信号的节点。图1显示了该过程。每个节点产生k个具有相同独立概率pk的后代,k = 1,2,……。生成树的大小S,即根节点产生的节点总数,遵循以下形式的分布[10]:
 (4)
(4)
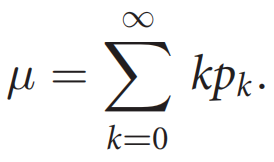 (5)
当分支比μ等于1时,该过程为临界过程。因为当μ接近1时,尺度S0按照S0~(1-μ)-2发散。参见等式(4),这意味着临界分支过程发生雪崩的概率分布由3/2指数的幂律描述。
一个分支过程的实现。每个节点以相同的独立概率pk产生k个后代(k = 0,1,2,…)。时间以世代t为单位计算,树的演化或雪崩由n(t)表示,n(t)是第t代的节点数(见上图)。雪崩的持续时间T是从第t = 0代到n(t)>0的最后一代,如图中T= 6。
雪崩的持续时间由总代数T(直到没有根节点的新后代产生为止)给出,参见图1。当分支比达到临界值μ = 1时,持续时间的分布也变成幂律,P(T)~T-2。
为什么不相关事件能产生无标度幂律分布。因为根初始化后,代际t中节点数的变量n(t)是相关的。尽管各节点产生后代独立,但第t+ 1代的节点数显然与上一代的节点数n(t)相关。如果在第t代中有许多节点,即n(t)较大,则与n(t)较小的情况相比,第t + 1代中的节点数也更可能较大。但这种相关性并不是很深刻。
随机游走信号f(t)的情况类似。如果f(t+1)= f(t)+Δt,其中Δt是相同分布里取得的独立随机数,则f(t+1)-f(t)的变化是独立的随机数,但信号f(t)仍然具有幂律特征。例如,考虑第一次返回乘以T的分布。第一次返回时间是f(t+T)之前的时间T,假定第一次返回值f(t)的时间为t。这种分布遵循幂律T-3/2。
在概括了不相关的随机过程可以产生雪崩的幂律分布之后,更重要的问题是刚刚的讨论与大脑是否表现出临界行为有多大的相关性,更具体地说,自组织临界性与大脑动力学有多相关性?以及如何相关?我们先回顾一下,已有研究发现:在不同尺度上观察到的大脑神经元活动雪崩呈指数为3/2和2的幂律分布。众所周知,在数百个神经元集体放电产生的局部场电位上,Beggs和Plenz [11]用功能性磁共振成像(fMRI)检测的雪崩分布呈指数为3/2和2的幂律分布,Chialvo及其合作者也观察到了雪崩幂律分布的3/2指数。
然而,我们应该记住,精确确定指数很困难,现在有研究员[13]已经提出了研究幂律分布行为的替代方案。不过我们在这里的重点略有不同,我们要研究:换言之,在长程相关性方面,即便是仅仅是近似幂律的行为也仍然有趣。
即使在自组织临界性的框架内,这些指数的准确值以及它们如何依赖于大脑活动的细节也一直是详细讨论的焦点,参见[14]及其参考文献。这里我们只想强调,虽然单个神经元雪崩可能表现出分支比等于1的不相关分支过程的指数特征,但雪崩之间的等待时间分布表明每个雪崩的开始是相关的。众所周知,如果神经元在每个时间单位内以恒定的概率发生雪崩,即为泊松过程,那么雪崩之间的时间将成指数分布。对比分析表明,等待时间服从幂律分布[14,15]。[16]从功能性磁共振成像中提取的空间和时间相关性补充了相关脑活动的指标,并观察到空间分离函数的幂律衰减以及1/f时间功率谱,表明时间相关性为对数衰减。因此,通过相关临界状态之间的自组织过程,更好地理解系统的各个方面,确实仍具价值。
在下一节开始讨论之前,我们还要说明另一个关于自组织临界性雪崩动力学相关性的迹象。De Arcangelis及其合作者在一系列工作中发展了受自组织临界性启发的模型[17],开发这些模型是为了分析抑制[14、15]、模块化结构[18]、突触可塑性的理论[19]的重要性,甚至解决了雪崩动力学如何能够支持神经网络中的模式识别[20]。大量工作表明,自组织临界性启发的建模和分析方法在讨论非临界性问题时也很有意义。
(5)
当分支比μ等于1时,该过程为临界过程。因为当μ接近1时,尺度S0按照S0~(1-μ)-2发散。参见等式(4),这意味着临界分支过程发生雪崩的概率分布由3/2指数的幂律描述。
一个分支过程的实现。每个节点以相同的独立概率pk产生k个后代(k = 0,1,2,…)。时间以世代t为单位计算,树的演化或雪崩由n(t)表示,n(t)是第t代的节点数(见上图)。雪崩的持续时间T是从第t = 0代到n(t)>0的最后一代,如图中T= 6。
雪崩的持续时间由总代数T(直到没有根节点的新后代产生为止)给出,参见图1。当分支比达到临界值μ = 1时,持续时间的分布也变成幂律,P(T)~T-2。
为什么不相关事件能产生无标度幂律分布。因为根初始化后,代际t中节点数的变量n(t)是相关的。尽管各节点产生后代独立,但第t+ 1代的节点数显然与上一代的节点数n(t)相关。如果在第t代中有许多节点,即n(t)较大,则与n(t)较小的情况相比,第t + 1代中的节点数也更可能较大。但这种相关性并不是很深刻。
随机游走信号f(t)的情况类似。如果f(t+1)= f(t)+Δt,其中Δt是相同分布里取得的独立随机数,则f(t+1)-f(t)的变化是独立的随机数,但信号f(t)仍然具有幂律特征。例如,考虑第一次返回乘以T的分布。第一次返回时间是f(t+T)之前的时间T,假定第一次返回值f(t)的时间为t。这种分布遵循幂律T-3/2。
在概括了不相关的随机过程可以产生雪崩的幂律分布之后,更重要的问题是刚刚的讨论与大脑是否表现出临界行为有多大的相关性,更具体地说,自组织临界性与大脑动力学有多相关性?以及如何相关?我们先回顾一下,已有研究发现:在不同尺度上观察到的大脑神经元活动雪崩呈指数为3/2和2的幂律分布。众所周知,在数百个神经元集体放电产生的局部场电位上,Beggs和Plenz [11]用功能性磁共振成像(fMRI)检测的雪崩分布呈指数为3/2和2的幂律分布,Chialvo及其合作者也观察到了雪崩幂律分布的3/2指数。
然而,我们应该记住,精确确定指数很困难,现在有研究员[13]已经提出了研究幂律分布行为的替代方案。不过我们在这里的重点略有不同,我们要研究:换言之,在长程相关性方面,即便是仅仅是近似幂律的行为也仍然有趣。
即使在自组织临界性的框架内,这些指数的准确值以及它们如何依赖于大脑活动的细节也一直是详细讨论的焦点,参见[14]及其参考文献。这里我们只想强调,虽然单个神经元雪崩可能表现出分支比等于1的不相关分支过程的指数特征,但雪崩之间的等待时间分布表明每个雪崩的开始是相关的。众所周知,如果神经元在每个时间单位内以恒定的概率发生雪崩,即为泊松过程,那么雪崩之间的时间将成指数分布。对比分析表明,等待时间服从幂律分布[14,15]。[16]从功能性磁共振成像中提取的空间和时间相关性补充了相关脑活动的指标,并观察到空间分离函数的幂律衰减以及1/f时间功率谱,表明时间相关性为对数衰减。因此,通过相关临界状态之间的自组织过程,更好地理解系统的各个方面,确实仍具价值。
在下一节开始讨论之前,我们还要说明另一个关于自组织临界性雪崩动力学相关性的迹象。De Arcangelis及其合作者在一系列工作中发展了受自组织临界性启发的模型[17],开发这些模型是为了分析抑制[14、15]、模块化结构[18]、突触可塑性的理论[19]的重要性,甚至解决了雪崩动力学如何能够支持神经网络中的模式识别[20]。大量工作表明,自组织临界性启发的建模和分析方法在讨论非临界性问题时也很有意义。
现在我们转而讨论新问题:临界态的自组织是怎样发生的,以及不同系统和模型上的临界态自组织有何相同点。理解上述问题,会让我们发现,即使没有完美调整到平衡的临界状态,但从事件分布的尺度来判断,统计力学仍然有效,有趣的长程相关性仍然重要、并且在操作上是可得的。
我们将详细介绍Chialvo及其合作者的观察结果:通过功能磁共振成像[12,21]监测的大脑活动爆发的时空统计与大气降水活动[22]具有显著的共同性。而且,大脑活动和降水量的统计数据与森林火灾模型(FFM)[24]的自组织临界性非常相似[23]。
简单介绍一下森林火灾模型。模型的动力学可以形象地表示为某种活动在人群中的传播。该模型考虑了d维的超立方晶格,这里我们只讨论d = 2的结果,并且使用含有N=L2个格点的尺寸为L的正方体晶格。每个位置可以有三种状态:没有树E、包含树T或包含着火的树F。基本的演化过程为:
1.选择一块空地;
2.以p的概率种一棵树:E→T;
3.随机选择一棵树并点燃它,比如以f的概率:T→F;
4.下一时刻,正在燃烧的树的邻树也烧起来:T→F;
该模型已被广泛研究,近期的模拟研究可以参见[25]及其参考文献。
当f取极限f<<p时,即外部点火非常罕见时。在这个极限中,动力学的显著特征在于形成连接簇。由于几乎没有外界点火,那么我们可以认为,在外部点火所代表的外部能量输入的时间尺度上,连接簇是被瞬间烧毁的。模拟结果表明,被烧毁的团簇的尺寸分布近似服从幂律分布。但是,模型中的临界性和规模不变性也并不寻常[26,27]。例如,Grassberger [26]提出,比值θ = p/f足够大时,只要系统大小足够大,大到可以容纳生成的巨大树簇,就可能会表现出渗流中的缩放。这可能是真的,但[28]的分析表明,只有当θ>1040时才能观察到这种缩放,而且为了避免模拟受到系统大小的影响,还需要达到难以达到的系统大小,即线性大小为L~1040 [25]。
我们由此得出结论,虽然真正的渐近(系统规模趋于无穷大)行为目前还无法实现,但必须指出,通过仿真研究系统规模的模型表现确实有效,可以深入了解自组织临界性与真实的系统的相关性。
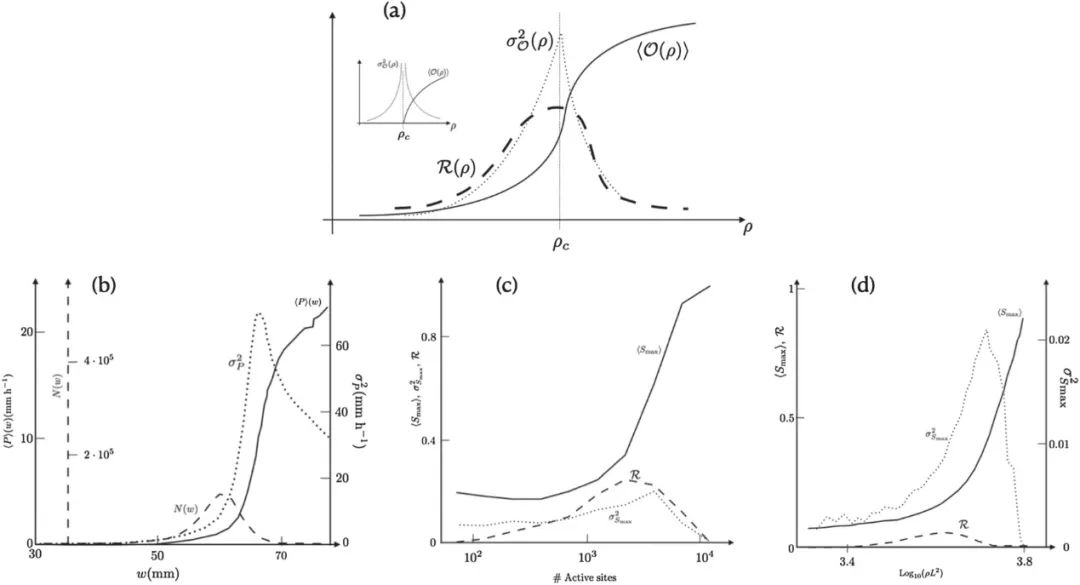
Peters和Neelin [22]曾观察到,当绘制降水量与大气湿度图时,在狭窄的湿度范围内可以看到一个急剧的开始。图2显示了降雨、大脑活动和森林火灾模型的表现。
(a) 一般性草图,类似于平衡相变的临界状态。这三条曲线:实线表示序参量,长虚线表示驻留时间,虚线表示方差(在平衡系统中相当于磁化率)。在一个临界平衡相变(如插图所示)中,如伊辛模型和磁性系统,序参数在相变的一侧严格为零,然后在一个尖锐的值处变为非零,临界值为pc,磁化率在pc处发散。因为控制参数ρ是外生的,所以无需考虑平衡系统中的驻留时间。
(b)降水量,参考[22]中图1和图3绘制。x轴表示大气中的蒸汽含量。实线表示序参量,如降水量。虚线是方差,长虚线是观察到特定值w的次数,即驻留时间。
(c)大脑活动,参考[12]中图3(E)绘制。x轴表示活跃体素的数量。实线表示序参量,即归一化为活跃体素数量的最大聚类的平均值。虚线表示方差,长虚线表示归一化的驻留时间。
(d)森林火灾模型,参考[23]中的图1绘制。x轴表示树所占据的位置数。实线表示有序参数,即归一化为树位点的数目的最大簇的平均值。虚线表示方差,长虚线表示归一化的驻留时间。
该图综合了文献中的四幅图。首先,参考文献[22]中的图1,该图绘制了降水量及其方差与大气中蒸汽量的函数关系。大气在某一蒸汽水平上所花费的时间如[22]中的图3所示,这个时间称为驻留时间。其次,[12]中的图3(E)显示了活性功能性磁共振成像体素簇的最大尺寸(高于特定阈值)的归一化大小,与活性体素总数、及其方差和驻留时间的函数。最后,[23]的图1中给出了类似的分析,包含最大树簇、其方差和驻留时间与树的数量(被认为是能够产生活性的场地)的函数关系。
在这三种情况下,我们都观察到所谓的序参量,即区别系统相对于临界状态的参量,在控制参量的一个相对狭窄的取值范围内,从很低的值开始上升。上述三种情况的序参数分别为:降水量、活性体素连通簇的大小和烧毁簇的大小。三种情况的控制参数分别为:大气中的蒸汽量、活性体素的数量和树木的数量。在这三种情况下,当控制参数在序参量出现和方差达峰的区域的中部附近取某个值时,观察到事件分布(分别为降水事件的数目、最大活跃体素簇的大小、最大烧毁树簇的大小)近似幂律分布。这意味着,在这三种情况下,我们都观察到了临界平衡相变中的一个急剧转变的扩展版本,参见图2中的插图。
我们要强调两点。第一,这三个完全不同的系统在如何自组织的方面惊人的相似,它们是如何组织自己的,所以它们频繁出现在表现出潜在的近临界转变的区域中。第二,尽管大脑和大气都是非常大的系统,但它们都具有森林火灾模型的有限大小属性。这表明,与平衡临界现象相反,我们知道在发散系统尺寸的限制下理解渐近行为至关重要,结合自组织临界性的雪崩动力学考虑,有限系统的尺度表现特别有趣。另一方面,这意味着,应用自组织并不是自组织到一个明确定义的临界点,而由动力学将自身带到某个接近临界行为的区域的趋势组成。
那么问题仍然是什么使这个区域趋近某种临界状态。因此,我们回到关联并回想起平衡临界态的幂律和发散灵敏度(磁化率)都是长程代数关联的结果。是否有证据表明,这三个系统驻留时间的峰值出现的区域与方程(3)所描述的相关性有关?关联长度ξ足够大使得缓慢的幂律衰减r-a能够基本上决定系统行为。
大气系统的结论还未可知。[16]中用功能磁共振成像研究血氧信号相关性表明,大脑就是这种情况。最近的森林火灾模型研究证实,尽管事件分布的标度令人困惑,但空间相关性总是长程的[28]。在这种方法中,可以认为关联长度是一个随机变量。对于上述系统的每个瞬时构型,将方程(2)中的关联函数拟合为方程(3)中的函数形式,以确定描述该特定构型的关联长度ξ。这一方法不同于平衡系统研究中确定关联长度的常见方法。仿真法通常首先在所有生成的构型上对方程(2)中的关联函数求平均,然后从对该平均函数的拟合中提取关联长度。[28]中发展了新方法,该方法将关联长度作为每个单独构型的特征,以重现两个原型模型的已知平衡行为,如伊辛模型和二维XY模型。更有趣的是,该方法为森林火灾模型中的相关性提供了新的理解。
对于森林火灾模型,当变量Si=1时表示有树,Si=0时表示该位置为空。忽略火灾燃烧点,因为火灾在单个时间步长以p为生长概率移除连接簇。当模拟树生长和火灾动力学时,对瞬时构型的关联长度的分布P(ξ)进行采样。模拟发现,对于L = 3000的系统,分布P(ξ)用有限系统的尺度可以很好地描述,这意味着当L变化时,当θ/L2给出的每个位点的活性保持不变时,不同L值的P(ξ)可以坍缩为一个“通用”函数。对系统大小的依赖性表明:从分布P(ξ)提取的平均关联长度依赖于系统大小,如<ξ>∝L1.1。这表明,随着L的增加,当由火灾概率f给出的动力与生长概率p趋于无关时,比如当外生动力很慢时,系统的相关性会趋于长程。
我们注意到,首次用自组织临界性精确调整到预期临界点似乎没有在降雨、大脑和森林火灾模型中发生。这并没有让自组织临界性框架变得无关紧要。相反,自组织现象确实发生在序参量上升的区域附近。此外,对森林火灾模型的研究表明:虽然事件分布的幂律可能只是近似的,但这三个系统耗时最多的区域却与非常广大的空间相关性之间,相互关联。
不同系统的共有规律表明:由负载、传播和弛豫驱动的动力学的基本成分倾向于组织成接近某种(相关)渗流开始的构型。空间扩展结构的建立,然后通过降水,神经元放电或火灾在上述三种情况下分别突然崩溃,不断地将“超过临界”的构型转变为“低于临界”的构型。
森林火灾模型的模拟表明:对于可管理的参数状态,可优先访问构型的区域,比如驻留时间分布中峰值周围的区域,随着由负载(树木生长)和能量释放触发(外部诱导火灾)给出的两个时间尺度之间的间隔(即θ=p/f)的增加而加宽。森林火灾模型中驻留时间的峰宽近似为σ~θ0.1,见[25]。因此,将模型推向更扩展的幂律和更长的关联长度也扩大了访问临界构型和临界构型的范围。
结论是,流入-流出动力学并不能微调到临界点,但是可以微调到扩展相关性的区域。
这一点在之前就已经有人提出过,例如[13,29,30],但在这里我们要强调的是,尽管没有达到严格的临界性,但相关性足够广泛,足以使三个完全不同的系统(降水,大脑和森林火灾模型)中的流入-流出动力学具有显著的相似性。
人们常常认为,大脑在临界点或其附近工作的原因是这种状态具有超敏性(表现为磁化率的发散)。看起来很合理,但为什么大脑没有处于临界状态呢?如Lizier及其合作者[31]所说,大脑可能在临界点区域内操作更有计算优势,因为它将亚临界区域的高数据存储能力与超临界区域内更快的信息传递结合起来。所以,无法精确调整到临界状态可能也不失为一件好事。
[1] Goldenfeld N 1992 Lectures on Phase Transitions and the Renormalization Group (Boca Raton, FL: CRC Press)
[2] Packard N H 1988 Adaptation Toward the Edge of Chaos (Champaign, IL: University of Illinois) Urbana-Champaign, Center for
[3] Bak P, Tang C andWiesenfeld K 1987 Self-organized criticality: an explanation of the 1/f noise Phys. Rev. Lett. 59 381–4
[4] Barras C 2013Mind Maths; your brain teeters on the edge of chaos. NewScientist https://institutions.newscientist.com/article/
mg21729032-100-mind-maths-your-brain-teeters-on-the-edge-of-chaos/
[5] Washington University in St 2019 Brain tunes itself to criticality, maximizing information processing: criticality is a hallmark
of normally functioning neural networks in the intact brain. ScienceDaily www.sciencedaily.com/releases/2019/10/191007113314.htm
[6] Ott E 1993 Chaos in Dynamical Systems (Cambridge: Cambridge University Press)
[7] May RM 1976 Simple mathematical models with very complicated dynamics Nature 261 459
[8] Jensen H J 1998 Self-Organized Criticality: Emergent Complex Behaviour in Physical and Biological Systems (Cambridge: Cambridge University Press)
[9] Pruessner G 2012 Self-Organized Criticality: Theory, Models and Charaterisation (Cambridge: Cambridge University Press)
[10] Harris T E 1963 The Theory of Branching Processes (Berlin: Springer)
[11] Beggs J M and Plenz D 2003 Neuronal avalanches in neocortical circuits J. Neurosci. 23 11167–77
[12] Tagliazucchi E, Balenzuela P, Fraiman D and Chialvo D R 2012 Criticality in large-scale brain fMRI dynamics unveiled by a novel
point process analysis Front. Physiol. 3 1–12
[13] Wilting J and Priesemann V 2019 25 years of criticality in neuroscience—established results, open controversies, novel concepts Curr. Opin. Neurobiol. 58 105–11
[14] Lombardi F, Herrmann H J and De Arcangelis L 2017 Balance of excitation and inhibition determines 1/f power spectrum in neuronal networks Chaos 27 047402
[15] Lombardi F, Herrmann H J, Perrone-Capano C, Plenz D and De Arcangelis L 2012 Balance between excitation and inhibition controls the temporal organization of neuronal avalanches Phys. Rev. Lett. 108 228703
[16] Paul E, Lambiotte R, Chialvo D R, Christensen K, Jensen H J, Sharp D J and Turkheimer F 2011 Self-similar correlation function in brain resting-state functional magnetic resonance imaging J. R. Soc. Interface 8 472–9
[17] De Arcangelis L, Perrone-Capano C and Herrmann H J 2006 Self-organized criticalitymodel for brain plasticity Phys. Rev. Lett. 96028107
[18] Russo R, Herrmann H J and De Arcangelis L 2014 Brain modularity controls the critical behavior of spontaneous activity Sci. Rep. 4 1–5
[19] Michiels Van Kessenich L, De Arcangelis L and Herrmann H J 2016 Synaptic plasticity and neuronal refractory time cause scaling behaviour of neuronal avalanches Sci. Rep. 6 1–7
[20] Michiels Van Kessenich L, Berger D, De Arcangelis L and Herrmann H J 2019 Pattern recognition with neuronal avalanche dynamics Phys. Rev. E 99 010302
[21] Chialvo D R 2010 Emergent complex neural dynamics Nat. Phys. 6 744–50
[22] Peters O and Neelin J D 2006 Critical phenomena in atmospheric precipitation Nat. Phys. 2 393–6
[23] Palmieri L and Jensen H J 2018 The emergence of weak criticality in SOC systems Europhys. Lett. 123 20002
[24] Drossel B and Schwabl F 1992 Self-organized critical forest-fire model Phys. Rev. Lett. 69 1629–32
[25] Palmieri L and Jensen H J 2020 The forest fire model: the subtleties of criticality and scale invariance Front. Phys. 8 1–8
[26] Grassberger P 2002 Critical behaviour of the Drossel–Schwabl forest fire model New J. Phys. 4 17.1–17.15
[27] Pruessner G and Jensen H J 2002 Broken scaling in the forest-fire model Phys. Rev. E 65 056707
[28] Palmieri L and Jensen H J 2020 Investigating critical systems via the distribution of correlation lengths Phys. Rev. Res. 2 013199
[29] Bonachela J A and Muñoz M A 2009 Self-organization without conservation: true or just apparent scale-invariance? J. Stat. Mech. P09009
[30] Bonachela J A, De Franciscis S, Torres J and Muñoz M A 2010 Self-organization without conservation: are neuronal avalanches generically critical? J. Stat. Mech. P02015
[31] Li M, Han Y, Aburn M J, BreakspearM, Poldrack R A, Shine J M and Lizier J T 2019 Transitions in information processing dynamics at the whole-brain network level are driven by alterations in neural gain PLoS Comput. Biol. 15 e1006957
集智斑图顶刊论文速递栏目上线以来,持续收录来自Nature、Science等顶刊的最新论文,追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能,每周通过微信服务号「我的集智」推送论文信息。扫描下方二维码即可一键订阅:

本篇文章来源于微信公众号: 集智俱乐部



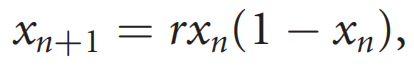 (1)
(1)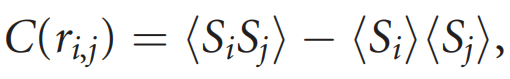 (2)。
(2)。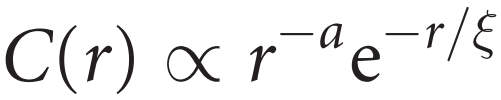 (3)
(3) (4)
(4)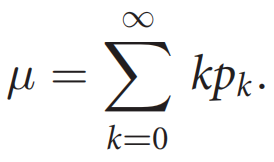 (5)
(5)