关键词：Kadanoff 超节点，异构网络，网络嵌入，重整化群，对称性

论文题目：Laplacian renormalization group for heterogeneous networks

论文来源：Nature Physics

论文地址：https://www.nature.com/articles/s41567-022-01866-8

重整化群（Renormalization group）是现代普适性（universality）原理和相变理论的基石，是检验动力系统对称性和组织尺度一致性的有力工具。然而，由于不同尺度之间的相关性相互交织，使得重整化群难以用于复杂网络。迄今为止，已有的方法都是基于隐含的几何假设，这种假设依赖于将复杂网络嵌入到底层的隐度量空间中。

近日发表于 Nature Physics 的这篇文章提出了一个基于拉普拉斯重整化群扩散的复杂网络方法，它能够在异质网络中识别合适的时空尺度，与实空间重整化群方法类似。

作者首先介绍了 Kadanoff 超节点作为多尺度块节点的概念，这有助于克服小世界效应（这是跨尺度相关性的原因）；然后严格定义动量空间过程，逐步积分得出快扩散模式并生成粗粒度图。该方法被应用于多个实际网络，验证了其有效性，证明可以在保持系统关键特性不变的情况下，对网络进行约简。基于网络的拉普拉斯性质，文章还证明了：即使可以定义出可以被重整化的无标度结构，但只有真正的标度不变网络才会在所有标度下表现出恒定的比热容，表现出某种平移不变性。

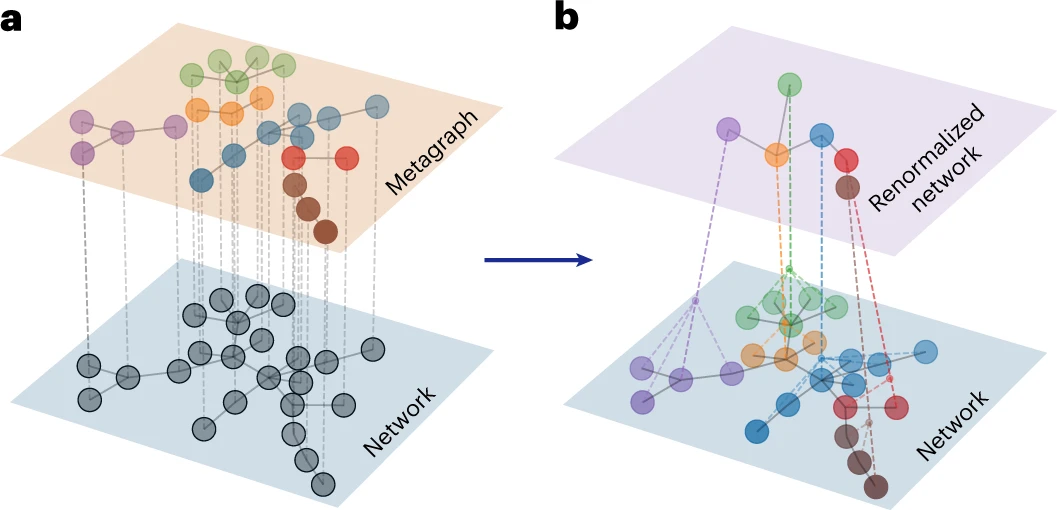
图2. kadanoff 方法的示意图

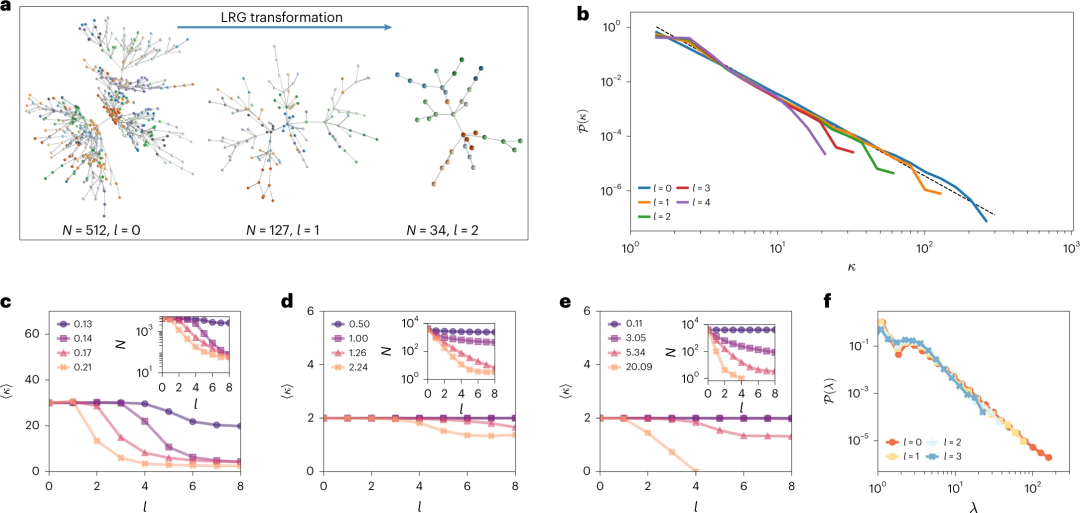
图4. 实际网络的拉普拉斯重整化变换。

网络科学集智课堂第三期：

从数学建模到多学科应用

​