摘要

社会和健康科学中使用的机器学习（Machine Learning, ML）方法需满足描述、预测、因果推断等预期研究目的。本文通过将统计分析引入这些学科，对社会和健康科学中的研究问题与ML方法进行了全面、系统的总结。我们将其分类为描述、预测、反事实预测和因果结构学习，例如，估算不良社会或健康结果的发生率、预测事件的风险、识别风险因素或不良结果的原因、解释常见的ML性能指标等。这一归纳有助于在考虑与社会和健康科学相关领域问题时，充分利用ML的优势并加快ML应用的普及，以推进基础和应用的社会和健康科学研究。

关键词：机器学习

Anja K. Leist, et al. | 作者

赵雨睿 | 译者

郭瑞东 | 审校

邓一雪 | 编辑

论文题目：Mapping of machine learning approaches for description, prediction, and causal inference in the social and health sciences

论文链接：https://www.science.org/doi/10.1126/sciadv.abk1942

目录

1. 引言

2. 将社会和健康科学问题转化为机器学习服务

3. 机器学习的基础

4. 描述中的机器学习

5. 预测中的机器学习

6. 因果推断中的机器学习

7. 机器学习表现性能评估

8. 未来展望

1. 引言

不同于诸多传统的统计方法，随着社会和健康科学领域中大型数据集的可用性增加，机器学习（Machine Learning, ML）方法有潜力改善经验分析的各个方面。这包括了预测领域中大量数据的快速处理、因果间的非线性和高阶关系以及预测准确性的提高。但是，从社会学、心理学、经济学到社会、临床流行病学和公共卫生学，机器学习方法在社会和健康领域中应用的进展相当缓慢，至今仍然是不完善的。这在一定程度上可归纳为三点，即缺乏学科之间沟通、难以将领域知识纳入社会和健康科学领域中的分析方法以及缺乏适合社会和健康科学领域的机器学习方法概述。

本文旨在将社会和健康科学的研究目标系统地映射到适当的机器学习方法，进而提供一个高水平的、非技术性的机器学习方法工具箱、解释机器学习中的常见度量标准并指导研究人员解决机器学习建模中的常见问题。本文侧重于研究问题，涉及了以人类为研究单位的数据集以及临床评估或自我报告。针对大多数使用机器学习的社会和健康科学的研究中，本文采用在静态数据集上训练的模型，即模型不是连续处理新的数据，而是依赖于队列研究或数据收集和清理结束后的调查的有限数据集。

本文综述应该被看作是对流行病学和健康研究(1) ，心理学(2)和经济学(3)等领域的机器学习导论的补充。对于一般的统计学习介绍，感兴趣的读者可以参考关于这些方法的优秀教科书(4,5)。

本文的其余内容组织如下：第二节部分概述了将社会和健康科学的研究目的映射到适当的机器学习方法的任务。第三节涵盖了部分机器学习的基础知识，特别是传统的机器学习分类、数据准备、模型建立以及机器学习的“现实世界”应用。第四节到第六节描述了机器学习方法对描述、预测和因果推理研究目的的映射，并给出了经验实例。第七节给出了机器学习性能指标的概述。第八节以展望结束全文。

2. 将社会和健康科学问题

转化为机器学习任务

简而言之，社会和健康科学中的常见研究目的可以根据研究人员的意图归类为: (i)描述现象，(ii)预测社会或健康结果，以及(iii)找到原因以及可能干预结果的原因。虽然不是所有的研究问题都可以按照这一归纳进行严格的区分，本文仍详细地介绍与描述、预测和因果推理相关的具体研究问题(6)。本文将这些研究问题映射到适当的机器学习方法中，并在可能的情况下使用实证研究作为例证。

本文所总结的ML 方法不同于数据分析中的传统方法，例如，推断统计学、统计学习以及计算科学。它们的共同点是具备处理大量数据的能力，并且建模和模型选择更多地依赖数据结构（数据驱动），而不是传统的推断统计。

当机器学习应用于社会和健康科学所研究的问题时，统计学知识和领域知识都是相关的。探索性数据分析(7)被用于总结和可视化数据主要特征，是数据分析和机器学习流程中重要的第一步。然而，不可知数据探索，即不考虑领域知识的数据分析，在大多数情况下只能提供较少的见解。社会和健康科学领域知识重要性的一些例子如下:

(1)决策树和其他机器学习算法中连续变量的偏好可能导致高估年龄作为预测因子，然而实际上，年龄与社会或健康现象的联系要少得多（例如，整个生命过程中在认知表现上的强烈异质性）。

(2)缺失的数据可能在数据驱动的分析中被确定为有意义的信息（通常如此）。然而，这需要将观察到的人群以及其感兴趣的结果进行背景化。

(3)在数据驱动分析中被确定为相关的类别在概念上可具有不同的意义，例如，教育相关的类别“其他”或“都不是”可能反映了异常低的教育水平或在国外获得的教育学位，但这需要具体化。

(4)具有不同社会人口学和社会经济学背景的个体在行为（以及调查参与）上的系统差异可能导致决定因素-结果关联存在偏差，这与健康的社会决定因素的研究高度相关。

我们注意到，最后一个例子往往意味着医疗保健中的不平等。少数群体的数据不平衡和结构不平衡可能导致不平等的 ML 算法，这有可能进一步加剧健康不平等(8)。虽然这里提出的一些机器学习方法，特别是用于因果推理的机器学习，比其他方法需要更多的领域知识。但我们认为，在所有社会和健康科学的研究问题中，大量的领域知识可以有意义地贡献领域，这是可解释性的先决条件(9)。虽然计算领域传统上强调预测（以及统计知识）的改进，但社会和健康科学往往优先考虑解释（以及领域知识）(2) 。本文旨在表明，推进社会和健康科学的科学知识是必要的。

有必要在社会和健康科学的研究人员和经过方法训练的研究人员之间建立一个流畅的对话，以避免“重新发明车轮”机器学习的研究人员可能缺乏领域知识，忽视了以前发现的与社会和健康科学高度相关的数据特征（例如，在整合数据集时对某些变量的重新编码过于简化）。相比之下，社会和健康科学的研究人员可能没有意识到算法背后的复杂数学和统计学以及改进机器学习方法的快速发展。总的来说，根据我们自己的经验，我们建议跨学科的合作，邀请数据科学和机器学习专家在社会和健康科学领域做研究，并希望这里提出的映射将促进不同学科的相互理解。

3. 机器学习的基础

在转向机器学习进行描述、预测和因果推断之前，我们首先简要介绍了机器学习，从(i)传统的机器学习分类(ii)数据准备(iii)模型建立以及(iv)现实世界中机器学习的可信度。

3.1 传统机器学习方法的分类

从数据科学的角度来看，大多数机器学习方法可以分为无监督式学习、有监督式学习和强化学习三个主要分支:

（1）无监督式学习是指从未标记的数据中学习模式的算法，即，从未被人类标记的变量中学习模式的算法。例如，无监督式学习将根据相似性对数据样本进行分类。

（2）有监督式学习旨在通过标记数据学习一个将输入映射到输出的函数，即为输出变量的类别分配有意义的标记或标签。在社会和健康科学中，输入被称为预测因子、自变量或暴露; 输出被称为结果或因变量。有监督式学习需要有标签的训练数据，并且可以在有标签的测试数据集中进行验证。将把神经网络（通常称为人工神经网络）作为预测算法的一个例子，把贝叶斯加性回归树（Bayesian Additive Regression Trees, BART）作为因果推理的 ML 的一个例子。惩罚回归，如最小绝对收缩和选择算子（Least Absolute Shrinkage and Selection Operator, LASSO）基于其预测能力降低了模型中变量的数量，并有助于得到既简约又表现良好的模型。

（3）强化学习是指智能体根据累积报酬的概念对环境做出决策并进行改进，即智能体会根据环境的反馈来改变和优化输入。强化学习可以应用于数据生成的情况，即在其他特征（变量）的控制下操纵治疗变量（所谓的 A/B 测试）是可能的。

作为一种学习技术，迁移学习使用多个数据源从一个数据集学习知识，并将这些知识迁移到包含不同人群的另一个数据集，甚至可能包含不同的结果(10)。因此，迁移学习将学到的特征从一种情况转移到另一种情况（一致的），从而确定各种情况下模式和行为的共同部分。因其经常与有标签数据一起使用，故被认为是监督机器学习的一种特殊方法。但迁移学习方法在其他领域也得到了一定的发展，例如，在无监督式学习、图像识别以及本文未提及的领域。本文将提出采用迁移学习减少数据不平衡的影响(11)。

3.2 数据准备

与传统的统计学不同，机器学习需要认真的数据准备。在接下来的文章将讨论与机器学习相关的几个方面: (i)数据需求、(ii)特征选择以及(iii)特征工程。三者之中，后两个是关于准备算法理解的因果变量的方式(1,12)。

3.2.1 数据需求

本文所介绍的大多数机器学习方法都需要比传统建模更大的数据集，以期在未训练数据集中表现性能优于传统建模。数据的某些方面应该具有很大的数量，如时间点、变量或个体。虽然数目具体取决于数据和机器学习方法，一般而言是有几万个数据点可用。但是，一些应用程序可以使用非常小的数据集进行探索性分析(1)。如后面所讨论的，所需要的数据点数量取决于数据维度（例如预测因子的数量）、模型复杂度、未知真实的稀疏性以及数据生成机制的复杂度(13)。因此，ML方法可应用于fat datasets（特征的数量远大于样本大小）。该数据集中潜在的信号被认为是非常稀疏的。与非机器学习的数据分析类似，认真处理数据（例如在协调过程中）并且深入理解数据来自哪里、能告诉我们什么（以及不能告诉我们什么）是至关重要的。机器学习的工作流程已经在几篇介绍性的论文中描述过，详见(1)。注意到联邦学习考虑了数据保护的法律要求，即机器学习算法的分散训练不需要跨平台交换数据。因此，联邦学习需要一个统一的数据收集和分析框架才能取得成功。

3.2.2 特征选择

特征选择通常是研究人员指导下的变量选择。这可以基于领域知识来实现，或者通过采用最小冗余最大相关性的标准或其他特征选择标准(14)来实现数据驱动。研究人员指导的特征选择可能对大型数据集有帮助，例如经济合作与发展组织（Organisation for Economic Co-operation and Development’s multicountry, OECD）的多国跨部门国际学生评估计划或者来自健康和退休家庭研究的纵向协调老龄化调查。

在选择要纳入模型的特征时，研究人员应该始终注意维数灾难。维数灾难描述了随着问题维度的增加，测试误差也会增加的趋势，除非额外的特征与响应真正相关（即不仅仅增加噪音）。更多的特征，即模型中的变量，增加了问题的维数，加剧了过拟合的风险。因此，可以收集数千甚至数百万特征的数据采集方面的进展是一把双刃剑。如果特征真正相关，样本具有代表性，那么可以提升预测效果。但如果不是，将会导致更加有偏的结果。此外，即使它们是相关的，偏差的减少可能会被增加的方差抵消(5)。稀疏恢复的 Donoho-Tanner 相变定义了稀疏/欠采样权衡曲线的尖锐边界(13) ; 特别是，当模型的复杂性增加超过阈值时，模型选择和拟合突然中断，这取决于数据大小和真实复杂度。对于变量或特征选择，这限制了数据分析的成功程度。数据驱动的特征选择是惩罚方法的特性，惩罚方法根据特征的预测能力来选择特征，从而限制了模型中特征的数量。

3.2.3 特征工程

理论上有趣的特征，例如，累积风险（两个预测因子的乘数效应）或测量之间的变化（例如随着时间的推移体重减轻），不能简单地添加到变量池中以完成检测任务。需要根据领域知识设计特征，例如，构建差异度量（difference measures）或平方项（squared terms）。最近提出了一种研究系统特征交互的方法，即基于树的随机森林特征重要性和特征交互网络分析框架（15）。本文还建议探讨（相关）自变量集合中复杂性的降低是否有意义，例如基于理论的因素分析或数据聚类或变量选择，以提高特征的比例，并且针对具体的研究领域和方法规范提出了样本规模的建议(16)。如果数据集足够大，一个常规经验就是数万个相关单元（例如，一个调查的受访者）即可用；这使得神经网络的使用成为可能，众所周知，神经网络使用特征工程来生成模型。

虽然有必要保证连续变量具有等效方差，但使用手工特征工程局限于社会和健康科学的研究人员确保现实世界应用中的一些可解释性，特别是在需要明确现象定义以便在现实世界干预的情况下进行因果推断(17)。假设我们反复评估身体质量指数（Body mass index, BMI）来预测或解释健康状况，评估时标记 BMI 的模型为 No.x（或疾病发作前 x 年），这在实践中可能没有意义; 然而，在手动特征工程后，作为疾病预测的模型标记BMI的增加或减少可能对识别高危患者非常有用。另一方面，传统的建模高度依赖于研究人员的决策（例如，建立二次关系而不是线性关系的模型以及手动建立交互效应的模型），如神经网络的基于算法的决策关于特征工程可以提供更稳健和准确的发现。

3.3 模型建立

在建模过程中，机器学习方法通常包括三个步骤: (i)训练、(ii)验证和(iii)测试。大多数研究人员都熟悉机器学习建模过程，其中包括首先将数据分割成一个训练和一个独立的测试集，然后进一步将训练数据分割成训练集和验证集。

（1）训练：在训练集中估计模型参数。

（2）验证：利用验证集评估已训练的模型以选择最接近相关指标（如复杂度）的模型，并调整最适合的超参数。

（3）测试：该模型在一个单独的（保留的）测试数据集上进行测试，以评估其泛化误差。这个测量结果表明了该模型在未来的数据集上的性能表现，例如分类的准确性。

为了提升验证集和测试集上的性能，可以采用交叉验证的方法。该方法同样被应用于传统的统计方法中。

研究人员需要注意高准确率与过拟合之间的权衡。由于过拟合，训练误差通常随模型复杂度的增加而减小。测试误差曲线呈 U 形，先由于过拟合而减小，而后由于过拟合而增大（如图1所示）。

模型误差和复杂度之前权衡的示意图

虽然这种情况具有最小测试误差，但一定不要使用测试数据进行模型拟合或选择模型，否则将得到一个过于乐观且不切实际的性能测量值。因此，在验证阶段，训练数据更进一步地被划分为验证集，并且模型复杂度和调参是在最小化验证集误差时完成的。为了提升估计准确度并降低方差，通常在K折数据集上进行交叉验证。然而，在测试中也可以进行交叉验证以改善对测试误差的估计，特别是在样本量较小的情况下。为了确保测试数据没有经过训练，可能需要嵌套K次的操作，即使用K折验证来选择每个测试内的模型。此外，如果使用交叉验证得到的测试误差，则应该指明随机划分的重复性，以允许其他研究人员进行比较和测试。图1说明了预测准确性和过拟合之间的权衡，突出了训练、验证和测试误差之间的相互关系。我们总是期望训练误差曲线低于测试误差曲线，这是因为大多数方法的目标是最小化训练误差。验证误差曲线通常位于测试误差曲线之上，因为它是在较小的训练集上进行训练的，而且由于数据随机划分，验证误差曲线也可能具有高度的可变性，尽管交叉验证有助于减少这种可变性。然而，验证的目标是确定模型的灵活性，即测试误差的最小点。注意到，在假设数据是独立且分布相同的情况下，交叉验证是合适的，但对于某些数据，例如时间序列或纵向数据，这是不合适的，必须考虑到数据的结构。当验证曲线相对平坦时，最好使用更简单的模型。

在模型建立阶段，许多预测机器学习方法会给特征（变量）分配重要性，以更实质性地提高性能。社会和健康科学的研究人员需要意识到，一些机器学习方法，例如回归树，仅仅因为有更多可能的分裂点，就会高估连续预测的值。虽然在某些算法中存在分割分类变量决策的规则，但它们在不同软件包之间的处理方式是不同的。相比之下，如BART（在下面更详细地描述）这样的方法应该同时处理连续、二分和分类预测的问题。经验表明，连续变量可能仍然受到青睐。

模型建立可以通过友好的用户界面来完成，这些界面是在过去十年中开发的。AutoML 方法旨在促进非数据科学研究人员应用机器学习(19)。默认情况下，AutoML 对广义线性模型、梯度提升机Gradient Boosting Machine、随机森林和深度神经网络进行训练和交叉验证，并通过超学习（SuperLearning）或集成结合模型以改进拟合效果。Python的软件库scikit-learn 允许研究人员通过一个用户友好的平台来选择机器学习算法(20)。虽然易于使用的界面对非数据科学研究人员具有吸引力，并且在许多情况下可能有帮助，但是我们仍然认为，与传统推断统计学的研究类似，对应用方法更详细的理解对实质性的研究是有贡献的。

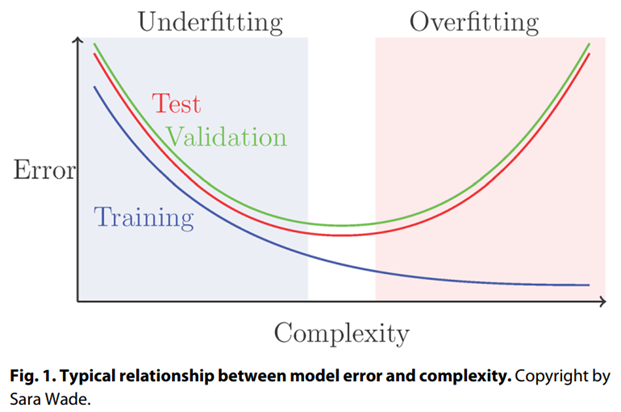
3.4 真实世界应用机器学习的考虑

在机器学习基础上开发的模型，类似于更“传统”的模型，能够在社会和健康科学的政策和实践中告知预防、诊断、治疗和护理。利益相关者、用户以及整个社会都需要接受机器学习在现实世界中的应用。简而言之，机器学习（在这种情况下通常被称为人工智能）需要“值得信赖”。特别相关的是，当为机器学习驱动的医疗保健或社会应用建立更大的框架时，需要保证机器学习和人工智能在技术和社会的角度都是合法的、道德的以及强大的(21)。我们建议读者参考最近出版物中关于“可信赖的人工智能”的讨论(21)。在接下来的文章中，当我们将机器学习应用于社会和健康科学时，我们将参考三个相关的可信赖人工智能的概念，特别是(i)可解释性、(ii)公平性、(iii)普遍性以及(iv)机器学习来辅助人类的能力和技能。

3.4.1 可解释性与可视化

可解释的机器学习意味着从机器学习模型中提取相关知识，例如，能够输入学科领域知识，并拥有预测准确度、描述准确性和相关性等属性，其中相关性是相对于人类受众进行判断的(9)。可解释性在高风险决策中尤为重要，例如临床决策。不同于寻找原始“黑盒”模型的可解释性，部分学者提出需要设计可解释模型，因为只有可解释模型才能实现用户眼中的透明度和可信度(22)。可解释的人工智能在更近期的项目中通常被称为可解释的人工智能（explainable AI, XAI）(23)。

在实践中，可解释性常常与可视化变量之间预估或找到的关系有关。为了提高可解释性，通过潜在的非线性模式或非随机缺失的数据，可以可视化二变量和高阶数据的关联，例如部分依赖图（partial dependence plots ）(24)、SHAP图（Shapley Additive exPlanations, SHAP）(25,26)或个体条件期望图（individual conditional expectation plots），也被称为适应部分依赖性图（adaptation of partial dependence plots）(27)。

3.4.2 公平性

在健康和社会科学中，一个概念是机器学习算法要“公平”地决定，即不歧视某个社会或少数群体。本文参考了其他文献中与ML中的公平性有关的例子(28)以及一个卫生保健算法中种族偏见的突出例子(29)。在这里，特别是在机器学习在高风险决策（如预测累犯）中的应用中，需要平衡模型的预测准确性与所有社会群体公平性，即机器学习模型中所有社会群体获得理想结果的概率相等。重要的是，结构性歧视/种族主义会无意中破坏机器学习决策中的健康公平。这种“算法公平”的概念受到了批评。解决“在数据中”产生公平问题的新方法建议定义反事实公平(30)。最近的一项系统评估表明，使用公平标准会损害模型的性能，同时也会导致公平性方面有争议的改进(31)。因此，研究人员建议考虑更广泛的社会技术背景(31)，虽然这可能破坏算法之外的公平性。在我们的研究范围之外，要认识到公平性不仅在算法的应用中很重要，而且在整个研究过程中也很重要。从公平的研究问题、公平的数据收集、公平的数据分析到机器学习算法的部署后评估的这一流程，已经被定义为验证决策算法的“公平性”(8)。数据不平等，即生物医学保健研究领域中少数群体成员的小或低质量的样本可以被解决：训练多数群体数据，而后使用（知识）迁移学习来微调模型在少数群体数据中的表现(11)。然而，除非卫生保健数据中的数据不平等得到系统的改善(11)，这仍然存在着一些问题。

3.4.3 泛化性或者外部有效性

外部有效的泛化能力的重要性不仅限于ML方法：在研究设计和数据收集的各个阶段，因为希望研究结果的有效性超出发现它们的数据集，都需要考虑可能损害泛化性的偏差。在 ML的背景下，考虑过度拟合的风险是重要的，即通过未使用数据集的模型性能风险提高数据集内模型的准确性。

一个招募差异如何导致ML算法性能差异的例子是（32）。此外，与更传统的分析类似，建议对方法进行三角测量。本文进一步强调在统计分析中记录所有决策的重要性（例如，指定随机数种子），以确保科学发现是可复制的。

泛化性的一个特殊情况是关于测量的假设，即因素或自变量与感兴趣的结果或因变量是静止的，即不随时间变化，也不取决于模型的输入。然而，在许多情况下，需要意识到潜在的漂移，即由于外部因素而导致的输入与输出间关系的变化。这与不断接收新传入数据进行处理的ML引擎相关，这些数据可以利用医疗保健、教育或消费者数据进行设置（尽管在撰写本文时，在社会和健康科学研究中并不广泛可用）。随时间漂移的一个例子是，当贫穷的社会决定因素随时间变化时，贫困解释儿童健康的预测能力降低，请参阅（33）中的无障碍介绍和（34）中的最新发展。虽然迄今为止社会和健康科学的大多数研究都涉及静态数据集，但随着不断实时在线ML 引擎的开发，如跟踪应用程序或社交网络数据，这一概念的重要性将增加。

3.4.4 提升人类能力和技能

有许多 ML 可以在工作或日常生活中支持人类。推荐系统应用于多个领域，根据先前的信息（例如相同或其他用户的评级）向用户推荐相关项目。从在旅游、商业和营销中对推荐系统的使用，本文只是举例说明推荐系统如何帮助工作和医疗保健：推荐系统可用于克服咨询师与自杀预防热线可以帮助作家在顾问长时间聊天中的障碍。该方法有望帮助情感上有困难者，即便此时人类专家的表现仍然超过推荐系统（35）。我们现在转向用于描述、预测和因果推理的 ML 方法的分类（其中一些是公认的起源于标准的统计方法），并从描述用于描述的ML方法开始。

4. 描述中的机器学习

一个描述性的研究问题旨在“对世界的某些特征提供一个定量的总结”（6）。描述是所有应用研究的基础，因为我们需要描述来量化所研究的现象，例如，评估（社会）群体、国家或地理实体的普遍性或分布变量以及其随时间（队列之间）的变化。这可以通过几种算法完成（如表1）。在转向社会和健康科学的研究目标与描述之前，我们首先介绍两类相关的方法，即因子和聚类分析，社会和健康科学的许多研究人员已经意识到了这一点。

表1 综述与社会和健康科学中最相关的机器学习方法非技术描述

用于描述的机器学习

聚类

聚类可识别数据中的相似结构，并根据与距离、密度相关的特定标准，以及聚集较小群体或划分较大群体的策略，将与以前未知的聚类相似的对象分组。例子如下: 1）K-means：根据n维空间中的距离度量对数据点进行聚类 2）层次聚类：从每个对象形成一个单独的集群开始，向上依次合并形成集群。 3）基于模型的聚类：最广泛的应用的是高斯混合模型（Gaussian mixture model, GMM），它允许通过椭圆形聚类。 4）基于密度的聚类方法(DBSCAN)(131,132)将空间邻近的数据点分为一组，同时将低密度区域中的数据点标记为异常值。 5）专家（学习者）混合：该方法将输入空间划分为同质区域，每个区域由不同的专家负责。该方法允许不同的集群，例如患者在y和x之间具有不同的 (非) 线性关系(133,134)。

降维

1）主成分分析：社会和健康科学的研究人员已经知道，该方法通过线性 (正交) 投影提供数据的低维近似/编码 (即低维特征是原始特征的线性组合)。 2）概率主成分分析 (PPCA) : 用于代谢组学中发现的高维数据的主成分分析的概率模型公式。PPCA可以为PCA的零噪声(135)限制下提供解决方案。 3）因子分析: 正如社会和健康科学的研究人员所知，，如基于调查问卷的数据分析过程中，因子分析可以被视为一个允许维特定噪声的广义PPCA。该方法通过少量的潜在因素来解释维度之间的相关性。 4）独立成分分析：因子分析的推广，允许潜在因子的分布为任意非高斯分布。 5）非线性降维：包含核PCA、高斯过程隐变量模型和t-SNE。 6）生成式对抗网络：基于数据相似性聚类的任务分为两步：首先，生成真实数据相似的新数据；其次，类似于有监督学习，区分数据是真实还是新（假）数据。一旦算法不能区分真实数据和新数据，任务就会停止(136)。 7）变分自编码器：使用神经网络进行降维，包括编码和解码（将数据映射到低维潜在空间，反之亦然）。VAE使用概率公式和变分推理来学习潜在变量的分布，这样可以避免过拟合，并在潜在空间上增加理想的属性(137)。

异常检测

这是一个识别偏离正常“行为”数据点的过程，即在整个数据点的背景中识别不同的数据点。异常值可能表明一个事件的越轨行为（例如，消费数据中的欺骗银行转账数据或消费者家庭组成的变化）。异常检测可以是社交网络分析的一种特殊形式（见下文）。

双聚类

作为一个较新的发展，人们也可能会对同时聚类样本（个体）和特征（变量）感兴趣。所谓的双聚类方法同时对样本和特征进行聚类；有关的最新综述，请参见(138)。双聚类用于生物信息学，例如根据基因子集上的表达谱对患者进行聚类(139)。

社交网络分析

SNA可用于评估不同的数据点（节点；如用户、选民、同事和组织）之间的连接或关系（边）。SNA用结构或基于内容的度量来描述网络，如(53)所述。结构测量的例子是中心性，其能评估网络中节点的相关性或结构重要性，并可将中心性测量推广到一组节点，如度中心性（连接更多的节点排名更高）、特征向量中心性（调整邻居的重要性）或群体中心性。此外，再次不同的评估是可能的，如群体度中心性。基于内容的分析可以提取用户画像或会话主题。

降维可以降低数据集的复杂度，以便后续进行更有效的分析。因子分析将为所包含的变量提供因子和因子载荷（factor loading）。在后续的分析中，因子通常被用作富集后信息的变量。读者应该注意到，基于贝叶斯建模的算法可用于因子分析和本文所介绍的其他方法，但本文不会详细介绍。领域知识对于预选可解释和有意义的因素分析变量是必要的，因为聚类（和因子）分析不能从概念上区分变量，例如数据来自人类或其他的情况。此外，不建议将个体变量与高阶变量混合，以确保后续分析中因子的可解释性，例如在因子分析中与环境或邻近地区相关。另一个有用的数据聚类是根据相似性对数据进行分组。与因子分析不同，数据聚类可以同时帮助应对个体水平和背景水平中变量的测量。例如，个体层次的BMI和背景层次的空气污染，以调查心血管死亡率的不同风险组或概况（例如高BMI和高空气污染）。最后，如果样本和变量需要同时分组，双聚类可能会有所帮助。

描述性研究目标可以在众多社会和健康科学中被发现：包括(i)筛查和识别高危个体或更高水平的模式、(ii)识别风险概况、(iii)不良结果患病率进行估计和预测以及(iv)诊断的研究目标。这四个研究目标将在本节的其余部分中描述。

4.1 筛选和识别高危人群或更高层次的模式

可以通过数据的自动化处理对个人进行逐一的风险因素筛选。例如，可以通过处理电子健康记录来确定不良健康结果风险较高的人。这个研究目标可以用异常检测的算法来完成。通过聚类或因子分析，可以分析个体之间的模式，并同时分析一组变量。为了确定与衰老相关的发病情况，使用不同的聚类算法对包含278种高负担（ high-burden）疾病信息的电子健康记录进行分析，以根据疾病发病时的年龄对疾病进行分组(37)。另外，从ML得到的复杂信息可以通过传统的画图进行可视化，如每个疾病簇的疾病曲线的分布(37)。

对时变变量轨迹的纵向分析可能有助于更好地了解以前确定的危险因素的短期或长期变化，最好是至少有五个随访测量。许多社会和健康现象在一生中都会发生变化，其轨迹可以被认为是正常的发展（例如，在儿童和青少年时期认知能力的提高，在晚年时期认知能力的下降）。然而，其他变化可以预测疾病（例如，强烈的体重增加，强烈的体重减轻，或中年认知能力下降），因此这与干预和实践相关。在需要持续监测和干预的情况下，短期重复评估可能是相关的，例如在手术背景下(38) ，监测因素的轨迹可能会带来对患者状态的额外理解。在长期风险预测相关的疾病中、或者在前期需要区分因素是否为危险因素中、或在早期症状的情况下，长期重复评估可能是有趣的。在长期监测中，通过抑郁症状数量的K-means算法来识别每个测量场合的抑郁轨迹，以区分早发型抑郁症和晚发型抑郁症，并测试它们与不良大脑结果的关联(39)。另一项研究通过模糊聚类首发精神病患者的数据来确定“优良预后”、“缓解过程”、“临床恶化”和“慢性过程”的四种轨迹，其中有不同的恶化和缓解过程的危险因素。类似的分析可以帮助强调不断变化风险因素的重要性及其在生命过程中的相互作用。

死亡作为一种具有竞争性的风险需要在老龄化相关疾病的调查中加以考虑，例如随机存活森林。该方法同样可以对时变风险因素进行建模(41)。如果重点是时变治疗的短期后果，即希望得到因果结论，那么在潜在结果框架中使用已建立的方法（如边际结构模型或 g 公式）效果更好(42)。

4.2 识别风险状况

为了识别风险的属性，即识别一组个体对一组变量的特定值，可以基于以前已经识别出风险或保护因子的文献，采用发现机器学习来描述并降低复杂度。通过使用重症监护室环境中常见的严重程度评分，患者健康状况轨迹可用时间序列数据中的多种降维（和预测）技术进行分类，包括基于密度的聚类算法（DBSCAN）(43)。这些健康状态轨迹与药物和治疗相关，但其结果模式的可视化是值得肯定的 (43)。

虽然社会和健康科学中的大多数描述性研究问题都需要无监督的机器学习，但对于无监督的机器学习来说，描述问题中不存在一对一的双射。接下来将介绍需要有监督机器学习方法进行预测的描述性研究问题。

4.3 估算和预测社会或健康结果的普遍性

估计疾病流行率是量化卫生负担、干预需求以及规划卫生和社会保健未来的基础。估计所研究现象的发生率、发病率或流行率，例如特定人群中的健康结果，如糖尿病，可以被认为是描述性的。估计的预测更倾向于预测性的。举一个纳入健康视角的社会决定因素例子。根据年龄、性别和种族/民族对非传染性疾病（NCD）的流行率进行估计（可通过个体层面的数据或汇总数据），而后通过ML估计未知地区的流行率。通过LASSO估计了6种非传染性疾病的存在，并以最小的人口统计数据集预测了美国5个州(44)的非传染性疾病流行率。不同地，Wang和Rodriguez (45)使用对数线性模型对空间随机效应作为广义模糊LASSO（generalized fussed LASSO）的惩罚函数，以确定空间疾病簇，即发生率高于预期的地区。在这种情况下，儿科癌症在佛罗里达州有较高的发病率。另一项研究使用循环神经网络，更具体地说是长期短期记忆和门控循环单元网络来监测疾病活动。在这种情况下，在美国流感疾病爆发有多种空间分辨率(46)。

4.4 诊断

描述性研究的目标是确定一个社会或健康结果的流行率。与健康状况有关的诊断通常也可以在没有临床评估的情况下进行合理推断，而临床评估的指标是疾病指标（例如，糖尿病的高血糖）。根据现有的信息，推断出的诊断可以被称为“可能”。在接下来的文章中，我们将介绍以下目标: (1)评估可能的诊断、(2)解决报告不足或诊断不足、以及(3)通过网络识别和传播社会或文化影响。

4.4.1 获取可能的诊断

由于资源缺乏或数据隐私的问题，在数据稀缺的环境中，个体（受访者）疾病的描述和识别目标可能是相关的。如果分析的数据包含有标签的和无标签的，则任务可以通过有监督的机器学习或半监督来实现。通过使用电子健康记录的数据，如神经网络等算法可以在没有人类临床评估的情况下，识别致病的特征的存在（或联合存在的条件）。其他数据，如传感器数据和语言数据，则可以通过本文未涉及的方法来检测条件或疾病，如自然语言处理。许多其他应用已经被用于检测社交网络数据中的抑郁症(47)。

在缺乏基于临床评估诊断的情况下，通过ML对潜在患病的个体进行分类可有助于估计疾病流行率和相关的医疗保健费用。虽然确定潜在患病个体是不引人注目的，但比对这些个体进行临床评估更具成本效益。结合主成分分析和数据聚类分析，研究人员利用世界各地的数据集对痴呆可能性高的参与者进行了鉴定。通过文化和教育公平的认知测试，将ML应用于来自南印度的数据(49)，10/66的痴呆诊断可以在没有临床评估的情况下通过认知测试。

4.4.2 解决报告不足或诊断不足的问题

对个体的潜在诊断进行补充分类，可以解决痴呆等疾病的报告不足和诊断不足的问题。这些个体水平的可能诊断可用于调查这些条件的风险和保护因素。通过使用传统算法和ML（描述性和预测性）算法的混合算法，调查参与者可能被确诊为痴呆。该算法的目标是在种族/民族群体中提供具有相似敏感性/特异性的痴呆分类算法(50)。这项研究证明相比于传统的专家建模，即基于领域知识的特征选择，机器学习的实施更为复杂且对队列和研究程序差异更敏感; 此外，在这种情况下，使用LASSO和超级学习器等机器学习方法，与不同的专家模型相比，没有带来模型性能的增加(50)。因此，对于机器学习方法的使用，可能不太推荐使用时间跨度较长的不到2000名参与者的样本。

4.5 识别和传播社会或文化的影响

一个与诊断相关的特别的研究问题可能是在网络中识别和传播社会或文化影响，这可以用社交网络分析（social network analysis, SNA）来解决。在多项实证研究中，本文选择几个例子以说明SNA如何成为社会和健康科学中经典统计分析的有用工具，并可用于分析社社交网络和信仰中政治态度传播的决定因素，以及组织内部和组织之间的合作。

在SNA的框架下，已经开发了特定的ML方法，如指数族随机图模型(51)，但是我们发现许多用预测的ML方法进行SNA的例子，如支持向量机或深度学习 (见表2)。SNA已经被用于衡量政治倾向，并可通过基于上下文的分析来识别用户档案和对话主题。Barberá 等人的研究是利用这两种方法来理解在社交媒体上（低于预期的）政治倾向。SNA的概述以及评估可以分为的四个不同维度，即模式和知识发现、信息融合和集成、可伸缩性和可视化，详见(53)。应用于SNA的基于上下文的ML方法可以评估其性能，类似于在预测上下文中的应用，例如关于准确性或精确性(表4)。在接下来的小节中，我们将描述用于预测的机器学习方法。

表2 综述与社会和健康科学中最相关的机器学习方法非技术描述

用于预测的机器学习

回归

1）线性回归: 通过将截距加入预测因子及其估计的加权和中来预测连续的结果，最常用的方法是使预测误差的平方一般最小平方法最小化。 2）逻辑回归: 预测分类结果的可能性，使用逻辑函数作为广义线性模式中的连接，是最常用的符合最大可能性或梯度下降法，并且可以扩展到反映两个以上的结果类别。

人工神经网络和深度学习

人工神经网络通过大量的数据点（变量和个体）来搜索复杂的数据模式，建立连接单元或节点，并模仿简化大脑结构的相互连接的神经元。 1）卷积神经网络：对较小的网格数据单元（如成像或序列数据）应用过滤器，并将相应的激活转化为特征映射，但计算代价高且数据量大，性能优于需要人工特征定义和图像分割的传统的成像分析方法。 2）多层感知机：最重要的人工神经网络由一个输入层、至少一个隐含层以及一个输出层组成。每一层的神经元包含前一层神经元的加权汇总，并用激活函数计算，通过反向传播描述了如何调整权重的过程，以尽可能地减小输出层的误差。

集成方法

1）随机森林：基于输入变量的随机子集，将自引导概念应用到个体决策树中，根据个体决策树生成的森林投票得到结果。 2）XGBoost：梯度提升机的软件和硬件优化实现，使单个决策树的顺序组合的预测误差最小，性能优于随机森林，特别适合结构化的表格数据。 3）贝叶斯加性回归树：在贝叶斯框架中嵌入单个决策树的顺序集合，允许度量估计值的不确定性，设置统计的鲁棒默认，因此不需要手动正则化或调整超参数，也可以用于因果推理。 4）超级学习器：使用多种描述和预测的ML算法，并通过交叉验证估计各自的性能。超级学习器的准确性接近最佳预测算法。

支持向量机

支持向量机（SVM）一直是分类或回归中最广泛使用的监督学习方法之一（140）。SVM通过寻找数据点（向量）之间的超平面来训练模型，并选择最能够将一个类别的数据点与另一个类别的数据点分开的超平面（即具有最大的余量），也就是超平面与每个类别的数据点的距离是最大的。即使在近年来被梯度优化和其他集成算法（141）超越，SVM仍然是稳健的预测方法。

正则化算法

1) 岭回归：在似然之和（最大似然）或平方之和中加入一个基于回归系数的正则化项 残差（普通最小二乘法），可以减小大型模型方差的偏差，即缩小了参数，可应用于线性或逻辑回归。当大多数变量是有信息时，算法表现良好。 2) LASSO：类似于岭回归，对变量选择很有用，因为其可以将非信息变量的估计值缩减为0，而岭回归只能渐进地将估计值向0收缩。当许多变量为非信息变量时，算法表现良好。 3）弹性网：引入了基于LASSO和岭回归的正则化。当变量相互关联并且未知变量信息量大时，算法性能表现良好。

决策树

1）分类和回归树（CART）：单个决策树。数据根据分割点或切割点被反复分割成不重叠的仓。这些仓指的是用贪婪算法确定的预测器值。预测是基于通过遍历树中各自路径到达的终端/叶子节点的平均值或多数票。随机森林等基础元素。 2）条件推理树：与CART类似。递归分区的变量选择是基于显著性检验，而CART是根据信息最大化措施（如基尼系数）来选择分割变量，基尼系数是收入不平等研究中经常使用的统计离散性的衡量标准。

5. 预测中的机器学习

预测问题在社会和健康科学中高度相关：我们可能希望某个预测，即社会或健康的结果，要么尽可能准确，要么尽可能简明。研究目标可能是解释结果中的最大方差，或者找到最小或最优的预测因子集，以改善对高危人群的识别。也可能想评估某个如潜在风险因素的输入，能够多好地预测结果。预后的最简单形式是预测。可能有确定的终点，我们希望估计达到其中一个终点的概率。从ML的角度来看，让计算机/算法代替人类来定义模型，ML可以通过考虑一大批变量来测试一个或多个预测因子的相对重要性，并提供因子重要性或排序信息。此外，前文提到的“维度诅咒”也同样适用。如果想要更为深入的解释，可以参考预测学教科书（12）。

预测的研究目标需要将一些特征（输入）尽可能准确地映射到其他已知的特征（输出）上（6）。同样，如健康结果等已知结果，被称为有标签数据。因此，在预测问题中使用有监督学习。如上所述，有监督学习是指从有标签的数据中学习一个函数，将“输入”（预测因素和自变量）映射到“输出”（结果）的ML任务。数值（连续）结果需要回归技术，而二分或分类则需要分类技术。图2介绍了ML方法的概况，在考虑理论和经验的基础上，对这些方法的可解释性与复杂性之间的权衡进行了排序。在介绍社会和健康科学中专门针对预测的研究问题之前，本节对通常提到的用于预测的常见ML方法进行了概述。

机器学习方法用于预测社会和健康科学的非技术描述，按可解释性/可解释性与复杂性进行排序。

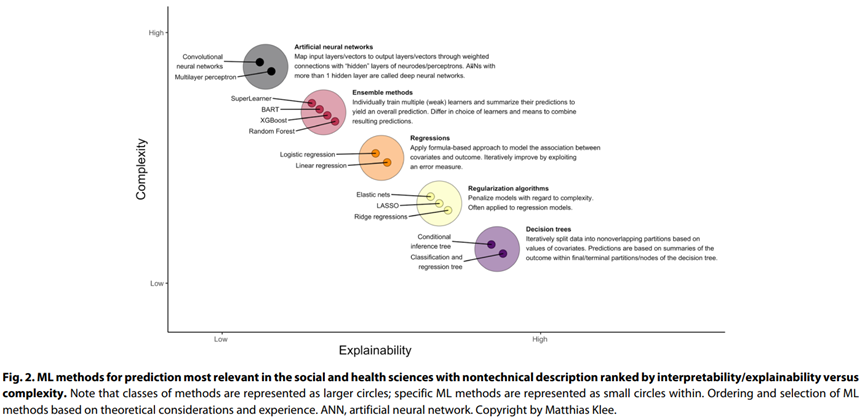
5.1 常见的预测性机器学习方法

作为少数流行的或表现良好的ML方法，解决预测问题的典型ML方法有：（i）惩罚性方法、（ii）集合学习以及（iii）神经网络，下面将对这些方法进行更详细的技术描述，更多的方法如表2所示。

5.1.1 惩罚性的方法

缩减或惩罚性回归方法也被用于传统的推理统计中。惩罚性回归在大型多变量数据集中表现得比标准线性模型更好，是因为这些数据集的变量比个体更多。惩罚性回归将在方程中添加一个约束条件，以惩罚模型中变量过多的线性回归模型，也称为“收缩”或“正则化”。这将使系数值向零缩减，进而导致贡献较少的变量的系数将接近零或等于零（4）。最广泛使用的惩罚方法，对应于不同的收缩惩罚，包括LASSO、岭回归和弹性网。然而，虽然LASSO将一些系数设为零，从而同时进行变量选择和估计，但其存在着众所周知的估计偏差。为了克服这个问题，人们设计了包括平滑剪切的绝对偏差（54）的其他惩罚措施。此外，还提出了考虑数据结构的各种扩展，如用于时间结构变量（或更普遍的图结构变量）的fussed LASSO和用于组结构变量的group LASSO。

5.1.2 集成学习

下面将介绍常见的集成学习算法，包含随机森林、XGBoost和超级学习器。BART也是一种集成学习算法，但其相关软件包提供了许多基于领域知识的因果分析设置（55，56），因此常被用于研究因果问题，故将在第六节进行介绍。首先，如随机森林（57）等集成方法以其可解释性已被用于社会和健康科学的许多研究中，如（41，58）。

其次，由于其预测精度高和对许多预测问题的强大适用性，本文向读者介绍随机梯度提升（59）。Python和R中已经实现了梯度提升算法系列的即用型软件包，如推荐中的“XGBoost”软件包。通过提升算法，典型的输入变量（预测因子）的共线性问题就不会出现。这意味着 不同的工程（预处理）变量可以同时输入，以寻找最具预测性的特征。研究人员需要注意的是，该算法会在所有变量上详尽地搜索以寻找分割点，并且在划分样本时有些变量可能比其他变量更有参考价值。因此，该算法偏向于选择数值的（连续的）、多类别的变量或有缺失数据的变量而不是二分法变量。该算法可以进行无偏的变量选择（60）。此外，那些最能解释因变量的变量将被选为分割点，但从社会和健康科学的相关理论角度来看，这不一定是最有意义的理论变量。

最后，一些集成学习算法测试了跨多个ML算法开发的模型性能的可能性。算法家族中的一个例子是超级学习器，其已被应用于流行病学研究问题（61）。超级学习器使用交叉验证来估计几个描述性和预测性ML模型的性能，或者在同一模型中使用不同的设置参数，并且在模型拟合过程中与使用的最佳预测算法一样地逼近准确值。一个这方面的应用是缺失数据的补全（62）。

5.1.3 人工神经网络

人工神经网络通常利用大量的数据来搜索复杂的模式并建立连接单元或节点。具有一个以上隐藏层的人工神经网络也被称为深度学习。

人工神经网络详细的描述：通过将一些特征（预测因子）映射到其他特征（结果）来解决预测问题的一种更复杂的方法可以用神经网络来完成，其具有定义的输入（预测因素）和 输出（结果），并学习变量间的相互关系。神经网络是受大脑中的计算为驱动，并使复杂任务的成功识别和分类成为可能（63）。如果采用最常见的逻辑激活函数（64），神经网络与没有隐含层的传统逻辑回归是一样的。神经网络和逻辑回归都有一个函数形式，并且参数是由最大似然估计确定的。然而，神经网络允许模型放宽关于输入变量线性和对数几率的假设。因此，如果数据不是线性可分的，神经网络是一个更好的选择。但这种灵活性是以难以解释参数作为代价的。其所产生的模型是通过性能指标来评估的，如敏感性、特异性、准确度以及接收者操作特征曲线下的面积（见表4）。神经网络在输入和输出之间建立了至少一个隐藏层，而神经网络提高模型性能的好处实际上来自于算法中多个隐藏层的能力。神经网络的训练过程主要包括两个步骤：首先，前向传播将输入层或其之后隐藏层的权重相结合。而后，反向传播将输出层或其之前的隐藏层在实际值和预测值的误差基础上进行调整。通过这种前馈和反向传播的迭代，神经网络训练以适应传递和回归参数。如果训练后没有认真地测试和交叉验证，那么神经网络很容易出现过拟合的情况。正则化可以通过交叉验证或bootstrapping来解决这个问题（65）。

另一种方法是使用贝叶斯框架。该算法给出计算参数的分布，而非一个点的估计，以避免过拟合问题（66）。此外，虽然神经网络倾向于过度自信，即预测可能是错误的并且容易受到对抗性攻击(67)，而贝叶斯神经网络，它产生了一个神经网络的集合，是稳健和准确的（68）。这对于提高社会和健康科学的信任度和社会接受度可能特别有意义，因为其考虑了算法和结果模型的复杂性与可解释性的均衡。

本文接下来将介绍与预测有关的研究问题以及来自社会和健康科学的例子，特别是(i)社会或健康结果的预测、(ii)识别和评估风险因素以及(iii)识别过程和偏离“正常”的情况。

5.2 预测社会或健康的输出

很多时候，理解一种社会现象或疾病的第一步是同时考虑到社会人口、心理、健康、教育或其他相关的决定因素（预测因素），并预测谁会显示出结果。我们首先讨论(i)输出，即预测一个通常是不利的、但有时对于某些研究问题也是有益的社会或健康结果。然后，转向寻找 (ii)最小或最佳的预测器集以及(iii)对罕见结果的预测提出改进建议等研究目标。

5.2.1 预测不良结果的准确性

预测不良后果的模型建立通常包含在研究人员选择的大型特征集上进行训练。可能的 模型性能的改进应通过建立额外的模型、添加更多的信息（变量）、或者考虑高阶相互作用的或非线性的模型。典型的研究问题是测试与传统建模相比，ML带来的预测准确性改善，如关于健康的社会决定因素（58）、对痴呆症的预测（41）以及糖尿病和糖尿病并发症（69）的预测。通常基于ML的模型不会明显优于传统的基于回归的模型。但是，其他研究表明，可以用长短期记忆递归神经网络通过电子医疗记录来估计病人的剩余预期寿命。剩余寿命是面向病人的衡量标准，可用于及时启动预先护理（临终）计划（70）。这个研究的一个很好的例证是对退伍军人自杀的预测。在与当时活着的1%随机匹配的退伍军人数据集的测试中，BART是几种ML算法中最好的一种（71）。其他的研究使用了超级学习器进行死亡风险预测（72）。一项关于用ML进行临床风险预测的系统发现，ML方法比回归算法的提升不明显，并且批评了迄今为止文献中的一些缺陷，特别是缺乏校准，即测试预测的可靠性（73）。研究人员可能意识到，预测因素越远，越难达到稳健的、准确的预测结果。举一个例子，一项研究使用惩教设施的特点和囚犯的总体特征来预测监狱暴力并用囚犯间的攻击次数进行评估，但超级学习者未能达到很高的准确率（74）。社会地理学中的空间映射同样被证明是可用的。例如，一项研究使用手机数据绘制了贫困和财富的地理分布图，并得出了与实地调查数据类似的分布（75）。

在临床实践中，相关的输出可能并不是不利的健康结果，而是干预的必要性和最佳时机。对临床决策的最佳时机的预测已经被研究过了。例如，van der Schaar实验室已经开发了自动ML架构，并称为AutoPrognosis，以预测不利的心血管疾病结果，且其性能优于比传统的风险评分(76)。

5.2.2 社会或健康结果的最小和最佳预测器组

社会或健康的输出也可能是希望找到一个最小或最佳（最简明）的预测器集合。回到前面提到的预测非传染性疾病的人口水平流行率的例子，这些疾病是用最小的社会人口学预测器组来估计的（44）。在痴呆症风险预测方面，至今仍没有强有力的算法。最近用LASSO开发了一个预测10年以上痴呆症的最佳模型（77）。另一项研究组合LASSO和随机森林算法，以寻求一个最佳的预测器组来解释枪支暴力的差异（78）。

5.2.3 罕见结果预测

健康和社会科学中的一个典型问题是预测罕见的事件，如疾病、犯罪、学习困难和离婚。在这种情况下，只有非常小比例的被观察人口会出现感兴趣的结果。例如，与总人口相比，犯罪者的占比非常小；自闭症只在2%左右的儿童中流行；多达三分之一的已婚人士会提出离婚。通过ML来预测罕见的结果（而罕见可以定义为任何概率低于50%的案例），分类算法通常会简单地开发一个模型，该模型只预测不发生的结果，因为算法会检测到在大多数情况下，“0”的猜测是正确的。研究人员可以通过几种策略解决这个问题。

1）重新定义结果。例如，转化为一个回归问题而不是分类问题，例如，使用抑郁量表的全部范围作为连续或泊松分布的变量。而不是中度/重度抑郁症临床相关的二元（和罕见的）分类。

2）通过对具有罕见结果的群体进行超额抽样来改变样本中的结果分布，例如合成少数人超额抽样技术(79)是很好的方法。同样地，对没有结果的群体进行下采样（欠采样）也是可以的。举一个高度不平衡的金融服务消费者行为的例子，抵押贷款违约的预测和高风险消费者的识别分别对银行和贷款公司来说是至关重要的。最近的一项消费者交易数据的研究对未违约的客户进行了抽样调查，并训练了与随机森林结合的卷积神经网络，该网络结构带来了最高的预测准确性(80)。一些研究报告称，通过对高度不平衡的数据进行重复的随机子抽样可以以预测疾病，并且随机森林的表现优于支持向量机、袋法以及其他方法（81）。应该注意的是，在交叉验证的情况下，采样策略应该被多次重复。从更广泛的意义上讲，需要进行敏感性检查，以便研究不同的抽样策略对性能和可推广性的影响。

3）一个罕见的结果在预选的样本中可能更频繁。例如，痴呆症研究的部分重点是提高从轻度认知障碍（MCI）转化为痴呆症的预测率。只有分析得到的结论不需要在整个人群中成立时，样本选择才能成功，否则这种策略会引入偏见（对结果的条件）。MCI患者的高危样本可以用来训练一个模型，根据问卷调查、生物标志物或基于影像的变量来区分转换者和非转换者。在众多的例子中，一些研究用不同的ML算法测试了认知储备对预测转换为痴呆的作用（82），并在以前未见过的对象中测试了他们用支持向量机算法开发的模型（83）。虽然痴呆风险预测模型有了很大的改善，特别是在向模型中加入遗传和成像信息后，但在预测高危样本的认知性能测试下降的能力方面没有明显进展（84）

4）模拟数据集和 “虚拟队列 “在某些情况下可能是有用的。

5.3 新的或已知风险因素识别和评估

出于对输入的兴趣，即社会或健康结果的预测因素，一些研究利用大型预测器集来确定 识别以前未知的社会或健康结果的预测因素，或在其他变量的背景下评估其预测能力。除了需要考虑维度诅咒外，采用几种ML方法测试以前未测试过的预测因子集可有助于平衡其局限性。以此为目的开展了一系列研究，例如测试与儿童认知表现有关的候选可改变因素（85）。在另一项应用中，梯度提升和SHAP图被用来识别青少年自杀想法和行为的十大风险因素，结果表明这些因素都与社会人口因素以及家庭和同伴关系有关（86）。

一项研究通过可穿戴设备进行的迷你精神状态检查（MMSE）的分数，探究认知功能与已知生活方式的关联（87）。虽然由于研究的横断面性质，无法确定因果关系，但部分依赖图的可视化显示了非线性关联，如关联在某个阈值后趋于平稳，或与反U型关系相关（87）。这样的研究有助于改善对暴露-结果关联中的预期和实际关系的思考，即期望从某种生活方式中获得的益处是持续增加的（线性或二次剂量-反应关系），或者在某一数值后趋于平缓，此后不能再有任何改善（阈值模型）？对这些调查来说，对暴露和结果进行精细的评估是必要的。一项研究用LASSO预测阿片类药物过量的死亡率，发现以前没有发现的相关邻里特征，如居住稳定性、种族/民族分布和社会隔离（88）。另一项研究在横断面设计中测试了童年不良经历与智力的关联（89）。从所选择的术语“风险因素”到更中性的“决定因素”或 “预测因素”，另一项研究旨在通过深度（人工）神经网络检验经典的决策理论（90），利用大规模的风险选择实验，确定人类决策中的驱动因素（预测因素）。

5.4 识别正常过程及其波动

在调查社会和健康结果的轨迹时，研究人员可能希望不仅仅是描述性研究，如果不同的状态或轨迹已经被主题所定义，例如疾病的严重程度或教育或职业水平，则应采用预测性眼光。一项健康索赔数据的研究采用了梯度提升和移动时间窗口方法，调查了最严重的慢性阻塞性肺病和常见疾病轨迹的预测因素。研究员设计了一些诊断（如呼吸衰竭）、药物（如抗胆碱药物）以及与随后的最严重的慢性阻塞性肺病诊断有关的程序（91）。本研究检测到的时间模式更多的是代表了与保健有关的疾病顺序，而不应该在因果关系的意义上进行解释（91）。在其他情况下，检测到的时间模式可能更加稳健。对老龄化过程感兴趣的研究人员希望确定与老龄化相关的社会或健康结果的正常轨迹，并通过梯度提升等方法来确定与正常轨迹的偏差，这可归纳为一个预测问题（92）。研究人员应该意识到，因为定义正常的衰老轨迹并不简单，这个目标对数据提出了极高的要求。理想情况下，需要提供足够的信息以确保可解释性和可复现性。下文将以因果研究为目标描述社会和健康科学的研究。

6. 因果推断中的机器学习

社会和健康科学研究者所追求的大部分都与寻找世界上某一特征的原因或后果有关，故往往会寻求因果问题的答案。如果不仅要找出预测因素，还要找出风险或保护因素，例如，用于某种不利的社会或健康结果的预防。如果不仅想了解决定因素，还想进行干预，那么就需要了解疾病的因果决定因素。

在对因果关系问题找到满意的答案之前，需满足统计分析的多种要求。用于因果推断的ML需要领域知识，即主题知识。根据变量在描述变量之间假定因果关系的有向无环图（DAG）上的位置，合适地选择变量是至关重要的（93，94），这在健康研究中的应用越来越多（95）。任何旨在进行因果推断的统计分析通常会选择那些可以满足因果推断假设的数据集：可交换性（无知性），即对于所有没有接受特定治疗的人来说，如果他们接受了治疗，其结果将与接受治疗的人相同（结果的反事实概率）；积极性，即暴露和混杂因素的每一种值的所有可能值都是可用的，或者在数据集中已经被分配；一致性，即一个人在其观察到的暴露历史下的潜在结果正是他们的观察结果（96）。然而，即便在违反这些条件（有限的）的情况下，如果随机对照试验不满足伦理，或由于其他原因不可行，那么通过定义假设的干预措施或“目标试验”也可以取得一些进展。通过使用具有潜在结果框架的观察性数据，我们可以模仿目标试验（97, 98）。最近的一项模仿目标试验的研究用目标最大似然估计（TMLE）来估计系数，并测试干预可变因素对儿童期BMI反弹的影响（99）。

根据Hernán等人（6）的分类，首先在此考虑用于反事实预测的ML，但本文同时考虑用于因果发现的ML以扩展该框架，即变量之间的因果结构是从数据中学习而来的方法（见表3）。在社会和健康科学领域，结构性因果模型的框架有很大的应用潜力，即便很大程度上还没有被开发出来。

表3 综述与社会和健康科学中最相关的机器学习方法非技术描述

用于因果推断的机器学习

反事实预测

设置数据以满足因果推断的假设，并使用预测性ML（表2）进行效应估计。以下是几个提供了支持因果效应估计命令的软件包： 1）BART：详情见前文描述 2）目标最大似然估计法（TMLE）：在二元点治疗和二元结果的基本设置中，该方法(i)估计接受治疗和未接受治疗的观察值（如个人）的预期结果、(ii)估计所有观察值接受治疗的概率、(iii)估计一个波动参数以告知更新初始结果估计的程度、(iv)更新初始结果估计、(v)计算平均治疗效果和标准误差（SE）用于统计推理。 3）因果森林：一种基于森林统计推理的治疗效果估计方法（105）。关于随机森林的详细解释，见表2。 4）双重机器学习（DML）：在二元处理的配置中，对于双重交叉拟合的情况，要进行以下步骤。(i) 该方法将数据随机分成两组；(ii) 对于第一组，使用ML在协变量的基础上预测结果；(iii) 对于第一组，使用ML在协变量的基础上预测治疗；(iv) 将(ii)得到的结果残差回归到治疗残差(iii)，得到一个模型。(v) 对于第二组，使用从(iv)中得到的模型来得到治疗效果的估计值；(vi) 对于第二组重复同样的程序；(vii) 对从两组得到的治疗估计值进行平均，进行最终估计(106)。

因果结构学习

1）基于约束的算法：首先学习一个无向图，然后确定方向，包括以下几种例子：(i) 稳定的PC算法（142）通过进行大量的条件独立性测试来学习DAG结构，并解决了经典PC算法（143）中的顺序依赖问题；(ii) 快速因果推理（144）是PC算法的扩展，当因果充分性的假设可能不被满足时，可说明可能的潜在变量。(iii) MMPC是一种两阶段的算法，用于学习网络中任何变量的直接原因和影响(145)；以及(iv) IAMB (146)使用Markov blanket的概念来减少条件独立性测试的数量（对于一个特定的变量，Markov blanket是最小的条件集，确保特定节点有条件地独立于图中的所有其他节点）。 2）基于分数的算法：在DAG上搜索，并根据指定的目标函数对每个DAG进行评分，包括以下几种例子：(i)   爬坡：从一个空图开始，迭代地进行局部的增加、删除或颠倒边缘，以提高图的得分（147）；(ii) Tabu搜索是爬坡的扩展，试图帮助算法摆脱局部模式（147）；(iii) 快速贪婪等价搜索：增加和删除多项式的边缘，在DAG的等价类空间中搜索（148）。 3）混合方法：结合基于约束的和基于分数的方法。例子：MMHC (149)使用基于约束的MMPC来建立DAG的骨架，然后使用基于分数的爬坡来确定方向。

6.1 应用1：反事实的推测

根据Hernán等人（6）的说法，“反事实预测是利用数据来预测世界的某些特征，就像世界已经不同一样”。如果寻求预测或反事实预测，判断答案是否有用得到一个标准是问目标是“解释还是预测？”(100)。尽管在某些情况下，可能能够估计因果效应的大小，但仍无法解释（例如，在一个试验中）(6)。潜在结果框架中的因果问题（用于反事实预测）可以用传统的方法来回答，如回归以及更先进的如边际结构模型（6）的方法。然而，在过去的几年里，用于因果推断的ML已经有了很大的发展，如果能够嵌入到因果推断和统计推断的框架中，将特别有帮助（101）。

6.1.1 常见的机器学习方法

对于反事实预测，ML可以用来分析大量的数据集。通过设置数据的方式来满足因果假设，然后使用预测性ML方法来回答因果问题（102）。如果数据设置得当，其他ML方法也很适合解决因果问题，如BART（103）、TMLE（104）和随机森林（105）。另一种回答因果问题的ML方法是双重机器学习（DML），它在高维数据中学习平均治疗效果和对被治疗者的平均治疗效果（106）。DML能够利用ML方法的准确预测，同时通过样本分割和交叉拟合提供无偏的、一致的估计，并提供有效的统计推断。强化学习也可以被概念化为一种方法，在有可能产生数据（A/B测试）的研究背景下接近因果推断。表3给出了使用潜在结果框架进行因果推断的常见ML方法的概述。

在某些情况下，已知变量的因果结构（部分），例如如果变量既相互联系又有时间顺序，或者遵循另一种因果逻辑（例如，研究者对自变量或另一个外在原因的操纵）。在数据科学领域，人们会提及结构化的高维输入。在这些情况下，可以使用ML中的图来纳入这种因果知识，并扩展LASSO或神经网络等预测算法，例如利用LASSO或卷积神经网络来反映因果结构。

BART的详细说明：本文介绍的BART是解决反事实预测的一种有趣的方法，因为它结合了典型的因果推断方法，例如倾向性评分加权来平衡治疗分配的概率与混杂因素来计算反事实，并用来估计治疗的效果，所以许多必要的研究者决定是明确的。更进一步，BART是树之和的模型，预测结果是单个回归树拟合的集合和一个加性高斯误差项的总和。每个回归树迭代地应用分割规则，将数据分割成不重叠的子集，目的是使每个子集的方差最小化（55, 103）。由于单个树过度强调相互作用，难以识别真正的线性关系，因此后续的树是根据识别子集的残差预测值来拟合的（103）。为了避免过度拟合，BART引入了树的大小（即子集/终端节点的数量）和收缩（即在子集中平整的因素）的正则化先验。然而，树的数量仍然是BART模型的一个调整参数（107）。对底层贝叶斯反拟合算法的更详细描述可以在其他地方找到(103)。BART的实施在回归和分类设置中都存在。与常见的基于树的ML方法（如随机森林或提升）不同，正则化优先权传达了灵活的趋势（如对小树），而不是由计算量大的网格搜索确定的固定参数。优先权进一步适用于高维数据和平滑回归函数（55）。实验结果表明，其性能可以与普通的方法相媲美或超过，如提升、神经网络、或随机森林。然而，特别是对于二元结果，交叉验证BART模型以选择正则化先验是有利的（55，103）。除了计算方面的好处外，BART 还适用于各种研究重点和结果（如生存和多叉逻辑回归），特别适合于因果推断任务，因为复杂反应面的建模和控制混杂不依赖于参数化的假设（55, 107）。由此产生的后验分布允许估计个人平均治疗或异质性因果效应。此外，基本的似然框架提供了关于结果的概率声明，包括可信区间，而识别和量化单个变量对结果的影响则更为复杂（107）。最近对BART的改编和实施进一步允许对治疗的概率进行建模并包括评分，以及在存在未观察到的混杂因素时模拟治疗效果。除此以外，还有一些程序缺少共识的程序可以控制(55)。

社会科学和健康科学中常见的因果推断的研究目的，通常用潜在的结果框架来解决，包括(i)评估不利的社会或健康结果的潜在原因、(ii)评估比较治疗效果、(iii)识别异质性治疗效果以及(iv)评估和可能消除统计分析中的偏见。

6.1.2 对社会和健康的潜在因素评估

为了评估潜在因素的效果，可以在控制混杂因素的情况下设计研究，以评估预测者对因果的影响。一项研究测试了准妈妈营养中的水果/蔬菜密度对不良妊娠和分娩结果的影响，结果显示，TMLE通过发现小的影响和给出更精确的估计，胜过了传统的建模（108）。在这个问题上更进一步，后续研究以双重稳健的ML显示，水果和蔬菜密度对子痫前期风险的保护作用被即将成为母亲的BMI所改变，保护作用随着BMI在20-30分之间的增加而加强，而对于BMI在30分以上的即将成为母亲的人来说，效果趋于平稳（109）。应用因果观点甚至有助于解决危重病人的肥胖悖论（110）。作为社会流动研究的一个例子，用回归树的纵向视角比较了父母和个人的社会经济收入决定因素(111)。

6.1.3 评估比较治疗的有效性

本节中研究人员可评估（例如干预与控制或照料）在改变健康结果方面最有效的几种治疗方法。关于卫生服务研究中更多临床应用的选择性概述见(112)。由于评估“治疗”在政策评估中也有相似之处，我们在(113)中回顾了经济学中基于ML估计平均治疗效应的发展。一项研究测试了认知行为疗法的目标处方，而以估计治疗结果为中心的人被分配到另一种治疗(=反事实结果) (114)。

6.1.4 识别异质性治疗效果

在随机处理分配的情况下，或者在评估新引入或改变的政策效果的时间研究设计中，反事实预测估计平均处理效应是直接的。此外，研究者可能希望识别和描述对治疗反应不同的亚组，即探讨异质性的治疗效果。异质性处理效应的分析可以回答公共卫生研究中尤为突出的问题：什么对谁最有效，什么时候最有效？技术详细说明请见估计处理效应异质性的文献(115)。随机森林已被开发用于检测异质性处理效应(105)。DML也被用来估计异质性处理效应(106)。

虽然临床试验的再分析是为了更好地理解对干预或药物治疗的反应中可能存在的异质性，但仍然需要谨慎：重新分析失败的试验的异质性治疗效应可以被认为是有问题的和P值操纵的形式，因为可用于再分析的试验通常被设计为产生平均效应( 116 )。总的来说，我们建议大多数使用ML识别异质性处理效应的方法用于假设生成，并在外部人群中验证特定的亚组效应。

6.1.5 评估和消除偏差

最后，一些有趣的ML应用已经被开发出来，以量化和解决针对因果推断的分析中的潜在偏差。在缺乏可忽略性（无不可测量的混杂因素）的情况下，对不可测量混杂的敏感性可能会严重限制研究结果的可推广性。“treatsens”程序包估计了一个不可测量的混杂因素的大小，这对于消除治疗与结果之间的联系是必要的；然而，这种分析需要领域知识(56)。在（或者实现不当）随机化有限的情况下，协变量的不平衡分布可能会使研究结果产生偏差。在这里，BART可以评估缺乏共同支持(117)，而协变量优先与匹配可以调整接受治疗的差异概率(118)。关于ML用于逆概率加权和倾向得分匹配的不同文献的综述见(102)。特别是在衰老研究方面，我们建议系统评估选择性磨蚀和竞争死亡风险带来的偏倚，如随机生存森林(119)已应用于痴呆研究(41)。

6.2 应用2：因果发现或因果结构学习

与Hernán等(6)的框架不同，其他方法认为因果推断不一定需要反事实预测(120)。虽然在卫生和社会科学中很少使用，但从数据中学习因果结构在可能产生（治疗手法）的情况下特别有趣。然而，即使在不可能进行治疗操纵的情况下，例如在有观察数据的情况下，因果结构学习也可以阐明因果研究问题：那么在（真实的或假设的）干预中随机分配暴露的意义上不能被操纵的推定原因呢? 我们认为，假想干预的缺失不应该限制我们估计因果效应，如性别，因为评估社会因素的效应大小是提高我们对所研究现象的理解和制定有针对性的干预措施的先决条件(121)。种族和性别/性别与社会经济和行为指标的不同关系能够深入了解社会状况(122)。种族或性别/性别等不可操作的变量可以通过允许操纵或某种形式干预的方式重新概念化，例如在维涅特研究中使用感知种族。然而，超越潜在结果框架，我们认为，在没有假设干预的情况下，我们可以利用结构因果学习，即使用能够从数据中学习（和呈现）变量的因果结构的算法。最近提出了队列数据中因果发现方法的指南(123)。在下文中，我们将首先对结构学习进行概述，然后转向从图形结构推导因果推理这一更为复杂的任务，即所谓的因果结构学习。

6.2.1 结构学习

我们首先考虑无向图的结构学习，即学习跨越复杂高维数据的条件独立结构。图形LASSO (124)在此设置中被广泛采用，并且基于一个潜在的高斯假设（即对于连续变量）。高斯图形LASSO的各种扩展已经被开发出来，包括同时学习和估计变量跨组（如对应不同的亚群或不同条件下收集的数据）和跨空间和/或时间（如纵向数据）的网络结构、混合变量（即对连续变量和离散变量的测量）和缺失数据的扩展。

这在数据稀疏的情况下尤其有趣，即包含许多空单元格，同时处理所有可用数据将付出极高的计算代价。最近的一项研究使用混合变量，即二元、连续和计数变量的潜在高斯图形模型来推断口头尸检中的症状关联(125)，这可能有助于得出更稳健的可能死亡原因分类。

6.2.2 因果结构学习

因果结构学习通过推断图中边的方向来扩展结构学习。基于约束的方法首先学习一个无向图，表示DAG的骨架，然后确定方向。或者，基于得分的方法直接在DAGs的空间上搜索，并根据指定的目标函数对每个图进行评分；随着节点/变量数量呈超指数增长的DAG数量庞大，需要精心设计搜索算法和评分。混合算法结合了基于约束和基于分数的方法的思想。Pearl (120)对因果关系进行了全面的技术概述，最近的因果结构学习综述在(126、127)中提供。噪声数据假设下因果结构学习算法的实证评估和比较见(128)。在因果结构学习的应用中，性能依赖于潜在假设（不同的模型依赖于不同的假设）的适当性，样本量对性能（从几百到两万不等）的影响很小，更稀疏的图更容易估计(127)。R中的BNLEARN包实现了多个基于约束和基于得分的因果结构学习算法(129)。基于约束的方法，特别是BNLEARN中的增量关联马尔科夫毯算法，已被用于识别撒哈拉以南非洲29个国家（130个）人口和健康调查中的HIV状态、检测和知识的风险因素（这可能是导致）。虽然数据是横截面的，没有不可测量的混杂，但缺乏HIV状况的社会行为决定因素，但存在HIV知识和检测的社会行为决定因素，这就使我们了解了在确定传染病传播时调查数据收集的局限性。另一项研究使用Markov和基于分数的快速贪婪等价搜索来识别种族和性别/性别等构成因素(122)。虽然性别主要与人格特征和行为有关，但种族与社会经济剥夺的系统性因素和行为有关，这与种族类别是在一个系统（结构性种族主义）(122)中构建的观点一致。

我们认为这些方法的应用需要经过这些方法培训的合作者对社会和健康研究人员进行培训，因为使用结构因果学习方法也意味着必须努力理解和交流调查结果。使用这种方法将产生更复杂的结果集，例如越来越多的可能竞争的图。随着对社会和健康科学中几乎所有学科的潜在结果框架的强烈强调，其他因果推断方法（及其潜在利益）在这个时候仍然是未知的。在讨论了用于描述、预测和因果推理的ML任务之后，我们将在下一节详细介绍最常见的ML性能指标。

7. 机器学习表现性能评估

在将ML方法映射到描述、预测和因果推理的研究目标之后，可以比较不同ML模型的性能或通过与更传统的统计方法相比评估ML。为了这个目的，表4给出了一个非详尽的常用的评估ML模型性能指标列表。通过评估模型的质量和性能，ML模型相比于传统的建模能够在社会和健康科学领域中提供间接的解决方案。例如，在经济学中需要满足常态性、一致性和效率的条件，并且可以进行相当的直接的测试（113）。

表4 综述与社会和健康科学中最相关的机器学习方法非技术描述

指标	解释和例子
无监督学习
聚类相关
ARI指数	度量两个数据聚类的相似性；与精度有关，但对于无标签数据。
互信息熵	度量相互依赖程度，评价两组变量的联合分布对各自边缘分布乘积的差异。
Calinski-Harabasz 指数	确定“正确”聚类数目的标准，几个相关的标准，例如，在kml包中实现对纵向数据的聚类
Dunn指数	验证聚类解
降维相关
重构误差	从推断的低维潜变量中测量观测数据和”重建数据”之间的距离(例如,连续数据的欧几里得)。
有监督学习
重要性指标	变量重要性量化了一个变量对分类或回归表现的个体贡献。有几种实现方式。对于基于树的模型，如随机森林，变量重要性通常被建模为使用变量在所有树上平均得到的改进之和( 4 )。在分类和回归中，通常5到10个最重要的变量可以被有意义地解释。
	由于重要性不容易与传统的统计学指标相比较，研究人员可以在多个模型中比较变量重要性，并考虑到统计学和临床(应用)重要性，增加一个随机变量作为基准。
回归相关
准确率	在所有预测( =真阳性+真阴性/真阳性+真阴性+假阳性+假阴性)上正确分类实例的比率。
	在(接近)平衡数据中的良好测量，即相似率的结果类。
	不要在不平衡数据中使用。
均衡准确率	灵敏度和特异度的算术平均值(见下文)；平均每个类别的正确分类案例的比例，在不平衡类中相关。
均方根误差	目标值与模型预测值之间的平均平方差。惩罚大的错误。
平方根误差	回归任务的首选度量。
	原始值与预测值之差的平方的平均值。
排列等级	评估跨模型或跨样本预测因子的重要性，如预测痴呆(41)。
风险比率	在回归中评估单个预测因子，如预测痴呆(41)，可以用置信区间报告。
绝对平均误差	原始值与预测值之间绝对差值的平均值。
分类相关
AUC	对于二分类结果的分类，该指标规定了ROC曲线下的面积，见下文，范围在0和1之间。数值越大，模型越好。
对数损失	度量一个分类模型的性能，该模型提供预测的类概率。当预测概率与实际类别值的偏差增大时，日志损失会变大。惩罚错误分类。在多类分类(见多项式对数损失)中效果良好。最小化日志损失会得到更高的准确率。
平均绝对百分比	预测精度的度量。它通常将准确率表示为一个比率。
精度	在二分类中，当误报代价较高时相关。
	正确分类病例占全部分类病例的比例(例如,被试)，百分比，=真阳性/ (真阳性+假阳性)。
正确率	适用于多类分类(具有两个以上类别)，易于解释。
召回率	在分类时，当漏报代价较高时，相关。
	所有实际阳性病例正确分类的比率[ (真阳性+假阴性)真阳性]。
	正确划分不同阶层的病例，如风险最高的阶层、风险中等的阶层、风险最低的阶层，如预测老兵自杀(71)。
ROC曲线	在二分类中。
	允许可视化真阳性率和假阳性率之间的权衡。ROC曲线显示了一个分类模型在所有分类阈值下的性能。
ROC面积	在二分类中。
	展示了在所有分类阈值下，真实阳性率(召回率/敏感度)与阳性预测值(精确度)之间的权衡。它与正例的低流行率的不平衡数据集相关，其中真正的正例需要被强调。
	数值越大，模型效果越好。
特异度	分类问题中。
	正确分类否定的比例，真实否定的比率。
	等于1个假阳性的比率。
F1指数	结合精确率和召回率，即F1值越高，误报率和漏报率越低。
因果相关
反事实预测
平均处理效应	如果所有观察都接受了治疗，与没有接受治疗的情况相比，结果的差异。
绝对偏差估计	对不可测量混杂的敏感性；treatsens中，未测量的混杂因素的估计值使得假定原因的影响为零[ ( 56 )中关于U的系数]。
比例中的点估计差异	比较两种处理的效果估计，例如BART和用于因果推断的其他算法；参见文献( 118 )例子；可以是平均或异质性处理效应。以95 %置信区间报告。
调整后风险差	候选原因的效果评价；TMLE中的关联平均处理效应；参见文献( 108 )例子。
	以95 %置信区间报告。
SE	给出了处理效应估计的置信度。通过计算进行统计推断，例如TMLE。
因果发现
SHD	通过将一个图转换为另一个图所需的变化的数量来比较两个图的度量，被广泛使用，但偏向于识别边的敏感性而不是特异性。
平衡计分函数	通过考虑混淆矩阵的所有元素来比较两个解决SHD中偏差的图的度量。
分类指标	可以使用特定于分类的指标如AUC或TPR (见上)来比较图，即真边率=真阳性率，假边数=假阳性，漏边率=假阴性。

 

虽然，生成的模型可以在ML框架内进行评估，即比较一系列模型并使用性能指标来选择模型。但相比于如逻辑回归的传统统计方法（如逻辑回归）的模型，基于ML的模型仍然是目前技术的最高水平。一些性能指标（如与分类有关的敏感性和特异性）适用于ML和非ML方法，并且可以跨框架使用。

8. 未来展望

通过使用描述、预测和因果推断等不同的研究目的，可以将社会和健康科学中的常见研究问题映射到适当的ML方法中。本文为这些研究目的提供了一个新的总结，将使ML在社会和健康科学中得到更系统的使用。虽然本文是迄今为止对ML在社会和健康科学中应用的最全面概述，但本文未包含使用ML的挑战，例如研究基础设施和计算要求，以及隐私和数据保护的问题。本文也只是略微触及了为更自动、更快速地处理大数据而开发的ML算法，例如语音或文本识别的自然语言处理和情感分析，并只提供了一些与全基因数据分析有关的例子。将SNA应用于旅游或营销在其他论文讨论过（53）。

如果通过深思熟虑地将其应用于相关问题，ML方法有可能极大地改善经验分析，最好是通过在社会或健康科学领域受过训练的研究人员与受过方法学训练的研究人员之间的合作。希望本文能够系统总结并推动最近在社会和健康研究中发展起来的ML方法。

参考文献

1. T. L. Wiemken, R. R. Kelley, Machine learning in epidemiology and health outcomes

research. Ann. Rev. Public Health 41, 21–36 (2020).

2. T. Yarkoni, J. Westfall, Choosing prediction over explanation in psychology: Lessons

from machine learning. Perspect. Psychol. Sci. 12, 1100–1122 (2017).

3. H. R. Varian, Big data: New tricks for econometrics. J. Econ. Perspect. 28, 3–28 (2014).

4. J. Friedman, T. Hastie, R. Tibshirani, The Elements of Statistical Learning (Springer Series in Statistics, Springer, 2001), vol. 1.

5. G. James, D. Witten, T. Hastie, R. Tibshirani, An Introduction to Statistical Learning

(Springer, 2013), vol. 112.

6. M. A. Hernán, J. Hsu, B. Healy, A second chance to get causal inference right:

A classification of data science tasks. Chance 32, 42–49 (2019).

7. J. Tukey, Exploratory Data Analysis (Addison-Wesley Series in Behavioral Science:

Quantitative Methods, Addison-Wesley, 1977).

8. I. Y. Chen, E. Pierson, S. Rose, S. Joshi, K. Ferryman, M. Ghassemi, Ethical machine learning in healthcare. Annu. Rev. Biomed. Data Sci. 4, 123–144 (2021).

9. W. J. Murdoch, C. Singh, K. Kumbier, R. Abbasi-Asl, B. Yu, Definitions, methods,

and applications in interpretable machine learning. Proc. Natl. Acad. Sci. U.S.A. 116,

22071–22080 (2019).

10. S. J. Pan, Q. Yang, A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 22,

1345–1359 (2009).

11. Y. Gao, Y. Cui, Deep transfer learning for reducing health care disparities arising

from biomedical data inequality. Nat. Commun. 11, 5131 (2020).

12. M. Kuhn, K. Johnson, Applied Predictive Modeling (Springer, 2013), vol. 26.

13. D. Donoho, J. Tanner, Observed universality of phase transitions in high-dimensional

geometry, with implications for modern data analysis and signal processing. Phil. Trans.

R. Soc. A 367, 4273–4293 (2009).

14. C. Ding, H. Peng, Minimum redundancy feature selection from microarray gene expression data. J. Bioinform. Comput. Biol. 3, 185–205 (2005).

15. F. Yu, C. Wei, P. Deng, T. Peng, X. Hu, Deep exploration of random forest model boosts the interpretability of machine learning studies of complicated immune responses and lung burden of nanoparticles. Sci. Adv. 7, eabf4130 (2021)

16. M. Anthony, P. Bartlett, Neural Network Learning: Theoretical Foundations (Cambridge Univ. Press, 1999).

17. M. A. Hernán, Does water kill? A call for less casual causal inferences. Ann. Epidemiol. 26, 674–680 (2016).

18. R. D. King, O. I. Orhobor, C. C. Taylor, Cross-validation is safe to use. Nat. Mach. Intell. 3, 276 (2021).

19. E. LeDell, S. Poirier, H2O AutoML: Scalable automatic machine learning. 7th ICML

Workshop on Automated Machine Learning (AutoML); www.automl.org/wp-content/

uploads/2020/07/AutoML_2020_paper_61.pdf.

20. F. Pedregosa, G. Vaorquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel,

P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, Scikit-learn: Machine learning

in Python. J. Mach. Learn. Res. 12, 2825–2830 (2011).

21. European Commission, Directorate General for Communications Networks, Content and Technology, High Level Expert Group on Artificial Intelligence, Ethics guidelines for

trustworthy AI (Publications Office, LU, 2019); https://data.europa.eu/doi/10.2759/177365.

22. C. Rudin, Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 1, 206–215 (2019).

23. K. J. Rohlfing, P. Cimiano, I. Scharlau, T. Matzner, H. M. Buhl, H. Buschmeier, E. Esposito, A. Grimminger, B. Hammer, R. Häb-Umbach, Explanation as a social practice: Toward a conceptual framework for the social design of AI systems. IEEE Trans. Cogn. Dev. Syst. 13, 717–728 (2020).

24. B. M. Greenwell, pdp: An R package for constructing partial dependence plots. R J. 9, 421–436 (2017).

25. S. M. Lundberg, G. G. Erion, S.-I. Lee, Consistent individualized feature attribution for tree ensembles. arXiv:1802.03888 [cs.LG] (12 February 2018).

26. S. Mangalathu, S.-H. Hwang, J.-S. Jeon, Failure mode and effects analysis of RC members based on machine-learning-based SHapley additive exPlanations (SHAP) approach. Eng. Struct. 219, 110927 (2020).

27. P. Hall, N. Gill, M. Kurka, W. Phan, Machine learning interpretability with h2o driverless ai (H2O.ai, 2017).

28. S. Barocas, M. Hardt, A. Narayanan, Fairness in Machine Learning (fairmlbook.org, 2019), vol. 1.

29. Z. Obermeyer, B. Powers, C. Vogeli, S. Mullainathan, Dissecting racial bias in an algorithm used to manage the health of populations. Science 366, 447–453 (2019).

30. S. Mitchell, E. Potash, S. Barocas, A. D’Amour, K. Lum, Algorithmic fairness: Choices,

assumptions, and definitions. Annu. Rev. Stat. Appl. 8, 141–163 (2021).

31. S. R. Pfohl, A. Foryciarz, N. H. Shah, An empirical characterization of fair machine learning for clinical risk prediction. J. Biomed. Inform. 113, 103621 (2021).

32. C. Birkenbihl, M. A. Emon, H. Vrooman, S. Westwood, S. Lovestone; AddNeuroMed

Consortium, M. Hofmann-Apitius, H. Fröhlich, Differences in cohort study data affect

external validation of artificial intelligence models for predictive diagnostics of

dementia-lessons for translation into clinical practice. EPMA J. 11, 367–376 (2020).

33. A. Tsymbal, The problem of concept drift: Definitions and related work. Computer Science Department, Trinity College Dublin. 106, 58 (2004).

34. M. Straat, F. Abadi, Z. Kan, C. Göpfert, B. Hammer, M. Biehl, Supervised learning in the presence of concept drift: A modelling framework. Neural Comput. Appl. 34, 101–118 (2022).

35. S. Salmi, S. Mérelle, R. Gilissen, W.-P. Brinkman, Content-based recommender support system for counselors in a suicide prevention chat helpline: Design and evaluation study. J. Med. Internet Res. 23, e21690 (2021).

36. L. Van Der Maaten, E. Postma, J. Van den Herik, Dimensionality reduction: A comparative. J. Mach. Learn. Res. 10, 66–71 (2009).

37. V. Kuan, H. C. Fraser, M. Hingorani, S. Denaxas, A. Gonzalez-Izquierdo, K. Direk, D. Nitsch, R. Mathur, C. A. Parisinos, R. T. Lumbers, Data-driven identification of ageing-related diseases from electronic health records. Sci. Rep. 11, 1–17 (2021).

38. S. M. Lundberg, B. Nair, M. S. Vavilala, M. Horibe, M. J. Eisses, T. Adams, D. E. Liston,

D. K.-W. Low, S.-F. Newman, J. Kim, Explainable machine-learning predictions for the

prevention of hypoxaemia during surgery. Nat. Biomed. Eng. 2, 749–760 (2018).

39. N. Demnitz, M. Anatürk, C. L. Allan, N. Filippini, L. Griffanti, C. E. Mackay, A. Mahmood, C. E. Sexton, S. Suri, A. G. Topiwala, E. Zsoldos, M. Kivimäki, A. Singh-Manoux, K. P. Ebmeier, Association of trajectories of depressive symptoms with vascular risk, cognitive function and adverse brain outcomes: The Whitehall II MRI sub-study.

J. Psychiatr. Res. 131, 85–93 (2020).

40. S. Amoretti, N. Verdolini, G. Mezquida, F. D. Rabelo-da-Ponte, M. J. Cuesta, L. Pina-Camacho, M. Gomez-Ramiro, C. De-la-Cámara, A. González-Pinto, C. M. Díaz-Caneja, I. Corripio, E. Vieta, E. de la Serna, A. Mané, B. Solé, A. F. Carvalho, M. Serra, M. Bernardo,

Identifying clinical clusters with distinct trajectories in first-episode psychosis through

an unsupervised machine learning technique. Eur. Neuropsychopharmacol. 47, 112–129

(2021).

41. J. Weiss, E. Puterman, A. A. Prather, E. B. Ware, D. H. Rehkopf, A data-driven prospective study of dementia among older adults in the United States. PLOS ONE 15, e0239994 (2020).

42. M. Hernán, J. Robins, Causal Inference: What If (Chapman & Hall/CRC, 2020).

43. A. Galozy, Towards understanding ICU procedures using similarities in patient

trajectories: An exploratory study on the MIMIC-III intensive care database (2018);

www.diva-portal.org/smash/get/diva2:1229433/FULLTEXT02.

44. W. Luo, T. Nguyen, M. Nichols, T. Tran, S. Rana, S. Gupta, D. Phung, S. Venkatesh,

S. Allender, Is demography destiny? Application of machine learning techniques

to accurately predict population health outcomes from a minimal demographic dataset.

PLOS ONE 10, e0125602 (2015).

45. H. Wang, A. Rodríguez, Identifying pediatric cancer clusters in florida using log-linear models and generalized lasso penalties. Stat. Public Policy 1, 86–96 (2014).

46. E. L. Aiken, A. T. Nguyen, C. Viboud, M. Santillana, Toward the use of neural networks

for influenza prediction at multiple spatial resolutions. Sci. Adv. 7, eabb1237 (2021).

47. J. C. Eichstaedt, R. J. Smith, R. M. Merchant, L. H. Ungar, P. Crutchley, D. Preoţiuc-Pietro, D. A. Asch, H. A. Schwartz, Facebook language predicts depression in medical records. Proc. Natl. Acad. Sci. U.S.A. 115, 11203–11208 (2018).

48. L. C. de Langavant, E. Bayen, A. Bachoud-Lévi, K. Yaffe, Approximating dementia

prevalence in population-based surveys of aging worldwide: An unsupervised machine

learning approach. Alzheimers Dementia 6, e12074 (2020).

49. S. I. R. Bhagyashree, K. Nagaraj, M. Prince, C. H. Fall, M. Krishna, Diagnosis of Dementia by Machine learning methods in epidemiological studies: A pilot exploratory study from south India. Soc. Psychiatry Psychiatr. Epidemiol. 53, 77–86 (2018).

50. K. Z. Gianattasio, A. Ciarleglio, M. C. Power, Development of algorithmic dementia

ascertainment for racial/ethnic disparities research in the US health and retirement study. Epidemiology 31, 126–133 (2020).

51. M. Morris, M. S. Handcock, D. R. Hunter, Specification of exponential-family random

graph models: Terms and computational aspects. J. Stat. Softw. 24, 1548–7660 (2008).

52. P. Barberá, J. T. Jost, J. Nagler, J. A. Tucker, R. Bonneau, Tweeting from left to right: Is

online political communication more than an echo chamber? Psychol. Sci. 26, 1531–1542 (2015).

53. D. Camacho, A. Panizo-LLedot, G. Bello-Orgaz, A. Gonzalez-Pardo, E. Cambria, The four dimensions of social network analysis: An overview of research methods, applications, and software tools. Inf. Fusion 63, 88–120 (2020).

54. J. Fan, R. Li, Variable selection via nonconcave penalized likelihood and its oracle

properties. J. Am. Stat. Assoc. 96, 1348–1360 (2001).

55. J. L. Hill, A. Linero, J. Murray, Bayesian additive regression trees: A review and look forward. Annu. Rev. Stat. Appl. 7, 251–278 (2020).

56. V. Dorie, M. Harada, N. B. Carnegie, J. L. Hill, A flexible, interpretable framework

for assessing sensitivity to unmeasured confounding. Stat. Med. 35, 3453–3470 (2016).

57. V. Svetnik, A. Liaw, C. Tong, J. C. Culberson, R. P. Sheridan, B. P. Feuston, Random forest: A classification and regression tool for compound classification and QSAR modeling. J. Chem. Inf. Comput. Sci. 43, 1947–1958 (2003).

58. B. Seligman, S. Tuljapurkar, D. Rehkopf, Machine learning approaches to the social

determinants of health in the health and retirement study. SSM Popul. Health 4, 95–99 (2018).

59. J. H. Friedman, Stochastic gradient boosting. Comput. Stat. Data Anal. 38, 367–378 (2002).

60. T. Hothorn, P. Bühlmann, T. Kneib, M. Schmid, B. Hofner, mboost: Model-based boosting (R package version, 2012).

61. A. I. Naimi, L. B. Balzer, Stacked generalization: An introduction to super learning.

Eur. J. Epidemiol. 33, 459–464 (2018).

62. H. S. Laqueur, A. B. Shev, R. M. C. Kagawa, SuperMICE: An ensemble machine learning approach to multiple imputation by chained equations. Am. J. Epidemiol. 191, 516–525 (2022).

63. T. Fine, M. Hassoun, Fundamentals of artificial neural networks [Book Reviews]. IEEE Trans. Inf. Theory 42, 1322–1324 (1996).

64. S. Dreiseitl, L. Ohno-Machado, Logistic regression and artificial neural network

classification models: A methodology review. J. Biomed. Inform. 35, 352–359 (2002).

65. F. Harrell, Regression Modeling Strategies. With Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis (Springer, 2015).

66. R. Neal, Bayesian Learning for Neural Networks (Springer, 2012).

67. C. Szegedy, W. Zaremba, I. Sutskever, J. Bruna, D. Erhan, I. Goodfellow, R. Fergus,

Intriguing properties of neural networks. arXiv:1312.6199 [cs.CV] (19 February 2014).

68. G. Carbone, M. Wicker, L. Laurenti, A. Patane, L. Bortolussi, G. Sanguinetti, Robustness of bayesian neural networks to gradient-based attacks. Adv. Neural Inf. Process. Syst. 33, 15602–15613 (2020).

69. I. Kavakiotis, O. Tsave, A. Salifoglou, N. Maglaveras, I. Vlahavas, I. Chouvarda, Machine learning and data mining methods in diabetes research. Comput. Struct. Biotechnol. J. 15, 104–116 (2017).

70. M. Beeksma, S. Verberne, A. van den Bosch, E. Das, I. Hendrickx, S. Groenewoud,

Predicting life expectancy with a long short-term memory recurrent neural network

using electronic medical records. BMC Med. Inform. Decis. Mak. 19, 36 (2019).

71. R. C. Kessler, I. Hwang, C. A. Hoffmire, J. F. McCarthy, M. V. Petukhova, A. J. Rosellini,

N. A. Sampson, A. L. Schneider, P. A. Bradley, I. R. Katz, C. Thompson, R. M. Bossarte,

Developing a practical suicide risk prediction model for targeting high-risk patients

in the Veterans Health Administration. Int. J. Methods Psychiatr. Res. 26, e1575 (2017).

72. S. Rose, Mortality risk score prediction in an elderly population using machine learning. Am. J. Epidemiol. 177, 443–452 (2013).

73. E. Christodoulou, J. Ma, G. S. Collins, E. W. Steyerberg, J. Y. Verbakel, B. Van Calster,

A systematic review shows no performance benefit of machine learning over logistic

regression for clinical prediction models. J. Clin. Epidemiol. 110, 12–22 (2019).

74. V. Baćak, E. H. Kennedy, Principled machine learning using the super learner:

An application to predicting prison violence. Sociol. Methods Res. 48, 698–721 (2019).

75. J. Blumenstock, G. Cadamuro, R. On, Predicting poverty and wealth from mobile phone metadata. Science 350, 1073–1076 (2015).

76. A. M. Alaa, T. Bolton, E. Di Angelantonio, J. H. Rudd, M. van der Schaar, Cardiovascular disease risk prediction using automated machine learning: A prospective study of 423,604 UK Biobank participants. PLOS ONE 14, e0213653 (2019).

77. S. Licher, M. J. Leening, P. Yilmaz, F. J. Wolters, J. Heeringa, P. J. Bindels; Alzheimer’s Disease Neuroimaging Initiative, M. W. Vernooij, B. C. Stephan, E. W. Steyerberg, M. Kamran Ikram, M. Arfan Ikram, Development and validation of a dementia risk prediction model in the general population: An analysis of three longitudinal studies. Am. J. Psychiatry 176, 543–551 (2019).

78. D. E. Goin, K. E. Rudolph, J. Ahern, Predictors of firearm violence in urban communities: A machine-learning approach. Health Place 51, 61–67 (2018).

79. N. V. Chawla, K. W. Bowyer, L. O. Hall, W. P. Kegelmeyer, SMOTE: Synthetic minority

over-sampling technique. J. Artif. Intell. Res. 16, 321–357 (2002).

80. H. Kvamme, N. Sellereite, K. Aas, S. Sjursen, Predicting mortgage default using

convolutional neural networks. Expert Syst. Appl. 102, 207–217 (2018).

81. M. Khalilia, S. Chakraborty, M. Popescu, Predicting disease risks from highly imbalanced data using random forest. BMC Med. Inform. Decis. Mak. 11, 51 (2011).

82. D. Facal, S. Valladares-Rodriguez, C. Lojo-Seoane, A. X. Pereiro, L. Anido-Rifon,

O. Juncos-Rabadán, Machine learning approaches to studying the role of cognitive

reserve in conversion from mild cognitive impairment to dementia. Int. J. Geriatr. Psychiatry 34, 941–949 (2019).

83. M. Grassi, D. A. Loewenstein, D. Caldirola, K. Schruers, R. Duara, G. Perna, A

clinically-translatable machine learning algorithm for the prediction of Alzheimer’s

disease conversion: Further evidence of its accuracy via a transfer learning approach.

Int. Psychogeriatr. 31, 937–945 (2019).

84. R. V. Marinescu, N. P. Oxtoby, A. L. Young, E. E. Bron, A. W. Toga, M. W. Weiner, F. Barkhof, N. C. Fox, A. Eshaghi, T. Toni, M. Salaterski, V. Lunina, M. Ansart, S. Durrleman, P. Lu, S. Iddi, D. Li, W. K. Thompson, M. C. Donohue, A. Nahon, Y. Levy, D. Halbersberg, M. Cohen, H. Liao, T. Li, K. Yu, H. Zhu, J. G. Tamez-Pena, A. Ismail, T. Wood, H. C. Bravo, M. Nguyen,N. Sun, J. Feng, B. T. Thomas Yeo, G. Chen, K. Qi, S. Chen, D. Qiu, I. Buciuman, A. Kelner, R. Pop, D. Rimocea, M. M. Ghazi, M. Nielsen, S. Ourselin, L. Sorensen, V. Venkatraghavan, K. Liu, C. Rabe, P. Manser, S. M. Hill, J. Howlett, Z. Huang, S. Kiddle, S. Mukherjee, A. Rouanet, B. Taschler, B. D. M. Tom, S. R. White, N. Faux, S. Sedai, Javier de Velasco Oriol, E. E. V. Clemente, K. Estrada, L. Aksman, A. Altmann, C. M. Stonnington, Y. Wang, J. Wu, V. Devadas, C. Fourrier, L. L. Raket, A. Sotiras, G. Erus, J. Doshi, C. Davatzikos, J. Vogel, A. Doyle, A. Tam, A. Diaz-Papkovich, E. Jammeh, I. Koval, P. Moore, T. J. Lyons, J. Gallacher, J. Tohka, R. Ciszek, B. Jedynak, K. Pandya, M. Bilgel, W. Engels, J. Cole, P. Golland, S. Klein, D. C. Alexander, The Alzheimer’s disease prediction of longitudinal evolution (TADPOLE) challenge: Results after 1 year follow-up. arXiv:2002.03419 [q-bio.PE] (9 February 2020).

85. K. Z. LeWinn, N. R. Bush, A. Batra, F. Tylavsky, D. Rehkopf, Identification of modifiable

social and behavioral factors associated with childhood cognitive performance.

JAMA Pediatr. 174, 1063–1072 (2020).

86. O. Weller, L. Sagers, C. Hanson, M. Barnes, Q. Snell, E. S. Tass, Predicting suicidal thoughts and behavior among adolescents using the risk and protective factor framework: A large-scale machine learning approach. PLOS ONE 16, e0258535 (2021).

87. N. Kimura, Y. Aso, K. Yabuuchi, M. Ishibashi, D. Hori, Y. Sasaki, A. Nakamichi, S. Uesugi, H. Fujioka, S. Iwao, M. Jikumaru, T. Katayama, K. Sumi, A. Eguchi, S. Nonaka, M. Kakumu, E. Matsubara, Modifiable lifestyle factors and cognitive function in older people: A cross-sectional observational study. Front. Neurol. 10, 401 (2019).

88. R. C. Schell, B. Allen, W. C. Goedel, B. D. Hallowell, R. Scagos, Y. Li, M. S. Krieger, D. B. Neill, B. D. Marshall, M. Cerda, J. Ahern, Identifying predictors of opioid overdose death at a neighborhood level with machine learning. Am. J. Epidemiol. 191, 526–533 (2022).

89. J. M. Platt, K. A. McLaughlin, A. R. Luedtke, J. Ahern, A. S. Kaufman, K. M. Keyes, Targeted estimation of the relationship between childhood adversity and fluid intelligence in a US population sample of adolescents. Am. J. Epidemiol. 187, 1456–1466 (2018).

90. J. C. Peterson, D. D. Bourgin, M. Agrawal, D. Reichman, T. L. Griffiths, Using large-scale experiments and machine learning to discover theories of human decision-making. Science 372, 1209–1214 (2021).

91. T. Ploner, S. Heß, M. Grum, P. Drewe-Boss, J. Walker, Using gradient boosting with stability selection on health insurance claims data to identify disease trajectories in chronic obstructive pulmonary disease. Stat. Methods Med. Res. 29, 3684–3694 (2020).

92. M. Anatürk, T. Kaufmann, J. H. Cole, S. Suri, L. Griffanti, E. Zsoldos, N. Filippini,

A. Singh-Manoux, M. Kivimäki, L. T. Westlye, K. P. Ebmeier, A.-M. G. de Lange, Prediction

of brain age and cognitive age: Quantifying brain and cognitive maintenance in aging.

Hum. Brain Mapp. 42, 1626–1640 (2020).

93. M. M. Glymour, Using causal diagrams to understand common problems in social

epidemiology, in Methods in Social Epidemiology, J. M. Oakes, J. S. Kaufman, Eds.

(Wiley, ed. 2, 2006) pp. 393–428.

94. E. C. Matthay, M. M. Glymour, A graphical catalog of threats to validity: Linking social science with epidemiology. Epidemiology 31, 376–384 (2020).

95. P. W. Tennant, W. J. Harrison, E. J. Murray, K. F. Arnold, L. Berrie, M. P. Fox, S. C. Gadd,

C. Keeble, L. R. Ranker, J. Textor, Use of directed acyclic graphs (DAGs) in applied

health research: Review and recommendations. medRxiv 2019.12.20.19015511 (2019).

96. J. M. Robins, M. Á. Hernán, B. Brumback, Marginal structural models and causal inference in epidemiology. Epidemiology 11, 550–560 (2000).

97. X. García-Albéniz, J. Hsu, M. A. Hernán, The value of explicitly emulating a target trial when using real world evidence: An application to colorectal cancer screening. Eur. J. Epidemiol. 32, 495–500 (2017).

98. M. A. Hernán, J. M. Robins, Using big data to emulate a target trial when a randomized trial is not available. Am. J. Epidemiol. 183, 758–764 (2016).

99. I. M. Aris, A. L. Sarvet, M. J. Stensrud, R. Neugebauer, L.-J. Li, M.-F. Hivert, E. Oken,

J. G. Young, Separating algorithms from questions and causal inference with unmeasured exposures: An application to birth cohort studies of early body mass index rebound. Am. J. Epidemiol. 190, 1414–1423 (2021).

100. G. Shmueli, To explain or to predict? Stat. Sci. 25, 289–310 (2010).

101. L. B. Balzer, M. L. Petersen, Machine learning in causal inference: How do I love thee? Let me count the ways. Am. J. Epidemiol. 190, 1483–1487 (2021).

102. T. Blakely, J. Lynch, K. Simons, R. Bentley, S. Rose, Reflection on modern methods: When worlds collide—Prediction, machine learning and causal inference. Int. J. Epidemiol. 49, 2058–2064 (2020).

103. H. A. Chipman, E. I. George, R. E. McCulloch, BART: Bayesian additive regression trees. Ann. Appl. Stat. 4, 266–298 (2010).

104. M. S. Schuler, S. Rose, Targeted maximum likelihood estimation for causal inference in observational studies. Am. J. Epidemiol. 185, 65–73 (2017).

105. S. Wager, S. Athey, Estimation and inference of heterogeneous treatment effects using random forests. J. Am. Stat. Assoc. 113, 1228–1242 (2018).

106. V. Chernozhukov, D. Chetverikov, M. Demirer, E. Duflo, C. Hansen, W. Newey, J. Robins, Double/debiased machine learning for treatment and structural parameters. Econom. J. 21, C1–C68 (2018).

107. N. B. Carnegie, J. Wu, Variable selection and parameter tuning for BART modeling in the fragile families challenge. Socius 5, 2378023119825886 (2019).

108. L. M. Bodnar, A. R. Cartus, S. I. Kirkpatrick, K. P. Himes, E. H. Kennedy, H. N. Simhan,

W. A. Grobman, J. Y. Duffy, R. M. Silver, S. Parry, A. I. Naimi, Machine learning as a strategy to account for dietary synergy: An illustration based on dietary intake and adverse pregnancy outcomes. Am. J. Clin. Nutr. 111, 1235–1243 (2020).

109. L. M. Bodnar, A. R. Cartus, E. H. Kennedy, S. I. Kirkpatrick, S. M. Parisi, K. P. Himes, C. B. Parker, W. A. Grobman, H. N. Simhan, R. M. Silver, D. A. Wing, S. Perry, A. I. Naimi, A doubly robust machine learning-based approach to evaluate body mass index as a modifier of the association between fruit and vegetable intake and preeclampsia. Am. J. Epidemiol. 191, 1396–1406 (2022).

110. A. Decruyenaere, J. Steen, K. Colpaert, D. D. Benoit, J. Decruyenaere, S. Vansteelandt, The obesity paradox in critically ill patients: A causal learning approach to a casual finding. Crit. Care 24, 485 (2020).

111. P. Brunori, G. Neidhöfer, The evolution of inequality of opportunity in Germany: A machine learning approach. Rev. Income Wealth 67, 900–927 (2021).

112. S. Rose, Intersections of machine learning and epidemiological methods for health

services research. Int. J. Epidemiol. 49, 1763–1770 (2020).

113. S. Athey, G. W. Imbens, Machine learning methods that economists should know about. Annu. Rev. Econom. 11, 685–725 (2019).

114. J. Delgadillo, P. Gonzalez, S. Duhne, Targeted prescription of cognitive–behavioral

therapy versus person-centered counseling for depression using a machine learning

approach. J. Consult. Clin. Psychol. 88, 14–24 (2020).

115. K. Imai, M. Ratkovic, Estimating treatment effect heterogeneity in randomized program evaluation. Ann. Appl. Stat. 7, 443–470 (2013).

116. U. Shalit, Can we learn individual-level treatment policies from clinical data? Biostatistics 21, 359–362 (2020).

117. J. L. Hill, Y.-S. Su, Assessing lack of common support in causal inference using Bayesian nonparametrics: Implications for evaluating the effect of breastfeeding on children’s cognitive outcomes. Ann. Appl. Stat. 7, 1386–1420 (2013).

118. L. Keele, D. S. Small, Comparing covariate prioritization via matching to machine

learning methods for causal inference using five empirical applications. Am. Stat. 75,

1–9 (2021).

119. H. Ishwaran, U. B. Kogalur, E. H. Blackstone, M. S. Lauer, Random survival forests. Ann. Appl. Stat. 2, 841–860 (2008).

120. J. Pearl, Causality (Cambridge Univ. Press, 2009).

121. M. M. Glymour, D. Spiegelman, Evaluating public health interventions: 5. Causal inference in public health research—Do sex, race, and biological factors cause health outcomes? Am. J. Public Health 107, 81–85 (2017).

122. R. Quintana, What race and gender stand for: Using Markov blankets to identify

constitutive and mediating relationships. J. Comput. Soc. Sci. 5, 751–779 (2021).

123. R. M. Andrews, R. Foraita, V. Didelez, J. Witte, A practical guide to causal discovery with cohort data. arXiv:2108.13395 [stat.AP] (30 August 2021).

124. J. Friedman, T. Hastie, R. Tibshirani, Sparse inverse covariance estimation with the

graphical lasso. Biostatistics 9, 432–441 (2008).

125. Z. R. Li, T. H. McComick, S. J. Clark, Using Bayesian latent Gaussian graphical models to infer symptom associations in verbal autopsies. Bayesian Anal. 15, 781–807 (2020).

126. M. Scanagatta, A. Salmerón, F. Stella, A survey on Bayesian network structure learning from data. Prog. Artif. Intell. 8, 425–439 (2019).

127. C. Heinze-Deml, M. H. Maathuis, N. Meinshausen, Causal structure learning. Annu. Rev. Stat Appl. 5, 371–391 (2018).

128. A. C. Constantinou, Y. Liu, K. Chobtham, Z. Guo, N. K. Kitson, Large-scale empirical validation of Bayesian network structure learning algorithms with noisy data. Int. J. Approx. Reason. 131, 151–188 (2021).

129. M. Scutari, J.-B. Denis, Bayesian Networks: With Examples in R (Chapman and Hall/CRC, ed. 2, 2021).

130. Z. Baranczuk, J. Estill, S. Blough, S. Meier, A. Merzouki, M. H. Maathuis, O. Keiser,

Socio-behavioural characteristics and HIV: Findings from a graphical modelling analysis

of 29 sub-Saharan African countries. J. Int. AIDS Soc. 22, e25437 (2019).

131. M. Ester, H. Kriegel, J. Sander, X. Xu, A density-based algorithm for discovering clusters in large spatial databases with noise, in Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (AAAI, 1996), vol. 240, p. 6.

132. E. Schubert, J. Sander, M. Ester, H. P. Kriegel, X. Xu, DBSCAN revisited, revisited: Why and how you should (still) use DBSCAN. ACM Trans. Database Syst. 42, 1–21 (2017).

133. M. Jordan, R. Jacobs, Hierarchical mixtures of experts and the EM algorithm. Neural Comput. 6, 181–214 (1994).

134. S. Masoudnia, R. Ebrahimpour, Mixture of experts: A literature survey. Artif. Intell. Rev. 42, 275–293 (2014).

135. M. E. Tipping, C. M. Bishop, Probabilistic principal component analysis. J. R. Stat. Soc. Series B 61, 611–622 (1999).

136. I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, Y. Bengio, Generative adversarial nets, in Advances in Neural Information Processing Systems, Z. Ghahramani, M. Welling, C. Cortes, N. Lawrence, K. Q. Weinberger, Eds. (Curran Associates Inc., 2014), vol. 27.

137. D. P. Kingma, M. Welling, Auto-encoding variational bayes. arXiv:1312.6114 [stat.ML] (1 May 2014).

138. V. A. Padilha, R. J. G. B. Campello, A systematic comparative evaluation of biclustering techniques. BMC Bioinform. 18, 55 (2017).

139. G. E. Moran, V. Ročková, E. I. George, Spike-and-slab Lasso biclustering. Ann. Appl. Stat. 15, 148–173 (2021).

140. C. Cortes, V. Vapnik, Support-vector networks. Mach. Learn. 20, 273–297 (1995).

141. C. S. Bojer, J. P. Meldgaard, Kaggle forecasting competitions: An overlooked learning opportunity. Int. J. Forecast. 37, 587–603 (2021).

142. D. Colombo, M. H. Maathuis, Order-independent constraint-based causal structure

learning. J. Mach. Learn. Res. 15, 3741–3782 (2014).

143. P. Spirtes, C. Glymour, An algorithm for fast recovery of sparse causal graphs. Soc. Sci. Comput. Rev. 9, 62–72 (1991).

144. D. Colombo, M. H. Maathuis, M. Kalisch, T. S. Richardson, Learning high-dimensional directed acyclic graphs with latent and selection variables. Ann. Stat. 40, 294–321 (2012).

145. I. Tsamardinos, C. F. Aliferis, A. Statnikov, Time and sample efficient discovery of Markov blankets and direct causal relations, in Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (Association for Computing Machinery, 2003), pp. 673–678.

146. I. Tsamardinos, C. F. Aliferis, A. Statnikov, Algorithms for large scale Markov blanket

discovery. FLAIRS Conf. 2, 376–380 (2003b).

147. M. Scutari, C. Vitolo, A. Tucker, Learning Bayesian networks from big data with greedy search: Computational complexity and efficient implementation. Stat. Comput. 29, 1095–1108 (2019).

148. J. I. Alonso-Barba, J. A. Gámez, J. M. Puerta, Scaling up the greedy equivalence search algorithm by constraining the search space of equivalence classes. Int. J. Approx. Reason. 54, 429–451 (2013).

149. I. Tsamardinos, L. E. Brown, C. F. Aliferis, The max-min hill-climbing Bayesian network structure learning algorithm. Mach. Learn. 65, 31–78 (2006).

（参考文献可上下滑动查看）

因果表征学习读书会启动

详情请见：

连接因果科学与深度学习的桥梁：因果表征学习读书会启动

推荐阅读

• Sci. Adv.速递：机器学习预测细菌代谢系统的演化
• Nat. Comput. Sci.：预测极端罕见事件的机器学习算法
• 无量纲学习：机器学习识别无量纲数与标度律
  
• 《张江·复杂科学前沿27讲》完整上线！
• 成为集智VIP，解锁全站课程／读书会
• 加入集智，一起复杂！
  

点击“阅读原文”，报名读书会