PRX 速递:遗忘导致吸引子网络的混沌

关键词:大脑记忆系统,混沌理论,吸引子网络,Hopfield 模型,动力学平均场理论


论文题目:Forgetting Leads to Chaos in Attractor Networks 论文来源:Physical Review X 论文链接:https://journals.aps.org/prx/abstract/10.1103/PhysRevX.13.011009
吸引子网络是大脑记忆系统的一个很有影响力的理论。这一理论最近受到了在记忆任务中神经元记录的强烈时间变异性的观察的挑战。近日发表于 Physical Review X 的这项工作研究了一个稀疏连接的吸引子网络,其中记忆是根据 Hebbian 突触可塑性规则学习。
在总结了连续的、稀疏连接的 Hopfield 模型的已知结果后,作者们研究了一个模型,其中,新的记忆被连续学习,而旧的记忆被遗忘,使用在线突触可塑性规则。结果表明,对于优化存储容量的遗忘时间尺度,网络记忆检索动力学的定性特征与年龄相关:最近的记忆作为不动点吸引子检索,而旧的记忆作为具有强烈异质性和时间波动特征的混沌吸引子检索。因此,在网络相空间中,不动点吸引子和混沌吸引子并存。该网络呈现了统计上可区分的记忆状态的连续统,其中混沌波动在临界年龄以上突然出现,然后逐渐增加,直到记忆消失。
作者们创建了一个动力学平均场理论来分析年龄相关的动力学,并将该理论与大型网络的模拟进行比较。他们计算了存储记忆数量最大化的最佳遗忘时间尺度。结果发现,记忆能被检索的最大年龄由不稳定点决定,在这个不稳定点,旧的记忆会不稳定,而神经网络会收敛到最近的记忆。数值模拟结果表明,动力学平均场理论需要高度的稀疏性才能准确预测网络容量。为了测试结果的稳健性和生物学合理性,作者们在在线学习场景中数值研究了具有学习规则和从体内数据推断的传递函数的网络的动力学。研究发现,在简单模型中分析的网络动力学的所有方面在这个模型中也成立。这些结果对噪声具有很强的鲁棒性。
最后,该理论为有老化备忘录的延迟响应任务提供了具体的预测。特别是,它预测了与旧记忆相关的检索状态有更高程度的时间波动,而且还预测了旧记忆的波动应该更快。总的来说,吸引子网络理论以忘记旧记忆为代价不断学习新信息,可以解释皮层中观察到的检索状态的多样性,特别是皮层活动的强烈时间波动。
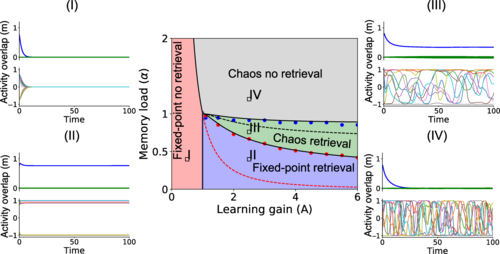

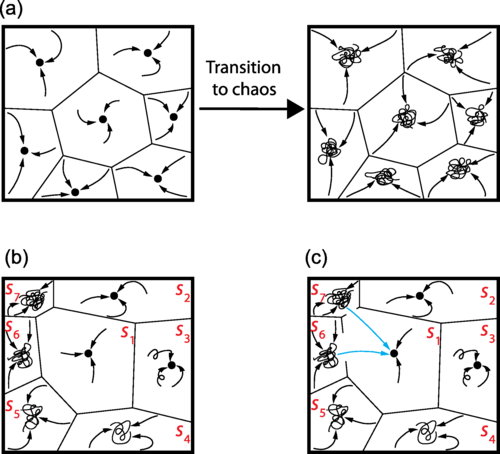
图3.吸引子网络相空间示意图。
神经动力学模型读书会

详情请见:
500+神经动力学社区成员,邀你共同点亮更多脑科学研究的岛屿
推荐阅读
-
Cell经典回顾:机器学习模型揭示大脑怎样整合空间记忆与关系记忆 -
Nat. Commun.速递:通过类睡眠回放克服神经网络的灾难性遗忘 -
常喝咖啡会改变大脑的结构和连接网络,有助于学习和记忆,但也带来更大压力 -
《张江·复杂科学前沿27讲》完整上线! -
成为集智VIP,解锁全站课程/读书会 -
加入集智,一起复杂!










