导语


“混沌边缘”（edge of chaos）是一种介于有序和无序（混沌）之间的动态机制，是复杂系统科学的核心概念。生命系统普遍存在某种“混沌边缘”？如果是，那么这会是自组织、进化以及复杂的自然和人工系统所须遵循的基本原则吗？这篇文章将回顾一些文献，主要关注“混沌边缘”的自然系统和人工系统中计算的基本原理。20世纪80年代，诺曼·帕卡德创造了“混沌边缘”这个词。从那时起，“适应混沌边缘”的概念在很多领域都得到了证明和研究，这些领域内的简单系统或复杂系统都会收到某种反馈。除了回顾古今的文献外，本文还将梳理对这一概念的批评声。


关键词：混沌边缘，混沌

Christof Teuscher | 作者

朱欣怡 | 译者

刘培源 | 审校

邓一雪 | 编辑



论文题目：
Revisiting the edge of chaos: Again?
论文地址：
https://www.sciencedirect.com/science/article/abs/pii/S0303264722000806


目录

1. 回到混沌边缘理论起点：从机械计算机到元胞自动机

2. 早期混沌边缘：元胞自动机与随机布尔网络

3. 批评的声音

4. 混沌边缘如何准确定义？

5. 生命系统处于临界状态吗？




1. 回到混沌边缘理论起点：

从机械计算机到元胞自动机



 
1665年，罗伯特·胡克（Robert Hooke）出版了《显微术》（Micrographia），首次对植物细胞作出了著名的描述。计算的历史也刚刚开始受到一些关注：帕斯卡（Pas元胞自动机l）在1642年设计了第一个可以执行加法和减法的机械计算器——帕斯卡林。后来，莱布尼茨（Leibnitz）改进了帕斯卡的发明，但直到19世纪20年代，Charles Babbage才设计出差分机，这是一种复杂得多的机械计算器，可以将多项式函数制成表格。之后又过了十多年，直到1936年图灵（Alan M. Turing）在他的著名论文里奠定了一些“现代计算”的关键基础，即概念图灵机（TM）和通用图灵机（UTM）（图灵，1936年至1937年）。在这个时间点，细胞生物学领域也取得了重大进展，不到一年，Hans Adolf Krebs才发现柠檬酸循环，也称为三羧酸循环或克雷布斯循环（Krebs和约翰逊，1937），这是一系列可以作为细胞主要能量来源的化学反应。

细胞生物学和计算的融合相当自然地创造了生物计算、分子计算和细胞计算领域。在图灵的开创性工作智能机械（图灵，1969）和形态发生（图灵，1952）中，他第一个介绍了上述概念。不久以后, Liberman在发展生物计算的范式和“细胞作为分子电脑”的概念的工作中成为先锋。关于这个主题，他最早的工作可以追溯到1972年，他介绍细胞是分子计算器,并可以使用分子语言控制自己（Liberman, 1972）。之后，在他1979年的论文（Liberman, 1979），Liberman描述了他所谓的分子细胞计算器 (MCC) ，并列出了更多的细节和它的基本特性。他还提出，“假定活细胞遵循现实或信息物理学”。在这篇文章最后，Michael Conrad评论道：“Liberman博士提出了一个不可避免的有争议的观点，即生命系统所需要的是一种信息物理学，它可能在某种程度上是从普通物理学修改而来的。”（Liberman，1979）。

Liberman 1972年的观点引发了关于物理学、生物学和信息论交叉的有趣问题，其中一些问题至今（部分或全部）仍未得到解答。物理学和生物学定律能从信息论中推导出来吗？物理学和生物学能发展新的方式处理信息吗？什么是生物信息？生物信息处理是否发生在某种“甜蜜点”或“混沌边缘”——一种介于有序与混沌之间的动态机制？如果是这样的话，这个“甜蜜点”是否是自组织、进化以及复杂的物理、生物和人工系统适应环境的基础？驱动系统达到某些“甜蜜点”的权衡原则是什么？

20多年后，Liberman已经找到了一些答案。例如，他在1996年与Minina合著的论文（Liberman and Minina，1996）中，提出了描述生物的四个统一原则：“建设‘新科学’似乎有益，它通过制定基本原则，以统一的观点描述生物和物质世界。我们认为这些原则是：1.用于计算和测量的最小代价原则；2.最优性原则；3.最小不可逆性原则；4.因果性原则（新措辞）。”

虽然Liberman从未使用过“混沌边缘”这个词，但他和Michael Conrad的开创性工作都暗示了一个最佳状态或“甜蜜点”，即生命系统中发生信息处理的地方，Conrad1989年的论文《脑-机反类比》（Conrad，1989）（后来由齐格勒（Zeigler，2002）重新审校）中可以清楚地反应这个观点，这本书里概述了进化性（或适应性）、效率和（结构）可编程性之间的权衡原则。物理限制导致了这样的权衡。“与当前机器熟悉的可编程领域完全不同，权衡原则意味着信息处理的高效率、高适应性领域。”（Conrad，1989）。

在这篇文章中，我们将回顾在自然系统和人工系统中“混沌边缘”的基本计算原理的文献。这个术语是Norman Packard在20世纪80年代末创造的（Packard，1988）。从那时起，“适应混沌边缘”的概念在许多领域得到了证明和研究，在这些领域中，简单系统和复杂系统都接收到某种反馈。除了回顾古今的文献外，我们还将回顾对这一概念的批评。请注意，本文不是关于混沌、自组织临界性和许多其他与非线性动力系统理论相关的子领域。我们将只触及这些主题的边缘，而主要是遵循“混沌的边缘”的故事线。




2. 早期混沌边缘：

元胞自动机与随机布尔网络



 
混沌边缘的早期研究主要集中在元胞自动机（元胞自动机）（Toffoli and Margolus，1987）和其他离散动力系统，如随机布尔网络（RBN）（Kauffman，1969）。在本节中，我们将重点介绍一些将混沌边缘研究引向不同的方向的早期工作。

1988年，在Norman Packard出版的书中，题为“适应混沌边缘”的章节中，“混沌边缘”一词诞生（Packard，1988年）。Packard提出了一个简单的自适应模型，该模型使用遗传算法（GA）来进化元胞自动机规则（Holland，1975）。他的模拟表明，“规则的群体总是朝着规则空间中的一个区域移动，这个区域标志着混沌规则和非混沌规则之间的边界”。这种行为可以解释为,首先, 观察得到在元胞自动机中需要通信以进行重要计算。Packard使用密度分类任务，该任务由元胞自动机自行决定初始状态中“1”的初始密度是否大于50%。如果大于50%，密度分类任务就要求元胞自动机朝着所有位置都是1的状态演化；如果密度小于50%，就要求元胞自动机朝着所有位置都是0的状态演化。单独看每一次实验都没有意义，因为每次都能计算出1的占比。然而，元胞自动机的细胞仅能看见附近的细胞（例如，半径为3），这使得该任务变得有价值，因为它要求细胞只进行局部通信而达到全局一致的状态。第二，可以直观地理解，根本不与邻居通信（或很少通信）的元胞自动机规则无法解决密度任务。帕卡德称这些规则是“无效的”。我们可以说这个系统太“死板”或太“有序”了，不能做任何有用的事情。另一方面，如果规定的交流太多，则任何局部扰动将很影响元胞自动机的状态，这也导致无法解决手头的任务。Packard称这些规则“非常活跃”，我们可以说它们属于规则空间中的“混沌”状态。他的结论是：“因此，可以合理地预计，任何需要这种通信的计算都只能通过接近混沌边缘的规则来完成”（Packard，1988）。

有趣的是， Wolfram在1984年发表过一篇很有影响力的论文（Wolfram，1984），其中他为一维元胞自动机引入了四个不同的普适类，并提出4类元胞自动机能够进行普适（或“复杂”）计算。但Packard并没有引用。虽然Wolfram和Langton在1986年发表的题为“用元胞自动机研究人工生命”（Langton，1986）的论文中，甚至都没有使用过“混沌边缘”这个术语，但他们还是为它的研究奠定了许多基础。例如，Langton提出了一个由虚拟状态机（VSM）组成的人工生物化学样本，作为一个“分子操作器”。他可能暗指混沌边缘，他指出“其中一个系统的例子，似乎很好地平衡了静止和混沌……为了动态地维持这种平衡，必须有某种有序的自我调节机制。” 但更值得注意的也许是Langton通过元胞自动机在模拟生物化学和人工分子之间建立的联系。“生物化学研究生命如何从无生命分子的相互作用中涌现……元胞自动机为我们提供了一个很好的人工宇宙，我们可以在其中嵌入虚拟自动机形式的人工分子” (Langton, 1986)。

几年后，Langton完全赶上了混沌边缘的潮流，发表了一篇现在仍被大量引用的文章（Langton，1990）。这篇文章展现出他的观点与Packard的观点相同：直觉上讲，接近混沌边缘的规则具有最好的信息通信能力，因此最适合计算。Langton再次使用了简单、统一和同步元胞自动机的框架：“本文介绍了元胞自动机的研究，它表明相变附近是支持实现信息传输、存储和修改的最佳条件。” 文章的最后，Langton指出：“系统在相变附近表现出一系列的行为，这些行为非常好地反映了计算现象学，我们认为，我们可以定位动力学行为谱中处于相变的计算定义为处于‘混沌边缘’”（Langton，1990）。Langton使用了参数𝜆（最初在Langton（1986）中引入），该参数用于从最同质到最异质规则表探索和表征元胞自动机规则空间的方法。然后他说明了参数𝜆也可以支持Wolfram的工作，并将Wolfram的元胞自动机四类和他自己的空间连接起来。

Langton在问题部分提出了提出了两点，与本文非常相关：

1. 他想知道他的工作与Bak的自组织临界性有何关系（Bak et al.，1988年）。

2. 他指出，相变现象在活细胞中随处可见。

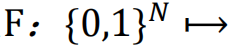
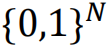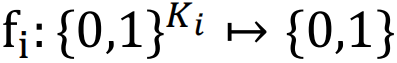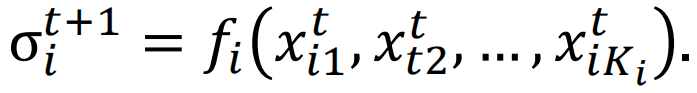
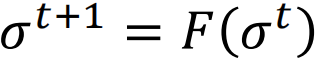第二，让我们回到Stuart Kauffman 1969年的论文（Kauffman，1969），在这篇论文中，他引入了正式遗传网络-也称为随机布尔网络（RBN），NK网络或NK模型，作为由二进制“开-关”基因组成的遗传调控网络的模型，用于研究细胞控制过程。在其最简单和原始的形式中，随机布尔网络是由𝑁个自动机（或节点）组成的离散动力系统，其中每个节点从其他随机选择的K个节点接收输入。结果是，每个节点平均具有𝐾个到其它节点的输出。每个节点都是布尔变量，只有两种可能的状态：{0，1}。而动力学满足，其中F=（f1，…，fi，…，fN），并且每个fi都由从𝑁个节点集合中随机选择的输入Ki的查找表来表示。最初，Ki个邻居和查找表被随机分配给每个节点：。每个节点的状态用相应的布尔函数更新：


每个节点用其相应的布尔函数同步更新：。经典的同步RBN的状态数目有限，并且在一定数目的时间步之后，𝑇将落入固定或循环吸引子。

Kauffman研究了三大类遗传网络的周期和扰动：（1）全连通𝐾 =𝑁，（2）𝐾= 1，（3）𝐾= 2。他得出结论，全连通网络（K=N）在生物学上是不可能的，𝐾=1级网络需要地球上任何生物都不具备的循环，𝐾=2级网络在生物学上是合理的。Kauffman认为，生物体中基因网络的参数是通过进化调整的，因此它们将在接近混沌边缘的关键阶段运行。更广泛地说，他的研究结果表明，混沌边缘的生物网络表现出稳定性、可进化性和信息处理效率，这与Conrad提出的权衡原则一致（Conrad，1989）。Derrida 和 Pomeau花了将近20年的时间，以及随后的在那个世纪末的许多其他人，才开始从更数学化的角度分析径向基神经网络（Derrida and Pomeau，1986）。

Kauffman在文章的结尾作了如下陈述：“由大的、随机组合的二进制元素组成的网络具有简单、稳定和有序的特性。大自然利用了这种可能的和可靠的系统，来创造进化和保护其后代”（Kaufman, 1969）。

让我们回顾一下：早期关于混沌边缘的工作主要集中在离散动力系统上，并提供了证据证明：在这种动力系统中复杂的动力学出现在某些相变附近， “依赖于处理信息的基本能力”（Langton，1990）。

故事继续之前，我们先来听一听批评的声音。




3. 批评的声音



 
Mitchell等人的文章总是被引作对混沌边缘的批评（Mitchell et al., 1993）。然而，事实并非如此。这些文章更像是对Packard的发现（Packard，1988）的具体批评，这些发现涉及统一的、一维的、同步的元胞自动机的进化、动力学和计算能力。Mitchell等人试图通过进行一组类似的实验来复现Packard的结果。不幸的是，Packard的论文遗漏了相当多的技术细节，这迫使Mitchell等人对几个参数做出了“合理”的假设。但遗憾的是，Mitchell等人根本无法重现Packard的结果：“我们的实验产生了完全不同的结果，我们认为对原始结果的解释是不正确的”（Mitchell et al., 1993）。虽然他们观察到更复杂的规则在演变，但这些规则似乎并不存在于混沌边缘。他们进一步指出“……我们不知道是什么原因造成我们的结果与原始实验结果之间的差异。”

Mitchell等人在他们的一般性讨论中明确指出，“我们给出的结果并没有反驳这个假设：计算能力与元胞自动机规则空间中的相变相关”。这一假设后来得到了一些作者的证实。

1995年，Gutowitz和Langton重新检查了是否存在混沌的边缘，以及演化是否能够引导系统到达混沌边缘（Gutowitz and Langton，1995）。他们认为，需要一种新的复杂性衡量标准来确定这些问题，并认为趋同时间是一个适当的指标。通过使用平均场方法，他们证明了：随着演化，元胞自动机规则确实变得越来越复杂，而且关键规则的平均收敛速度比非关键规则要慢。Kaneko和Suzuki（1994）以及Suzuki和Kaneko（1994）使用逻辑斯蒂图确定了混沌边缘，得出了类似的结果。他们还发现，在适当的条件下，演化过程确实会驱使一个系统走向混沌边缘。

1997年，Siper在他的书中报告说，他获得了支持Mitchell等人的结果（Siper，1997）。他使用自己的“元胞编程算法”进行实验，该算法依赖于局部适应性测量（与进化算法中的全局测量相反）。Siper发现的规则集中在𝜆= 0.5附近，大部分在0.45-0.55之间，这与Mitchell等人的研究结果一致。密度𝜆任务的值可能接近0.5。在他的实验中，更复杂的规则再次演化出来，但对于Packard有关混沌边缘的结果，人们存在分歧。

在结束本节时，我们再次强调Mitchell等人的文章是对Packard实验的批评，也是一次失败的尝试。他们的论点和发现完全依赖于统一的元胞自动机，而统一元胞自动机的规则是通过使用遗传算法进化而来的。这篇文章没有质疑混沌边缘的广泛存在，也没有质疑演化，或其他适应性反馈机制，可以推动系统走向混沌边缘。因此，引用这篇文章作为对混沌边缘的批评，就像它经常做的那样——是误导。例如，维基百科关于混沌边缘的文章确实指出，“然而，Melanie Mitchell和其他人对这一想法的普遍性和重要性提出了质疑”（Wikipedia，2022）。这是一个不准确的陈述，并且不反映Mitchell等人的结论。

事实上，在随后的一篇论文中，Mitchell等人（Mitchell et al.，1994）包含了一些额外的论点和观点，再次强调了“……我们的研究并不排除将来，在元胞自动机的背景下，有人能对“混沌边缘”一词作出严格而有用的定义。它们也不排除发现混沌边缘与元胞自动机的计算能力增强有关。最后，它们不排除自适应系统演化到这样的动态区域，以便利用那里固有的计算能力。”再早些时候，Crutchfield和Young就提供了大量证据（Crutchfield and Young ，1990）。




4. 混沌边缘如何准确定义？



 
到目前为止，我们还没有正式定义混沌边缘。现在让我们来谈谈这个问题。我们将探讨两种主要的方法来界定一般所认为的混沌边缘：（1）Derrida的模拟退火和（2）Lyapunov指数。

测量（通常很小的）局部扰动（又称“损伤”或噪声）在动力系统中的传播是一种确定系统处于何种状态的既定方式。为此，创建系统的两个副本，并在其中一个系统中引入一些扰动。然后随时间比较两个状态轨迹之间的距离：（1）当系统处于（确定性）混沌状态时，扰动会扩散；（2）如果系统处于有序（或“冻结”）区，扰动将消失；以及（3）如果系统处于混沌边缘的临界/复杂状态，则扰动将保持在恒定大小。因此，确定混沌边缘的主要问题是：扰动是消失、维持还是增长？或者换句话说，动力系统对初始条件的敏感度是多少？在临界阶段，即混沌边缘，扰动将在长时间和空间尺度上传播，既不衰减也不放大。

Kauffman在他1969年的论文中研究了扰动，并使用它们对随机布尔网络进行分类（Kauffman，1969）。1986年，Derrida和Pomeau提出了模拟退火法（AA），这是一种平均场方法（Derrida and Pomeau，1986），后来又有人进行了扩展，例如：(Solé and Luque, 1995, Luque and Solé, 1997)。Derrida和Pomeau的分析表明，在热力学极限下，即：当网络规模趋于无穷大时，可以精确确定临界点。对于Kauffman的随机网络，发现它们在稀疏临界连通度时表现出动态有序-无序转变。然而，在实际问题的应用中，热力学极限通常不是很重要。近期的工作更关注有限大小缩放，这既用于随机布尔网络（RBN），也用于随机阈值网络（RTN），可参见 (Rohlf and Bornholdt, 2002, Rämö et al., 2006, Samuelsson and Socolar, 2006, Lu and Teuscher, 2014, Ishii et al., 2019, Rohlf et al., 2007, Goudarzi et al., 2012) 。我们稍后将看到如何通过自组织实现随机布尔网络的关键连接。

李雅普诺夫指数𝜆测量动力系统（在相空间中的）两个轨迹之间的分离速率。因此，该指数能够测量不稳定程度，并确定混沌边缘。李雅普诺夫指数描述系统的短期行为，而最大李雅普诺夫指数（MLE）则描述系统的长期动态。一个正的（最大）李雅普诺夫指数表明系统对初始条件敏感，因此处于混沌状态。另一方面，如果𝜆＜0，则系统是稳定的或有序的。如果一个动力系统的最大李雅普诺夫指数为0，那么它会被认为处于混沌的临界状态的。

李雅普诺夫指数也可以从诸如CAs和RBNs等离散系统中被导出，可参见 (Bagnoli et al., 1992, Luque and Solé, 2000)。值得指出的是，混沌理论的许多工作都是基于连续和无限空间的假设，我们在这里就不讨论了。

最后但也很重要的是，定义复杂性是什么又不是什么，这仍然是一个开放的，或者说至少是一个有争议的问题。Solé等人指出：“已经提出了几种（复杂性的）定义，它们都共有一个直观概念，即复杂性既不是完全有序的，也不是完全无序的” (Solé et al., 1996)。




5. 生命系统处于临界状态吗？



 
如上文所提到的， Kauffman是第一个宣称并证明：生命系统，特别是基因调控网络，是在有序与混沌之间的临界动力学机制中运行的（Kauffman，1969）。Kauffman的假设之一是，细胞类型对应于Kauffman 随机布尔网络中的状态循环吸引子。Kauffman比Packard更进一步，Packard认为他的元胞自动机规则是自然选择的结果。Kauffman的研究结果是：遗传调控网络的性质是内在动态过程的结果。

从那时起，有充分的证据表明：准静态非平衡态生命物质在接近或等于混沌边缘的某种临界状态下运行，而临界状态是在不断平衡之后出现的。直观上，这很有道理，因为生命和非生命系统在对环境作出反应时都表现出不同的相变 (Griffiths and Wheeler, 1970, Jacobs and Frenkel, 2017) 。

后文，我们将提到一些特定的刊物，以强调生命系统临界性的概念。

在Packard的混沌边缘论文发表后不久，Ito和Gunji提出了更多的证据，证明自组织作为一种进化过程，推动着生命系统走向混沌边缘。他们还假设他们的自组织临界性是Bak的自组织临界性的一种推广形式（Ito and Gunji, 1994）。

2005年，Shmulevich等人 (2005) 首次证明了“……HeLa细胞的基本遗传网络似乎在有序状态下或在有序与混沌的边界上运行，但似乎不是混沌的。”Kesseli和Yli-Harja提出了一种研究基因调控网络关键性的新方法：“该方法是第一次使用生物学测量数据，来量化细胞是否动态有序、临界或混沌的尝试之一” (Rämö et al., 2006)。Nykter et al. (2008) 使用了巨噬细胞的基因表达数据，发现其动力学至关重要。Hanel 等人 (2010) 表明，他们用作生物反应网络模型的极最小非线性（MNL）系统也是如此。

Torres-Sosa 等人 (2012) 讨论了：基因网络如何真正达到临界行为？这仍然是一个有点难以捉摸的开放性问题。他们提出了“……一种进化模型，其中临界性自然地从可进化性的两个基本组成之间的平衡涌现而出：突变下的表型保守和表型创新”“……我们的结果表明，扩展新表型（创新）与保留现有表型（保留）之间的这种相互作用，足以导致种群中所有网络向临界状态进化。”

虽然Mora和Bialek没有提到混沌边缘，但他们的文章有问道：“生命系统是否处于临界状态？” (Mora and Bialek, 2011)。他们讨论了，在广泛的生命系统中临界性的实验证据，包括蛋白质网络、神经网络和鸟群。“诱人的可能性是，许多系统并不深处于一个相或另一个相，而是在自然参数空间的临界表面附近保持平衡。”

今天，仍然有一个半开放的问题：生命系统究竟是如何达到临界状态的？因为临界状态往往是整个参数空间中的一个很小的区域（如果不是一个点的话）。大多数证据表明，这是一个反馈机制和平衡演化的组合 (Ulanowicz, 2002, Conrad, 1989) 。




6. 混沌边缘研究的全盛时期



 
Kauffman在60年代末开始了随机布尔网络的研究（Kauffman，1969），而理论分析的全盛时期直到新世纪初才开始。随机布尔网络足够简单可以形式化和分析，但又足够复杂饶有趣味，对许多研究人员来说是一个完美的游乐场。统计物理学的现代工具与新出现的无穷无尽的计算资源相结合，使该领域蓬勃发展了许多年。

物理学家一致都对小型系统感兴趣，如logistic映射,或自组织演化到混沌边缘 (Pierre and Hübler, 1994, Baym and Hübler, 2006, Melby et al., 2000)。此外，多年来，随机布尔网络也派生出许多新属性。例如，在Kc处，吸引子周期的相空间结构（Albert and Barabási, 2000），不同吸引子的数量（Samuelsson and Troein, 2003），混沌吸引子的分布是复杂的（Bastolla and Parisi, 1998），显示出许多生物网络的属性 (Kaukman,1993) 。

2000年，Bornholdt 和 Rohlf (2000) 证明了一个简单的局部重连规则（静节点增长连边，动节点失去连边）可以驱动随机阈值网络（RTNs）——随机布尔网络的子集，在大型系统的极限下，达到临界平均连通性Kc=2。该结果后来被推广到随机布尔网络（Rohlf et al., 2007）。这个结论首次证明了：一个简单的自组织网络的局部规则可以导致它们进入临界状态。Liu 和 Bassler (2006) 使用了相同的重连规则，但在共同进化的过程中。他们发现“在演化过程中，临界态的涌现源于拓扑学和动力学的相互作用。”

Goudarzi 等人 (2012) 更进一步，解决了一个长期悬而未决的问题：他们通过计算发现，对于大规模（N）的系统，自适应信息处理驱使随机布尔网络的临界连通性Kc=2。对于有限规模的网络，连通度接近临界值，且与系统规模呈幂律关系𝑁。此外，他们还表明，如果任务复杂性和所提供的信息量超过了一定的复杂性阈值，网络学习和泛化在接近临界状态时会得到优化。

大约是2001年，出现了一种新的研究方向——库计算Reservoir Computing (RC)（Jaeger, 2001; Bertschinger and Natschläger, 2004, Maass et al., 2002, Legenstein and Maass, 2007）。库计算的主要思想是：1）一个递归神经网络作为一个固定的、典型地非线性的“储存器，”它将输入投影到一个更高维的空间；2）训练线性输出层将高维空间映射到期望的输出上，后一部分大大降低了训练的计算成本。库计算已经从一个边缘概念发展成为一个相当主流的计算框架（Büsing et al., 2010, Goudarzi and Teuscher, 2016）。库计算在时间信号处理领域尤其出色，然而，触须层可能是非结构化、不完美和不可靠的，这一事实引起了硬件界的关注，因为它有可能使储层的构建比传统硬件更容易、更便宜。这又引出了另一个新领域：非物质计算（Lilak et al., 2021, Dale et al., 2017, Hochstetter et al., 2021）。神经形态计算社区对这一领域特别感兴趣，因为它直接利用物理学来实现神经网络的潜力，而不是建立传统的冯·诺依曼体系结构然后“模拟”神经网络（Nakajima et al., 2021, Hochstetter et al., 2021, Cao et al., 2022, Tran and Teuscher, 2021, Slavova and Ignatov, 2022）。

库计算成为研究者研究混沌边缘的最新游乐场之一。Boedecker等人（2012年）使用了一个信息理论框架，表明当储蓄层处于稳定和不稳定状态之间时，即混沌边缘，回声状态网络（库计算的一种变体）的计算能力最大。Snyder等人（2013年）指出，随机布尔网络库计算中的本征计算能力，在系统处于混沌边缘时达到最大。Carroll （2020）最近的研究似乎与早期处于混沌边缘的库计算相关的许多研究相矛盾：“动力系统的最佳计算能力出现在稳定性边缘，这一概念，通常是不正确的。本文展示了最佳性能不在稳定性边缘的库计算。” Carroll将混沌边缘（EoC）重新定义为稳定性边缘（EoS），即最大Lyapunov指数变为正值的点。值得注意的是，他的结果只基于单一任务和单一储层大小。这个结果是否适用于更普遍的情况还有待观察。




7. 结论与展望



 
在许多科学领域内，研究结构与随机、有序与混沌之间的平衡都很常见。当然，计算领域也不例外。在混沌边缘计算的概念吸引了相当多的关注，因为它的起源相当抽象——源于算法。多年来，混沌边缘的概念也早已在信息处理之外得到了应用，例如Dambisa Moyo关于社会经济问题的书（Moyo，2018），Oswald等人在处于混沌边缘的关于项目管理的书（Oswald et al., 2018），以及Pamela McCorduck的小说（McCorduck，2007）也对此进行了说明。

混沌边缘是否遵循Gartner的技术炒作周期（Blosch and Fenn, 2018）？该周期包括五个阶段：（1）技术触发，（2）膨胀预期的顶峰，（3）幻灭的低谷，（4）启蒙的斜坡，（5）生产力的平台期。我们认为答案是否定的。虽然最初可能有一些膨胀的期望达峰，但混沌边缘似乎并未经历过幻灭的低谷。相反，在80年代末的技术触发后，多年来逐步达到了生产力的平台期。Mitchell等人的论文（Mitchell et al., 1993）可能在混沌边缘发展的道路上造成了微小的颠簸，但似乎并没有改变研究的总体进程。

许多复杂系统，尤其是活细胞，在维持其时空组织方面表现出非凡的稳定性，但同时，它们也能够适应环境中的各种变化。一个生命的求生本能要求它能整合和处理有限的资源，并对环境的变化作出反应。因此，系统必须处理如有限的能量、资源、空间、时间等的反馈和平衡，才能活下去。它们大致符合Liberman 和 Minina (1996) 提出的四个统一的生物基本原则。也有人假设，生命系统进化进程中被自然选择的依据是在混沌边缘附近执行复杂信息处理的能力。有人提出并研究了几种机制，它们将生命系统以及抽象的非生命系统（如RBN）驱动到临界状态。这样的自组织有多少是目标导向的，有多少不是？仍是一个悬而未决的问题。

Liberman开创和发展的一个概念：细胞是分子计算机——通常被视为生命系统如何组织和运行的模型（Liberman，1972）。这种观点下，计算机被视作处于临界状态的物理系统。它们要在一定的宏观“计算”自由度内支持任意长的时间相关性。这通过将这些自由度与产生误差的热浴自由度解耦来实现。计算机是一种物理系统，在熵无序环境中处于连续相变状态。在这样的环境里，计算机获得了推动计算向前发展的驱动力。但同时，它们必须保护计算不受环境引起的波动的影响（Crutchfield and Young, 1990）。

总结如下：根据Betteridge定律和Hinchcliffe规则（Cook and Plourde，2016），当文章标题提出是或否的问题时，问题的答案通常是否定的。目前似乎也没有必要重寻混沌边缘。我们可以很有信心地说，这一概念已经确立，且在各个领域，以各种方法得到了证明。


参考文献

Albert, R., Barabási, A.L., 2000. Dynamics of complex systems: Scaling laws for the
period of boolean networks. Phys. Rev. Lett. 84 (5660).
Bagnoli, F., Rechtman, R., Ruffo, S., 1992. Damage spreading and Lyapunov exponents
in cellular automata. Phys. Lett. A 172, 34–38. http://dx.doi.org/10.1016/0375-
9601(92)90185-O.
Bak, P., Tang, C., Wiesenfeld, K., 1988. Self-organized criticality. Phys. Rev. A 38,
364–374. http://dx.doi.org/10.1103/PhysRevA.38.364.
Bastolla, U., Parisi, G., 1998. The modular structure of Kauffman networks. Physica D
115, 219–233.
Baym, M., Hübler, A.W., 2006. Conserved quantities and adaptation to the edge of
chaos. Phys. Rev. E 73, 056210. http://dx.doi.org/10.1103/PhysRevE.73.056210.
Bertschinger, N., Natschläger, T., 2004. Real-time computation at the edge of chaos in
recurrent neural networks. Neural Comput. 16, 1413–1436. http://dx.doi.org/10.
1162/089976604323057443.
Blosch, M., Fenn, J., 2018. Understanding Gartner’s hype cycles. https://www.gartner.
com/en/documents/3887767.
Boedecker, J., Obst, O., Lizier, J.T., Mayer, N.M., Asada, M., 2012. Information
processing in echo state networks at the edge of chaos. Theory Biosci. 131,
205–213.
Bornholdt, S., Rohlf, T., 2000. Topological evolution of dynamical networks: Global
criticality from local dynamics. Phys. Rev. Lett. 84, 6114–6117.
Büsing, L., Schrauwen, B., Legenstein, R., 2010. Connectivity, dynamics, and memory
in reservoir computing with binary and analog neurons. Neural Comput. 22,
1272–1311. http://dx.doi.org/10.1162/neco.2009.01-09-947.
Cao, J., Zhang, X., Cheng, H., Qiu, J., Liu, X., Wang, M., Liu, Q., 2022. Emerg-
ing dynamic memristors for neuromorphic reservoir computing. Nanoscale 14,
289–298.
Carroll, T.L., 2020. Do reservoir computers work best at the edge of chaos? Chaos: An
interdisciplinary. J. Nonlinear Sci. 30, 121109.
Conrad, M., 1989. The brain-machine disanalogy. BioSystems 22, 197–213.
Cook, J.M., Plourde, D., 2016. Do scholars follow betteridge’s law? The use of questions
in journal article titles. Scientometrics 108, 1119–1128. http://dx.doi.org/10.1007/
s11192-016-2030-2.
Crutchfield, J.P., Young, K., 1990. Computation at the onset of chaos. In: Zurek, W.H.
(Ed.), Complexity, Entropy, and the Physics of Information. Addison-Wesley,
Redwood City, CA, pp. 223–269.
Dale, M., Stepney, S., Miller, J.F., Trefzer, M., 2017. Reservoir computing in materio:
A computational framework for in materio computing. In: 2017 International
Joint Conference on Neural Networks. IJCNN, pp. 2178–2185. http://dx.doi.org/
10.1109/IJCNN.2017.7966119.
Derrida, B., Pomeau, Y., 1986. Random networks of automata: A simple annealed
approximation. Europhys. Lett. 1, 45–49.
Goudarzi, A., Teuscher, C., 2016. Reservoir computing: Quo vadis? In: Proceed-
ings of the 3rd ACM International Conference on Nanoscale Computing and
Communication. 13, pp. 13:1–13:6. http://dx.doi.org/10.1145/2967446.2967448.
Goudarzi, A., Teuscher, C., Gulbahce, N., Rohlf, T., 2012. Emergent criticality through
adaptive information processing in Boolean networks. Phys. Rev. Lett. 108, 128702.
Griffiths, R.B., Wheeler, J.C., 1970. Critical points in multicomponent systems. Phys.
Rev. A 2, 1047–1064. http://dx.doi.org/10.1103/PhysRevA.2.1047.
Gutowitz, H., Langton, C., 1995. Mean field theory of the edge of chaos. In: Morán, F.,
Moreno, A., Merelo, J.J., Chacón, P. (Eds.), ECAL’95: Third European Conference
on Artificial Life. Springer-Verlag, Heidelberg, pp. 52–64.
Hanel, R., Pöchacker, M., Thurner, S., 2010. Living on the edge of chaos: Minimally
nonlinear models of genetic regulatory dynamics. Phil. Trans. R. Soc. A 368,
5583–5596.
Hochstetter, J., Zhu, R., Loeffler, A., Diaz-Alvarez, A., Nakayama, T., Kuncic, Z., 2021.
Avalanches and edge-of-chaos learning in neuromorphic nanowire networks. Nature
Commun. 12, 1–13.
Holland, J.H., 1975. Adaption in Natural and Artificial Systems. The University of
Michigan Press, Ann Arbor, MI.
Hooke, R., 1665. Micrographia, or, Some Physiological Descriptions of Minute Bodies
Made by Magnifying Glasses: With Observations and Inquiries Thereupon. The
Royal Society, London, UK.
Ishii, M., J.G., Teuscher, C., 2019. On the sparse percolation of damage in finite non-
synchronous random boolean networks. Physica D 398, 84–91. http://dx.doi.org/
10.1016/j.physd.2019.05.011.
Ito, K., Gunji, Y.P., 1994. Self-organisation of living systems towards criticality at the
edge of chaos. Biosystems 33, 17–24.
Jacobs, W.M., Frenkel, D., 2017. Phase transitions in biological systems with many
components. Biophys. J. 112, 683–691.
Jaeger, H., 2001. The Echo State Approach to Analysing and Training Recurrent
Neural Networks. Technical Report GMD Report 148, GMD-Forschungszentrum
Informationstechnik.
Kaneko, K., Suzuki, J., 1994. Evolution to the edge of chaos in an imitation game. In:
Langton, C.G. (Ed.), Artificial Life III: Proceedings of the Workshop on Artificial
Life. Addison-Wesley Longman Publishing Co. Boston, MA, pp. 43–54.
Kauffman, S.A., 1969. Metabolic stability and epigenesis in randomly constructed ge-
netic nets. J. Theor. Biol. 22, 437–467. http://dx.doi.org/10.1016/0022-5193(69)
90015-0.
Kauffman, S.A., 1993. The Origins of Order: Self-Organization and Selection in
Evolution. Oxford University Press, USA.
Krebs, H.A., Johnson, W.A., 1937. Metabolism of ketonic acids in animal tissues.
Biochem. J. 31, 645–660.
Langton, C.G., 1986. Studying artificial life with cellular automata. Physica D 22,
120–149. http://dx.doi.org/10.1016/0167-2789(86)90237-X.
Langton, C.G., 1990. Computation at the edge of chaos: Phase transitions and emergent
computation. Physica D 42, 12–37.
Legenstein, R., Maass, W., 2007. Edge of chaos and prediction of computational
performance for neural circuit models. Neural Netw. 20, 323–334.
Liberman, E.A., 1972. The cell as a molecular computer. Biofizika 17, 932–943.
Liberman, E.A., 1979. Analog-digital molecular cell computer. BioSystems 11, 111–124.
Liberman, E.A., Minina, S.V., 1996. Cell molecular computers and biological
information as the foundation of nature’s laws. BioSystems 38, 173–177.
Lilak, S., Woods, W., Scharnhorst, K., Dunham, C., Teuscher, C., Stieg, A., Gimzewski, J.,
2021. Spoken digit classification by in-materio reservoir computing with neuromor-
phic atomic switch networks. Front. Nanotechnol. 3, 675792. http://dx.doi.org/10.
3389/fnano.2021.675792.
Liu, M., Bassler, K.E., 2006. Emergent criticality from co-evolution in random Boolean
networks. Phys. Rev. E 74, 041910.
Lu, Q., Teuscher, C., 2014. Damage spreading in spatial and small-world random
Boolean networks. Phys. Rev. E 89, 022806. http://dx.doi.org/10.1103/PhysRevE.
89.022806.
Luque, B., Solé, R., 1997. Phase transitions in random networks: Simple analytic
determination of critical points. Phys. Rev. E 55, 257–260.
Luque, B., Solé, R.V., 2000. Lyapunov exponents in random boolean networks. Phys. A:
Stat. Mech. Appl. 284, 33–45. http://dx.doi.org/10.1016/S0378-4371(00)00184-9.
Maass, W., Natschläger, T., Markram, H., 2002. Real-time computing without stable
states: A new framework for neural computation based on perturbations. Neural
Comput. 14, 2531–2560. http://dx.doi.org/10.1162/089976602760407955.
McCorduck, P., 2007. Th Edge of Chaos: A Novel. Sunstone Press, Santa Fe, NM.
Melby, P., Kaidel, J., Weber, N., Hübler, A., 2000. Adaptation to the edge of chaos in
the self-adjusting logistic map. Phys. Rev. Lett. 84, 5991–5993. http://dx.doi.org/
10.1103/PhysRevLett.84.5991.
Mitchell, M., Crutchfield, J.P., Hraber, P.T., 1994. Dynamics, computation, and the edge
of chaos: A re-examination. In: Cowan, G., Pines, D., Melzner, D. (Eds.), Complexity:
Metaphors, Models, and Reality. Addison-Wesley, Reading, MA, p. 497.
Mitchell, M., Hraber, P.T., Crutchfield, J.P., 1993. Revisiting the edge of chaos: Evolving
cellular automata to perform computations. Complex Syst. 7, 89–130.
Mora, T., Bialek, W., 2011. Are biological systems poised at criticality? J. Stat. Phys.
144, 268–302.
Moyo, D., 2018. Edge of Chaos: Why Democracy Is Failing To Deliver Economic
Growth-and how to Fix It. Basic Books, New York, NY.
Nakajima, M., Tanaka, K., Hashimoto, T., 2021. Scalable reservoir computing on
coherent linear photonic processor. Commun. Phys. 4, 1–12.
Nykter, M., Price, N.D., Aldana, M., Ramsey, S.A., Kauffman, S.A., Hood, L.E., Yli-
Harja, O., Shmulevich, I., 2008. Gene expression dynamics in the macrophage
exhibit criticality. Proc. Natl. Acad. Sci. 105, 1897–1900. http://dx.doi.org/10.
1073/pnas.0711525105.
Oswald, A., Köhler, J., Schmitt, R., 2018. Project Management at the Edge of Chaos.
Soringer-Verlag, Berlin, Heidelberg.
Packard, N.H., 1988. Dynamic Patterns in Complex Systems. World Scientific,
Singapore, pp. 29–301, Chapter Adaptation Toward the Edge of Chaos.
Pierre, D., Hübler, A., 1994. A theory for adaptation and competition applied to
logistic map dynamics. Physica D 75, 343–360. http://dx.doi.org/10.1016/0167-
2789(94)90292-5.
Rämö, P., Kesseli, J., Yli-Harja, O., 2006. Perturbation avalanches and criticality in gene
regulatory networks. J. Theoret. Biol. 242, 164–170. http://dx.doi.org/10.1016/j.
jtbi.2006.02.011.
Rohlf, T., Bornholdt, S., 2002. Criticality in random threshold networks: Annealed
approximation and beyond. Physica A 310, 245–259.
Rohlf, T., Gulbahce, N., Teuscher, C., 2007. Damage spreading and criticality in finite
random dynamical networks. Phys. Rev. Lett. 99, 248701.
Samuelsson, B., Socolar, J.E.S., 2006. Exhaustive percolation on random networks. Phys.
Rev. E 74, 036113.
Samuelsson, B., Troein, C., 2003. Superpolynomial growth in the number of attractors
in Kauffman networks. Phys. Rev. Lett. 90, 098701.
Shmulevich, I., Kauffman, S.A., Aldana, M., 2005. Eukaryotic cells are dynamically
ordered or critical but not chaotic. Proc. Natl. Acad. Sci. 102, 13439–13444.
Sipper, M., 1997. Evolution of Parallel Cellular Machines: The Cellular Programming
Approach. Springer-Verlag, Heidelberg.
Slavova, A., Ignatov, V., 2022. Edge of chaos in memristor cellular nonlinear networks.
Mathematics 10, 1288.
Snyder, D., Goudarzi, A., Teuscher, C., 2013. Computational capabilities of random
automata networks for reservoir computing. Phys. Rev. E 87, 042808. http://dx.
doi.org/10.1103/PhysRevE.87.042808.
Solé, R., Luque, B., 1995. Phase transitions and antichaos in generalized Kauffman
networks. Phys. Lett. A 196, 331–334.
Solé, R.V., Manrubia, S.C., Luque, B., Delgado, J., Bascompte, J., 1996. Phase transitions
and complex systems: Simple, nonlinear models capture complex systems at the
edge of chaos. Complexity 1, 13–26. http://dx.doi.org/10.1002/cplx.6130010405.
Suzuki, J., Kaneko, K., 1994. Imitation games. Physica D 75, 328–342.
Toffoli, T., Margolus, N., 1987. Cellular Automata Machines. MIT Press, Cambridge,
MA.
Torres-Sosa, C., Huang, S., Aldana, M., 2012. Criticality is an emergent property
of genetic networks that exhibit evolvability. PLoS Comput. Biol. 8, 1–18. http:
//dx.doi.org/10.1371/journal.pcbi.1002669.
Tran, D.J., Teuscher, C., 2021. Computational capacity of complex memcapaci-
tive networks. J. Emerg. Technol. Comput. Syst. 17, http://dx.doi.org/10.1145/
3445795.
Turing, A.M., 1936–1937. On computable numbers, with an application to the entschei-
dungsproblem. In: Proceedings of the London Mathematical Society. pp. 230–265.
1937. Corrections Proc. London Math. Soc. 43, 544–546.
Turing, A.M., 1952. The chemical basis of morphogenesis. Philos. Trans. R. Soc. London
B 237, 37–72.
Turing, A.M., 1969. Intelligent machinery. In: Meltzer, B., Michie, D. (Eds.), Machine
Intelligence, Vol. 5. Edinburgh University Press, Edinburgh, pp. 3–23.
Ulanowicz, R.E., 2002. The balance between adaptability and adaptation. BioSystems
64, 13–22.
Wikipedia, 2022. Edge of chaos — Wikipedia, the free encyclopedia. http:
//en.wikipedia.org/w/index.php?title=Edge%20of%20chaos&oldid=1066177550.
[Online; Accessed 31 January 2022].
Wolfram, S., 1984. Universality and complexity in cellular automata. Physica D 10,
1–35.
Zeigler, B.P., 2002. The brain-machine disanalogy revisited. BioSystems 64, 127–140.


（参考文献可上下滑动查看）



复杂科学最新论文


集智斑图顶刊论文速递栏目上线以来，持续收录来自Nature、Science等顶刊的最新论文，追踪复杂系统、网络科学、计算社会科学等领域的前沿进展。现在正式推出订阅功能，每周通过微信服务号「我的集智」推送论文信息。扫描下方二维码即可一键订阅：




推荐阅读



点击“阅读原文”，追踪复杂科学顶刊论文