关键词:强关联系统,张量网络,相变,层间耦合,三维海森堡模型,涌现
论文题目:Efficient Tensor Network Algorithm for Layered Systems
论文来源:Physical Review Letters
论文链接:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.130.130601
理解强关联系统中的涌现现象在现代物理学中具有重要意义。研究这些系统的最强大的工具是张量网络方法,三维张量网络算法由于其较高的复杂性而更具挑战性。
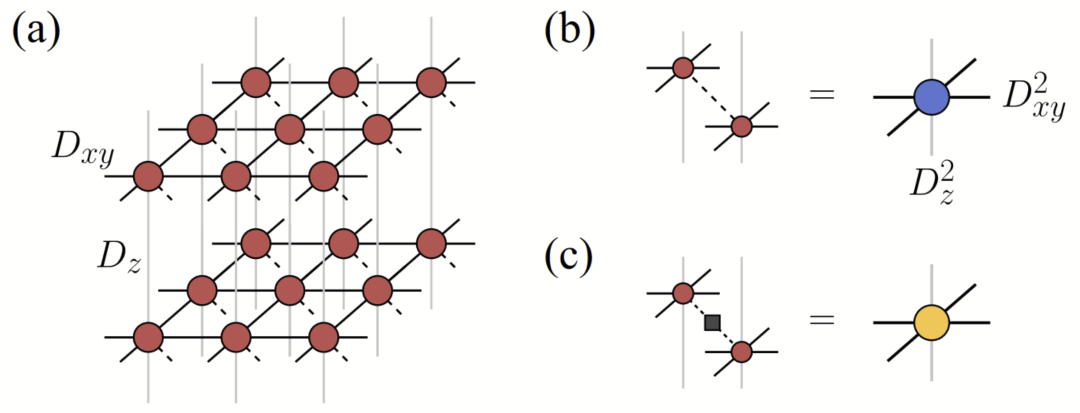
受张量网络在一维和二维系统中巨大成功的启发,这项最新发表于 Physical Review Letters 的研究,介绍了一种基于无限投影纠缠对态(entangled-pair states)的高效张量网络方法来处理分层二维系统。从各向异性三维无限投影纠缠对态假设出发,论文提出了一个收缩方案,在该方案中弱相互作用层被有效地从层的中心解耦,以便可以使用二维收缩方法高效地进行收缩,同时保持层的中心连接,以捕捉最相关的层间关联。
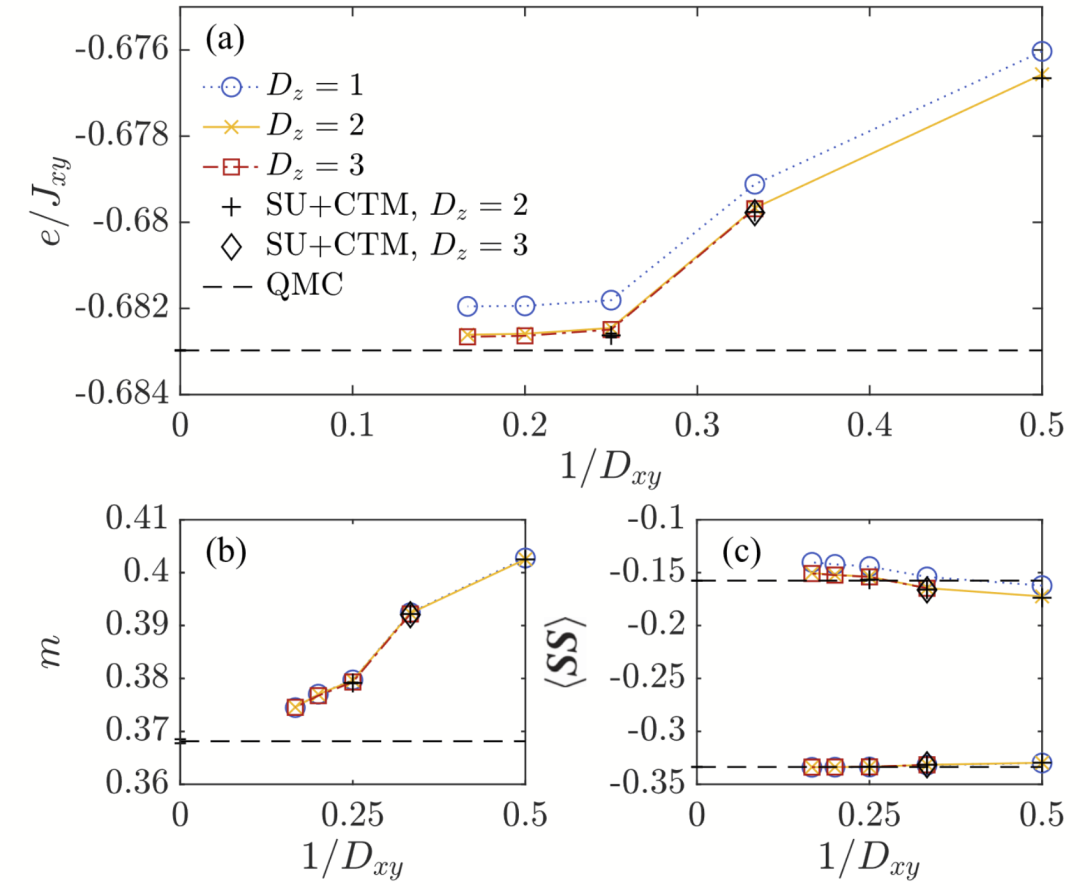
作者展示了立方晶格上各向异性三维海森堡模型的基准数据,这些数据与量子蒙特卡罗和完整三维收缩结果非常接近。最后,作者还研究了 Shastry-Sutherland 模型中带有层间耦合的二聚体的 Néel 相变(Néel phase transition)过程,这是一个由于负符号问题而难以通过量子蒙特卡罗求解的阻挫自旋模型。
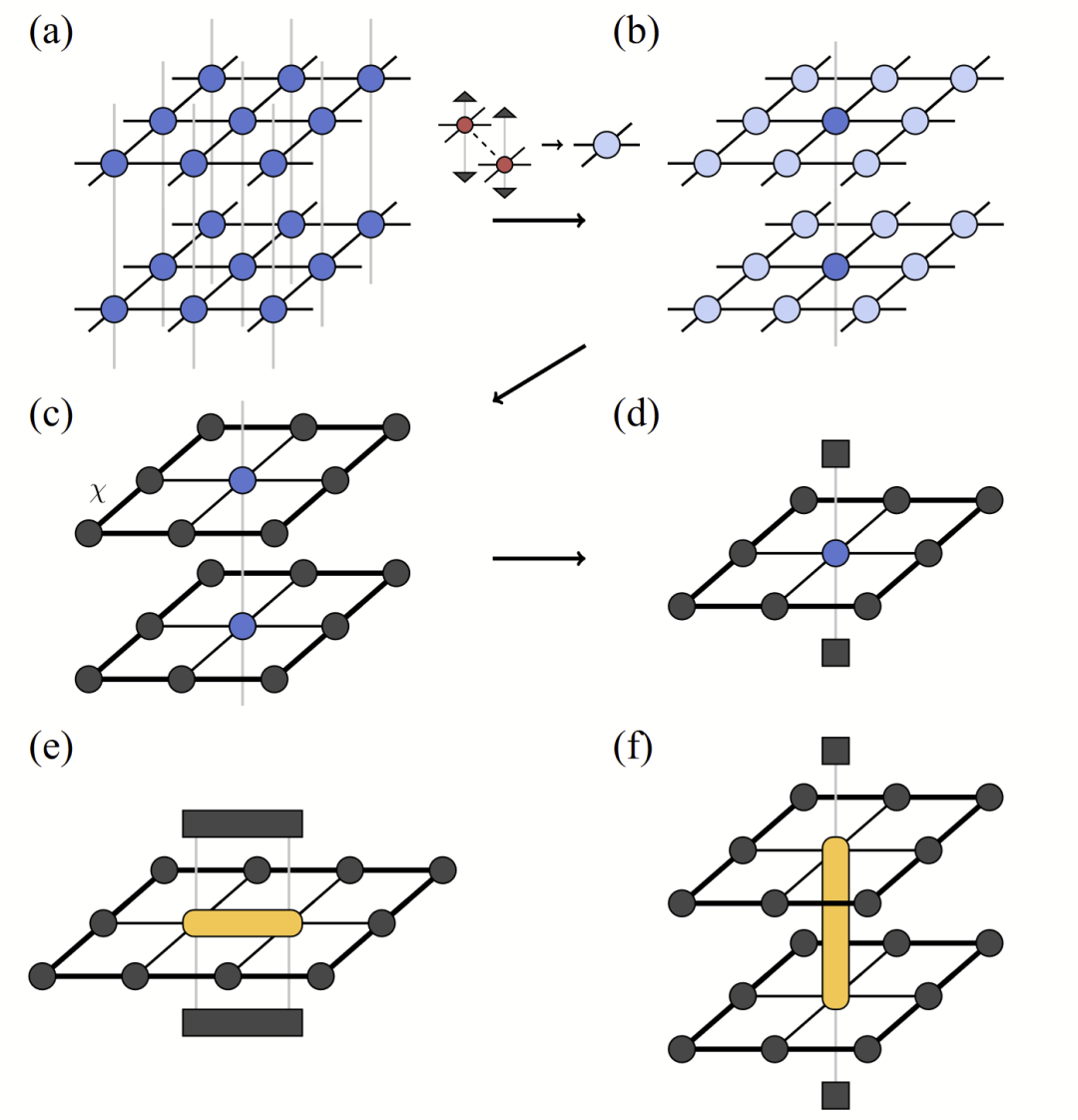
图2. 论文提出的分层转角矩阵收缩法(layered corner transfer matrix, LCTM)的主要步骤。
推荐阅读