自旋玻璃是具有随机相互作用的无序磁铁,找到自旋玻璃基态对理解许多物理系统的性质,以及解决跨多学科的组合优化问题都很有帮助。但经过几十年努力,仍然缺乏一种同时满足高精度和高效率的算法。近日国防科技大学范长俊等人发表在 Nature Communications 上的新研究介绍了一种深度强化学习框架 DIRAC,可以仅在小规模的自旋玻璃实例上进行训练,然后应用于任意规模的实例上。该框架有助于更好地理解低温自旋玻璃的性质,其采用的规范变换技术在物理学和人工智能之间建立了深刻的联系,此外,也为强化学习在巨大的构型空间中探索开辟了一条充满希望的道路。
为了探讨图神经网络在算法神经化求解的发展与现实应用,集智俱乐部联合国防科技大学系统工程学院副教授范长俊、中国人民大学高瓴人工智能学院助理教授黄文炳,共同发起「图神经网络与组合优化」读书会,聚焦神经算法推理、组合优化问题求解、几何图神经网络,以及算法神经化求解在 AI for Science 中的应用等方面。读书会从6月14日开始,持续时间预计8周。欢迎感兴趣的朋友报名参与,详情见文末。
关键词:自旋玻璃,深度强化学习,组合优化,统计物理,规范变换
张澳 | 作者
范长俊 | 审校
梁金 | 编辑

Searching for spin glass ground states through deep reinforcement learning
https://www.nature.com/articles/s41467-023-36363-w
自旋玻璃是具有随机相互作用的无序磁铁,通常相互冲突。找到自旋玻璃的基态不仅对于理解无序磁体和许多其他物理系统的性质至关重要,而且对于解决跨多学科的组合优化问题也很有用。但经过几十年的努力,仍然缺乏一种同时满足高精度和高效率的算法。
近日国防科技大学范长俊等人发表在 Nature Communications 上的研究介绍了一个深度强化学习框架——DIRAC(Deep reinforcement learning for spIn-glass gRound-stAte Calculation),它可以仅在小规模的自旋玻璃实例上进行训练,然后应用于任意规模的实例上。相比于其它方法,DIRAC 显示出更好的可扩展性(scalability),可以用来增强任何热退火方法。对2D、3D 和4D Edwards-Anderson自旋玻璃实例的广泛计算表明,DIRAC 的性能优于现有的方法。
该框架将有助于我们更好地理解低温自旋玻璃相的性质,这是统计物理学中的一个基本挑战。此外,DIRAC中采用的规范变换技术在物理学和人工智能之间建立了深刻的联系。特别是,这为强化学习模型在巨大的构型空间中探索开辟了一条充满希望的道路,这非常有助于解决许多组合优化难题。
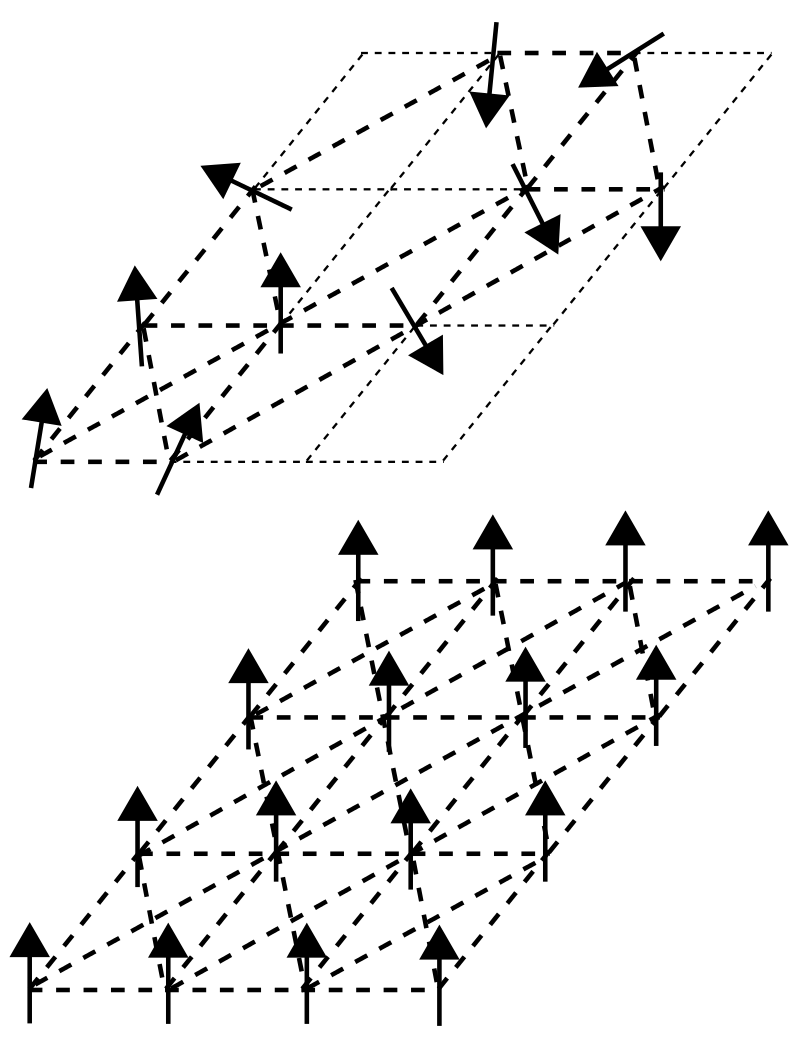
伊辛自旋玻璃是一种经典的无序系统,已经被研究了几十年。它奇特的行为引起了数学、计算机科学和生物学的极大兴趣。自旋玻璃中内生的淬致无序(quenched disorder,指决定系统行为的参数为不随时间演变的随机变量)使得系统的基态难以搜索,这种现象也被称为阻挫(frustration,即自旋的取向难以满足局部能量最低的要求)。
图1.自旋玻璃的随机自旋结构(上)和铁磁体的有序结构(下) | 来源:维基百科
然而搜索自旋玻璃基态是个关键问题,目前至少有三个解决该问题的强烈动机:
(1)该问题是揭开自旋玻璃奇怪而复杂行为的关键,特别是在不同边界条件下的基态能量可以用来计算自旋玻璃的刚度指数,从而确保有限温度下自旋玻璃相的存在;
(2)该问题有助于解决许多组合优化难题,因为这些难题中都存在自旋玻璃的形式;
(3)该问题有助于神经网络优化工具的开发,有关自旋玻璃及其基态的研究推动了空腔法(cavity method)和置信传播(Belief Propagation)等优化工具的发展,并将进一步推动计算复杂性理论。
在三维或更高维中搜索自旋玻璃基态是 NP 难题,精确的分枝定界法(branch-and-bound approach,将优化问题分解成更小的子问题并使用边界函数来消除不能包含最优解的子问题)只能用于非常小的系统,因此我们对于较大规模、较一般的系统缺乏一种既具有高精度又具有高效率的方法。
过去常常依靠启发式方法,特别是基于热退火的蒙特卡罗方法,如模拟退火(SA,simulated annealing)、群体退火和并行退火(PT,parallel tempering),这些方法已经在统计物理学中得到了很好的研究。最近,许多研究证明强化学习(RL,reinforcement learning)是解决许多组合优化问题的有效工具。与传统方法相比,基于强化学习的方法在精度和效率间取得了更好的平衡。当前已有用于搜索二维自旋玻璃系统基态的强化学习算法,但该算法无法找到三维或更高维度自旋玻璃系统的基态。本文介绍的 DIRAC 框架可以直接计算自旋玻璃的基态,具有精度高、可扩展性强,适用于任何热退火算法等优点。
与许多解决组合优化问题的强化学习框架类似,DIRAC 框架将自旋玻璃基态搜索视为马尔可夫决策过程(Markov decision process,MDP),即主体与环境相互作用并学习能积累最大收益的最优策略,根据该策略依次采取长远的行动。为了更好地描述这一过程,首先在伊辛自旋玻璃基态计算的背景下定义了状态、行动和奖励。
状态:状态s代表观察到的自旋玻璃实例,包括自旋构型σi和耦合强度Jij,在此基础上将选择最佳行动。当主体将每个自旋翻转一次后,达成终态ST 。
行动:行动a(i)意味着翻转自旋i 。
奖励:奖励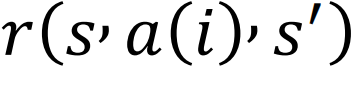 定义为将自旋i从状态s翻转到一个新的状态s’之后的能量变化。
该研究试图通过强化学习框架,学习一个最优策略,它接受任意观测状态s,并产生最大化未来累计收益的自旋翻转行为a(i)。该框架能否成功主要取决于以下两个关键问题:(1)如何有效地表征状态和行动?(2)如何利用这些表征来计算 Q 值(Q-value,用于预测在一种状态下某个行动的长期收益)。作者们将这两个问题分别称为编码问题(encoding problem)和解码问题(decoding problem)。该框架所学习的策略也就是一组编码参数和解码参数
定义为将自旋i从状态s翻转到一个新的状态s’之后的能量变化。
该研究试图通过强化学习框架,学习一个最优策略,它接受任意观测状态s,并产生最大化未来累计收益的自旋翻转行为a(i)。该框架能否成功主要取决于以下两个关键问题:(1)如何有效地表征状态和行动?(2)如何利用这些表征来计算 Q 值(Q-value,用于预测在一种状态下某个行动的长期收益)。作者们将这两个问题分别称为编码问题(encoding problem)和解码问题(decoding problem)。该框架所学习的策略也就是一组编码参数和解码参数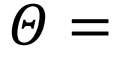
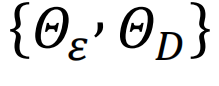 。
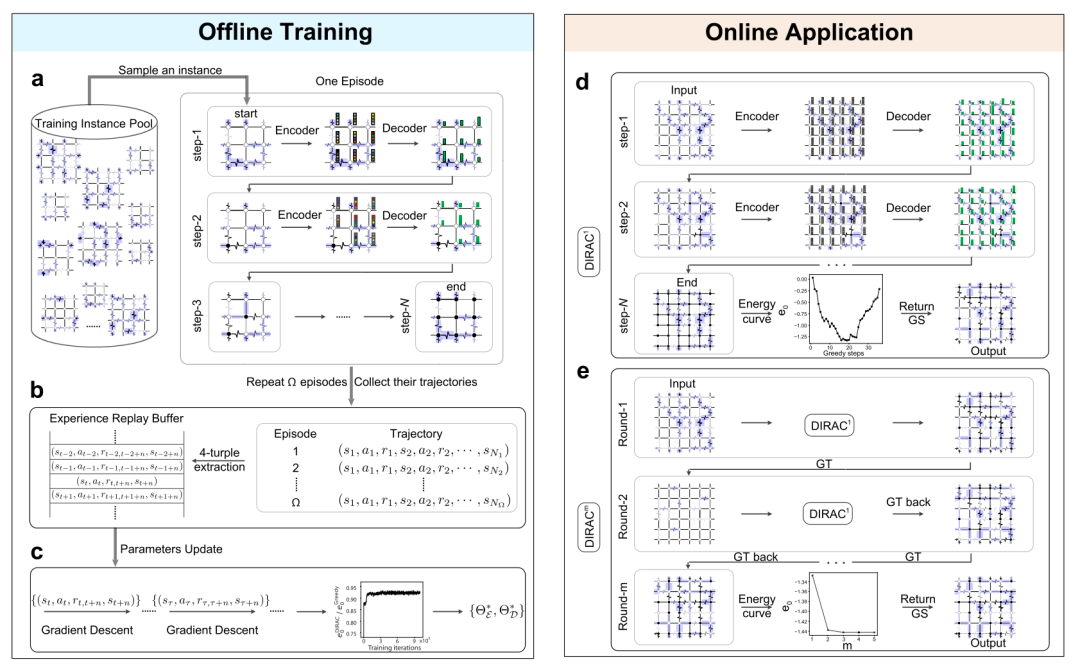
DIRAC 具体过程如图 1 所示,包括两个阶段:离线训练和在线应用。离线训练中,DIRAC 主体自学随机生成的小规模 EA 自旋玻璃(Edwards-Anderson spin glass)实例。对于每个实例,主体通过一系列的状态、行动和奖励与环境进行交互(图2-a)。同时,该主体获得了更新其参数的经验,从而提高了搜索 EA 自旋玻璃基态的能力(图2-b,c)。在线应用中,训练好的 DIRAC 主体可以应用于比训练规模大得多的 EA 自旋玻璃实例,可以直接应用(DIRAC1,图2-d),可以迭代应用(DIRACm,图2-e),也可以嵌入热退火方法中应用(DIRAC-SA 和 DIRAC-PT)。
图2. DIRAC 框架概述。该框架由两阶段组成:离线训练和在线应用。
(左图)训练过程,先随机生成小规模 EA 自旋玻璃实例作为训练数据,其耦合强度从高斯分布中采样。(a)对于每个episode,主体由自旋全部向上的构型(configuration)开始,至自旋全部向下的构型为止,每个自旋只翻转一次。对下一个episode,重新采样训练实例。为了确定应该采取的正确行动,DIRAC 首先将每个节点编码为嵌入向量(图中表示为颜色条),然后为每个预测长期收益的节点解码 Q 值(图中表示为高度与值成正比的绿色条)。(b)当一个episode结束后,收集过程轨迹,提取四元组转换(4-turple transitions),并将其推入缓冲区(experience replay buffer,保留Sbuffer最近N步转换的队列)。(c)为更新参数
。
DIRAC 具体过程如图 1 所示,包括两个阶段:离线训练和在线应用。离线训练中,DIRAC 主体自学随机生成的小规模 EA 自旋玻璃(Edwards-Anderson spin glass)实例。对于每个实例,主体通过一系列的状态、行动和奖励与环境进行交互(图2-a)。同时,该主体获得了更新其参数的经验,从而提高了搜索 EA 自旋玻璃基态的能力(图2-b,c)。在线应用中,训练好的 DIRAC 主体可以应用于比训练规模大得多的 EA 自旋玻璃实例,可以直接应用(DIRAC1,图2-d),可以迭代应用(DIRACm,图2-e),也可以嵌入热退火方法中应用(DIRAC-SA 和 DIRAC-PT)。
图2. DIRAC 框架概述。该框架由两阶段组成:离线训练和在线应用。
(左图)训练过程,先随机生成小规模 EA 自旋玻璃实例作为训练数据,其耦合强度从高斯分布中采样。(a)对于每个episode,主体由自旋全部向上的构型(configuration)开始,至自旋全部向下的构型为止,每个自旋只翻转一次。对下一个episode,重新采样训练实例。为了确定应该采取的正确行动,DIRAC 首先将每个节点编码为嵌入向量(图中表示为颜色条),然后为每个预测长期收益的节点解码 Q 值(图中表示为高度与值成正比的绿色条)。(b)当一个episode结束后,收集过程轨迹,提取四元组转换(4-turple transitions),并将其推入缓冲区(experience replay buffer,保留Sbuffer最近N步转换的队列)。(c)为更新参数 ,从缓冲区随机采样小批量转换,并依据相应公式梯度下降,重复该过程直至Ω=106。选取表现最好的模型作为最优模型。
(右图)应用时有两种策略:DIRAC1 和 DIRACm。(d)对于一个输入实例,DIRAC1 初始构型 {σi=+1},贪婪反转最高Q值的自旋直到{σi=-1}。将该过程出现的最低能量的构型返回为预测基态。(e)DIRACm 指由规范变换(gauge trnsformation,GT)连接的 DIRAC1 的m次迭代的顺序运行。对于每次迭代,规范变换将上次迭代的最低能量构型转换为 DIRAC1 的{σi=+1},并将其转换回当前迭代的输出。
,从缓冲区随机采样小批量转换,并依据相应公式梯度下降,重复该过程直至Ω=106。选取表现最好的模型作为最优模型。
(右图)应用时有两种策略:DIRAC1 和 DIRACm。(d)对于一个输入实例,DIRAC1 初始构型 {σi=+1},贪婪反转最高Q值的自旋直到{σi=-1}。将该过程出现的最低能量的构型返回为预测基态。(e)DIRACm 指由规范变换(gauge trnsformation,GT)连接的 DIRAC1 的m次迭代的顺序运行。对于每次迭代,规范变换将上次迭代的最低能量构型转换为 DIRAC1 的{σi=+1},并将其转换回当前迭代的输出。
为比较 DIRAC 搜索自旋玻璃基态的能力,该研究评估了不同方法在小自旋玻璃系统上的效果,结果表明 DIRAC 在基态搜索上表现优越(见图3a-c),并且其优异表现在不同大小的不同系统中均持续存在(见图3d-f)。
图3. 不同方法搜索基态的表现。为比较搜索精确基态的能力,研究者评估了不同方法在小自旋玻璃系统上的效果。对于小自旋玻璃系统,可以用分枝定界法计算基态真值,以此作为比较基准。(a-c)所选取的比较指标为搜索到基态的概率(记为P0),以1000次随机实例中搜索到基态的比例计算。将P0绘制为不同初始构型数量(ninitial)的函数。(d-f)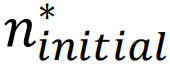 指P0为 1 时ninitial的最小值。
指P0为 1 时ninitial的最小值。
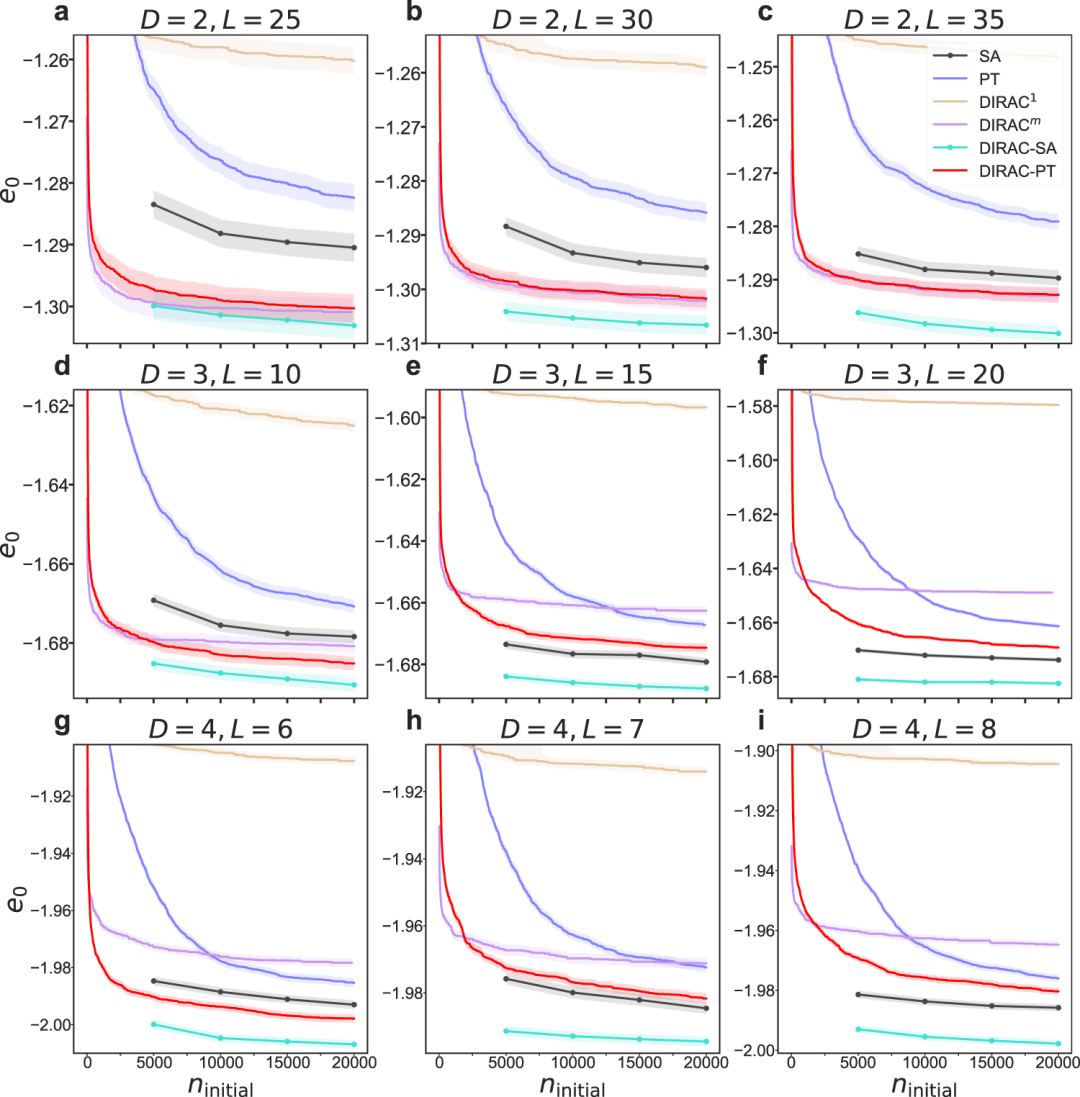
对于较大的系统,很难计算算法找到基态的概率,因为需要确认计算的“基态”是否是精确求解器获得的真正的基态,然而即使是最好的分枝定界求解器,也不能在可接受的时间内计算非常大的实例的基态。在这种情况下,对各种算法进行基准测试的一个更实际的选择,是比较它们预测的“基态”能量,这不一定是真正的基态能量,而是每个算法为每个特定实例提供的最低能量。结果表明(见图4),嵌入DIRAC的模拟退火表现最好,而DIRAC能作为通用插件提升任何热退火算法。
图4. 不同方法在最小化能量上的表现。e0指每个自旋的无序平均“基态”能量,将e0绘制为初始构型数量的函数。
除了搜寻基态的有效性之外,DIRAC 还具有计算效率。并且时间复杂度分析和寻找基态的性能分析表明,DIRAC 显示出比其他方法更好的可扩展性。随后将 DIRAC 应用于一般 NP 难问题,具体所选问题为最大割问题(max-cut problem),该问题可作为伊辛自旋玻璃与 NP 难问题之间映射的典型例子。结果表明 DIRAC 始终优于其他竞争对手。
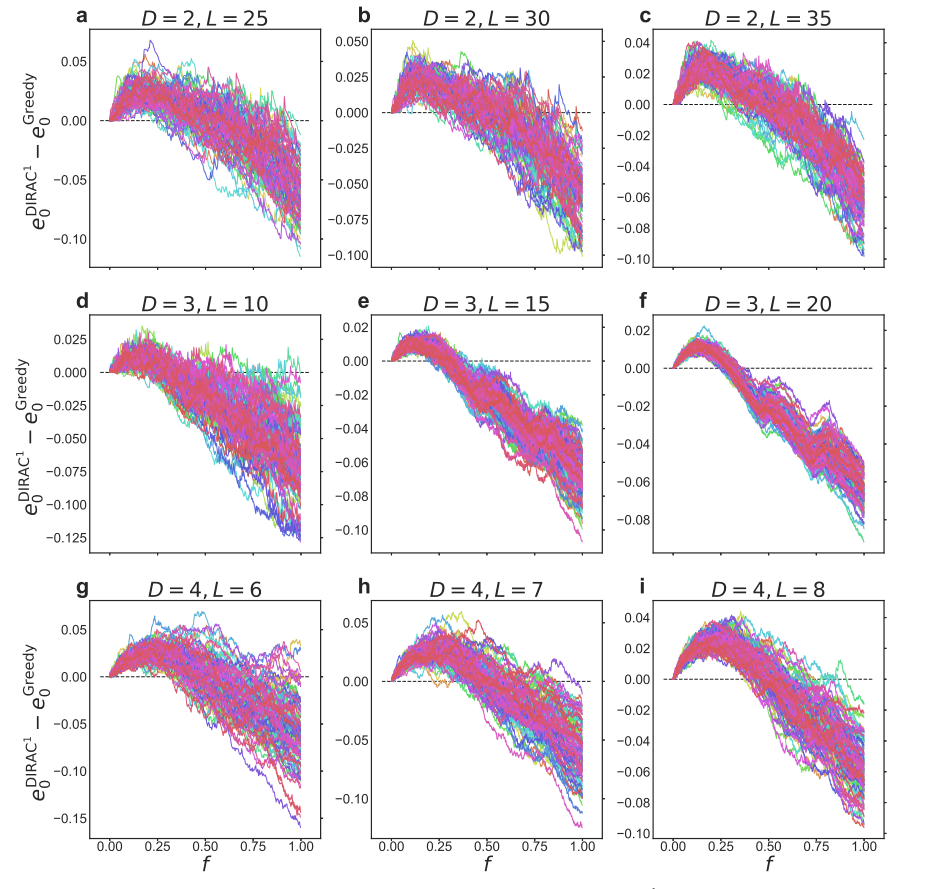
研究者尝试对 DIRAC 的优越性能提供了系统的解释。在图5中,比较了 DIRAC1 和贪婪算法在每个贪婪步骤中的系统能量差。结果表明,关注能量变化的贪婪算法代表了一种极其短视的策略,因为它只关注每一步的最大能量损失。图 5 清楚地表明,与这种目光短浅的策略相比,DIRAC1 在早期阶段总是暂时经历一个高能状态,以便在长期达到一个更低的能量状态。这一结果意味着 DIRAC 已经学会为长期收益做出短期牺牲。换句话说,DIRAC 已经被训练成要注意它的长期目标。
图5. 比较 DIRAC1 和贪婪算法(Greedy)每步的能量差,其中e0表示每个自旋的无序平均“基态”能量,f指已被翻转的自旋比例。可以看到在各系统中,与贪婪算法相比,DIRAC在早期阶段总是暂时经历高能状态,而在长期总能达到更低的能量状态。
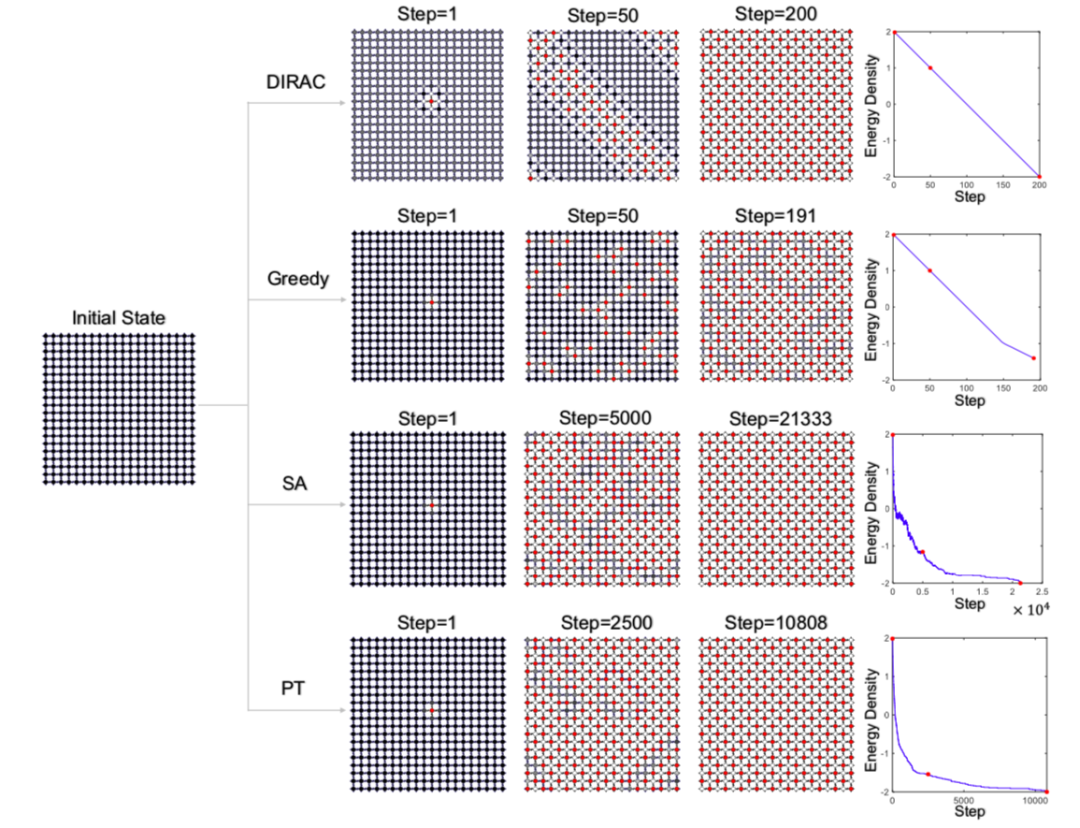
此外,在一个简单系统——反铁磁系统上,DIRAC有着传统方法无法比拟的优越表现。图6表明,DIRAC可以在不做任何错误尝试的情况下找到反铁磁系统的基态。这对于传统的基于局域探索的方法是不可能的:它们总是需要多次尝试来跳出局部极小值;从而找到基态所需的步数往往远大于系统节点个数。
图6. 在反铁磁系统上比较DIRAC与其他方法。该系统的基态为棋盘型结构。贪婪算法很快就陷入局部极小值;对于有着退火机制的模拟退火(Simulated Annealing)和并行退火(Parallel Tempering)而言,它们需要数万步的尝试才能到达基态。相对的,DIRAC只需200步就能达到系统基态,而这正是从初态出发到达基态理论上可能的最小步数。
在未来,深度图表示的进步可能使我们设计更好的编码器,强化学习技术的发展可能有助于更有效的训练。这两项技术都将进一步提高 DIRAC 在搜索伊辛自旋玻璃基态方面的性能。规范变换技术在 DIRAC 中的应用以及 DIRAC 与基于退火算法相结合的方法也可能对其他许多基于物理的人工智能研究有所启发,目前的框架仅仅是这一充满希望的冒险的开始。
范长俊,国防科技大学系统工程学院副教授,研究方向是人工智能与复杂系统。以第一作者或通讯作者在Nature Machine Intelligence、Nature Communications、AAAI 等顶级期刊和会议发表论文多篇。
现实世界中大量问题的解决依赖于算法的设计与求解。传统算法由人类专家设计,而随着人工智能技术不断发展,算法自动学习算法的案例日益增多,如以神经网络为代表的的人工智能算法,这是算法神经化求解的缘由。在算法神经化求解方向上,图神经网络是一个强有力的工具,能够充分利用图结构的特性,实现对高复杂度算法的高效近似求解。基于图神经网络的复杂系统优化与控制将会是大模型热潮之后新的未来方向。
为了探讨图神经网络在算法神经化求解的发展与现实应用,集智俱乐部联合国防科技大学系统工程学院副教授范长俊、中国人民大学高瓴人工智能学院助理教授黄文炳,共同发起「图神经网络与组合优化」读书会。读书会将聚焦于图神经网络与算法神经化求解的相关领域,包括神经算法推理、组合优化问题求解、几何图神经网络,以及算法神经化求解在 AI for Science 中的应用等方面,希望为参与者提供一个学术交流平台,激发参与者的学术兴趣,进一步推动相关领域的研究和应用发展。读书会从2023年6月14日开始,每周三晚 19:00-21:00 举行,持续时间预计8周。欢迎感兴趣的朋友报名参与!
详情请见:



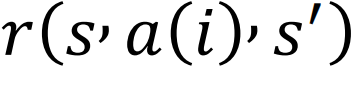 定义为将自旋i从状态s翻转到一个新的状态s’之后的能量变化。
定义为将自旋i从状态s翻转到一个新的状态s’之后的能量变化。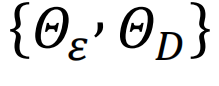 。
。
 ,从缓冲区随机采样小批量转换,并依据相应公式梯度下降,重复该过程直至Ω=106。选取表现最好的模型作为最优模型。
,从缓冲区随机采样小批量转换,并依据相应公式梯度下降,重复该过程直至Ω=106。选取表现最好的模型作为最优模型。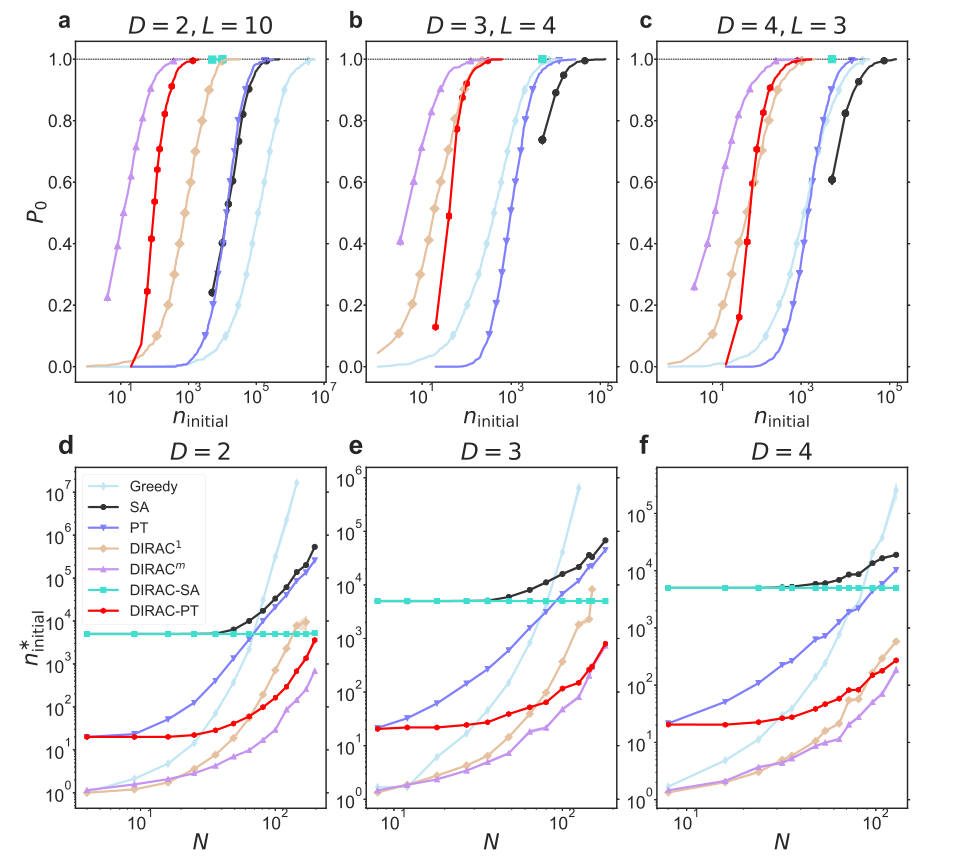
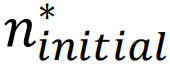 指P0为 1 时ninitial的最小值。
指P0为 1 时ninitial的最小值。